Тяговая характеристика автономного локомотива | Сила тяги и тяговые характеристики локомотивов

Подробности

Категория: Подвижной состав

• локомотив
• тяга

Содержание материала

• Сила тяги и тяговые характеристики локомотивов
• Сцепление ведущих колес локомотива с рельсами
• Физическая природа сцепления ведущих колес локомотива с рельсами
• Коэффициент сцепления и методы его оценки
• Тяговая характеристика автономного локомотива
• Тяговые свойства тепловозного дизеля
• Характеристики электрических передач тепловозов
• Построение тяговой характеристики тепловоза по характеристикам электродвигателей
• Опытные тяговые характеристики тепловозов с электрической передачей
• Опыт создания тепловозов с электрической передачей переменного тока
• Тяговые характеристики тепловозов с гидравлической передачей
• Опытные тяговые характеристики тепловозов с гидравлической передачей
• Тяговые характеристики тепловозов с механической передачей
• Характеристики тяговых электродвигателей постоянного тока
• Регулирование скорости движения и тяговые характеристики эпс постоянного тока
• Тяговые характеристики элекроподвижного состава постоянного тока
• Характеристики электроподвижного состава переменно-постоянного тока
• Тяговые свойства электровозов с бесколлекторными электродвигателями

Страница 5 из 18

Тяговая характеристика автономного локомотива и ее идеальная форма

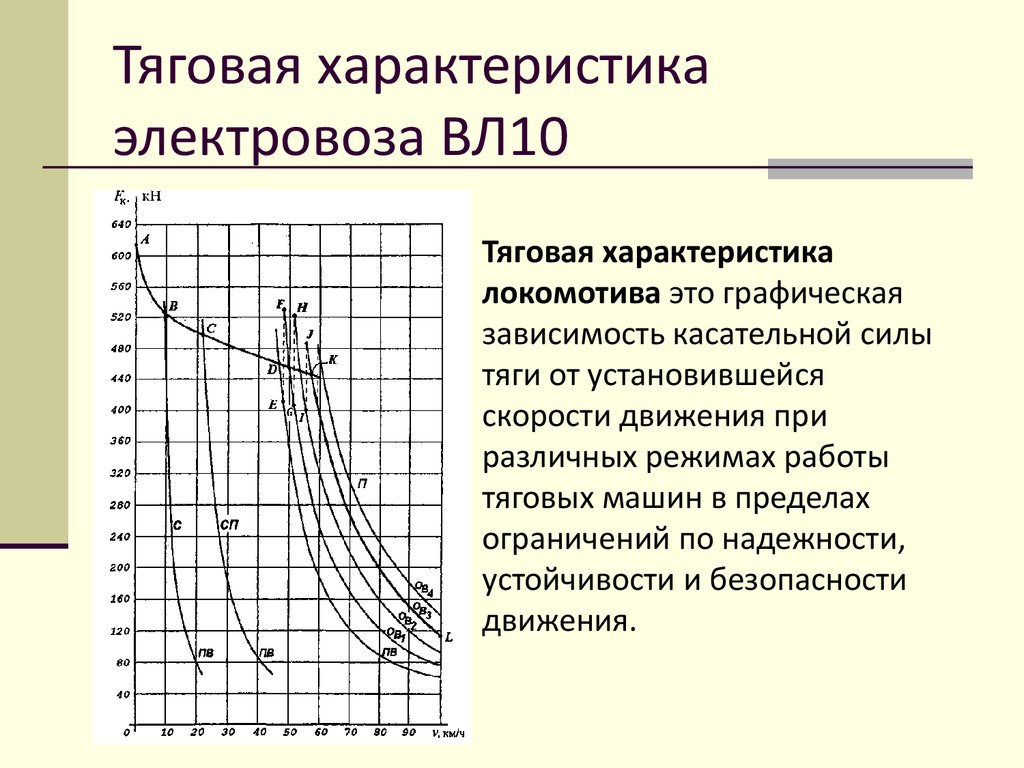
Тяговая характеристика локомотива — это зависимость силы тяги локомотива от скорости движения F=f(v) и режимов работы его энергетической установки, представленная графически.
Формально зависимости одной положительной величины — F oт другой — v и, следовательно, их графики могут быть различными, линейными или нелинейными.

Поэтому необходимо выяснить, какая форма зависимости наилучшим образом отвечает требованиям эффективного использования автономных локомотивов в эксплуатации.

Рис. 7. Возможные варианты формы тяговых характеристик

Рассмотрим несколько простейших возможных вариантов формы участка тяговой характеристики (рис. 7): линейное постепенное возрастание силы тяги в диапазоне скоростей движения от V1 до v2  —  по уравнению F=F1 + kv — отрезок 1-2; такое же линейное убывание силы тяги по уравнению F= F1 — kv  —  отрезок 1-3; и промежуточный вариант  — постоянство силы тяги F=F1 = const в том же диапазоне скоростей (линия 1-4).
Чтобы оценить степень пригодности той или иной формы, обратим внимание на величину необходимой мощности локомотивов с такими характеристиками.

Мощность N вообще, как работу А в единицу времени t, то есть N = A/t, можно при равномерном движении представить как N — FS/t = Fv — произведение силы на скорость.
Тогда, по первому варианту характеристики (линия 1-2 на рис. 7), если к > 0, мощность локомотива должна возрастать по мере увеличения скорости движения пропорционально квадрату ее приращения: N = N{+ к (у2~ v j )2, где TV) = F1 V1  —  мощность в исходной точке 1 (рис. 8, кривая 1-2).

По второму варианту (к < 0), если величина к невелика, то необходимая мощность может также даже несколько возрастать (за счет роста скорости) — кривая 1- 3 на рис. 8. При относительно больших значениях коэффициента к требуемая мощность локомотива может и уменьшаться с ростом скорости движения — кривая 1-3′.
И, наконец, для обеспечения постоянной величины силы тяги в рассматриваемом диапазоне скоростей движения (Fj = const) необходимая касательная мощность локомотива N должна возрастать прямо пропорционально скорости движения v, то есть: N- Fj v —  прямая 1-4 на рис. 8.

Рис. 8. Зависимости необходимой мощности локомотива от скорости движения при различных вариантах формы тяговой характеристики

Выше было показано, что мощность на колесах тепловоза (касательная), как и любого другого типа автономного локомотива (паровоза, газотурбовоза), прямо пропорциональна мощности его энергетической установки:

Величина номинальной (расчетной) мощности энергетической установки автономного локомотива ограничена ее свойствами. Тепловозные дизели не допускают перегрузки и, можно считать, что Ne макс=Ne ном — const. А раз наибольшая мощность источника энергии неизменна, то целесообразно к проектированию локомотива подходить так, чтобы эту величину мощности всегда (с соответствующими поправками) можно было бы реализовать на колесах. Иными словами, следует стремиться к тому, чтобы наибольшая возможная величина касательной мощности тепловоза так же могла быть использована при любой величине скорости движения, то есть чтобы соблюдалось аналогичное равенство NK макс=Νκ ном — const, что можно обеспечить при полном использовании мощности дизеля (считая, что произведение (1 -β)ηΠ6ρ мало зависит от скорости движения и может поэтому считаться неизменным) в рабочем диапазоне скоростей движения локомотива.

Тогда для автономного локомотива и для тепловоза, в частности, при выборе формы тяговой характеристики следует исходить из условия постоянства касательной мощности локомотива в рабочем диапазоне скоростей движения. Но, если принять условие NK = FKv=const, то для силы тяги получаем выражение FK=NK/v=const/v.
Условие FKv = const представляет собой уравнение гиперболы в координатах FK и v. Таким образом, если тяговая характеристика тепловоза F= f(v) будет иметь форму гиперболы (то есть если сила тяги обратно пропорциональна скорости  —  кривая 1-5 на рис. 7), касательная мощность локомотива будет постоянной при изменении скорости движения (см. рис. 8, прямая линия 1-5).

Такая зависимость касательной силы тяги от скорости и является идеальной формой тяговой характеристики автономного локомотива, источник энергии которого ограничен по мощности (рис. 9, а).
При такой форме характеристики на тепловозе теоретически обеспечивается возможность полного использования мощности дизеля в рабочем диапазоне скоростей движения. При проектировании тепловозов с различными типами передач конструкторам ставится задача обеспечить наиболее возможное приближение тяговой характеристики к идеальной гиперболической форме.

Рассмотрим подробней идеальную тяговую характеристику, показанную на рис. 9, а.

Рис. 9. Идеальная форма тяговой характеристики автономного локомотива: а  —  идеальная тяговая характеристика; б  —  зависимость тяговой (касательной) мощности локомотива от скорости движения при идеальной форме его тяговой характеристики

График гиперболы характерен тем, что кривая обеими ветвями (по осям координат) уходит в бесконечность, асимптотически приближаясь к осям координат (FK и v). Но бесконечных значений физических величин в технике, естественно, быть не может. Поэтому максимальные значения силы тяги и скорости движения ограничены.
Максимальная величина скорости движения локомотива vмакс ограничивается, как правило, по прочности его конструкции. Эта величина называется конструкционной скоростью локомотива vKOHCrp = vMaKC. Это ограничение показано на характеристике вертикальной чертой.

Максимальная величина сипы тяги, как уже рассматривалось выше, ограничивается основным законом локомотивной тяги.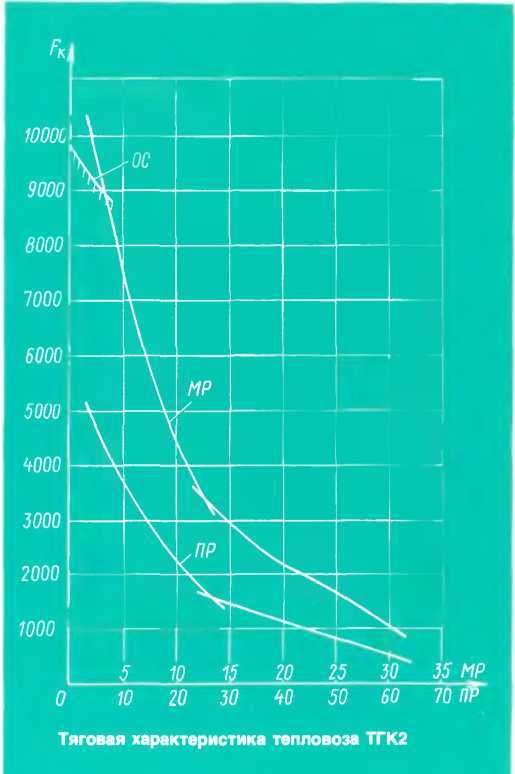 Это ограничение определяется значениями расчетного коэффициента сцепления. Максимальное значение допускаемой силы тяги имеет место при трогании локомотива с места. Ограничение по величине силы тяги по условиям сцепления также показано на характеристике своего рода границей (линия А В). Она не горизонтальна и снижается по мере роста скорости, так как уменьшается величина расчетного коэффициента сцепления (см. рис. 6).
Линия ограничения по сцеплению пересекается с гиперболической частью характеристики в точке В, которой соответствует величина скорости у’.Эту скорость, при которой происходит как бы перелом характеристики для паровозов, называли скоростью порога.

Таким образом, идеальная тяговая характеристика автономного локомотива состоит из двух частей: ограничение силы тяги по сцеплению АВ (диапазон скоростей от 0 до ν’) и участок гиперболы ВС —  ограничение сипы тяги по мощности энергетической установки (диапазон скоростей от ν’до vK0HCTp)·
Так как гиперболической является только часть характеристики, то условие постоянства касательной мощности локомотива обеспечивается в диапазоне скоростей движения v’ — vKOHCTp (рис. 9, б). Этот диапазон можно назвать рабочим для локомотива.

В диапазоне скоростей движения от 0 до v’ мощность энергетической установки локомотива из-за ограничения величины силы тяги по сцеплению полностью использована быть не может, а в самом начале координат (при у=0) она вообще равна нулю. Поэтому работа локомотива в этом диапазоне скоростей неэффективна и его следует считать нерабочим.
Фактически при проектировании локомотивов рабочий диапазон скоростей движения начинают при скорости v , которая несколько выше скорости ν’. Это дает некоторую гарантию (ввиду случайности величины коэффициента сцепления) реализации величины силы тяги FKp, которую принимают за расчетную силу тяги автономного локомотива. Скорость vp, соответствующую расчетному значению силы тяги FKp, называют расчетной скоростью (точнее, скоростью движения на расчетном подъеме).

Величины FKp и vp являются важнейшими техническими параметрами локомотивов, используемых в тяговых расчетах. Для отечественных магистральных локомотивов эти величины приводятся в Правилах тяговых расчетов.

• Назад
• Вперёд

• Назад
• Вперёд

Близкие публикации:

• Использование присадок к маслам на тепловозах
• Энергетика локомотивов
• Ремонт тягового генератора переменного тока тепловозов
• Ремонт тяговых генераторов постоянного тока тепловозов
• Организация текущего ремонта ТР-3 тяговых электродвигателей тепловозов

© 2009-2023 — lokomo.ru, железные дороги.

Тяговая характеристика локомотива

Чем
большую касательную силу тяги сможет
реализовать локомотив, тем большее
число вагонов он сможет переме­щать.
Максимальная сила тяги локомотива равна
сумме мак­симальных сил тяги движущих
колесных пар. По аналогии с формулой
(3.1) для всего локомотива

F_К
=
P_СЦ
ψ_К

(3.1)

где
P_СЦ—
сцепной вес локомотива;

ψ_К—
коэффициент сцепления локомотива.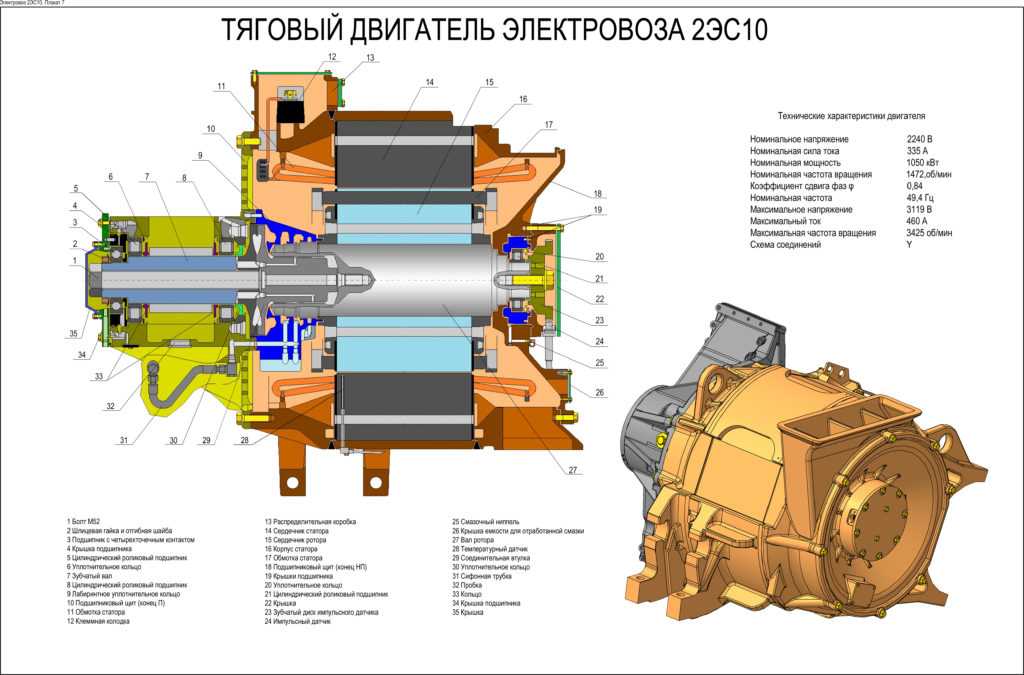

Сцепной
вес локомотива равен весу, приходящемуся
на движущие колесные пары, т. е. на такие,
к которым приложен вращающий момент. У
современных локомотивов все ко­лесные
пары выполняют движущими, и поэтому у
них сцеп­ной вес равен полному весу.

Коэффициент
сцепления локомотива представляет
собой коэффициент пропорциональности,
связывающий P_СЦ
и F_K.
По
величине ψ_К
всегда меньше ψ_О
ввиду того, что в общем случае колесные
пары локомотива работают в неодинаковых
условиях по следующим причинам:

1. невозможно
   добиться абсолютного равенства
   вертикаль­ных сил Р,
   действующих
   на отдельные колесные пары, и вра­щающих
   моментов М,
   приложенных
   к каждой из них;

2. условия
   сцепления у отдельных колесных пар,
   как пра­вило, разные.

Поэтому
при движении локомотива всегда имеется
по меньшей мере одна колесная пара, у
которой условия реализации силы тяги
будут худшими, чем у других колесных
пар, машинисту при этом приходится так
регулировать работу локомотива, чтобы
эта колесная пара (ее принято называть
лимитирующей) не буксовала. Очевидно,
что остальные колесные пары будут
реализовывать силы тяги меньше, чем воз
можно по условиям сцепления.

Для
всех локомотивов, эксплуатирующихся
на железных дорогах нашей страны, опытным
путем получены зависимости ψ_К

в функции скорости движения. В частности,
для тепловоза 2ТЭ10Л эта зависимость
имеет вид:

(3.2)

где
V
— скорость движения тепловоза, км/ч.

Максимальную
касательную силу тяги, ограниченную
сцеплением колес с рельсами обычно
обозначают F_СЦ.
По­этому с учетом (3.2) формула (3.1) для
тепловоза 2ТЭ10Л будет иметь вид:

(3.3)

Таким
образом, максимальная сила тяги локомотива
ограничена сцеплением колес с рельсами.
Зависимость силы F_сц
от
скорости движения локомотива называется
ограничением силы тяги по сцеплению
(рис. 3.1, кривая 1).

Рис.
3.1. Тяговая характеристика локомотива

Однако
максимальная касательная сила тяги
локомотива не может изменяться в
соответствии с кривой 1
во
всем рабо­чем диапазоне скоростей
движения локомотива.

Как
известно из физики, произведение силы
тяги на ско­рость движения есть
мощность. В соответствии с этим
каса­тельная мощность локомотива

N_K
= F_СЦ
V

(3.4)

Выполнив
соответствующие расчеты с использованием
фор­мул
(3.3) и (3.4), можно убедиться, что при
увеличении V
каса­тельная
мощность локомотива будет увеличиваться.
Однако в соответствии с законом сохранения
и преобразования энергии эта мощность
не может быть больше мощности дизеля у
теп­ловоза или суммарной мощности
тяговых электродвигателей у электровоза.

При
некоторой, вполне определенной для
каждого локомо­тива
скорости V_П
(см.
рис, 3.1), называемой скоростью порога,
мощность
N_К
определяемая
по (3.4),
становится равной мощности дизеля, а у
электровоза — мощности его тяговых
элект­родвигателей.

Начиная
с этой скорости, сила тяги локомотива
будет ог­раничена не сцеплением, а
мощностью, которая у тепловоза будет
равна мощности дизеля за вычетом
мощности, необхо­димой для обеспечения
действия ряда вспомогательных ме­ханизмов
и систем (о них будет рассказано ниже),
и потерь, неизбежных при преобразованиях
механической работы ди­зеля.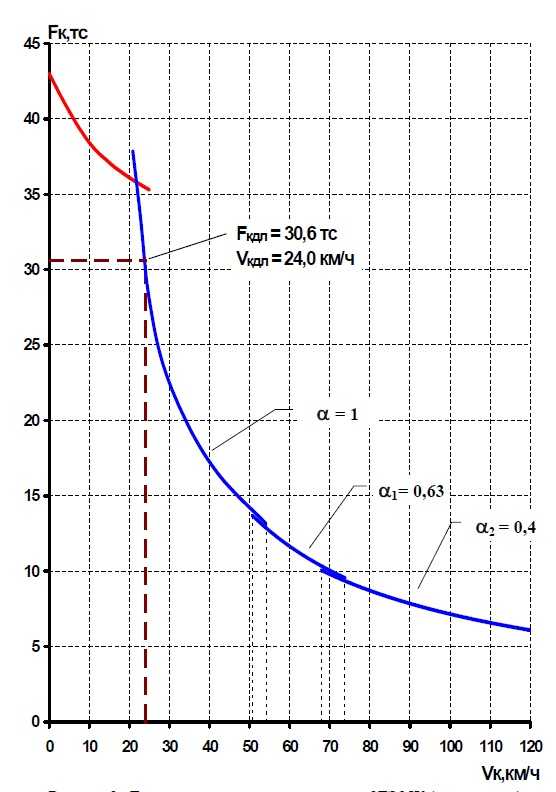 В
результате, начиная со скорости порога,
сила тяги ло­комотива будет изменяться
по линии 2,
которая
у тепловозов называется ограничением
по мощности дизеля.

Вследствие
этого при скорости
движения
тепловоза, рав­ной, например, V₁
(см. рис. 3.1), он будет развивать силу тяги
F_K1,
а не F_СЦ1|,
причем F_K1<
F_СЦ1.

Все
сказанное в полной мере относится и к
другим локо­мотивам.

Кроме
двух указанных ограничений, тяговая
характерис­тика каждого локомотива
имеет еще одно — по конструкци­онной
скорости движения V_К
(cm.
рис.
3.1). При движении ло­комотива с
конструкционной скоростью детали
привода ко­лесной нары, передающие
на нее вращающий момент, вра­щаются
с максимально допустимой частотой,
превышение ко­торой может привести
к их поломке.

Тяговая
характеристика локомотива, содержащая
ограни­чения
по сцеплению, мощности и конструкционной
скорости, называется
предельной тяговой характеристикой.
При работе по этой характеристике
локомотив полностью реализует свои
тяговые возможности.

Величина
касательной мощности, которая необходима
в данный момент времени, зависит от
многих факторов и в пер­вую очередь
от массы поезда. Очень часто машинисту
не нужно реализовывать максимальную
касательную мощность.

Поэтому
на каждом локомотиве предусматривается
воз­можность реализации нескольких
уменьшенных значений ка­сательной
мощности. Число этих промежуточных
значений у тепловозов
равно 7 — 15 (2).

Каждому
такому значению касательной мощности
соответствует своя зависимость силы
тяги F_K
от
скорости V
(см.
рис. 3.1, линии I
— IV).
Нужное в данный момент значение
ка­сательной мощности машинист задает
с помощью контролле­ра путем установки
его главной рукоятки в соответствующее
положение (позицию).

Позиции
главной рукоятки контроллера машиниста,
также как
и соответствующие им тяговые характеристики,
обозна­чают
цифрами.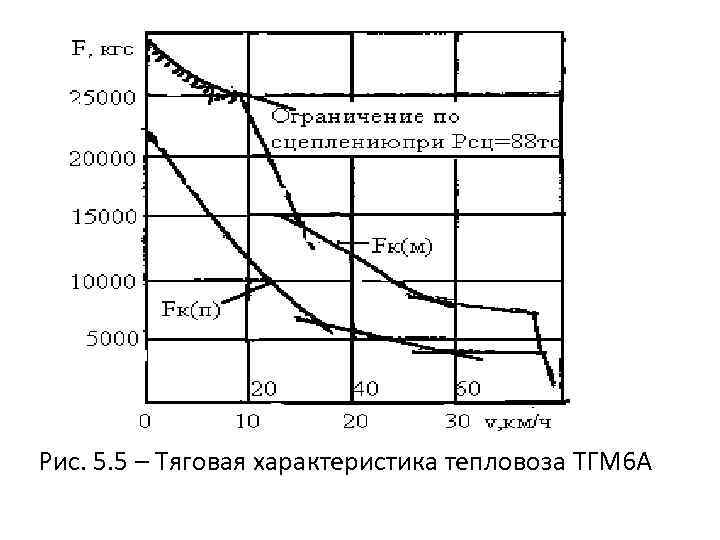 При установке главной рукоятки
на макси­мальную
позицию локомотив реализует предельную
тяговую характеристику.

Локомотив | Определение, история, дизайн, типы и факты

тепловоз

; Сименс, Вернер фон

Смотреть все СМИ

Ключевые люди:

Ричард Тревитик
Джордж Стефенсон
Питер Купер
Джон Стивенс
Эжен Шнайдер

Похожие темы:

Большой мальчик
Бейер-Гаррат
железнодорожная муфта
электровоз
нежный

См. весь связанный контент →

Последние новости

17 апреля 2023 г., 19:30 по восточноевропейскому времени (AP)

Железная дорога штата Мэн вновь открывается через 2 дня после схода с рельсов и пожара сошедший с рельсов в выходные, вновь открылся после ремонта пути

23 марта 2023 г., 23:10 по восточноевропейскому времени (AP)

Должностные лица: Устройство безопасности сошло с рельсов из-за человеческой ошибки. Поезд в Вашингтоне

Федеральное управление железных дорог сообщает, что предотвратить опрокидывание поездов в Пьюджет-Саунд на прошлой неделе сбил поезд с рельсов, разлив 3100 галлонов дизельного топлива в штате Вашингтон

локомотив , любое из различных самоходных транспортных средств, используемых для буксировки железнодорожных вагонов по путям.

Хотя движущая сила поезда может быть встроена в вагон, в котором также есть пассажирские, багажные или грузовые помещения, чаще всего она обеспечивается отдельной единицей, локомотивом, который включает в себя оборудование для производства (или, в случае электровоза, для преобразования) мощности и передачи ее на ведущие колеса. Сегодня есть два основных источника энергии для локомотива: нефть (в виде дизельного топлива) и электричество. Пар, самая ранняя форма движения, использовался почти повсеместно примерно до времени Второй мировой войны; с тех пор он был заменен более эффективной дизельной и электрической тягой.

Паровоз был самодостаточной единицей, у которой был собственный запас воды для производства пара и угля, масла или дров для обогрева котла. Тепловоз также имеет собственный запас топлива, но мощность дизельного двигателя не может быть напрямую связана с колесами; вместо этого необходимо использовать механическую, электрическую или гидравлическую трансмиссию. Электровоз не самодостаточен; он получает ток от воздушного провода или третьего рельса рядом с ходовыми рельсами. Электроснабжение третьего рельса используется только городскими скоростными железными дорогами, работающими на низковольтном постоянном токе.

В 1950-х и 60-х годах газовая турбина была принята на вооружение одной американской и некоторыми европейскими железными дорогами в качестве альтернативы дизельному двигателю. Хотя его преимущества были сведены на нет прогрессом в технологии дизельной тяги и ростом цен на нефть, он по-прежнему предлагается в качестве альтернативного средства для создания высокоскоростного железнодорожного сообщения в регионах, где отсутствует инфраструктура для подачи электроэнергии.

Основные характеристики, которые сделали Rocket 9 Джорджа и Роберта Стефенсонов0046 1829 г. успешный — его многотрубный котел и его система отвода пара и создания тяги в топке — продолжали использоваться в паровозе до конца его карьеры. Вскоре количество спаренных ведущих колес увеличилось. Ракета имела только одну пару ведущих колес, но вскоре стали обычным явлением четыре спаренных колеса, и в конечном итоге некоторые локомотивы были построены с 14 спаренными машинистами.

Ведущие колеса паровозов были разных размеров, обычно больше для более быстрых пассажирских двигателей. В среднем было около 1829Диаметр –2032 мм (72–80 дюймов) для пассажирских двигателей и 1372–1676 мм (54–66 дюймов) для грузовых или смешанных типов транспорта.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас

Запасы топлива (обычно угля, но иногда нефти) и воды можно было перевозить на самой раме локомотива (в этом случае он назывался танковым двигателем) или в отдельном транспортном средстве, тендере, сцепленном с локомотивом. Тендер типичного европейского магистрального локомотива имел вместимость 9000 кг (10 тонн) угля и 30 000 литров (8 000 галлонов) воды. В Северной Америке были распространены более высокие мощности.

Для удовлетворения особых потребностей тяжелых грузовых перевозок в некоторых странах, особенно в Соединенных Штатах, большее тяговое усилие было получено за счет использования двух отдельных двигателей под общим котлом. Передний двигатель был сочленен или шарнирно соединен с рамой заднего двигателя, так что очень большой локомотив мог преодолевать повороты. Сочлененный локомотив изначально был швейцарским изобретением, первый из которых был построен в 1888 году.0045 Big Boy , используемый в горных грузовых перевозках на западе США. Big Boy весил более 600 коротких тонн, включая тендер. Он мог развивать тяговое усилие 61 400 кг (135 400 фунтов) и развивать мощность более 6000 лошадиных сил при скорости 112 км (70 миль) в час.

Одной из самых известных сочлененных конструкций был Beyer-Garratt, который имел две рамы, каждая из которых имела собственные ведущие колеса и цилиндры, увенчанные водяными баками. Два шасси разделяла еще одна рама, несущая котел, кабину и запас топлива. Этот тип локомотива был ценен на легко уложенных путях; он также мог преодолевать крутые повороты. Широко использовался в Африке.

Различные доработки постепенно улучшали поршневой паровоз. Некоторые из них включали более высокое давление в котле (до 2000–2060 килопаскалей [290–300 фунтов на квадратный дюйм] для некоторых из последних локомотивов по сравнению с примерно 1300 килопаскалей [200 фунтов на квадратный дюйм] для более ранних конструкций), перегрев, питательная вода. предварительный нагрев, роликовые подшипники и использование тарельчатых (перпендикулярных) клапанов вместо скользящих поршневых клапанов.

Тем не менее, тепловой КПД даже самых совершенных паровозов редко превышал 6 процентов. Неполное сгорание и потери тепла из топки, котла, цилиндров и других мест рассеивают большую часть энергии сгоревшего топлива. По этой причине паровоз устарел, но только медленно, потому что у него были компенсирующие преимущества, в частности его простота и способность выдерживать злоупотребления.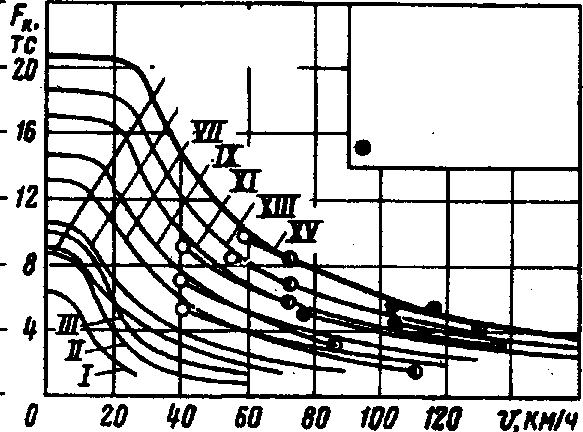

Попытки приведения в движение железнодорожных транспортных средств с помощью батарей датируются 1835 годом, но первое успешное применение электрической тяги было в 1879 году, когда на выставке в Берлине проехал электровоз. Первые коммерческие применения электрической тяги были на пригородных или городских железных дорогах. Один из первых произошел в 1895 году, когда Балтимор и Огайо электрифицировали участок пути в Балтиморе, чтобы избежать проблем с дымом и шумом в туннеле. Одной из первых стран, применивших электрическую тягу на магистральных линиях, была Италия, где система была запущена еще в 1902.

К началу Первой мировой войны в Европе и США действовало несколько электрифицированных линий. Крупные программы электрификации были предприняты после этой войны в таких странах, как Швеция, Швейцария, Норвегия, Германия и Австрия. К концу 1920-х годов почти в каждой европейской стране был хотя бы небольшой процент электрифицированных путей. Электрическая тяга также была введена в Австралии (1919 г. ), Новой Зеландии (1923 г.), Индии (1925 г.), Индонезии (1925 г.) и Южной Африке (1926 г.). Ряд столичных вокзалов и пригородных сообщений были электрифицированы в период с 19 по 19 век.00 и 1938 в Соединенных Штатах, и было несколько электрификаций основных линий. Появление тепловоза затормозило дальнейшую электрификацию магистральных маршрутов в Соединенных Штатах после 1938 года, но после Второй мировой войны такая электрификация была быстро распространена в других местах. Сегодня значительная часть колеи стандартной колеи на национальных железных дорогах по всему миру электрифицирована, например, в Японии (100 %), Швейцарии (92 %), Бельгии (91 %), Нидерландах (76 %), Испании ( 76 процентов), Италия (68 процентов), Швеция (65 процентов), Австрия (65 процентов), Норвегия (62 процента), Южная Корея (55 процентов), Франция (52 процента), Германия (48 процентов), Китай (42 процента). процентов) и Великобритании (32 процента). Напротив, в Соединенных Штатах, где имеется около 225 000 км (140 000 миль) путей стандартной колеи, электрифицированных маршрутов практически нет за пределами Северо-восточного коридора, где Amtrak управляет 720-километровым (450-мильным) экспрессом Acela Express между Бостоном и Вашингтоном. , округ Колумбия

Вторая половина века также была отмечена созданием в городах по всему миру множества новых электрифицированных городских систем скоростного железнодорожного транспорта, а также расширением существующих систем.

Преимущества и недостатки

Электрическая тяга обычно считается наиболее экономичным и эффективным средством эксплуатации железной дороги при условии, что доступна дешевая электроэнергия и плотность движения оправдывает большие капитальные затраты. Являясь просто энергопреобразующими, а не электрогенерирующими устройствами, электровозы имеют ряд преимуществ. Они могут использовать ресурсы центральной электростанции для выработки мощности, значительно превышающей их номинальные характеристики, для запуска тяжелого поезда или для преодоления крутого подъема на высокой скорости. Было замечено, что типичный современный электровоз мощностью 6000 лошадиных сил в течение короткого периода времени в этих условиях развивает до 10000 лошадиных сил. Кроме того, электровозы работают тише других типов и не выделяют дыма и дыма. Электровозам требуется мало времени в цехе для обслуживания, затраты на их обслуживание низки, а срок службы у них больше, чем у дизелей.

Самым большим недостатком электрифицированной эксплуатации являются высокие капитальные вложения и затраты на техническое обслуживание стационарного оборудования — проводов и сооружений тягового тока и электроподстанций, а также дорогостоящие изменения, которые обычно требуются в системах сигнализации для защиты их цепей от помех от электросети. высокие напряжения тягового тока и адаптировать их характеристики к превосходному ускорению и устойчивым скоростям, достигаемым за счет электрической тяги.

Динамический анализ тягового двигателя локомотива с учетом поверхностной волнистости на дорожках качения подшипника двигателя

В системе сцепки локомотив-гусеница транспортное средство приводится в движение тяговым двигателем, который подвешен на тележке и поддерживается колесной парой. Между тем усиленное взаимодействие колеса с рельсом создает огромные динамические нагрузки на тяговый двигатель через передачу вибрации. Следовательно, может оказаться необходимым рассмотреть вибрационную среду системы для исследования влияния волнистости дорожки на динамические характеристики тягового двигателя в процессе работы локомотива.

2.1 Модель пространственно-связанной динамики локомотив-пути с тяговыми передачами

На основе динамики сцепки локомотив-путь [15] предлагается модель пространственно-связанной динамики локомотив-путь с тяговыми передачами. Схема механической конструкции и подробный путь передачи мощности локомотива показаны на рис. 1а, б соответственно. Кузов вагона, тележка и колесная пара соединены вторичной и первичной подвесками. Тяговый двигатель и редуктор свинчиваются и поддерживаются колесной парой через подвесные подшипники. Подвесной шток мотор-редуктора выполнен в виде пружинно-демпфирующего элемента. Тяговый момент передается от тягового электродвигателя к стыку колесо-рельс через зубчатую передачу. Поскольку тяговый двигатель является источником энергии локомотива, его динамические характеристики могут напрямую влиять на устойчивость и безопасность системы транспортного средства. Кроме того, изменяющаяся во времени сила зацепления зубчатых колес является критическим внутренним возбуждением для системы локомотива. Соответствующая изменяющаяся во времени жесткость зубчатого зацепления может быть рассчитана с помощью усовершенствованного метода, предложенного Chen et al. [24].

Рис. 1

Структурная схема пространственно-сопряженной системы локомотив-путь: а система локомотив-путь, б тяговый двигатель, с зубчатая передача

Увеличенное изображение

Для тягового двигателя подсистемы, ротор и двигатель соединены через подшипники двигателя. Цилиндрический роликовый подшипник широко используется в тяговых двигателях для поддержки ротора, уменьшения эффекта трения и обеспечения точности вращения. Силы зубчатого зацепления действуют непосредственно на шестерню и существенно влияют на динамические характеристики тягового двигателя. Кроме того, вибрация системы, вызванная усиленными контактными силами, возникающими на границе раздела колесо-рельс, передается на тяговый двигатель через узлы локомотива и соответствующие соединительные элементы, что является важным внешним возбуждением для тягового двигателя. В этом разделе тяговый двигатель представлен в виде системы ротор-подшипник. В зависимости от поперечного расстояния между подшипником и шестерней, подшипники качения с более короткими/большими расстояниями определяются как подшипники ведущего/неприводного конца. Внутренние возбуждения (например, центробежная сила, неуравновешенное магнитное притяжение, сила трения, эксцентриситет силы тяжести и момент трения), вызванные динамическим эксцентриситетом ротора, всесторонне рассматриваются в этой модели. Вид с торца модели динамики локомотив-пути с тяговыми силовыми передачами показан на рис. 2.

Рис. 2

Завершающий обзор модели динамики локомотива и пути

Увеличенное изображение

2.

2 Динамическая модель подшипника качения

Учет динамических нагрузок, создаваемых или передаваемых от ротора ( W 3 4r 3 4r ) и двигателя ( W _m ), в этом разделе предлагается динамическая модель подшипника качения. Предполагается, что внутреннее и внешнее кольца закреплены на роторе и двигателе соответственно, а соответствующие контактные отношения игнорируются. Поэтому внутреннее и наружное кольца подшипников двигателя движутся и вращаются вместе с ротором и двигателем с одинаковой скоростью, а соответствующие внутренние силы взаимодействия подшипника качения действуют непосредственно на ротор и двигатель.

Как показано на рис. 3, внутренние силы подшипника качения включают контактные силы между роликом и обоймой, а также сепаратором и соответствующие силы трения. Кроме того, влиянием жесткости масляной пленки на входе и в зоне контакта на динамические характеристики подшипника качения можно пренебречь из-за огромной разницы в величине [25]. {2}}} R_{ {\text{m}}} } \hfill \\ \end{array} } \right.\;\;\;\;\;\left( {j = 1,2, \ldots ,N_{{\text {b}}} } \right),$$

(1)

где X _в и Z _в — относительные смещения между внутренней и внешней обоймами в продольном и вертикальном направлениях; σ _j — угловое положение j -го ролика; и — радиальный зазор подшипника; нижний индекс ‘ + ’ указывает на то, что значение в скобках будет равно нулю, если оно отрицательное; n – коэффициенты нагрузка–прогиб, где n  = 10/9 для цилиндрических роликоподшипников, а n  = 3/2 для шарикоподшипников; M _r — масса ролика; ω _{o j} – окружная скорость j -го ролика; R _м радиус делительной окружности подшипника; N _b — количество роликов; K _e — эквивалентная контактная жесткость между внутренней и внешней обоймами через ролик, которую можно рассчитать как 9{n} }},$$

(2)

где K _in и K _ou — изменяющаяся во времени контактная жесткость между роликом и внутренней/внешней обоймами соответственно.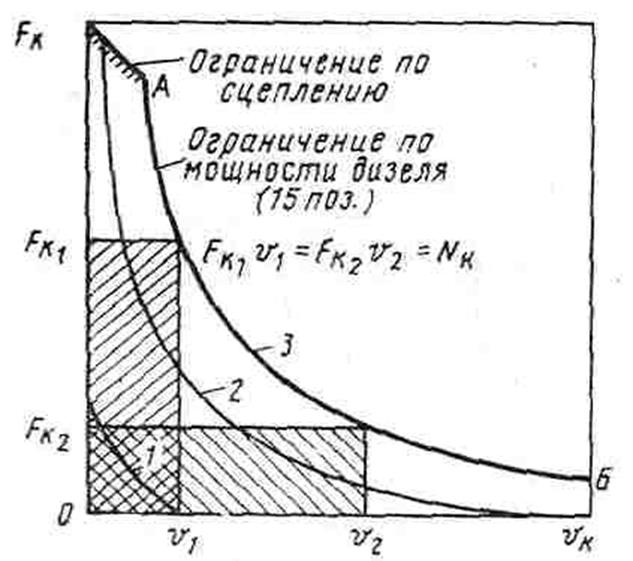

Угловое положение j -го ролика можно рассчитать как

$$\sigma _{j} = \sigma _{{\text{r}} j} + \left( {j — 1} \ справа)\frac{{2\uppi}}{{N_{\text{b}}}}\;\;\;\;\left( {j = 1,2, \ldots,N_{\text{b } } } \right),$$

(3)

где σ _{r j} – окружное угловое смещение j -го ролика.

Силы трения между j -м роликом и внутренним кольцом и между j -м роликом и наружным кольцом рассчитываются по формуле

$$\left\{ {\begin{array}{*{20} l} {F_{{{\text{in}}j}} = \mu _{{{\text{rr}}}} N_{{{\text{in}}j}} } \hfill \\ { F_{{{\text{ou}}j}} = \mu _{{{\text{rr}}}} N_{{{\text{ou}}j}} } \hfill \\ \end{массив } } \right.\;\;\;\left( {j = 1,2, \ldots ,N_{\text{b} } } \right),$$ 9{{ — c\Delta V}} + d,$$

(5)

где Δ V — скорость проскальзывания между роликом и дорожкой качения, а расчетные коэффициенты a , b , c и d могут быть выведены из тестовых значений.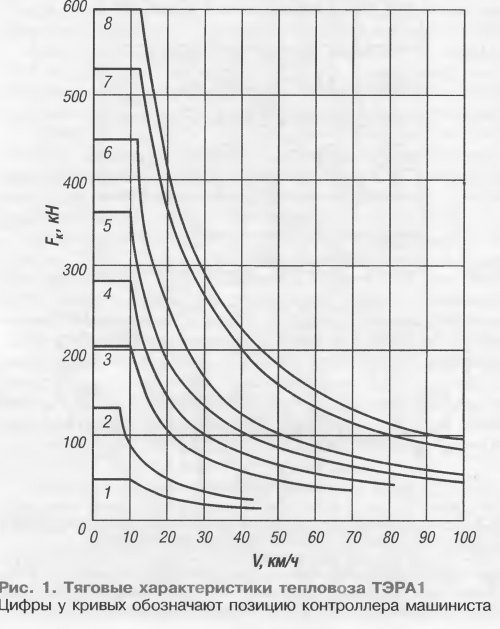

Сила контакта между роликом и сепаратором (\(N_{{{\text{c}}j}}\)) и соответствующие силы трения (\(F_{{{\text{c}}j}} \)) соответственно вычисляются следующим образом [29]:

$$N_{{{\text{c}}j}} = K_{{{\text{rc}}}} \left( {\sigma _{{{\text{r}}j}} — \sigma _{{\text{c}}} } \right) + C_{{{\text{rc}}}} \left( {\dot{ \sigma}_{{{\text{r}}j}} — \dot{\sigma}_{{\text{c}}} } \right)\;\;\;\;\;\left( {j = 1,2, \ldots ,N_{\text{b} } } \right),$$

(6)

$$F_{{{\text{c}}j}} = \mu _{{\text{c}}} N_{{{\text{c}}j}} \; \;\;\left( {j = 1,2, \ldots ,N_{\text{b} } } \right),$$

(7)

где K _rc и C _rc — контактная жесткость и демпфирование между роликом и сепаратором соответственно; μ _c — соответствующий коэффициент трения; σ _c — угловое смещение сепаратора при вращении.

Контактные усилия между роликом и ребрами внутреннего/наружного колец в поперечном направлении рассчитываются соответственно как

$$\left\{ {\begin{array}{*{20}l} {N_{{{\text{inr}}j}} = K_{{{\text{ry}}}} \left ( {Y_{{{\text{in}}}} — Y_{{{\text{r}}j}} } \right)} \hfill \\ {N_{{{\text{наш}}j} } = K_{{{\text{ry}}}} \left( {Y_{{{\text{r}}j}} — Y_{{{\text{ou}}}} } \right)} \ hfill \\ \end{array} } \right. \;\;\;\;\left( {j = 1,2, \ldots ,N_{\text{b} } } \right),$$

(8)

где K _ry — контактная жесткость между роликом и ребром; Д _в , Д 9{2} \ddot{\sigma}_{{{\text{r}}j}} — R_{{\text{m}}} \left( { — N_{{{\text{c}}j} } + F_{{{\text{in}}j}} — F_{{{\text{ou}}j}} — M_{{\text{r}}} g\sin \sigma _{j} } \right) = 0.$$

(10)

Самовращение j -го ролика:

$$I_{{{\text{ry}}}} \ddot{\theta }_ {{{\text{r}}j}} — R_{{\text{r}}} \left( {F_{{{\text{in}}j}} + F_{{{\text{ou} }j}} — F_{{{\text{c}}j}} } \right) = 0,$$

(11)

где θ _{r j 9{{N_{{\text{b}}} }} {N_{{{\text{c}}j}} } = 0,$$}

(13)

где I _c — момент инерции клети.

Следует отметить, что, принимая во внимание эффективность вычислений, эта подробная модель динамики подшипника используется только для рассматриваемого подшипника, в то время как для других, не рассматриваемых подшипников, они просто представлены в виде системы сосредоточенных пружинных масс без относительного проскальзывания между компоненты подшипника [30] или даже игнорируются в системе локомотив-пути.

2.3 Модель возбуждения волнистости поверхности подшипника

Как типичная геометрическая характеристика распределенного дефекта волнистость поверхности может существенно изменить геометрическую топографию дорожки качения и дополнительно повлиять на контактную жесткость в зоне контакта между роликом и дорожкой качения. Волнистость в виде чередующихся пиков и впадин; поэтому ее можно представить синусоидальной поверхностью [31]. Схема типа контакта между роликом и дорожкой качения с волнистостью поверхности или без нее показана на рис. 4. В этом исследовании модель возбуждения [10], связывающая изменяющееся во времени смещение и контактную жесткость, используется для анализа влияния равномерная волнистость поверхности подшипника двигателя.

Рис. 4

Схема контакта ролика с дорожками качения с волнистостью или без нее

Изображение в натуральную величину формулируется как [10]

$$\varDelta {{ = }}\varDelta _{{\text{0}}} {\text{ + }}\varDelta _{{\text{w}}} \sin \left( {\ frac {{2{\uppi}L_{{\text{w}}}}}{{\lambda _{{\text{w}}}}} + \sigma _{0}} \ справа),$$

(14)

где Δ _w — максимальная амплитуда волнистости; σ ₀ — начальный фазовый угол; λ _w — средняя длина волны; L _w – относительная длина дуги волны при краевом угле, которая может быть рассчитана как

$$\lambda _{{\text{w}}} = \frac{{2{\uppi }}}{{N_{{\text{w}}} }},$$

(15)

$$L_{{\text{w}}} = \left\{ {\begin{array} {*{20}l} {\sigma _{{{\text{ri}}}} R_{{{\text{in}}}} } \hfill & {{\text{(волнистость внутренней дорожки)}} } \hfill \\ {\sigma _{{{\text{ro}}}} R_{{{\text{ou}}}} } \hfill & {{\text{(волнистость внешней дорожки)}}} \ hfill \\ \end{массив} } \right. ,$$

(16)

где N _w — волновое число; R _в и R _или — радиусы внутренней и внешней обоймы соответственно; σ _ri и σ _ro — относительные углы контакта между роликом и внутренними/внешними кольцами соответственно, которые определяются как

$$\left\{ {\begin{array}{*{ 20}l} {\sigma _{{{\text{ri}}}} = \sigma _{j} — \theta _{{{\text{rot}}}}} \hfill & {{\text{ (волнистость внутренней дорожки)}}} \hfill \\ {\sigma _{{{\text{ro}}}} = \sigma _{j} — \theta _{{{\text{mot}}}}} \hfill & {{\text{(волнистость внешней дорожки)}}} \hfill \\ \end{array} } \right.,$$ 9{2} }}{{E_{2}}}\left( {\ln \frac{{2R_{{\text{ws}}}}}{{b_{{{\text{rc}}}}} } + 0,407} \справа)} \справа],$$

(20)

где Q — нормальная сила; L _c – контактная длина между роликом и волнистой дорожкой; ν ₁ и ν ₂ — коэффициент Пуассона материалов ролика и дорожки качения соответственно; E ₁ и E ₂ — соответствующие модули упругости; 9{2} }}{{E_{2} }}} \right)} . { 2} }} R_{{\text{m}}} } \hfill \\ \end{array} } \right.\;\;\;\;\left( {j = 1,2, \ldots ,N_ {{\text{b}}} } \right),$$ 9{n} }}\;\;\;\;\;\left( {j = 1,2, \ldots ,N_{\text{b} } } \right),$$

(24)

где K _{ew j} — изменяющаяся во времени эквивалентная контактная жесткость между внутренней и внешней обоймами через j -й ролик; K _{iw j} и K _{ow j} — изменяющаяся во времени контактная жесткость между роликом j th и волнистым внутренним и наружным кольцами соответственно; Δ _j — возбуждение смещения при угловом положении j -го ролика, которое можно рассчитать как

$$\varDelta _{j} = \varDelta _{{{\text{iw}}j }} + \varDelta _{{{\text{ow}}j}} \;\;\;\;\left( {j = 1,2, \ldots ,N_{\text{b} } } \right ),$$

(25)

где Δ _{iw j} и Δ _{ow j} — изменяющееся во времени возбуждение смещения, вызванное внутренней и внешней волнистостью качения на 0111 j -й ролик соответственно.