Содержание
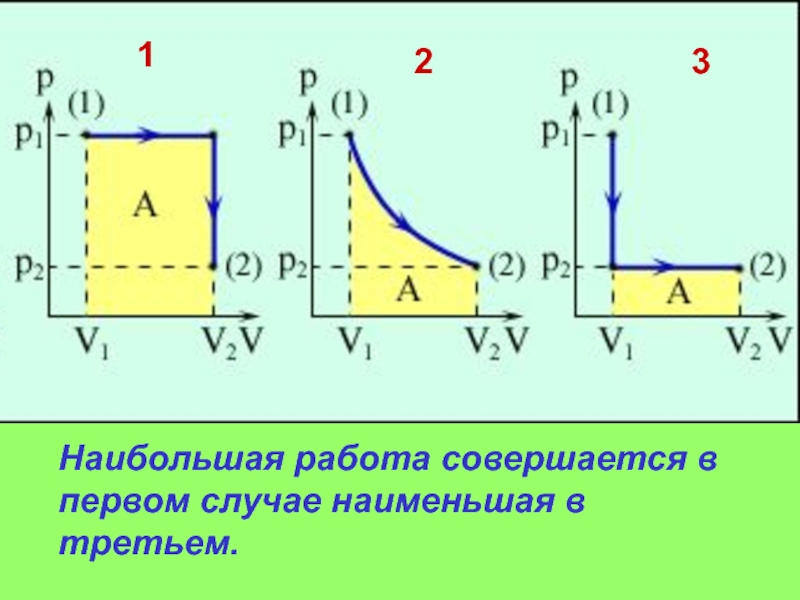
Два моля идеального газа совершают замкнутый цикл, изображенный на рисунке
Условие задачи:
Два моля идеального газа совершают замкнутый цикл, изображенный на рисунке. Известно, что температура \(T_1=280\) К, \(\frac{p_2}{p_1}=5\), \(\frac{T_4}{T_1}=2\). Чему равна работа, совершаемая газом за цикл?
Задача №5.5.51 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\nu=2\) моль, \(T_1=280\) К, \(\frac{p_2}{p_1}=5\), \(\frac{T_4}{T_1}=2\), \(A-?\)
Решение задачи:
Перестроим цикл, приведенный в условии в координатах p-T, в координатах p-V (смотрите схему к решению).
Работа газа за цикл \(A\) равна сумме работ газа в каждом из процессов, из которых состоит цикл. Работа газа в процессе численно равна площади фигуры под графиком процесса в координатах p-V, поэтому работа газа в процессах 1-2 и 3-4 равна нулю. Тогда:
\[A = {A_{23}} + {A_{41}}\;\;\;\;(1)\]
Работу газа \(A_{23}\) и \(A_{41}\) в изобарных процессах 2-3 и 4-1 найдём по таким известным формулам:
\[\left\{ \begin{gathered}
{A_{23}} = {p_2}\left( {{V_3} – {V_1}} \right) = {p_2}{V_3} – {p_2}{V_1} \hfill \\
{A_{41}} = {p_1}\left( {{V_1} – {V_3}} \right) = {p_1}{V_1} – {p_1}{V_3} \hfill \\
\end{gathered} \right. \]
\]
Запишем уравнение Клапейрона-Менделеева для состояния газа в точках 1-4:
\[\left\{ \begin{gathered}
{p_1}{V_1} = \nu R{T_1} \hfill \\
{p_2}{V_1} = \nu R{T_2} \hfill \\
{p_2}{V_3} = \nu R{T_3} \hfill \\
{p_1}{V_3} = \nu R{T_4} \hfill \\
\end{gathered} \right.\]
Тогда:
\[\left\{ \begin{gathered}
{A_{23}} = \nu R\left( {{T_3} – {T_2}} \right) \hfill \\
{A_{41}} = \nu R\left( {{T_1} – {T_4}} \right) \hfill \\
\end{gathered} \right.\]
Таким образом, формула (1) примет вид:
\[A = \nu R\left( {{T_3} – {T_2}} \right) + \nu R\left( {{T_1} – {T_4}} \right)\]
\[A = \nu R\left( {{T_3} – {T_2} + {T_1} – {T_4}} \right)\;\;\;\;(2)\]
Теперь все неизвестные температуры нужно выразить через известную температуру \(T_{1}\).
Процесс 1-2 – изохорный (\(V=const\)), запишем закон Шарля:
\[\frac{{{p_2}}}{{{T_2}}} = \frac{{{p_1}}}{{{T_1}}}\]
\[{T_2} = {T_1}\frac{{{p_2}}}{{{p_1}}}\]
Из условия задачи следует, что \(\frac{p_2}{p_1}=5\), поэтому:
\[{T_2} = 5{T_1}\;\;\;\;(3)\]
Аналогично, процесс 3-4 – изохорный (\(V=const\)), также запишем закон Шарля:
\[\frac{{{p_1}}}{{{T_4}}} = \frac{{{p_2}}}{{{T_3}}}\]
\[{T_3} = {T_4}\frac{{{p_2}}}{{{p_1}}}\]
Так как \(\frac{p_2}{p_1}=5\) и \(\frac{T_4}{T_1}=2\), то:
\[{T_3} = 5{T_4} = 10{T_1}\;\;\;\;(4)\]
Формула (2), учитывая выражения (3) и (4) и то, что по условию \({T_4} = 2{T_1}\), примет вид:
\[A = \nu R\left( {10{T_1} – 5{T_1} + {T_1} – 2{T_1}} \right)\]
\[A = 4\nu R{T_1}\]
Задача решена в общем виде, теперь посчитаем численный ответ:
\[A = 4 \cdot 2 \cdot 8,31 \cdot 280 = 18614,4\;Дж \approx 18,6\;кДж\]
Ответ: 18,6 кДж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
5.5.50 В каком из представленных на рисунке процессов AB, протекающих в данной массе газа
5.5.52 В некотором процессе газу сообщено 800 Дж теплоты, а его внутренняя энергия
5.5.53 В некотором процессе газу сообщено 900 Дж теплоты, а его внутренняя энергия
Простая физика — EASY-PHYSIC
Задачи средней сложности, для решения нужна только внимательность. Никаких «подвохов»- все математически четко и понятно.
Задача 1.
Температура идеального газа в состоянии 1 была . Чему равна температура в состоянии 3 после осуществления процесса 1-2-3, изображенного на диаграмме ? К.
К задаче 1
Процесс 1-2 – изохорный. Запишем закон Шарля.
Процесс 2-3 – не изотермический, поэтому просто запишем уравнение состояния:
Откуда
Ответ: 1800 К.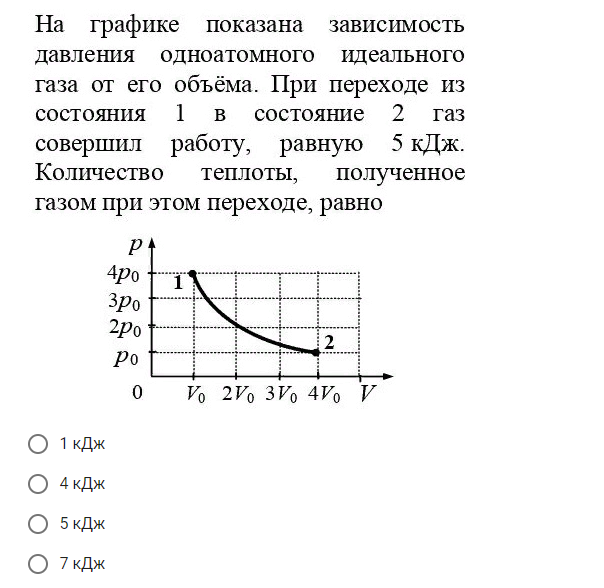
Задача 2.
Идеальный одноатомный газ, находящийся при нормальных условиях, переводят из состояния 1 в состояние 2 двумя способами: 1-3-2 и 1-4-2. Найдите отношение количеств теплоты, которые необходимо сообщить 1 кмоль газа в этих двух процессах.
К задаче 2
Рассмотрим переход 1-3-2. Процесс 1-3 – изохора, работа не совершается. Но температура растет, определим, как.
Процесс 3-2 – изобара. Работа в процессе 3-2 равна
Изменение температуры составило . Следовательно, можем определить изменение внутренней энергии:
Теперь найдем общее количество теплоты, переданное газу при таком переходе:
Процесс перехода 1-4-2 отличается только совершенной работой. Определим ее:
Определим отношение количеств теплоты:
Ответ: .
Задача 3.
Идеальный одноатомный газ, взятый в количестве 1 моль, переводят из состояния 1 в состояние 4.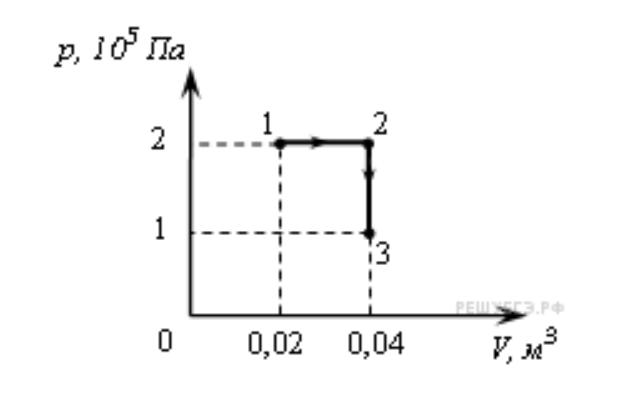 Какое количество теплоты сообщили в этом процессе газу? Масса газа во время процесса не меняется.
Какое количество теплоты сообщили в этом процессе газу? Масса газа во время процесса не меняется.
К задаче 3
Определим сначала изменение внутренней энергии, для этого составим объединенный газовый закон для точек 1 и 4.
Изменение внутренней энергии равно
Теперь определим работу. Работу удобно определить как площадь под кривой процесса. Разобьем эту площадь на удобные «куски» — трапеции.
К задаче 3. Определяем работу
Теперь найдем общее количество теплоты, переданное газу:
Ответ: 1450 Дж.
Задача 4.
На рисунке представлена диаграмма цикла с одноатомным идеальным газом, взятым в количестве 0,3 моль. Участки и — адиабаты. Определите работу, совершенную газом на участке .
К задаче 4
Участок по условию – адиабата, то есть передачи тепла газу на этом участке не происходит, следовательно, работа будет совершена за счет «внутренних резервов» — то есть внутренней энергии.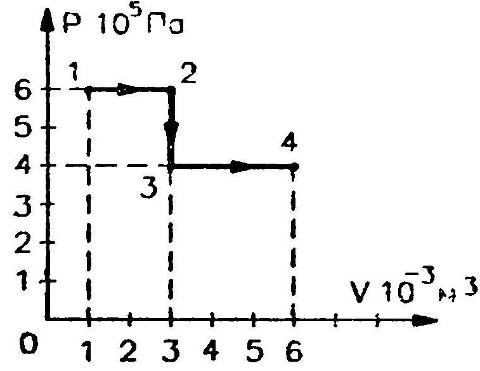 Нужно, следовательно, найти, как она изменилась.
Нужно, следовательно, найти, как она изменилась.
Задачу можно решить двумя способами. Во-первых, просто определить температуры в точках и , это легко сделать из данных графика с помощью уравнения Менделеева-Клапейрона, и затем посчитать . Но, так как , а ,то изменение внутренней энергии будет равно
Ответ: 1350 Дж.
Задача 5.
Один моль одноатомного идеального газа расширяется сначала изобарно, а затем по линейному закону, причем прямая линия проходит через начало координат . . Найдите , если количество тепла, сообщенное газу на участке 1-2, в 4 раза меньше работы, совершенной на участке 2-3.
К задаче 5
Определим количество тепла, сообщенное газу на участке 1-2, и работу, совершенную на участке 2-3.
Для изобарного процесса 1-2 запишем закон Гей-Люссака:
Откуда
Следовательно, изменение внутренней энергии газа равно
Работа на этом участке равна площади под графиком, под участком 1-2:
Тогда тепло, переданное газу, равно
Теперь рассмотрим процесс 2-3. Нам нужно определить лишь работу газа на этом участке. Площадь под этим участком – трапеция, поэтому
Нам нужно определить лишь работу газа на этом участке. Площадь под этим участком – трапеция, поэтому
Из подобия треугольников и запишем:
Тогда
Так как по условию , то
Так как , то
Сократим, что возможно:
Из первой записанной нами формулы (закона Гей-Люссака) следует, что
Тогда
Или
Введем замену :
Понятно, отрицательный корень нас не интересует.
Ответ: .
фазовых диаграмм | Химия для специальностей
Результаты обучения
- Объяснить построение и использование типичной фазовой диаграммы
- Использование фазовых диаграмм для идентификации стабильных фаз при заданных температурах и давлениях, а также для описания фазовых переходов, происходящих в результате изменения этих свойств
- Описать сверхкритическую флюидную фазу вещества
В предыдущем модуле было описано изменение равновесного давления паров жидкости в зависимости от температуры. Принимая во внимание определение точки кипения, графики зависимости давления пара от температуры показывают, как точка кипения жидкости зависит от давления. Описано также использование кривых нагрева и охлаждения для определения температуры плавления (или замерзания) вещества. Выполнение таких измерений в широком диапазоне давлений дает данные, которые можно представить графически в виде фазовой диаграммы. А 9Фазовая диаграмма 0013 объединяет графики зависимости давления от температуры для равновесий фазовых переходов жидкость-газ, твердое тело-жидкость и твердое тело-газ. На этих диаграммах показаны физические состояния, существующие при определенных условиях давления и температуры, а также приведена зависимость от давления температур фазовых переходов (температуры плавления, сублимации, кипения). Типичная фазовая диаграмма чистого вещества показана на рис. 1.
Принимая во внимание определение точки кипения, графики зависимости давления пара от температуры показывают, как точка кипения жидкости зависит от давления. Описано также использование кривых нагрева и охлаждения для определения температуры плавления (или замерзания) вещества. Выполнение таких измерений в широком диапазоне давлений дает данные, которые можно представить графически в виде фазовой диаграммы. А 9Фазовая диаграмма 0013 объединяет графики зависимости давления от температуры для равновесий фазовых переходов жидкость-газ, твердое тело-жидкость и твердое тело-газ. На этих диаграммах показаны физические состояния, существующие при определенных условиях давления и температуры, а также приведена зависимость от давления температур фазовых переходов (температуры плавления, сублимации, кипения). Типичная фазовая диаграмма чистого вещества показана на рис. 1.
Рис. 1. Физическое состояние вещества и температуры его фазовых переходов представлены графически на фазовой диаграмме.
Чтобы проиллюстрировать полезность этих графиков, рассмотрим фазовую диаграмму воды, показанную на рис. 2.
Рис. важные свойства.
Мы можем использовать фазовую диаграмму для определения физического состояния образца воды при определенных условиях давления и температуры. Например, давление 50 кПа и температура -10 °С соответствуют области диаграммы, обозначенной как «лед». В этих условиях вода существует только в твердом состоянии (лед). Давление 50 кПа и температура 50 °С соответствуют области «вода» — здесь вода существует только в виде жидкости. При 25 кПа и 200 °C вода существует только в газообразном состоянии. Обратите внимание, что на H 2 O фазовая диаграмма, оси давления и температуры не вычерчены в постоянной шкале, чтобы можно было проиллюстрировать несколько важных особенностей, как описано здесь.
Кривая BC на рисунке 2 представляет собой график зависимости давления паров от температуры, как описано в предыдущем модуле этой главы.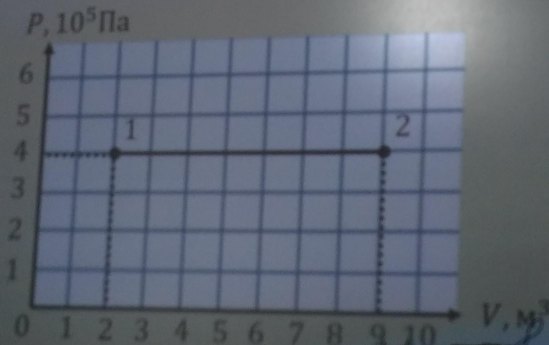 Эта кривая «жидкость-пар» разделяет жидкую и газообразную области фазовой диаграммы и дает точку кипения воды при любом давлении. Например, при 1 атм температура кипения составляет 100°С. Обратите внимание, что кривая жидкость-пар заканчивается при температуре 374 °C и давлении 218 атм, что указывает на то, что вода не может существовать в виде жидкости выше этой температуры, независимо от давления. Физические свойства воды в этих условиях занимают промежуточное положение между свойствами ее жидкой и газообразной фаз. Это уникальное состояние вещества называется сверхкритической жидкостью, и эта тема будет описана в следующем разделе этого модуля.
Эта кривая «жидкость-пар» разделяет жидкую и газообразную области фазовой диаграммы и дает точку кипения воды при любом давлении. Например, при 1 атм температура кипения составляет 100°С. Обратите внимание, что кривая жидкость-пар заканчивается при температуре 374 °C и давлении 218 атм, что указывает на то, что вода не может существовать в виде жидкости выше этой температуры, независимо от давления. Физические свойства воды в этих условиях занимают промежуточное положение между свойствами ее жидкой и газообразной фаз. Это уникальное состояние вещества называется сверхкритической жидкостью, и эта тема будет описана в следующем разделе этого модуля.
Рисунок 3 Сублимированные продукты, такие как это мороженое, обезвоживаются сублимацией при давлении ниже тройной точки для воды. (кредит: ʺlwaoʺ/Flickr)
Кривая твердого тела и пара, обозначенная AB на рис. 2, показывает температуры и давления, при которых лед и водяной пар находятся в равновесии. Эти пары данных температура-давление соответствуют точкам сублимации или осаждения воды. Если бы мы могли увеличить линию твердого газа на рисунке 2, мы бы увидели, что лед имеет давление паров около 0,20 кПа при температуре -10 °C. Так, если поместить замороженный образец в вакуум с давлением менее 0,20 кПа, лед возгонится. Это лежит в основе процесса «сублимационной сушки», часто используемого для сохранения пищевых продуктов, таких как мороженое, показанное на рис. 3.
Если бы мы могли увеличить линию твердого газа на рисунке 2, мы бы увидели, что лед имеет давление паров около 0,20 кПа при температуре -10 °C. Так, если поместить замороженный образец в вакуум с давлением менее 0,20 кПа, лед возгонится. Это лежит в основе процесса «сублимационной сушки», часто используемого для сохранения пищевых продуктов, таких как мороженое, показанное на рис. 3.
Кривая твердого тела и жидкости, обозначенная BD, показывает температуры и давления, при которых лед и жидкая вода находятся в равновесии, представляя точки плавления/замерзания воды. Обратите внимание, что эта кривая имеет небольшой отрицательный наклон (сильно преувеличенный для ясности), что указывает на то, что температура плавления воды немного снижается при увеличении давления. В этом отношении вода является необычным веществом, так как у большинства веществ температура плавления повышается с повышением давления. Такое поведение частично отвечает за движение ледников, подобное тому, что показано на рис. 4. Дно ледника испытывает огромное давление из-за своего веса, которое может растопить часть льда, образуя слой жидкой воды, на котором скользит ледник. может легче скользить.
4. Дно ледника испытывает огромное давление из-за своего веса, которое может растопить часть льда, образуя слой жидкой воды, на котором скользит ледник. может легче скользить.
Рис. 4. Огромное давление под ледниками приводит к их частичному таянию, образуя слой воды, обеспечивающий смазку, способствующую движению ледников. На этом спутниковом снимке показан наступающий край ледника Перито-Морено в Аргентине. (кредит: НАСА)
Точка пересечения всех трех кривых обозначена буквой B на рисунке 2. При давлении и температуре, представленных этой точкой, все три фазы воды сосуществуют в равновесии. Эта пара данных температура-давление называется тройная точка . При давлении ниже тройной точки вода не может существовать в жидком состоянии независимо от температуры.
Пример 1:
Определение состояния воды
Используя фазовую диаграмму для воды, приведенную на рисунке 10.30, определите состояние воды при следующих температурах и давлениях:
- -10 °C и 50 кПа
- 25 °C и 90 кПа
- 50 °C и 40 кПа
- 80 °C и 5 кПа
- −10 °C и 0,3 кПа
- 50 °C и 0,3 кПа
Показать раствор
Проверьте свои знания
Какие фазовые изменения может претерпевать вода при изменении температуры, если давление поддерживается на уровне 0,3 кПа? Если давление держится на уровне 50 кПа?
Показать решение
В качестве другого примера рассмотрим фазовую диаграмму диоксида углерода, показанную на рисунке 5. Кривая твердое тело-жидкость имеет положительный наклон, что указывает на то, что температура плавления CO 2 увеличивается с давлением, как и для большинства веществ (вода является заметным исключением, как описано ранее). Обратите внимание, что тройная точка намного выше 1 атм, что указывает на то, что углекислый газ не может существовать в виде жидкости в условиях атмосферного давления. Вместо этого охлаждение газообразного диоксида углерода до 1 атм приводит к его осаждению в твердом состоянии. Точно так же твердый диоксид углерода не плавится при давлении 1 атм, а возгоняется с образованием газообразного CO 9 .0025 2 . Наконец, обратите внимание, что критическая точка для углекислого газа наблюдается при относительно скромных температуре и давлении по сравнению с водой.
Кривая твердое тело-жидкость имеет положительный наклон, что указывает на то, что температура плавления CO 2 увеличивается с давлением, как и для большинства веществ (вода является заметным исключением, как описано ранее). Обратите внимание, что тройная точка намного выше 1 атм, что указывает на то, что углекислый газ не может существовать в виде жидкости в условиях атмосферного давления. Вместо этого охлаждение газообразного диоксида углерода до 1 атм приводит к его осаждению в твердом состоянии. Точно так же твердый диоксид углерода не плавится при давлении 1 атм, а возгоняется с образованием газообразного CO 9 .0025 2 . Наконец, обратите внимание, что критическая точка для углекислого газа наблюдается при относительно скромных температуре и давлении по сравнению с водой.
Рис. 5. Показана фазовая диаграмма диоксида углерода. Ось давления построена в логарифмическом масштабе, чтобы соответствовать большому диапазону значений.
Пример 2:
Определение состояния углекислого газа
Используя фазовую диаграмму для углекислого газа, показанную на рисунке 5, определите состояние CO 2 при следующих температурах и давлениях:
- −30 °C и 2000 кПа
- −60 °C и 1000 кПа
- −60 °C и 100 кПа
- 20 °C и 1500 кПа
- 0 °C и 100 кПа
- 20 °C и 100 кПа
Показать раствор
Проверьте свои знания
Определите фазовые превращения, которые претерпит диоксид углерода при повышении его температуры с -100 °C при постоянном давлении 1500 кПа.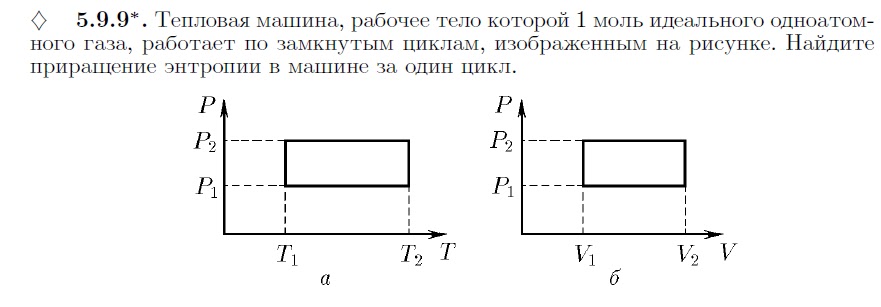 При 50 кПа. При каких примерных температурах происходят эти фазовые превращения?
При 50 кПа. При каких примерных температурах происходят эти фазовые превращения?
Показать решение
Сверхкритические жидкости
Если мы поместим образец воды в герметичный контейнер при температуре 25 °C, удалив воздух и позволив установиться равновесию испарения-конденсации, мы получим смесь жидкой воды и водяного пара при давление 0,03 атм. Отчетливо наблюдается четкая граница между более плотной жидкостью и менее плотным газом. По мере повышения температуры давление водяного пара увеличивается, как описано кривой жидкость-газ на фазовой диаграмме для воды (рис. 2), и сохраняется двухфазное равновесие жидкой и газообразной фаз. При температуре 374 °С давление пара возросло до 218 атм, и дальнейшее повышение температуры приводит к исчезновению границы между жидкой и паровой фазами. Вся вода в сосуде теперь находится в одной фазе, физические свойства которой занимают промежуточное положение между газообразным и жидким состояниями. Эта фаза вещества называется сверхкритическая жидкость , а температура и давление, выше которых существует эта фаза, являются критической точкой . При температуре выше критической газ не может сжижаться, какое бы давление ни применялось. Давление, необходимое для сжижения газа при его критической температуре, называется критическим давлением. Критические температуры и критические давления некоторых распространенных веществ приведены в таблице 1.
Эта фаза вещества называется сверхкритическая жидкость , а температура и давление, выше которых существует эта фаза, являются критической точкой . При температуре выше критической газ не может сжижаться, какое бы давление ни применялось. Давление, необходимое для сжижения газа при его критической температуре, называется критическим давлением. Критические температуры и критические давления некоторых распространенных веществ приведены в таблице 1.
| Таблица 1. | ||
|---|---|---|
| Вещество | Критическая температура (К) | Критическое давление (атм) |
| водород | 33,2 | 12,8 |
| азот | 126,0 | 33,5 |
| кислород | 154,3 | 49,7 |
| двуокись углерода | 304,2 | 73,0 |
| аммиак | 405,5 | 111,5 |
| диоксид серы 9{\circ}{\text{C}}[/латекс]) | Критическое давление (кПа) | |
| водород | -240,0 | 1300 |
| азот | -147,2 | 3400 |
| кислород | -118,9 | 5000 |
| двуокись углерода | 31,1 | 7400 |
| аммиак | 132,4 | 11 300 |
| диоксид серы | 157,2 | 7800 |
| вода | 374,0 | 22 000 |
Рис. 6. (а) Герметичный контейнер с жидким диоксидом углерода нагревается немного ниже его критической точки, что приводит к (б) образованию сверхкритической флюидной фазы. Охлаждение сверхкритической жидкости снижает ее температуру и давление ниже критической точки, что приводит к восстановлению отдельных жидких и газообразных фаз (c и d). Цветные поплавки иллюстрируют разницу в плотности между жидким, газообразным и сверхкритическим флюидным состоянием. (кредит: модификация работы «mrmrobin»/YouTube)
6. (а) Герметичный контейнер с жидким диоксидом углерода нагревается немного ниже его критической точки, что приводит к (б) образованию сверхкритической флюидной фазы. Охлаждение сверхкритической жидкости снижает ее температуру и давление ниже критической точки, что приводит к восстановлению отдельных жидких и газообразных фаз (c и d). Цветные поплавки иллюстрируют разницу в плотности между жидким, газообразным и сверхкритическим флюидным состоянием. (кредит: модификация работы «mrmrobin»/YouTube)
В этом видео наблюдайте за переходом диоксида углерода из жидкости в сверхкритическую жидкость.
Вы можете просмотреть стенограмму «Сверхкритический CO2» здесь (откроется в новом окне).
Подобно газу, сверхкритическая жидкость будет расширяться и заполнять контейнер, но ее плотность намного выше плотности обычных газов и обычно близка к плотности жидкостей. Подобно жидкостям, эти жидкости способны растворять нелетучие растворенные вещества. Однако они практически не проявляют поверхностного натяжения и имеют очень низкую вязкость, поэтому они могут более эффективно проникать в очень маленькие отверстия в твердой смеси и удалять растворимые компоненты. Эти свойства делают сверхкритические жидкости чрезвычайно полезными растворителями для широкого спектра применений. Например, сверхкритический диоксид углерода стал очень популярным растворителем в пищевой промышленности, его используют для декофеинизации кофе, удаления жиров из картофельных чипсов и извлечения вкусовых и ароматических соединений из цитрусовых масел. Он нетоксичен, относительно недорог и не считается загрязнителем. После использования CO 2 можно легко восстановить, снизив давление и собрав образовавшийся газ.
Подобно жидкостям, эти жидкости способны растворять нелетучие растворенные вещества. Однако они практически не проявляют поверхностного натяжения и имеют очень низкую вязкость, поэтому они могут более эффективно проникать в очень маленькие отверстия в твердой смеси и удалять растворимые компоненты. Эти свойства делают сверхкритические жидкости чрезвычайно полезными растворителями для широкого спектра применений. Например, сверхкритический диоксид углерода стал очень популярным растворителем в пищевой промышленности, его используют для декофеинизации кофе, удаления жиров из картофельных чипсов и извлечения вкусовых и ароматических соединений из цитрусовых масел. Он нетоксичен, относительно недорог и не считается загрязнителем. После использования CO 2 можно легко восстановить, снизив давление и собрав образовавшийся газ.
Пример 3:
Критическая температура углекислого газа
Если встряхнуть углекислотный огнетушитель в прохладный день (18 °C), можно услышать, как жидкий CO 2 плещется внутри цилиндра. Однако тот же самый цилиндр не содержит жидкости в жаркий летний день (35 °C). Объясните эти наблюдения.
Однако тот же самый цилиндр не содержит жидкости в жаркий летний день (35 °C). Объясните эти наблюдения.
Показать решение
Проверьте свои знания
Аммиак можно сжижать путем сжатия при комнатной температуре; кислород не может быть сжижен в этих условиях. Почему два газа ведут себя по-разному?
Показать решение
Декофеинизация кофе с использованием сверхкритического CO
2
Кофе является вторым наиболее широко продаваемым товаром в мире после нефти. Во всем мире люди любят аромат и вкус кофе. Многие из нас также зависят от одного компонента кофе — кофеина, который помогает нам двигаться утром или сохранять бодрость днем. Но в конце дня стимулирующий эффект кофе может помешать вам уснуть, поэтому вечером вы можете пить кофе без кофеина.
С начала 1900-х годов для удаления кофеина из кофе использовалось множество методов. У всех есть преимущества и недостатки, и все зависит от физических и химических свойств кофеина. Поскольку кофеин представляет собой несколько полярную молекулу, он хорошо растворяется в воде, полярной жидкости. Однако, поскольку многие из более чем 400 других соединений, влияющих на вкус и аромат кофе, также растворяются в H 2 O, процессы декофеинизации горячей водой также могут удалить некоторые из этих соединений, что отрицательно скажется на запахе и вкусе кофе без кофеина. Дихлорметан (СН 2 Cl 2 ) и этилацетат (CH 3 CO 2 C 2 H 5 ) имеют полярность, аналогичную кофеину, и поэтому являются очень эффективными растворителями для экстракции кофеина. но оба также удаляют некоторые компоненты вкуса и аромата, и их использование требует длительного времени экстракции и очистки. Поскольку оба этих растворителя являются токсичными, возникают опасения по поводу воздействия остаточного растворителя, остающегося в кофе без кофеина, на здоровье.
Поскольку кофеин представляет собой несколько полярную молекулу, он хорошо растворяется в воде, полярной жидкости. Однако, поскольку многие из более чем 400 других соединений, влияющих на вкус и аромат кофе, также растворяются в H 2 O, процессы декофеинизации горячей водой также могут удалить некоторые из этих соединений, что отрицательно скажется на запахе и вкусе кофе без кофеина. Дихлорметан (СН 2 Cl 2 ) и этилацетат (CH 3 CO 2 C 2 H 5 ) имеют полярность, аналогичную кофеину, и поэтому являются очень эффективными растворителями для экстракции кофеина. но оба также удаляют некоторые компоненты вкуса и аромата, и их использование требует длительного времени экстракции и очистки. Поскольку оба этих растворителя являются токсичными, возникают опасения по поводу воздействия остаточного растворителя, остающегося в кофе без кофеина, на здоровье.
Сверхкритическая флюидная экстракция с использованием диоксида углерода в настоящее время широко используется как более эффективный и экологически безопасный метод декофеинизации (рис. 7). При температуре выше 304,2 К и давлении выше 7376 кПа СО 2 — сверхкритическая жидкость, обладающая свойствами как газа, так и жидкости. Подобно газу, он проникает глубоко в кофейные зерна; подобно жидкости, он эффективно растворяет определенные вещества. Экстракция пропаренных кофейных зерен сверхкритическим диоксидом углерода удаляет 97-99% кофеина, оставляя вкусовые и ароматические соединения кофе нетронутыми. Поскольку CO 2 представляет собой газ при стандартных условиях, его удаление из экстрагированных кофейных зерен осуществляется легко, как и извлечение кофеина из экстракта. Кофеин, извлеченный из кофейных зерен с помощью этого процесса, является ценным продуктом, который впоследствии можно использовать в качестве добавки к другим продуктам питания или лекарствам.
7). При температуре выше 304,2 К и давлении выше 7376 кПа СО 2 — сверхкритическая жидкость, обладающая свойствами как газа, так и жидкости. Подобно газу, он проникает глубоко в кофейные зерна; подобно жидкости, он эффективно растворяет определенные вещества. Экстракция пропаренных кофейных зерен сверхкритическим диоксидом углерода удаляет 97-99% кофеина, оставляя вкусовые и ароматические соединения кофе нетронутыми. Поскольку CO 2 представляет собой газ при стандартных условиях, его удаление из экстрагированных кофейных зерен осуществляется легко, как и извлечение кофеина из экстракта. Кофеин, извлеченный из кофейных зерен с помощью этого процесса, является ценным продуктом, который впоследствии можно использовать в качестве добавки к другим продуктам питания или лекарствам.
Рис. 7. (a) Молекулы кофеина имеют как полярные, так и неполярные области, что делает его растворимым в растворителях различной полярности. (b) На схеме показан типичный процесс удаления кофеина с использованием сверхкритического диоксида углерода.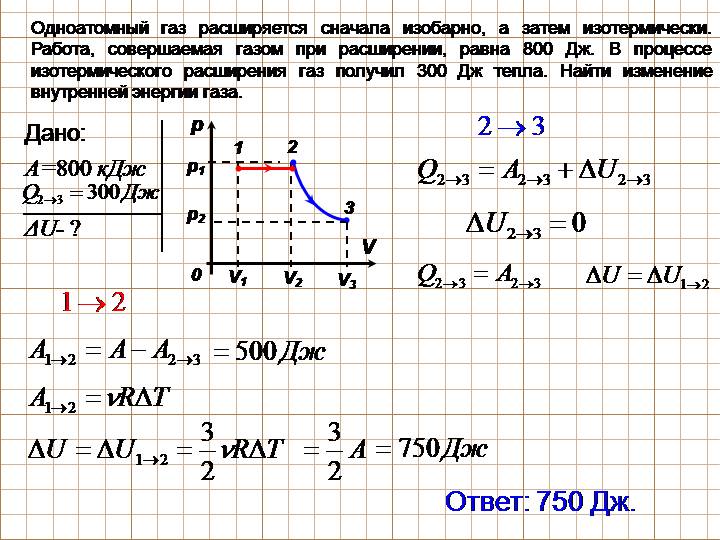
Ключевые понятия и резюме
Условия температуры и давления, при которых вещество существует в твердом, жидком и газообразном состояниях, представлены на фазовой диаграмме для этого вещества. Фазовые диаграммы представляют собой объединенные графики трех кривых равновесия давления и температуры: твердое тело-жидкость, жидкость-газ и твердое тело-газ. Эти кривые представляют отношения между температурами фазового перехода и давлениями. Точка пересечения всех трех кривых представляет тройную точку вещества — температуру и давление, при которых все три фазы находятся в равновесии. При давлениях ниже тройной точки вещество не может существовать в жидком состоянии независимо от его температуры. Конец кривой жидкость-газ представляет критическую точку вещества, давление и температуру, выше которых не может существовать жидкая фаза.
Попробуйте
- По фазовой диаграмме воды (рис. 2) определите состояние воды при:
- 35 °C и 85 кПа
- −15 °C и 40 кПа
- −15 °C и 0,1 кПа
- 75 °C и 3 кПа
- 40 °C и 0,1 кПа
- 60 °C и 50 кПа
- Какие фазовые превращения произойдут при воздействии на воду переменного давления при постоянной температуре 0,005 °С? При 40°С? При −40 °С?
- Скороварки позволяют готовить пищу быстрее, потому что более высокое давление внутри скороварки увеличивает температуру кипения воды.
 В некоторых скороварках есть предохранительный клапан, который выпускает пар, если давление превышает 3,4 атм. Какая приблизительная максимальная температура может быть достигнута внутри этой скороварки? Объясните свои рассуждения.
В некоторых скороварках есть предохранительный клапан, который выпускает пар, если давление превышает 3,4 атм. Какая приблизительная максимальная температура может быть достигнута внутри этой скороварки? Объясните свои рассуждения. - Из диаграммы состояния диоксида углерода на рисунке 5 определите состояние CO 2 при:
- 20 °C и 1000 кПа
- 10 °C и 2000 кПа
- 10 °C и 100 кПа
- −40 °C и 500 кПа
- −80 °C и 1500 кПа
- −80 °C и 10 кПа
- Определите фазовые превращения, которые претерпевает диоксид углерода при изменении давления, если поддерживать температуру на уровне -50 °C? Если поддерживать температуру минус 40 °С? При 20°С? (См. фазовую диаграмму на рисунке 5).
- Рассмотрим цилиндр, содержащий смесь жидкой двуокиси углерода, находящейся в равновесии с газообразной двуокисью углерода, при начальном давлении 65 атм и температуре 20 °С. Нарисуйте график, изображающий изменение давления в баллоне во времени при выделении газообразного диоксида углерода при постоянной температуре.

- Сухой лед, CO 2 ( s ), не тает при атмосферном давлении. Возгоняется при температуре -78°С. При каком минимальном давлении CO 2 ( s ) расплавится с образованием CO 2 ( l )? Примерно при какой температуре это произойдет? (См. фазовую диаграмму на рис. 5.)
- Если сильный шторм привел к отключению электричества, может потребоваться использование бельевой веревки для сушки белья. Во многих частях страны в разгар зимы одежда быстро замерзает, если ее повесить на веревку. Если не будет снега, они все равно высохнут? Поясните свой ответ.
- Можно ли сжижать азот при комнатной температуре (около 25 °C)? Можно ли сжижать диоксид серы при комнатной температуре? Объясните свои ответы.
- Элементарный углерод имеет одну газовую фазу, одну жидкую фазу и три различные твердые фазы, как показано на фазовой диаграмме:
- На фазовой диаграмме обозначьте газовую и жидкую области.
- Графит является наиболее стабильной фазой углерода при нормальных условиях.
 На фазовой диаграмме обозначьте графитовую фазу.
На фазовой диаграмме обозначьте графитовую фазу. - Если графит при нормальных условиях нагреть до 2500 К при повышении давления до 10 5 атм, то он превращается в алмаз. Обозначьте алмазную фазу.
- Обведите каждую тройную точку на фазовой диаграмме.
- В какой фазе существует углерод при 4000 К и 10 5 атм?
- Если температуру образца углерода увеличить с 4000 К до 5000 К при постоянном давлении 10 2 атм, какой фазовый переход произойдет, если произойдет?
Показать выбранные решения
Глоссарий
критическая точка: температура и давление, выше которых газ не может сконденсироваться в жидкость
фазовая диаграмма: график давление-температура, обобщающий условия, при которых могут существовать фазы вещества
сверхкритическая жидкость: вещество при температуре и давлении выше его критической точки; проявляет свойства, промежуточные между газообразным и жидким состояниями
тройная точка: температура и давление, при которых паровая, жидкая и твердая фазы вещества находятся в равновесии
Калькулятор закона Бойля
Создано Wojciech Sas, PhD
Отредактировано Bogna Szyk и Jack Bowater
Последнее обновление: 17 февраля 2023 г.
Содержание:
- Определение закона Бойля
- Формула закона Бойля 006
- Примеры закона Бойля
- Где находится Закон Бойля применяется?
- Другие термодинамические процессы
- Часто задаваемые вопросы
Калькулятор закона Бойля является отличным инструментом, когда вам нужно оценить параметры газа в изотермическом процессе . Вы найдете ответ на вопрос «Что такое закон Бойля?» в тексте, поэтому читайте дальше, чтобы узнать о формуле закона Бойля , увидеть несколько практических примеров упражнений по закону Бойля и узнать, как распознать, когда процесс удовлетворяет закону Бойля на графике.
Если вам нужно рассчитать результаты изобарического процесса, воспользуйтесь нашим калькулятором закона Чарльза.
Определение закона Бойля
Закон Бойля (также известный как закон Бойля-Мариотта) говорит нам о взаимосвязи между давлением газа и его объемом при постоянной температуре и массе газа . В нем говорится, что абсолютное давление обратно пропорционально объему .
В нем говорится, что абсолютное давление обратно пропорционально объему .
Определение закона Бойля можно также сформулировать следующим образом: произведение давления и объема газа в замкнутой системе постоянно, пока не изменяется температура.
Закон Бойля описывает поведение идеального газа. Мы можем охарактеризовать этот газ уравнением идеального газа, о котором вы можете прочитать больше в нашем калькуляторе законов идеального газа. Закон Бойля говорит нам о изотермический процесс , что означает, что температура газа во время перехода остается постоянной, как и внутренняя энергия газа.
Формула закона Бойля
Уравнение закона Бойля можно записать следующим образом:
p₁ × V₁ = p₂ × V₂ ,
где p₁ и 9 0013 V₁ — начальное давление и объем соответственно. Точно так же p₂ и V₂ являются конечными значениями этих параметров газа.
Мы можем записать формулу закона Бойля различными способами в зависимости от того, какой параметр мы хотим оценить. Допустим, мы изменили объем газа в изотермических условиях и хотим найти результирующее давление. Тогда уравнение закона Бойля утверждает, что:
p₂ = p₁ × V₁ / V₂ или p₂ / p₁ = V₁ / V₂ .
Как мы видим, соотношение конечного и начального давления является обратным отношением для объемов . Этот калькулятор закона Бойля работает в любом направлении, которое вам нравится. Просто введите любые три параметра, и четвертый будет рассчитан сразу!
Весь процесс можно представить на графике закона Бойля. Наиболее часто используется тип, когда давление является функцией объема. Для этого процесса кривая представляет собой гиперболу. Переход может происходить в обоих направлениях, поэтому и сжатие, и расширение газа удовлетворяют закону Бойля.
🔎 Если переход представляет собой изохорный процесс (постоянный объем), вам пригодится калькулятор закона Гей-Люссака Омни.
Примеры закона Бойля
Закон Бойля можно использовать несколькими способами, поэтому давайте рассмотрим несколько примеров:
Представьте, что у нас есть эластичный контейнер с газом. Начальное давление
100 кПа(или 10⁵ Па , если мы используем экспоненциальную запись), а объем сосуда равен2 м³. Решаем сжать ящик до1 м³, но общую температуру не меняем. Вопрос: «Как меняется давление газа?». Мы можем использовать формулу закона Бойля:p₂ = p₁ × V₁ / V₂ = 100 кПа × 2 м³ / 1 м³ = 200 кПа .
После уменьшения объема вдвое внутреннее давление удваивается. Это является следствием того, что произведение давления на объем должно быть постоянным в течение этого процесса.
Следующий пример закона Бойля относится к газу под давлением
2,5 атм, занимая6 литровпространства. Затем изотермически декомпрессируют до давления0,2 атм. Узнаем его окончательный объем. Мы должны переписать уравнение закона Бойля:
Узнаем его окончательный объем. Мы должны переписать уравнение закона Бойля:V₂ = p₁ × V₁ / p₂ = 2,5 атм × 6 л / 0,2 атм = 75 л .
Вы всегда можете воспользоваться нашим калькулятором закона Бойля, чтобы проверить правильность своих оценок!
Где применяется закон Бойля?
Закон Бойля описывает все процессы, при которых температура остается постоянной . В термодинамике температура измеряет среднюю кинетическую энергию, которой обладают атомы или молекулы. Другими словами, можно сказать, что средняя скорость частиц газа при этом переходе не меняется. Формула закона Бойля справедлива для широкого диапазона температур.
В расширенном режиме вы можете выбрать любую понравившуюся температуру, и мы рассчитаем количество молекул, содержащихся в газе. Вам нужно только следить за тем, чтобы вещество оставалось в газовой форме (например, не конденсировалось и не кристаллизовалось) при этой температуре.
Есть несколько областей, где применим закон Бойля:
Тепловая машина Карно – Состоит из четырех термодинамических процессов, два из которых изотермические, удовлетворяющие закону Бойля. Эта модель может сказать нам, каков максимальный КПД тепловой машины.
Дыхание тоже можно описать законом Бойля. Всякий раз, когда вы делаете вдох, ваша диафрагма и межреберные мышцы увеличивают объем легких, что снижает давление газа. Когда воздух течет из области более высокого давления в область более низкого давления, воздух попадает в легкие и позволяет нам получать кислород из окружающей среды. При выдохе объем легких уменьшается, поэтому давление внутри выше, чем снаружи, поэтому воздух течет в обратном направлении.
Шприц – Всякий раз, когда вам делают инъекцию, врач или медсестра сначала набирают жидкость из маленького флакона. Для этого они используют шприц. При вытягивании поршня доступный объем увеличивается, что снижает давление и, согласно формуле закона Бойля, вызывает всасывание жидкости.

Другие термодинамические процессы
Закон Бойля, наряду с законами Шарля и Гей-Люссака, относится к числу фундаментальных законов, описывающих подавляющее большинство термодинамических процессов.
Помимо определения значений конкретных параметров, таких как давление или объем, также можно узнать кое-что о теплопередаче и работе, выполненной газом во время этих переходов, а также изменении внутренней энергии . Мы собрали их все в нашем комбинированном газовом калькуляторе, где вы можете выбрать любой процесс и оценить результаты для реальных газов.
Часто задаваемые вопросы
Почему закон Бойля также называют изотермой?
Закон Бойля является одним из трех фундаментальных термодинамических процессов . В каждом из них изучается вариация двух из трех величин :
- давления ;
- температура ; и
- Том .

третья величина остается постоянной во время процесса. В случае закона Бойля мы не меняем температуру, поэтому мы называем процесс изотермическим .
Насколько расширится воздушный шар с начальным объемом 1000 см³ на крейсерской высоте?
Выполните следующие действия:
- Найдите начальное давление. Примем атмосферное давление на уровне моря: P i = 1 атм = 101 325 Па .
- Найдите конечное давление. В крейсерском самолете давление в кабине обычно составляет около P f = 0,8 атм = 81 060 Па .
- Рассчитайте окончательный объем по закону Бойля: V f = P i · V i /P f = (101,325 Па · 0,001 м 3 )/81 060 Па = 0,00125 м 3 9040 4 .
- Найдите расширение путем вычитания конечного и начального объемов: ΔV = V f — V i = (0,00125 — 0,001) м 3 = 0,00025 м 3 = 250 см 3 .

Как вычислить закон Бойля?
Для расчета закона Бойля нам нужно выполнить несколько простых действий, которые зависят от известных нам исходных данных. Если мы хотим вычислить конечное давление, и мы знаем начальный объем и давление, и конечный объем:
- Вычислить произведение начального объема и давления : В i · P i .
- Разделить результат на итоговый объем . Конечное давление равно P f = (V i · P i )/V f .
- Вы можете свободно инвертировать конечное и начальное значения (обратимое преобразование).
- Чтобы найти объем, просто переключите его нажатием на правую часть формулы.
Чему равно конечное давление, если объем уменьшится вдвое при начальном давлении 1 атм?
Конечное давление в процессе, когда объем уменьшается вдвое, начиная с P i = 1 атм , равно 2 .
 В некоторых скороварках есть предохранительный клапан, который выпускает пар, если давление превышает 3,4 атм. Какая приблизительная максимальная температура может быть достигнута внутри этой скороварки? Объясните свои рассуждения.
В некоторых скороварках есть предохранительный клапан, который выпускает пар, если давление превышает 3,4 атм. Какая приблизительная максимальная температура может быть достигнута внутри этой скороварки? Объясните свои рассуждения.
 На фазовой диаграмме обозначьте графитовую фазу.
На фазовой диаграмме обозначьте графитовую фазу. Узнаем его окончательный объем. Мы должны переписать уравнение закона Бойля:
Узнаем его окончательный объем. Мы должны переписать уравнение закона Бойля:

