Водоизмещающий режим, переходный, глиссирование

18.11.2019

 В этой статье мы рассмотрим режимы плаванья, виды судов и их скорость в разных режимах. В данной статье мы хотим наиболее простым языком описать механику движения судов, в частности, катамаранов и определение их максимальной скорости.

Стабильная скорость судна характеризуется равновесием воздействующих на него сил. Энергия мотора расходуется на создание поперечной волны, преодоление силы трения о поверхность воды и встречного ветра.

В состоянии покоя все суда в воде находятся в водоизмещающем режиме. Это означает, что они поддерживаются на поверхности воды только за счёт силы выталкивания. Скорость ограничена обводами судна. При движении на судно начинает воздействовать динамическая сила набегающего потока воды. С увеличением скорости сила потока увеличивается. Поток отражается от баллонов катамаранов или дна лодки. Если отразить поток в одном направлении вниз, то он позволяет вытолкнуть судно над водой (глиссирование). От круглых баллонов поток не отражается, а обтекает их, поэтому катамараны с круглыми баллонами не могут глиссировать. Для глиссирования нужно сделать нижнюю часть баллона плоской, чтобы поток отражался вниз. Во время глиссирования скорость, в основном, ограничена характеристиками мотора и ветром, а не обводами судна.

Водоизмещающий режим

Это наиболее экономичный режим движения судна. В нем ходят все большие морские и речные суда. Скорость зависит от обводов судна и длины ватерлинии. Судно поддерживается на плаву исключительно за счёт силы выталкивания. 

Движение катамарана в водоизмещающем режиме

При увеличении скорости с 10 до 17 км/ч корма будет сползать в яму

• Оптимальная скорость составляет 8-10 км/ч. В этом режиме расходуется наименьшее количество топлива на расстояние. Это скорость любого максимально загруженного катамарана Мастеркат с двигателем 5 л.с. Судно идет без дифферента, волнообразование небольшое.
• Для не глиссирующих катамаранов с двигателями 5-10 л. с. с небольшой загрузкой (20-30% от грузоподъемности) Скорость составляет 17-22 км/ч – она не является оптимальной с точки зрения расхода топлива (это уже переходный режим), но является компромиссом между скоростью и экономичностью. Судно имеет небольшой дифферент на корму.
• При увеличении мощности до 20-25 л.с. скорость не превысит 28 км/ч. При скорости более 20 км/ч дифферент на корму и волнообразование сильно увеличиваются. Энергия мотора расходуется на «заталкивание» судна на носовую поперечную волну. Для преодоления этого эффекта мы разработали специальные глиссирующие катамараны, на которых баллоны оснащены скегами и скорость достигает 40 км/ч.

Переходный режим

С ростом скорости судна длина и амплитуда носовой поперечной волны продолжает увеличиваться. Появляется дифферент на корму. Энергия мотора расходуется на заталкивание судна на передний гребень волны. 

Переходный режим – режим движения в котором создается большая поперечная волна, присутствует дифферент на корму называется переходным, а силы набегающего потока воды не хватает, чтобы вытолкнуть судно из воды. При этом не все суда могут выйти из переходного режима, зависит от обводов судна.

Становится понятно, что преодоление носовой поперечной волны требует больших затрат энергии мотора, поэтому переходный режим является наименее оптимальным с точки зрения расхода топлива. Расход растет, а скорость увеличивается незначительно.

Чем мощнее мотор, тем глубже будет опускаться корма и выше нос. Энергия будет расходоваться на не на ускорение, а на волнообразование.

Глиссирование

Чтобы выйти из переходного режима нужно, чтобы набегающий поток вытолкнул судно вверх. При этом осадка судна снижается, и оно перестаёт создавать поперечную волну и тратить энергию на её преодоление. В этом глиссирующем режиме судно поддерживается на плаву в основном за счёт силы потока, а скорость ограничена только силой трения и силой ветра, а также шагом винта и оборотами мотора. 

Обычные круглые баллоны неглиссирующего катамарана

Баллоны со скегами на моделях К53S и К47S

В круглых баллонах обычных катамаранов набегающий поток не выталкивает катамаран вверх, он просто обтекает баллоны. Для того, чтобы вытолкнуть судно необходимо отразить поток воды в одном направлении вниз, для этого нужна плоская опора. Чтобы сделать баллон плоским, мы наклеиваем дополнительные маленькие баллоны снизу основного. Эти баллоны называются скегами.

Поток обтекает круглые баллоны

Баллоны со скегами отражают поток

Скеги создают глиссирующую подушку, которая позволяет вытолкнуть катамаран из воды. Мы разработали две серийные модели со скегами.

• Глиссирующий катамаран и тримаран К47S – судно с палубой 325х200 см. Минимальный мотор 10 л.с., рекомендуем от 15 л.с. и выше.
• Глиссирующий катамаран и тримаран К53S– судно с палубой 400х200 см. Минимальный мотор 15 л.с., рекомендуем от 20 л.с.

Выход в режим глиссирование (скорость при которой не образуется поперечная волна и пропадает дифферент на корму) происходит на 25 км/ч. Соотношение мощности мотора к выталкиваемому весу составляет 1 л.с. на 25 кг веса. Это означает, что мотор мощностью 10 л. с. Способен вывести в режим глиссирования 250 кг веса. Если вычесть вес глиссирующего катамарана К47S и мотор и бак, то остаётся 100кг полезной нагрузки. На практике скорость с одним пассажиром на К47S с мотором 9.9 л.с. составила 28 км/ч.

Прототип глиссирующего катамарана К47S с укороченной палубойГлиссер К47S

При этом катамараны глиссирующие катамараны Мастеркат со скегами имеют почти такие же характеристики в водоизмещающем режиме, как и другие катамараны. В режиме глиссирования они имеют очень высокую остойчивость и стабильность. 

Сравнение скорости катамаранов

При выборе глиссирующего катамарана необходимо учитывать мощность мотора, т.к. слабый мотор не сможет вытолкнуть катамаран. Для катамарана К47S мы рекомендуем от 10-25 л.с. При 10 л.с. Катамаран сможет глиссировать с одним человеком и небольшим количеством снаряжения. Для катамарана К53s оптимальным будет мотор от 20 л.с. Глиссирующий катамаран значительно расширяет географию путешествий и рыбалки.

Подтверждение теории

На фото ниже как раз виден небольшой прогиб в центре катамарана из-за того, что он опирается на 2 гребня. На другом фото видно как притапливается корма  и задирается нос. Однако, корма находится еще не в самой нижней точке, поэтому волнообразование не сильное.

Оптимальный водоизмещающий режим, дифферент отсутствует.

Начало переходного режима, дифферент на корму. Скорость 12-13 км/ч, поэтому дифферент не сильный.

Комментарии к Водоизмещающий режим, переходный, глиссирование

4. Переходные режимы электроприводов

4.1 Общая характеристика переходных режимов электроприводов, их классификация и понятие об оптимальных переходных процессах

Переходным процессом
или переходным режимом электропривода
называется режим его работы при переходе
от одного установившегося состояния к
другому, когда изменяется скорость,
ток, момент, ускорение. Причинами
возникновения переходных режимов
является либо изменение нагрузки, либо
воздействие на электропривод при
управлении им, т.е. пуск, торможение,
реверс и т.п. Они могут возникнуть в
результате аварии или других случайных
причин, например, при изменении величины
напряжения или частоты сети, несимметрии
напряжения по фазам, изменении порядка
следования фаз, полном исчезновении
напряжения, обрыве проводов и т.п. У
некоторых механизмов, таких как
кривошипно-шатунные прессы, ножницы,
подъемно-качающиеся столы некоторых
прокатных станов, установившихся режимов
вообще нет, а их рабочие режимы представляют
собой периодические переходные процессы.

Переходные режимы
играют огромную роль в работе электропривода
и механизма, и часто их характер
предопределяет производительность
механизма и качество выпускаемой
продукции. Поэтому их изучение имеет
большое практическое значение. Анализ
этих режимов дает возможность правильно
рассчитать мощность электродвигателя
и выбрать его, уменьшить расход энергии
при пуске и торможении, позволяет выявить
предельно допустимое с точки зрения
нагрева число включений в час двигателя
электропривода, работающего большую
часть времени в переходных режимах.

Лишь ограниченное
число механизмов допускает возможность
проектирования их электропривода без
учета характера протекания переходных
процессов. К ним относятся некоторые
редко пускаемые и длительно работающие
механизмы с простейшими пусковыми
устройствами, например, вентиляторы,
насосы, а также механизмы, в которых
производственный процесс настолько
груб, что к их электроприводу вообще не
предъявляется каких-либо особых
требований, кроме обеспечения заданной
мощности (бетономешалки, камнедробилки
и т.п.).

Характер переходного
режима электропривода зависит от свойств
рабочей машины, типа электродвигателя
и его режима работы, передачи. Теоретическое
рассмотрение переходных процессов с
учетом всех влияющих факторов часто
затруднителен, ибо не всегда можно
аналитически выразить законы изменения
отдельных параметров, или же поведение
электропривода в переходных режимах
описывается системой уравнений высоких
порядков. К счастью, далеко не во всех
случаях требуется детальный учет всех
факторов. Второстепенные факторы могут
не приниматься во внимание.

На протекание
переходных процессов значительное
влияние оказывает механическая,
электромагнитная и тепловая инерция.
Механическая инерция, характеризуемая
электромеханической постоянной Т_м,
зависит как от инерционных масс и
характера нагрузки М_с,
так и от электромеханических свойств
двигателя. Электромагнитная инерция
характеризуется электромагнитной
постоянной Т_э,
зависящей от L
и R
электрической цепи. Тепловая инерция
характеризуется постоянной времени
нагрева Т_н,
зависит от теплоемкости машины и ее
теплоотдачи. Поскольку тепловые процессы
протекают значительно медленнее
электромагнитных и механических, их
при анализе переходных процессов
электропривода не принимают во внимание.

Если механическая
инерция практически всегда ощутима и
сказывается на переходных процессах,
то электромагнитная инерция может быть
и несущественной и практически не влиять
на характер протекания процесса. В связи
с этим, когда не требуется очень большой
точности, учитывается только механическая
инерция. Переходные процессы в этом
случае называются механическими.

Если учитывается
только электромагнитная инерция
(например, в цепях возбуждения), переходные
процессы называются электромагнитными,
а если учитывается механическая и
электромагнитная инерция –
электромеханическими.

Переход из одного
установившегося состояния в другое
может совершаться по различным
траекториям. При управлении электроприводом
стремятся выбирать такие, которые
обеспечивают максимальное быстродействие,
минимум потерь энергии и динамических
нагрузок, максимум полезной работы и
оптимальные значения других показателей.

Наиболее часто
требуется обеспечить изменение скорости
электропривода за минимальное время
при ограничении момента двигателя.
Такие переходные процессы называются
оптимальными по быстродействию при
ограничении момента. Этому условию при
М_с=const
соответствует равномерно ускоренный
характер изменения скорости при
М=М_доп=const
(см. кривые 1 и 2 на рис. 4.1.1).

Если М_с=f(ω),
то скорость при реверсе в процессе
торможения и пуска должна изменяться
с различными ускорениями в случае
реактивного М_с,
как показано на рисунке.

Для некоторых
механизмов, например, пассажирских
лифтов, переходные процессы должны
протекать при строго ограниченном
ускорении. Условием минимальной
длительности переходного процесса
является поддержание постоянства
ускорения при различных нагрузках.
Такие переходные процессы называются
оптимальными по быстродействию при
ограничении ускорения ε.

В этом случае
зависимость ω=f(t)
должна оставаться неизменной при разных
М_с,
а момент двигателя
при этих разных М_с
будет изменяться.

Однако, в ряде
случаев момент двигателя не реагирует
на изменение нагрузки. В этом случае
для ограничения ε при любых М_с
допустимый пусковой момент двигателя
необходимо выбрать из условия:

Так вот, если М_пуск
выбран в соответствии с данным выражением
и при различных нагрузках остается
неизменным, ускорение электропривода
при возрастании нагрузки будет уменьшаться
и при М_с=М_с
макс примет
значение

Очевидно ε_мин<ε_доп
и время пуска по мере возрастания
нагрузки увеличится.

Для многих механизмов
наряду с необходимостью ограничения М
и ε требуется обеспечить плавность
протекания переходных процессов путем
ограничения производной
или так называемого рывка.
Такие переходные процессы называются
оптимальными при ограничении момента
или ускорения и рывка.

Необходимость
таких ограничений вызывается различными
причинами. Так, для двигателей постоянного
тока по условиям коммутации необходимо
ограничивать
,
следовательно, и.
Для пассажирских лифтов ограничение
рывка создает более комфортные условия
для людей, находящихся в лифте. Следует,
только, иметь в виду, что ограничение
производнойпри пуске электропривода влечет за
собой снижение быстродействия. Например,
при уменьшениявозрастает время пуска электропривода.

4.2 Уравнения электромеханического
переходного процесса электропривода
с линейной механической характеристикой
при М_с=constи ω₀=const

В большинстве
применяемых в промышленности
электроприводов, получающих питание
от сети, электромеханические переходные
процессы протекают при неизменном
напряжении U
или частоте f₁,
т.е. при ω₀=const.
При этих условиях они возникают в случае
изменения управляющего воздействия ω₀
или f₁
скачком (пуск, торможение, реверс) или
изменении нагрузки. Для ограничения
бросков тока и момента при пуске,
торможении до допустимых значений в
цепь якоря или ротора двигателя вводится
добавочное сопротивление. При этом
электромагнитная постоянная
силовой цепи значительно снижается, а
электромеханическая постоянная,
наоборот, увеличивается (уменьшается
жесткость β). Поэтому при работе двигателя
на пусковых характеристиках влиянием
электромагнитной инерции на течение
переходных процессов можно пренебречь,
считая.
Необходимость учета Т_э
обычно возникает при выходе двигателя
на естественную характеристику, когда
добавочные сопротивления полностью
выведены и влияние электромагнитной
инерции может быть существенным.

Получим уравнения
переходного процесса для общего случая
при Т_э≠0
и ненулевых начальных условиях.
Электромеханические переходные процессы
при жестких механических связях, т.е.
,
описываются уравнениями:

;

Найдя М из второго
уравнения и подставив в первое, получим
уравнение, разрешенное относительно
скорости ω.

Аналогично можно
получить уравнение, разрешенное
относительно момента М.

.
Здесь

Корни характеристического
уравнения этих дифференциальных
уравнений одинаковы и при

равны:

Общее решение этих
уравнений при m<4
имеет вид:

Постоянные
интегрирования A,
B,
C,
D
находятся из начальных условий.

При t=0
ω=ω_нач;
M=M_нач:

Подставляем эти
величины в уравнения 1 и 2

ω_нач=ω_c+A;
M_нач=М_с+С.
Отсюда
;
С=М_нач-М_с

:

отсюда

Т.о. законы изменения
ω и М будут такими:

При
корни характеристического уравнения
р₁=-α₁,
р₂=-α₂
и общее решение уравнений 1 и 2 будет
таким:

Коэффициенты А₁,
В_1,
С₁,
D₁
находятся аналогично A,
B,
C,
D.

Законы изменения
ω и М будут иметь следующий вид:

При
,
что бывает в редких случаях, р₁=р₂=α
и общее решение дифференциальных
уравнений 1 и 2 имеет вид:

Коэффициенты А₂,
В_2,
С₂,
D₂
находятся из начальных условий.

Полученные общие
зависимости ω=f(t)
и M=f(t)
в частных случаях существенно упрощаются,
если до начала переходного процесса
режим работы электропривода был
установившимся.

Во всех случаях,
когда двигатель работает на реостатных
характеристиках, Тэ пренебрежительно
мала и ее можно считать равной 0. Если
электромеханическая связь в системе
электропривода является жесткой,
уравнения переходного процесса можно
получить из соотношений 3 и 4, положив в
них
;.
Они имеют вид:

4. 3 Переходный процесс электропривода
с линейной механической характеристикой
при одно – и многоступенчатом пуске в
случае М_с=const;
ω₀=const

При пуске в одну
ступень переходный процесс описывается
уравнениями:

;

если увеличение
скорости происходит не от ω=0, а от
какого-то начального установившегося
значения, как показано на рис. 4.3.1“а”.

Закон изменения
ускорения

,
где

ε_нач
– начальное ускорение.

Уменьшение ε по
мере увеличения скорости объясняется
непрерывным уменьшением динамического
момента М_дин.
Кривые ω(t)
и M(t)
изображены на рис. 4.3.1“б”.

Если разгон идет
из неподвижного состояния, т.е. когда
ω_нач=0,
то

(рис. 4.3.2“а”).

Время разгона на
любом участке процесса до какой либо
промежуточной скорости ω_кон

Задаваясь временем
t
от 0 до найденного по формуле, можно
построить кривые ω=f(t)
и M=f(t).
Они изображены на рис. 4.3.1“б”.

Т.к. ω_кон=ω_c,
то
.
Поэтому практически процесс считается
закончившимся, когда разность между
установившимся и текущим значениями
скорости снижается до 2%, т.е.

или

При ω_нач=0,
ω_кон=ω_с-0,02ω_с=0,98
ω_с.
Поэтому

Обычно при расчете
принимается t=(3÷4)T_м.

Что касается Т_м,
ее можно определить, проведя касательную
в любой точке кривой ω=f(t)
или М=f(t),
как показано на 4.3.1“б” и рис. 4.3.2“б”,
или используя следующие выражения:

;
;;

Для расчета
переходного процесса при многоступенчатом
пуске сначала строится пусковая диаграмма
по ранее изложенным правилам задавшись
пусковым и переключающим моментами.
Она изображена на рис. 4.3.3“а”.

Для любой ступени
разгона время, в течение которого момент
изменяется от М₁
до М₂
может быть определено по формуле

Постоянная времени
для любой ступени разгона

Законы изменения
ω и М при разгоне на любой ступени
определяются согласно ранее приведенным
выражениям.

Для примера
рассчитаем переходный процесс на первой
и второй ступенях.

Постоянная времени

Время разгона на
первой ступени

Закон изменения
скорости на этой ступени

Закон изменения
момента на этой ступени

Значения ω_н1
и ω_с1
находятся из графика рис. 4.3.3 или
теоретически:

;

Здесь R₁
– полное сопротивление якорной или
роторной цепи ДНВ или АД.

Задаваясь временем
t
от 0 до t₁,
можно рассчитать по приведенным формулам
и построить кривые ω=f(t)
и M=f(t).

Постоянная времени
для второй ступени

Время разгона на
второй ступени

Закон изменения
скорости и момента на этой ступени

;

Значения ω_н2
и ω_с2
находятся из пусковой диаграммы
аналогично как и на первой ступени и
т. д.

Время разгона при
выходе на естественной характеристике
до скорости ω_с
принимается равным t_н=(3÷4)T_м,
где в Т_м
вместо ω_нх
подставляется ω_н.

4.4 Переходные процессы электропривода
с линейной механической характеристикой
при М_с=const; ω₀=constв тормозных режимах

Рассмотрим сначала
реверс, который заключается в торможении
противовключением с дальнейшим изменением
направления вращения и разгоне в
противоположную сторону. Если реверс
осуществляется при активном моменте
сопротивления М_с=const,
переходный процесс описывается
уравнениями, приведенными ранее для
двигательного режима, с той разницей,
что в этих уравнениях нужно поставить
знак минус перед ω_с
и перед М_нач.

На рис. 4.4.1 изображена
механическая характеристика, иллюстрирующая
переход из двигательного режима в режим
противовключения (“а”) и соответствующие
этому кривые переходного процесса ω(t)
и M(t).

Двигатель при
переводе его в режим противовключения
тормозится по линии ВС. Затем, если его
не отключить от сети, будет разгоняться
в обратном направлении по линии CD,
достигает скорости идеального холостого
хода (-ω₀)
и т.к. момент сопротивления активный,
переходит в режим рекуперации с отдачей
энергии в сеть (линия DE).
Равновесие наступит в т. Е, где М=М_с
и скорость -ω_с.
Такой процесс может быть, если в случае
подъема тяжелого груза двигатель
тормозится противовключением и при ω=0
не отключается и не затормаживается
механическими тормозами.

При реактивном
моменте сопротивления процесс разбивается
на два этапа. На первом этапе, являющемся
тормозным, момент М_c
и момент двигателя действуют согласно,
обеспечивая эффективное торможение.
Закон изменения ω и М описываются теми
же уравнениями что и при активном М_c.
Время торможения до ω=0

На втором этапе
происходит разгон в противоположном
направлении (после торможения и
остановки), если требуется реверс. Знак
М_с
меняется на противоположный. Уравнения,
описывающие переходный процесс будут
иметь такой же вид, как для режима пуска,
только ω_нач=0,
М_нач=М_п,
ω_с=-ω’_с,
т.е.

;

где М_п
– пусковой момент.

Время реверса

Механические
характеристики, соответствующие данному
режиму и кривые переходного процесса
приведены на рис. 4.4.2“а” и “б”.

При переходе
скорости через 0 динамический момент
М_дин
скачком изменяется от значения
М_дин=-(М_п+М_с)
до М_дин=-(М_п-М_с),
что вызывает соответствующее изменение
ускорения и в кривых ω=f(t)
и M=f(t)
появляется излом.

При динамическом
торможении законы изменения ω и М
описываются теми же уравнениями, что и
для реверса, т.е.

;

,

где
ω_с
– установившаяся скорость, определяемая
точкой пересечения механической
характеристики динамического торможения
и вертикали М_c
=const.

В случае активного
М_с
точка “B”,
соответствующая установившейся скорости
-ω_с2,
относится к случаю, когда этот момент
в начале процесса является тормозным,
что имеет место, например, при подъеме
груза, а точка “С” с установившейся
скоростью ω_с1
– к случаю, когда этот момент является
движущим, например, при спуске груза
(рис. 4.4.3“а”).

В случае торможения
при подъеме груза под действием тормозного
момента двигателя и М_с
привод вначале будет тормозится и
остановится, т.к. момент двигателя станет
равным 0, но т.к. М_с
является активным и будет продолжает
действовать в том же направлении, под
его действием система будет вращаться
в обратную сторону. При этом М_с
из тормозного превратится в движущий,
а тормозной момент двигателя изменит
свой знак и будет продолжать действовать
как тормозной. Установившаяся скорость
–ω_С2
наступит при равенстве момента двигателя
и М_с
т.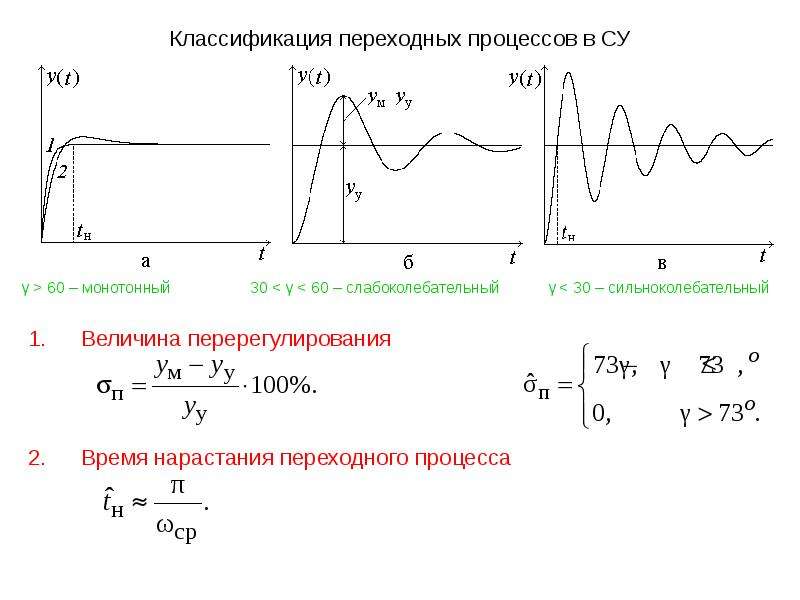 е. в точке “В”. Кривые переходного
процесса для этого случая изображены
на рис. 4.4.3“б”. Время торможения до
остановки.

Если активный
момент сопротивления М_с
в начале торможения был движущим
(торможение при спуске груза), то в начале
торможения тормозной момент двигателя
(отрезок ED
на рис. 4.4.3”а”) больше движущего
статического момента и имеет место
замедление, сопровождающееся уменьшением
тормозного момента двигателя. При
скорости ω_с1
M=M_c,
наступает установившийся режим тормозного
спуска груза со скоростью ω_с1.
В этом случае затормозить систему до
остановки путем динамического торможения
нельзя (рис. 4.4.3”в”).

При реактивном М_с
динамическое торможение происходит
так же, как и при подъеме груза. Разница
лишь в том, что при ω=0 действие М_с
прекратится, и т.к. момент двигателя
тоже станет равным 0, система остановится.
Соответствующие этому случаю механические
характеристики и кривые ω(t)
и М(t)
изображены на приведенных рис. 4.4.4
Процесс будет протекать так, как если
бы скорость ω стремилась стать равной
-ω_с,
но прекратится при ω=0. Поэтому
соответствующие отрезки кривых на
рисунке изображены пунктиром.

4.5 Переходные процессы электропривода
с линейной механической характеристикой
при ω₀=const, М_с=f(ω)

В случае линейной
М_c
от ω, т.е. при М_с=кω
дифференциальное уравнение, определяющее
поведении электропривода, имеет вид:

,
где

ω_y
– скорость установившегося режима при
М_с=М_y,
а ω_y
– падение скорости при установившемся
режиме (рис. 4.5.1).

Учитывая, что
ω_y+ω_y=ω₀
и умножая обе части уравнения на
,
получим

или

,

где

Решение этого
уравнения относительно ω и М дает законы
изменения ω и М

;

Длительность
переходного процесса

Здесь

– это время, за которое электропривод
разгонится до ω_y
при постоянном моменте, равном пусковому
М_п.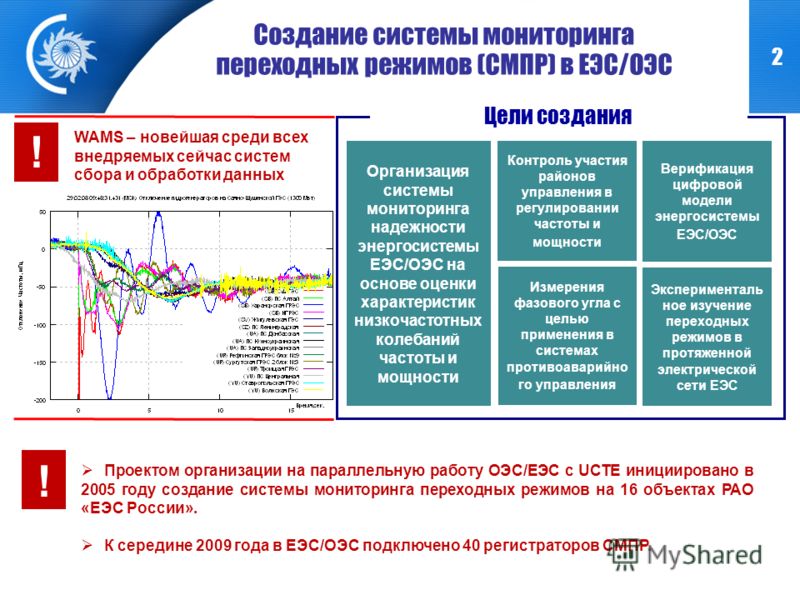

При М_с=М₀+К₁ω
и М_с=М₀-К₁ω
(рис. 4.5.2) переходный процесс описывается
этими же уравнениями, что и при М_с=Кω,
но в них

При вентиляторном
моменте сопротивления дифференциальное
уравнение, отражающее переходный
процесс, имеет вид:

Хотя это уравнение
решить можно, однако конечные результаты
малопригодны для практического
использования. Поэтому на практике чаще
используются графические и графоаналитические
методы. Естественно, что такие методы
дают лишь приближенные результаты,
однако, при тщательном выполнении их
точность достаточна для решения
практических задач. Правда, такие методы
имеют и такой недостаток: они не дают
возможности получить общие выводы.
Решение может быть найдено лишь для
частных случаев, когда значения всех
параметров электропривода известны.
Рассмотрим некоторые из них.

Переходные политические системы | Encyclopedia.

com

Переход — это интервал между двумя режимами. Многие политические системы вступают в переходный период, потому что их старый режим, то есть их правила, процедуры и институты, стали несостоятельными, и они остаются в переходном состоянии, потому что ни одному новому режиму не удается закрепиться. В начале двадцать первого века политологов особенно заинтересовали различные закономерности, формы и результаты переходов от тоталитарных и авторитарных режимов к демократическим режимам. Однако различные переходы не всегда приводят к демократическим режимам. Нередко происходит переход от одного типа авторитарного режима к другому типу авторитаризма. Когда переходный процесс движется к инаугурации демократического режима, общий процесс определяется как демократизация . Однако следует четко понимать, что не всякая демократизация приводит к демократической консолидации, то есть к режимам, которые можно считать и демократическими, и стабильными. Только демократические режимы, в которых общие политические и институциональные правила игры оспариваются лишь крошечным меньшинством, должны считаться консолидированными. Наконец, переход от авторитаризма к консолидированным демократическим режимам заканчивается исключительно тогда, когда демократия кажется большинству политических акторов «единственной игрой в городе». В таком случае предметом оспаривания станет не демократическая структура как таковая, а деятельность демократических властей.

волны демократизации

Демократия является не только концепцией, зародившейся в западной политической мысли, но и долгое время являлась западной практикой, ограниченной западными политическими системами. В широкой и убедительной сравнительно-исторической перспективе Сэмюэл П. Хантингтон (Huntington, 1991) утверждал, что мир политических систем прошел через три специфические волны демократизации и две обратные волны. Первая длинная волна демократизации (1828–1926 гг.) прокатилась по обе стороны Атлантики и охватила 33 страны. В основном это было продуктом трех факторов: (1) признание религиозного и политического инакомыслия; (2) постепенное расширение избирательного права и организация ассоциаций; (3) поощрение и защита гражданских и политических прав. Она усиливалась возможностью поглощения всех этих изменений в течение достаточно длительного периода времени и значительной степенью социально-экономического роста. Первая обратная волна (1922–1942) сократили количество демократий до одиннадцати. Он затронул демократические режимы, которым не удалось укрепиться и которые оставались непрочными и нелегитимными в глазах многих политических акторов. Во многом это было следствием потрясений, вызванных Первой мировой войной (1914–1918 гг.), Большевистской революцией в России (1917 г.) и фашистскими и нацистскими движениями в Европе (начиная с 1930-х годов). За эти двадцать неспокойных лет между двумя мировыми войнами все демократии столкнулись со многими трудностями и вынуждены были бороться в очень опасном мире, в котором авторитарные и тоталитарные режимы, казалось, расширялись и процветали, а уцелели немногие демократии, в основном самые старые.

Вторая волна демократизации (1943–1962 гг.) была по большей части следствием победы союзников во Второй мировой войне (1939–1945 гг. ). Были восстановлены некоторые демократические режимы, как, например, в Италии, Австрии, Германии и ряде стран Латинской Америки; другие были созданы недавно, как в Японии. Вторая волна увеличила количество демократических режимов до пятидесяти одного. Однако во второй послевоенный период под контроль советских войск попала не только вся территория Центральной и Восточной Европы.0003 коммунизм , но основная коммунистическая экспансия имела место в Азии, когда коммунистические режимы пришли к власти в Китае, Северной Корее и, позднее, во Вьетнаме. Вторая обратная волна произошла между 1958 и 1975 годами и затронула практически все латиноамериканские демократические режимы, за исключением Колумбии и Венесуэлы, сократив число уцелевших демократий до 29. Холодная война и реальный или искусственно созданный страх перед коммунизмом сыграли значительную роль в большинстве случаев военного вмешательства и военного правления. Третья волна демократизации началась в Южной Европе в 1974. Он был ответственен, во-первых, за возвращение Португалии, Греции и Испании к демократии, а затем, после падения Берлинской стены в ноябре 1989 г. , за установление демократических режимов в большинстве коммунистических стран Центральной и Восточной Европы. Третья волна вышла далеко за пределы западных границ; он затронул такие отдаленные страны, как Южная Корея, Южно-Африканская Республика и Тайвань, и достиг самого высокого зарегистрированного числа демократических режимов: шестьдесят два.

Согласно Хантингтону, третью волну демократизации обусловили пять факторов:

1. Углубление проблем легитимности авторитарных систем
2. Беспрецедентный глобальный социально-экономический рост 1960-х годов
3. Разительные изменения в доктрине и деятельности католической церкви Демократические реформаторы Южной Европы и выход Михаила Горбачева (р. 1931) из коммунистических режимов Центральной и Восточной Европы
4. Воздействие общественного инакомыслия и его последствия в обществе. В начале двадцать первого века было рискованно пытаться предсказать, готовится ли третья волна обратного движения. В целом общая обратная волна кажется маловероятной, хотя многие страны, в том числе, например, Нигерия, продолжают сползать в демократию и обратно. Однако возникает также вопрос, не достигло ли расширение демократии, по крайней мере на данный момент, своих внешних пределов.

Точнее, есть три географических региона, где демократия сталкивается с чрезвычайно серьезными трудностями при проникновении: Африка к югу от Сахары, Ближний Восток и некоторые районы Азии, особенно Китай. Большую часть Африки нельзя даже определить как страны с режимами, находящимися на грани перехода. На самом деле во всех африканских политических системах, за некоторыми исключениями, доминирует множество более или менее мягких авторитарных режимов. Такие политические системы не имеют социально-экономических условий, необходимых для создания предпосылок для перехода к демократии. То есть уровень образования не является ни хорошим, ни достаточно рассеянным, чтобы гарантировать существование политически осведомленных и активных граждан, а отсутствие экономического роста препятствует развитию социальных групп, желающих продвигать и поддерживать любой переход к демократии. Кроме того, в слишком многих случаях различные политические сообщества не имеют точного определения и по-прежнему сталкиваются с вызовом множества этнических группировок, которые не способствуют какой-либо политике компромисса. Хотя некоторые африканские авторитарные правители нестабильны и часто склонны к репрессиям и хищникам, они представляют собой временное решение проблемы политического порядка. Единственная осажденная демократия на Ближнем Востоке — это Израиль. Все остальные страны этого региона являются традиционными монархиями, султанаты , авторитарные режимы или даже, как в Иране, теократии. Большинство из них разделяют с остальным мусульманским миром очень важную, если не решающую роль, приписываемую мусульманскому духовенству, уламам , мусульманским религиозным школам, медресе и их толкованию Корана.

В некоторых случаях недемократические акторы, отдельная партия или военная организация являются единственным барьером против религиозного фундаментализма . Режимы, которые эти группы создают и поддерживают, почти неизбежно являются авторитарными. Без четкой границы между сферой религии и сферой политики демократизация мусульманского мира останется практически невозможной. Большинство переходов откроют больше политических возможностей для фундаменталистов, а не для модернизаторов, и тем более для демократических реформаторов. Азиатская версия коммунизма — единственное нерелигиозное политическое препятствие на пути демократизации ряда стран этого континента. Некоторые считают, что социально-экономический рост неизбежно приведет азиатские страны, в частности Китай, к переходу к демократическим режимам. После того, как азиатское население получило достойный уровень образования, приобрело значительный дохода на душу населения человек, переехавших в городские районы и подвергшихся воздействию средств массовой информации, необходимо будет приспособиться к давлению в пользу демократизации. Однако, несмотря на обеспеченность и высокообразованность населения, Сингапур остается примером стабильной авторитарной ситуации.

Есть также те, кто считает, что демократический процесс по сути является продуктом соглашения и компромисса между элитами, которые узнали цену конфронтации как для себя, так и для политической системы в целом. Это означает, что даже в стране, успешно прошедшей социально-экономическое развитие, если элиты останутся сплоченными и недемократическими, никакого перехода не произойдет. До сих пор это, кажется, имело место в коммунистическом Китае. На противоположной стороне спектра сплоченные, хотя и конкурентоспособные на выборах, элиты могут преуспеть в поддержании демократических рамок и демократических институтов вопреки всем социально-экономическим трудностям, как в современной Индии. Хантингтон резюмировал суть полемики о происхождении и выживании демократических режимов: «Экономическое развитие делает демократию возможной, политическое лидерство делает ее реальной» (Huntington 19).91, с. 316). Адам Пшеворски и его коллеги предложили другую точку зрения, согласно которой демократия может возникнуть на любом этапе, но «бедные» демократии умирают чаще.

схемы перехода и консолидации

Полное понимание переходных процессов должно основываться на знании режима, которому бросают вызов либерализаторы. Традиционным монархиям суждено потерять политическую власть, если и когда их попытки модернизации натолкнутся на сопротивление в королевском кругу и не будут считаться достаточно далеко идущими мобилизованными слоями общества, поддерживающими модернизация . В самом деле, традиционные монархии, похоже, не способны пережить политический и демократический переход, а тем более стать ведущими. Тоталитарные режимы, особенно основанные на абсолютном правлении и тотальной власти одной партии, обречены на крах, если они утратят способность контролировать свое общество и управлять своей экономической системой. Крах тоталитарного режима открывает путь к сложному переходу, характеризующемуся политическим беспорядком, потому что не существует другой организации, способной обрести легитимность и легитимным образом приобрести и осуществлять политическую власть. Авторитарные режимы, по-видимому, находятся в лучшем положении, когда вступают в переходный период, потому что по определению они сохранили и характеризовали, как выразился Хуан Линц, ограниченность плюрализм . Возрождение плюрализма, преобразованное в конкурентную и ответственную разновидность, позволяет осуществить переход к демократии, который, как в очень разных случаях Испании (1975–1982 гг.) и Польши (1988–1990 гг.), был более легким и более благоприятным для достижения жизнеспособных демократических результатов. .

Представляется, что решающим фактором во всех случаях успешного перехода является существование множества социальных, экономических и политических групп, конкурирующих в существенно однородной среде.0004 общество. Сильная и фрагментированная этническая, общинная и религиозная идентичность представляет собой наиболее важное препятствие не столько для самого перехода, сколько для самой консолидации режима-преемника. Действительно, как на Западе, так и на всех других континентах конфликты на почве этнической, общинной и религиозной принадлежности часто оказывались неразрешимыми. Следовательно, они обычно приводят к кровавым войнам и к созданию более мелких, более однородных, но также несколько конформистских и репрессивных сообществ. Всякий раз, когда эти конфликты не могут быть решены через интерэлиту, консоциативных соглашений или расколов и отделений политическая система не добьется никакой консолидации и останется в состоянии мучительного перехода.

Повторяющиеся переходы могут фактически характеризовать несколько политических систем, в которых условия для демократизации не материализуются. Режим может пережить переход от авторитаризма, но в то же время быть неспособным институционализировать демократический результат, только чтобы оказаться в новой авторитарной ситуации. Переход может произойти от мягкой авторитарной гражданской диктатуры к военному режиму или от султаната к однопартийному режиму или теократическому устройству. Большинство недемократических политических систем часто неспособны поддерживать свою старую и авторитарную конфигурацию и вынуждены, по крайней мере временно, перейти к демократической ситуации. Однако при отсутствии верховенство закона и достаточное количество убежденных сторонников демократии, новая, потенциально демократическая ситуация также становится несостоятельной. Переходы к демократии и от нее, характеризующиеся политическим беспорядком и случайными репрессиями, следуют друг за другом часто, если не периодически. Глобализация создала мировую среду, в которой информация о состоянии большинства политических систем широко доступна.

Существуют разные и конкурирующие интерпретации чередования авторитарных режимов и демократических экспериментов. Хотя, возможно, авторитарные режимы становятся более опытными в своих попытках свергнуть хрупкие демократические режимы и ужесточить свою власть, также верно и то, что демократии можно научиться путем экспериментов и адаптации. Демократы извлекут уроки из своих прошлых ошибок и придут к конструктивным компромиссам. Население в целом начнет ценить преимущества демократической среды. Сравнительный урок, по-видимому, заключается в том, что для того, чтобы стать и оставаться демократическими, все переходные политические системы должны найти необходимые ресурсы внутри себя.

промежуточная оценка

После почти двух столетий демократического развития в недемократических странах проживает не только больше недемократических, чем демократических режимов, но и гораздо больше людей живет в недемократических, чем в демократических странах, хотя эта ситуация во многом является результатом необычайной численности населения в недемократической республике Китая. Что трудно предсказать в начале двадцать первого века, так это не следующую обратную волну, а то, будет ли в краткосрочной перспективе еще одна волна перехода к демократии в некоторых других политических системах. С одной стороны, большинство существующих демократий кажутся достаточно консолидированными, чтобы не опасаться появления третьей волны реверса; с другой стороны, расширение демократии, похоже, достигло верхнего предела. Новые демократии могут появиться случайно, если и когда социально-экономические условия и способности политических лидеров будут усиливать друг друга. Следовательно, большинство ученых стало больше интересоваться качеством существующих демократий, чем переходом к дополнительным демократиям. Например, было проведено важное различие между «электоральными» демократиями и «либеральными» демократиями.

Выборы являются обязательным этапом перехода к демократическому режиму. Они должны быть бесплатными, справедливыми, конкурентными, периодическими и последовательными; то есть они должны привести к политическим последствиям, таким как возможность победить действующих должностных лиц . Однако существует четкое различие между политическими системами в

, в которых выборы проводятся, но избирательные кампании не являются свободными, а результатами выборов манипулируют, и режимами, в которых полностью соблюдается верховенство права. Последние режимы следует называть либеральными демократиями. Говоря более точно, либеральные демократии требуют, предоставляют и защищают:

1. Свобода вероисповедания, слова, организации, протеста и другие гражданские свободы
2. Равное отношение ко всем гражданам перед законом и надлежащей правовой процедурой
3. Политическая независимость и нейтралитет судебной власти
4. Открытое, плюралистическое гражданское общество
5. Гражданский контроль над вооруженными силами

Слишком во многих странах правители и государственные институты не могут или не желают защищать и продвигать права своих граждан, поддерживать верховенство закона и соблюдать его . В этих ситуациях свободные и конкурентные выборы по своей сути невозможны, и такие страны всегда будут подвержены риску перехода границы обратно к недемократическому правительству. Успешный переход к демократическим режимам должен поддерживаться путем поощрения и защиты прав личности. В гораздо большей степени, чем зачастую преждевременные выборы, эти права представляют собой прочную основу для начала переходного периода и построения прочного демократического режима.

См. также: Демократия.

библиография

Банс, Валери. «Сравнительная демократизация: большие и ограниченные обобщения». Сравнительные политические исследования 33 (2000): 703–734.

Даймонд, Ларри и Марк Ф. Платтнер. Глобальное расхождение демократий. Балтимор, Мэриленд: Издательство Университета Джона Хопкинса, 2001.

Ди Пальма, Джузеппе. Создание демократии: эссе о демократических преобразованиях. Беркли: University of California Press, 19.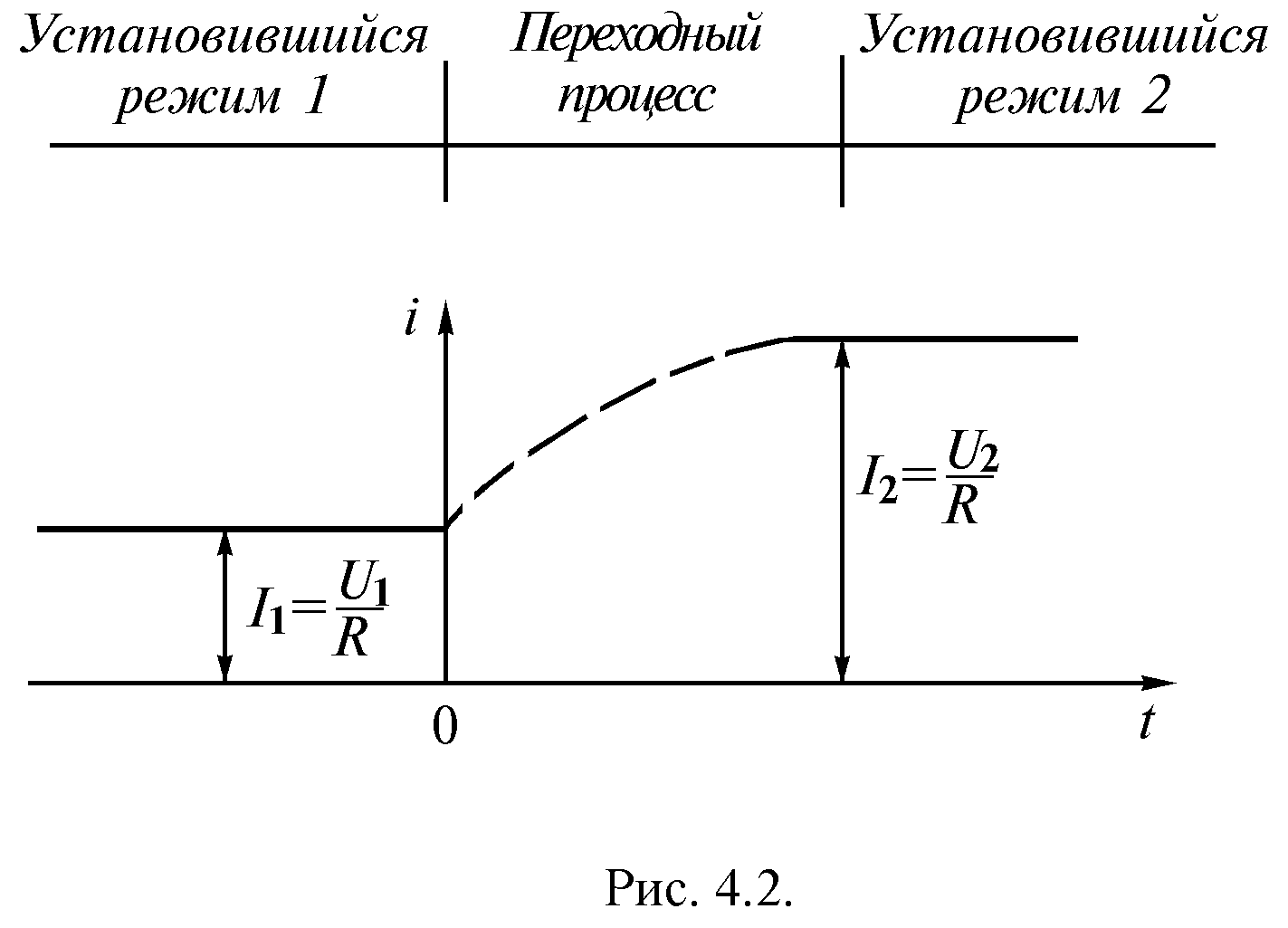 90.

Хантингтон, Сэмюэл П. Третья волна. Демократизация в конце ХХ века. Norman: University of Oklahoma Press, 1991.

Линц, Хуан Дж. и Альфред Степан. Проблемы демократического перехода и консолидации. Южная Европа, Южная Америка и посткоммунистическая Европа. Балтимор, Мэриленд: Издательство Университета Джона Хопкинса, 1996.

О’Доннелл, Гильермо, Филипп Шмиттер и Лоуренс А. Уайтхед, ред. Переходы от авторитарного правила , 4 тт. Балтимор, Мэриленд: Издательство Университета Джона Хопкинса, 1986.

Пшеворски, Адам, Майкл Э. Альварес, Хосе Антонио Шейбуб и Фернандо Лимонги. Демократия и развитие. Политические институты и благополучие в мире, 1050–1990 гг. Кембридж, Великобритания: Издательство Кембриджского университета, 2000.

Растоу, Данкварт А. «Переход к демократии: к динамической модели». Сравнительная политика 2 (1970): 337–363.

Ванханен, Туту. Процесс демократизации. Сравнительное исследование 147 штатов, 1980–1988. New York: Crane Russak, 1990.

Gianfranco Pasquino

Правительства стран мира: Глобальный справочник по правам и обязанностям граждан

Переходный режим | SpringerLink