Коэффициент полезного действия ?, формула КПД в физике. Как найти КПД⚡


Автор Даниил Леонидович На чтение 7 мин. Просмотров 47.8k. Опубликовано
Обновлено

Содержание

  1. Что такое КПД
  2. Примеры расчета КПД
  3. Единицы измерения
  4. От чего зависит величина КПД
  5. Как обозначается
  6. Символ, обозначающий КПД
  7. Мощность и КПД
  8. Формула работы в физике
  9. Это интересно

Что такое КПД

Коэффициент полезного действия машины или механизма – это важная величина, характеризующая энергоэффективность данного устройства. Понятие используется и в повседневной жизни. Например, когда человек говорит, что КПД его усилий низкий, это значит, что сил затрачено много, а результата почти нет. Величина измеряет отношение полезной работы ко всей совершенной работе.

Согласно формуле, чтобы найти величину, нужно полезную работу разделить на всю совершенную работу. Или полезную энергию разделить на всю израсходованную энергию. Этот коэффициент всегда меньше единицы. Работа и энергия измеряется в Джоулях. Поделив Джоули на Джоули, получаем безразмерную величину. КПД иногда называют энергоэффективностью устройства.

Если попытаться объяснить простым языком, то представим, что мы кипятим чайник на плите. При сгорании газа образуется определенное количество теплоты. Часть этой теплоты нагревает саму горелку, плиту и окружающее пространство. Остальная часть идет на нагревание чайника и воды в нем. Чтобы рассчитать энергоэффективность данной плитки, нужно будет разделить количество тепла, требуемое для нагрева воды до температуры кипения на количество тепла, выделившееся при горении газа.

Данная величина всегда ниже единицы. Например, для любой атомной электростанции она не превышает 35%. Причиной является то, что электростанция представляет собой паровую машину, где нагретый за счет ядерной реакции пар вращает турбину. Большая часть энергии идет на нагрев окружающего пространства. Тот факт, что η не может быть равен 100%, следует из второго начала термодинамики.

Примеры расчета КПД

Пример 1. Нужно рассчитать коэффициент для классического камина. Дано: удельная теплота сгорания березовых дров – 107Дж/кг, количество дров – 8 кг. После сгорания дров температура в комнате повысилась на 20 градусов. Удельная теплоемкость кубометра воздуха — 1,3 кДж/ кг*град. Общая кубатура комнаты – 75 кубометров.

Чтобы решить задачу, нужно найти частное или отношение двух величин. В числителе будет количество теплоты, которое получил воздух в комнате (1300Дж*75*20=1950 кДж ). В знаменателе – количество теплоты, выделенное дровами при горении (10000000Дж*8 =8*107 кДж).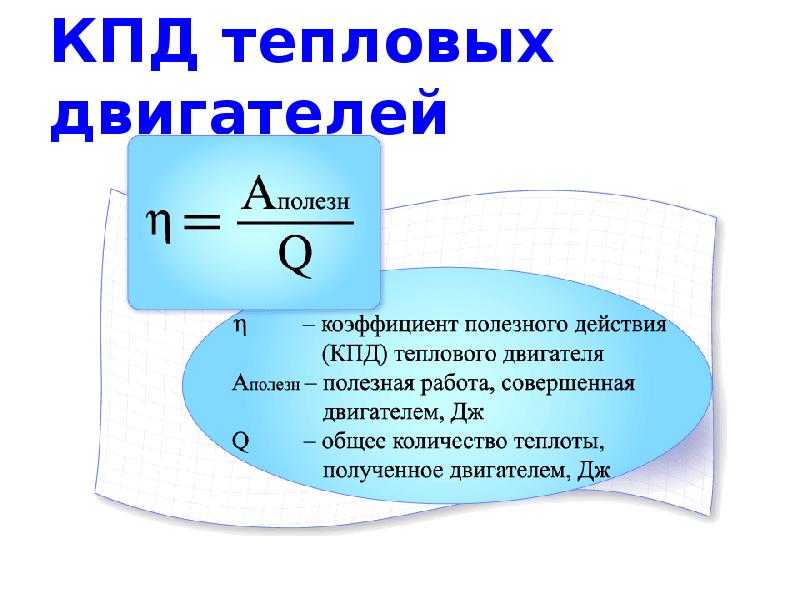 После подсчетов получаем, что энергоэффективность дровяного камина – около 2,5%. Действительно, современная теория об устройстве печей и каминов говорит, что классическая конструкция не является энергоэффективной. Это связано с тем, что труба напрямую выводит горячий воздух в атмосферу. Для повышения эффективности устраивают дымоход с каналами, где воздух сначала отдает тепло кладке каналов, и лишь потом выходит наружу. Но справедливости ради, нужно отметить, что в процессе горения камина нагревается не только воздух, но и предметы в комнате, а часть тепла выходит наружу через элементы, плохо теплоизолированные — окна, двери и т.д.

Пример 2. Автомобиль проделал путь 100 км. Вес машины с пассажирами и багажом – 1400 кг. При этом было затрачено14 литров бензина. Найти: КПД двигателя.

Для решения задачи необходимо отношение работы по перемещению груза к количеству тепла, выделившемуся при сгорании топлива. Количество тепла также измеряется в Джоулях, поэтому не придется приводить к другим единицам. A будет равна произведению силы на путь( A=F*S=m*g*S). Сила равна произведению массы на ускорение свободного падения. Полезная работа = 1400 кг x 9,8м/с2 x 100000м=1,37*108 Дж

Удельная теплота сгорания бензина – 46 МДж/кг=46000 кДж/кг. Восемь литров бензина будем считать примерно равными 8 кг. Тепла выделилось 46*106*14=6.44*108 Дж. В результате получаем η ≈21%.

Единицы измерения

Коэффициент полезного действия – величина безразмерная, то есть не нужно ставить какую-либо единицу измерения. Но эту величину можно выразить и в процентах. Для этого полученное в результате деления по формуле число необходимо умножить на 100%. В школьном курсе математики рассказывали, что процент – этот одна сотая чего-либо. Умножая на 100 процентов, мы показываем, сколько в числе сотых.

От чего зависит величина КПД

Эта величина зависит от того, насколько общая совершенная работа может переходить в полезную. Прежде всего, это зависит от самого устройства механизма или машины. Инженеры всего мира бьются над тем, чтобы повышать КПД машин. Например, для электромобилей коэффициент очень высок – больше 90%.

А вот двигатель внутреннего сгорания, в силу своего устройства, не может иметь η, близкий к 100 процентам. Ведь энергия топлива не действует непосредственно на вращающиеся колеса. Энергия рассеивается на каждом передаточном звене. Слишком много передаточных звеньев, и часть выхлопных газов все равно выходит в выхлопную трубу.

Как обозначается

В русских учебниках обозначается двояко. Либо так и пишется – КПД, либо обозначается греческой буквой η. Эти обозначения равнозначны.

Символ, обозначающий КПД

Символом является греческая буква эта η. Но чаще все же используют выражение КПД.

Мощность и КПД

Мощность механизма или устройства равна работе, совершаемой в единицу времени. Работа(A) измеряется в Джоулях, а время в системе Си – в секундах. Но не стоит путать понятие мощности и номинальной мощности. Если на чайнике написана мощность 1 700 Ватт, это не значит, что он передаст 1 700 Джоулей за одну секунду воде, налитой в него. Это мощность номинальная. Чтобы узнать η электрочайника, нужно узнать количество теплоты(Q), которое должно получить определенное количество воды при нагреве на энное количество градусов. Эту цифру делят на работу электрического тока, выполненную за время нагревания воды.

Величина A будет равна номинальной мощности, умноженной на время в секундах. Q будет равно объему воды, умноженному на разницу температур на удельную теплоемкость. Потом делим Q на A тока и получаем КПД электрочайника, примерно равное 80 процентам. Прогресс не стоит на месте, и КПД различных устройств повышается, в том числе бытовой техники.

Напрашивается вопрос, почему через мощность нельзя узнать КПД устройства. На упаковке с оборудованием всегда указана номинальная мощность. Она показывает, сколько энергии потребляет устройство из сети. Но в каждом конкретном случае невозможно будет предсказать, сколько конкретно потребуется энергии для нагрева даже одного литра воды.

Например, в холодной комнате часть энергии потратится на обогрев пространства. Это связано с тем, что в результате теплообмена чайник будет охлаждаться. Если, наоборот, в комнате будет жарко, чайник закипит быстрее. То есть КПД в каждом из этих случаев будет разным.

Формула работы в физике

Для механической работы формула несложна: A = F x S. Если расшифровать, она равна приложенной силе на путь, на протяжении которого эта сила действовала. Например, мы поднимаем груз массой 15 кг на высоту 2 метра. Механическая работа по преодолению силы тяжести будет равна F x S = m x g x S. То есть, 15 x 9,8 x 2 = 294 Дж. Если речь идет о количестве теплоты, то A в этом случае равняется изменению количества теплоты. Например, на плите нагрели воду. Ее внутренняя энергия изменилась, она увеличилась на величину, равную произведению массы воды на удельную теплоемкость на количество градусов, на которое она нагрелась.

Это интересно

Наукой обосновано, что коэффициент полезного действия любого механизма всегда меньше единицы. Это связано со вторым началом термодинамики.

Для сравнения, коэффициенты полезного действия различных устройств:

  • гидроэлектростанций 93-95%;
  • АЭС – не более 35%;
  • тепловых электростанций – 25-40%;
  • бензинового двигателя – около 20%;
  • дизельного двигателя – около 40%;
  • электрочайника – более 95%;
  • электромобиля – 88-95%.

Наука и инженерная мысль не стоит на месте. постоянно изобретаются способы, как уменьшить теплопотери, снизить трение между частями агрегата, повысить энергоэффективность техники.

Зависимость КПД теплового двигателя от свойств используемого газа

Чем плохо «изучение» цикла Карно и теоремы Карно? Тем, что вдалбливание этих «знаний» в еще неокрепшие и неопытные головы школьников и студентов формирует у них неверные стереотипные представления об окружающем нас мире.  При обучении педагогами не делается акцент на то, что цикл Карно – это всего-навсего так никогда и не реализованная идея по устройству «самого эффективного двигателя», который якобы сможет работать по замкнутому циклу.

Не пугайтесь, это не бесполезный и не реализуемый школьный цикл Карно. 🙂 Это пример, как на практике можно использовать теплоту для полезной работы — например, просто поднять груз не некоторую высоту.

Петр Иванович Дубровский, добросовестный инженер – исследователь, честный и непредвзятый частный научный детектив.

При обучении педагогами не делается акцент на то, что цикл Карно – это всего-навсего так никогда и не реализованная идея по устройству «самого эффективного двигателя», который якобы сможет работать по замкнутому циклу. При этом ни один из многочисленных авторов многочисленных школьных учебников ни одним словом не обмолвился о том, что:

1. Цикл Карно невозможно реализовать на практике.

2. Что никакая полезная работа в цикле Карно не выполняется, а, значит, КПД цикла Карно равно нулю.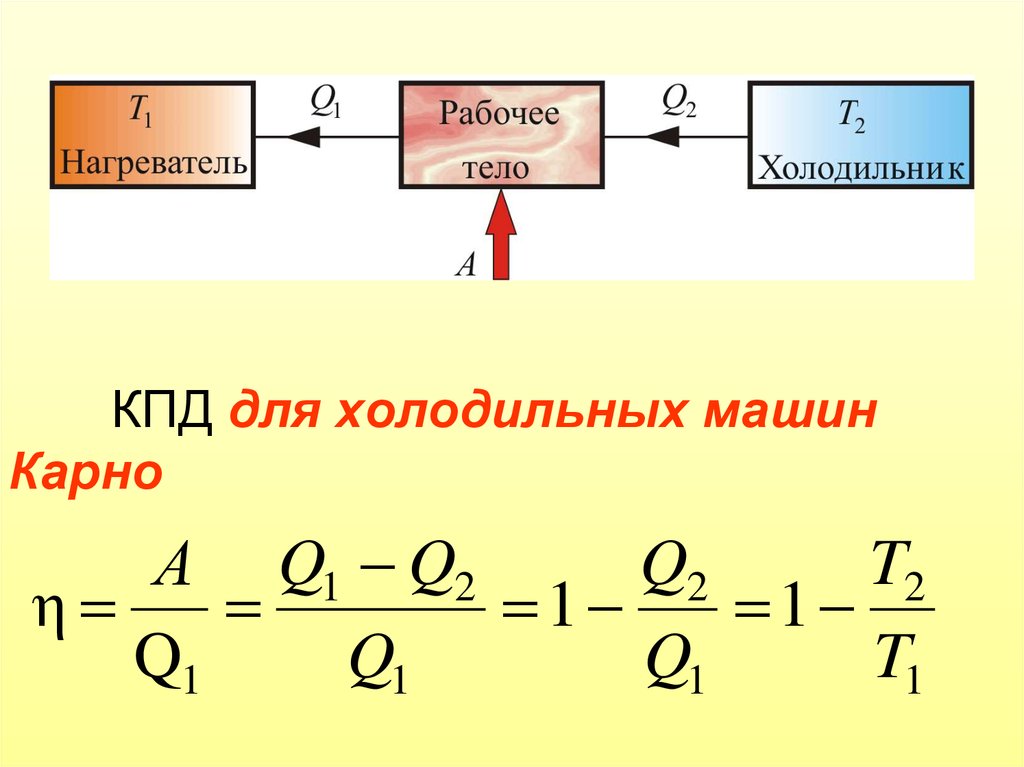

3. Что подавляющее большинство всех ныне известных цикличных «тепловых двигателей» (поршневых двигателей) работают по «разомкнутому циклу», когда после каждого цикла отработавшее свой цикл «рабочее тело» безжалостно выбрасывается. Пример – выброс выхлопных газов из двигателя внутреннего сгорания в атмосферу.

4. Что некоторые тепловые двигатели (например, турбореактивные самолётные и ракетные реактивные) вообще не работают циклично и поэтому пытаться пристегнуть к ним какой-нибудь «теоретический термодинамический цикл» – это явный признак отсутствия логики мышления или просто слабоумия.

5. Что никакому двигателю, работающему по «разомкнутому циклу» или работающему вообще не по циклу никакой «холодильник», вопреки уверениям горе-физико-теоретиков, не нужен. Так как «движущая сила в этих двигателях возникает не из-за разности температур, как нас пытаются убедить горе-физико-теоретики, а из-за разности давлений, в частности, в поршневых двигателях – из-за разницы давлений газов по разные стороны поршня, в турбинах – из-за разницы давлений газов по разные стороны рабочих лопаток турбины, в ракетных реактивных – из-за разницы давлений внутри и снаружи камеры сгорания.

6. Что существует лишь один тип поршневых двигателей, в которых реализован замкнутый цикл – это двигатели Стирлинга.

Так почему бы не начать изучать в школах вместо фантазийных циклов Карно реальные циклы, по которым работают реальные двигатели, а также их устройство и принципы работы. Если так интересен замкнутый цикл, то давайте будем рассматривать двигатели Стирлинга – их устройство, принцип работы и их теоретический цикл. Очень интересно было бы в школах на уроках физики рассмотреть устройство и принципы работы «огневого двигателя» «Друг рудокопа» капитана шахтёров Томаса Сэвери (Fire engine “Miner’s Friend”) и поршневого двигателя Томаса Ньюкомена. Чем в лучшую сторон отличались двигатели, которые начали изготавливать Джеймс Уатт и Мэттью Болтон? Каковы основные принципы работы (создания «движущей силы») у современных автомобильных двигателей, турбореактивных двигателей, ракетных реактивных двигателей?

Но открываешь «умную книжку»*, написанную Дирком тер Хааром (Dirk ter Haar), профессором теоретической физики в Оксфордском университете и Харальдом Вергеландом (Harald Nicolai Storm Wergeland), профессором Норвежского технологического института в Трондхэйме, и у меня последние волосы встают дыбом от некоторых профессорских мыслей:

*(D. ter Haar and H.N.S. Wergeland, Elements of Thermodynamics, Addison-Wesley, 1966, в русском переводе Д. Тер Хаар, Г. Вергеланд; Пер. с англ. И.Б. Виханского; Под ред. Н.М. Плакиды. — Москва : Мир, 1968.)

и затем:

Разумеется, нормальные инженеры в нормальной теплоэнергетике используют другие процессы, так как цикл Карно невозможно реализовать.

Но дальше что такое было? Новая идея насчёт «кубатуры круга»? Но уже применительно к теоретической термодинамике? Дорогие профессора, если бы вы были еще живы, я бы вам рассказал, чем закончились все попытки учёных создать кубатуру круга.

И почему, на каком основании сделан глобальный вывод о том, что «нет необходимости рассматривать другие циклы, как бы они не были важны для практических целей«? Это что, первые признаки начала старческого слабоумия? Или просто горе от ума?

Читая подобные «умные книжки», хочется повторить слова Альберта Эйнштейна, который, несмотря на то, что создал «теорию», в которой второй постулат опровергает первый, а конечным результатом «теории» является гениальная формула 1+1=1, всё же иногда говорил толковые вещи. Я только слегка подправлю слова Эйнштейна: «Бесконечны лишь Вселенная и глупость профессорская, при этом относительно бесконечности первой из них у меня имеются сомнения.»

После изучения теоремы Карно, которая гласит: «КПД цикла Карно определяется лишь температурами нагревателя и холодильника и не зависит от устройства двигателя и природы используемого в нем рабочего тела.» (цитата по учебнику С.В. Громов. «Физика. Оптика, тепловые явления, строение и свойства вещества.» Учебник для 11 класса общеобразовательных учреждений. Под редакцией Н.В. Шароновой. Допущено Министерством образования Российской Федерации. 6-е издание. Москва, «Просвещение», 2005) у школьников (и у студентов) чаще всего возникает представление, что КПД любого реально работающего теплового двигателя не зависит ни от устройства двигателя, ни от природы используемого в них рабочего тела.

Чиновники из Министерства просвещения, вы думаете, я ошибаюсь? Проведите опрос среди школьников выпускных классов и студентов технических вузов. Только не надо устраивать опрос в виде ЕГЭ, вопросников с несколькими ответами, среди которых есть один правильный. Мы не на выборах Путина. Вы просто дайте задание письменно ответить на вопросы – «напишите формулировку теоремы Карно» и «от чего зависит о от чего не зависит КПД обычного автомобильного двигателя внутреннего сгорания?».

В качестве помощи школьникам и студентам, а также многим школьным учителям физики, которые, судя по всему, тоже неверно представляют себе истинный смысл теоремы Карно, предлагаю решить следующую задачу.

Предположим, что нам необходимо при помощи идеального теплового двигателя выполнить некоторую полезную работу по подъему некоего груза массой m на высоту H (см. рис. 2А). То есть поднять груз из положения cd в поожение gh. В принципе, в самом начале своего существования основная работа, которая взваливалась «на плечи», а, вернее сказать, на коромысла «коромыслового огневого двигателя Ньюкомена» (Lever Fire Engine), в течение длительного времени, больше столетия, состояла только в том, чтобы поднимать (откачивать) воду из шахт. А КПД этих двигателей оценивалось показателем “duty”, дьюти, «количество футо-фунтов воды, которые поднимал двигатель при сжигании в топке двигателя одного бушеля самого качественного ньюкасльского угля».

Рис. 2. Расчётная схема для определения требуемого количества теплоты для выполнения различными реальными газами одинаковой работы по подъему груза.

Условимся, что работу будем выполнять, используя в качестве рабочего тела различные реально существующие в природе газы, а не виртуальный идеальный газ Gi (Gaz idéal) и исключительно за счет передачи рабочему телу тепловой энергии.

В положении cd груз находится в равновесии (см. рис. 2В). Уравнение равновесия для груза можно представить так:

G + p_атм. S = p_cd S [1], где:

G – вес груза,

p_атм. – величина атмосферного давления,

p_cd – давление газа, заключенного в сосуде abcd,

S – площадь поршня.

Чтобы при помощи идеального теплового двигателя выполнить работу по подъему груза, мы поставим «холодный» двигатель на нагреватель (тело A, имеющее температуру T_A), см. рис. 2С. Именно нагреватель, так как это тело A будет использоваться нами именно в этом качестве – оно будет нагревать «холодное» рабочее тело внутри двигателя с температурой T_cd < T_A.

Так как температура нагревателя выше температуры рабочего тела, то будет иметь место процесс теплообмена. Тело A, имеющее температуру T_A, будет передавать теплоту (тепловую энергию, внутреннюю энергию) рабочему телу идеального двигателя, имеющего более низкую температуру T_cd. Температура рабочего тела начнет повышаться, что вызовет увеличение давления внутри цилиндра (в полном соответствии с законом Шарля, который иногда называют вторым законом Гей-Люссака, P/ T = const), и поршень идеального теплового двигателя начнет двигаться вверх, выполняя работу по подъему груза. Допустим, что именно в тот момент, когда поршень достиг положения gh, температура рабочего тела идеального двигателя T_gh сравнялась с температурой нагревателя T_A (см. рис. 2D):

T_gh = T_A

Уравнение равновесия груза в этом положение будет описываться уравнением:

G + p_атм. S = p_gh S [2]

Из сравнения уравнений [1] и [2], следует вывод, что p_cd = p_gh То есть во время подъема давление внутри идеального рабочего двигателя практически не меняется. А это значит, что весь процесс подъема груза происходит при изобарном расширении газа, выступающего в роли рабочего тела.

Предположим, что в качестве рабочего тела мы поочередно использовали 1 моль каждого газа, приведенного в таблице 1. Предположим, что первоначальная температура рабочего тела Т_cd = 400 K, конечная Т_gh = 600 K. Смотрим таблицу 1.

Таблица 1.

Удельная и молярная изобарная теплоемкость газов при давлении 0,1 МПа,

а также количество теплоты, необходимой для выполнения одной и той же работы по подъёму грузов для оценки использования этих газов в качестве рабочего тела идеальной тепловой машины.

Из последней колонки таблицы 1 видно, что для выполнения одной и той же работы при использовании в качестве рабочего тела идеального теплового двигателя разных газов, необходимо передать рабочему телу совершенно разное количество теплоты. Причем существенно разное.

Так, наиболее экономичными являются аргон и неон – им на выполнение работы требуется около 4,16 кДж тепловой энергии, (а, вернее, 0,99 килокалории теплоты), азот, кислород и водород, с показателями от 5,84 до 6,22 кДж тепловой энергии занимают места в середничках, весьма неэффективны водяной пар и углекислый газ, а абсолютный рекордсмен по растранжириванию тепла – хлор – 12,74 кДж. То есть, для выполнения той же самой работы «хлорному» идеальному тепловому двигателю надо передать в три раза больше тепла, чем «аргонному» или «неонному».

Надеюсь, я наглядно продемонстрировал, что КПД теплового двигателя весьма существенно зависит от природы рабочего тела?

Теперь дело за Министерством просвещения – менять ли им школьные программы обучения и переписывать ли школьные учебники по физике или оставить всё «как есть», потому что… а зачем? Чиновников из Минпросвещения и самого министра и так неплохо кормят.

Кстати, школьники и студенты могут предложить своим педагогам решить подобную задачу с конкретными размерами цилиндров и поршней – и прислать решения вместе с расчётами мне. Я опубликую задачи и решения на своём канале.

Второй закон термодинамики в новой редакции — College Physics: OpenStax

Глава 15 Термодинамика

Резюме

  • Определение цикла Карно.
  • Рассчитайте максимальный теоретический КПД ядерного реактора.
  • Объясните, как диссипативные процессы влияют на идеальную машину Карно.

Рисунок 1. Эта новая игрушка, известная как пьющая птица, является примером двигателя Карно. Он содержит хлористый метилен (смешанный с красителем) в брюшной полости, который кипит при очень низкой температуре — около 100ºF . Для работы нужно намочить голову птицы. Когда вода испаряется, жидкость поднимается в голову, заставляя птицу утяжеляться и нырять вперед обратно в воду. Это охлаждает хлористый метилен в голове, и он перемещается обратно в брюшную полость, в результате чего низ птицы становится тяжелым, и она опрокидывается вверх. Если не считать очень небольшого вклада энергии — первоначального смачивания головы — птица становится своего рода вечным двигателем. (кредит: Arabesk.nl, Wikimedia Commons)

Из второго закона термодинамики мы знаем, что тепловая машина не может быть на 100 % эффективнее, поскольку всегда должна существовать некоторая теплопередача[латекс]\boldsymbol{Q _{\textbf{c} }}[/latex]в окружающую среду, которую часто называют отходящим теплом. Насколько эффективной может быть тепловая машина? На этот вопрос на теоретическом уровне ответил в 1824 г. молодой французский инженер Сади Карно (179 г.6–1832), в своем исследовании появившейся тогда технологии теплового двигателя, имеющей решающее значение для промышленной революции. Он разработал теоретический цикл, который теперь называется циклом Карно , который является наиболее эффективным из возможных циклических процессов. Второй закон термодинамики можно переформулировать в терминах цикла Карно, и, таким образом, Карно на самом деле открыл этот фундаментальный закон. Любая тепловая машина, использующая цикл Карно, называется двигателем Карно .

Важнейшее значение цикла Карно — и, по сути, его определение — заключается в том, что используются только обратимые процессы. Необратимые процессы связаны с диссипативными факторами, такими как трение и турбулентность. Это увеличивает передачу тепла[латекс]\boldsymbol{Q_{\textbf{c}}}[/латекс]в окружающую среду и снижает эффективность двигателя. Очевидно, что обратимые процессы предпочтительнее.

ДВИГАТЕЛЬ КАРНО

Сформулированный в терминах обратимых процессов, второй закон термодинамики имеет третью форму:

Двигатель Карно, работающий между двумя заданными температурами, имеет максимально возможный КПД любой тепловой машины, работающей между этими двумя температурами. Кроме того, все двигатели, использующие только обратимые процессы, имеют одинаковую максимальную эффективность при работе в пределах одних и тех же заданных температур.

На рис. 2 показана диаграмма[latex]\boldsymbol{PV}[/latex]для цикла Карно. Цикл включает два изотермических и два адиабатических процесса. Напомним, что и изотермические, и адиабатические процессы в принципе обратимы.

Карно также определил КПД идеальной тепловой машины, то есть машины Карно. Всегда верно, что КПД циклической тепловой машины определяется выражением:

.

[латекс]\boldsymbol{Эфф\:=}[/латекс][латекс]\boldsymbol{\frac{Q _{\textbf{h}} -Q _{\textbf{c}}}{Q _{\textbf{h }}}}[/латекс][латекс]\boldsymbol{=1-}[/латекс][латекс]\boldsymbol{\frac{Q_{\textbf{c}}}{Q_{\textbf{h}}} }.[/латекс]

Карно обнаружил, что для идеальной тепловой машины отношение[latex]\boldsymbol{Q_{\textbf{c}}/Q_{\textbf{h}}}[/latex] равно отношению абсолютных температур тепловые резервуары. То есть [латекс]\boldsymbol{Q_{\textbf{c}}/Q_{\textbf{h}}=T_{\textbf{c}}/T_{\textbf{h}}}[/latex]для двигатель Карно, так что максимум или Эффективность Карно [латекс]\boldsymbol{Eff _{\textbf{C}}}[/латекс] определяется как

[латекс]\boldsymbol{Eff _{\textbf{C}}=1-}[/latex][латекс]\boldsymbol{\frac{T_{\textbf{c}}}{T_{\textbf{h}} }},[/латекс]

, где[latex]\boldsymbol{T_{\textbf{h}}}[/latex]и[latex]\boldsymbol{T_{\textbf{c}}}[/latex]в градусах Кельвина (или любая другая абсолютная температура шкала). Ни одна настоящая тепловая машина не может работать так же хорошо, как КПД Карно — фактический КПД около 0,7 от этого максимума обычно является лучшим, чего можно достичь. Но идеальный двигатель Карно, как и пьющая птица выше, хотя и является увлекательной новинкой, но имеет нулевую мощность. Это делает его нереальным для любых приложений.

Интересный результат Карно подразумевает, что 100% эффективность была бы возможна только в том случае, если[latex]\boldsymbol{T_{\textbf{c}}=0\textbf{K}}[/latex]—то есть, только если бы холодный резервуар был при абсолютном нуле, практическая и теоретическая невозможность. Но физический смысл таков: единственный способ заставить всю теплопередачу пойти на работу — это убрать всю тепловую энергию, а для этого требуется холодный резервуар при абсолютном нуле.

Также очевидно, что наибольшая эффективность достигается, когда соотношение [латекс]\жирный символ{Т_{\textbf{с}}/Т_{\текстbf{h}}}[/латекс] является как можно меньшим. Как обсуждалось для цикла Отто в предыдущем разделе, это означает, что эффективность максимальна при максимально возможной температуре горячего резервуара и минимально возможной температуре холодного резервуара. (Эта установка увеличивает площадь внутри замкнутого контура на диаграмме [латекс]\boldsymbol{PV}[/латекс]; кроме того, кажется разумным, что чем больше разница температур, тем легче направить теплопередачу на работу. ) Фактические температуры резервуара тепловой машины обычно связаны с типом источника тепла и температурой окружающей среды, в которую происходит передача тепла. Рассмотрим следующий пример.

Рис. 2. PV диаграмма цикла Карно, использующего только обратимые изотермические и адиабатические процессы. Теплопередача Q h происходит в рабочее тело на изотермическом пути AB, который протекает при постоянной температуре Th. Теплообмен Q c происходит вне рабочего тела по изотермическому пути CD, который происходит при постоянной температуре T с . Чистый результат работы W равен площади внутри пути ABCDA. Также показана схема двигателя Карно, работающего между горячим и холодным резервуарами при температурах T h и T c . Любая тепловая машина, использующая обратимые процессы и работающая между этими двумя температурами, будет иметь такой же максимальный КПД, как и машина Карно.

Пример 1: Максимальная теоретическая эффективность ядерного реактора 9{\circ}\textbf{C}}[/latex], а затем снова нагревают, чтобы начать цикл заново. Рассчитайте максимальный теоретический КПД тепловой машины, работающей между этими двумя температурами.

Рисунок 3. Схематическая диаграмма ядерного реактора с водой под давлением и паровых турбин, преобразующих работу в электрическую энергию. Теплообмен используется для производства пара, отчасти для того, чтобы избежать загрязнения генераторов радиоактивностью. Две турбины используются, потому что это дешевле, чем работа одного генератора, который производит такое же количество электроэнергии. Пар конденсируется в жидкость перед возвратом в теплообменник, чтобы поддерживать низкое давление пара на выходе и способствовать прохождению пара через турбины (эквивалентно использованию холодного резервуара с более низкой температурой). Значительная энергия, связанная с конденсацией, должна рассеиваться в окружающей среде; в этом примере используется градирня, поэтому прямая передача тепла в водную среду отсутствует. (Обратите внимание, что вода, поступающая в градирню, не контактирует с паром, проходящим через турбины.) 9{\circ}\textbf{C}},[/latex] соответственно. Тогда в кельвинах [латекс]\boldsymbol{T_{\textbf{h}}=573\textbf{K}}[/latex]и[латекс]\boldsymbol{T_{\textbf{c}}=300\textbf { K}},[/latex], так что максимальная эффективность равна

[латекс]\boldsymbol{Eff _{\textbf{C}}=1-}[/latex][латекс]\boldsymbol{\frac{T_{ \textbf{c}}}{T_{\textbf{h}}}}.[/latex]

Таким образом,

[латекс]\begin{array}{lcl} \boldsymbol{Eff_{\textbf{C} }} & \boldsymbol{=} & \boldsymbol{1-\frac{300\textbf{ K}}{573\textbf{ K}}} \\ {} & \boldsymbol{=} & \boldsymbol{0. 476\textbf {, или }47,6\%.} \end{массив}[/latex]

Обсуждение

Фактический КПД типичной атомной электростанции составляет около 35%, что немногим лучше, чем 0,7 раза от максимально возможного значения, что является данью превосходной инженерной мысли. Электростанции, работающие на угле, нефти и природном газе, имеют больший фактический КПД (около 42%), потому что их котлы могут достигать более высоких температур и давлений. Температура холодного резервуара на любой из этих электростанций ограничена местными условиями. На рис. 4 показан (а) внешний вид атомной электростанции и (б) внешний вид угольной электростанции. У обоих есть градирни, в которые вода из конденсатора поступает в градирню в верхней части и распыляется вниз, охлаждаясь за счет испарения.

Рисунок 4. (а) Атомная электростанция (фото: BlatantWorld.com) и (б) угольная электростанция. Оба имеют градирни, в которых вода испаряется в окружающую среду, представляя Q c . Ядерный реактор, поставляющий Q h , расположен внутри куполообразной защитной оболочки. (Фото: Роберт и Михаэла Викол, publicphoto.org)

Поскольку все реальные процессы необратимы, реальный КПД тепловой машины никогда не может быть таким же большим, как у двигателя Карно, как показано на рис. 5(а). Даже при наличии наилучшей тепловой машины в периферийном оборудовании, таком как электрические трансформаторы или автомобильные трансмиссии, всегда присутствуют диссипативные процессы. Это еще больше снижает общую эффективность за счет преобразования части выходной мощности двигателя обратно в теплопередачу, как показано на рис. 5(b).

Рис. 5. Реальные тепловые двигатели менее эффективны, чем двигатели Карно. (а) В реальных двигателях используются необратимые процессы, уменьшающие передачу тепла на работу. Сплошные линии представляют реальный процесс; пунктирные линии — это то, что двигатель Карно сделал бы между теми же двумя резервуарами. б) Трение и другие диссипативные процессы в выходных механизмах тепловой машины преобразуют часть ее работы в теплопередачу окружающей среде.

  • Цикл Карно — это теоретический цикл, который является наиболее эффективным из возможных циклических процессов. Любой двигатель, использующий цикл Карно, в котором используются только обратимые процессы (адиабатический и изотермический), известен как двигатель Карно.
  • Любой двигатель, использующий цикл Карно, обладает максимальным теоретическим КПД.
  • Хотя двигатели Карно являются идеальными двигателями, в действительности ни один двигатель не достигает теоретического максимального КПД Карно, поскольку определенную роль играют диссипативные процессы, такие как трение. Циклы Карно без потери тепла могут быть возможны при абсолютном нуле, но это никогда не наблюдалось в природе.

 

Цикл Карно
циклический процесс, в котором используются только обратимые процессы, адиабатические и изотермические процессы
Двигатель Карно
тепловой двигатель, использующий цикл Карно
Эффективность Карно
максимальный теоретический КПД тепловой машины

 

6.

2: Двигатели и тепловая эффективность

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    18480
    • Том Вайдеман
    • Калифорнийский университет в Дэвисе

    Простой двигатель

    Циклические процессы позволяют иметь повторяющиеся способы преобразования тепловой энергии, поступающей в газ, в рабочую энергию, выходящую из газа. Мы знаем, что для теплообмена должна существовать разница температур, и правильно спроектированное устройство может работать в цикле, чтобы использовать разницу температур для получения полезной механической энергии. Такое устройство называется тепловая машина . Конечно, для этого требуется циклический процесс, который проходит по часовой стрелке на диаграмме \(PV\). Теперь мы рассмотрим простейший вариант двигателя, который образует прямоугольник на своей диаграмме \(PV\). Мы будем делать акцент на том, чтобы визуализировать каждый этап цикла как физический процесс, в котором поршень обменивается теплом с тепловым резервуаром и/или взаимодействует с окружающей средой.

    Рисунок 6.2.1 – Простой двигатель

    Начнем с того, что мы уже знаем о циклах: поскольку термодинамическое состояние возвращается к исходному состоянию, внутренняя энергия не меняется в течение цикла, а это означает, что рабочая энергия, на выходе (равном площади, заключенной в петле) равна тепловой энергии, поступающей внутрь.

    \[\Delta U = 0\;\;\;\Rightarrow\;\;\; Q_{in} = W_{out} = \left(P_2-P_1\right)\left(V_2-V_1\right) \]

    Теперь мы вычислим тепло, переданное во время всех четырех отдельных этапов циклического процесса, чтобы подтвердить этот результат. При этом мы будем включать диаграмму того, что происходит физически.

    Рисунок 6.2.2a – Процесс A–B

    термальный резервуар это чуть теплее, чем газ в двигателе на каждом этапе процесса). Температура газа в процессе повышается, а объем увеличивается, при этом в систему поступает тепло. Количество переданного тепла:

    \[Q_{AB} = nC_P\Delta T_{AB} = nC_P\left(\dfrac{P_2\Delta V_{AB}}{nR}\right)=\left(\dfrac{C_P}{R}P_2 \right)\left(V_2-V_1\right) \]

    изохорный процесс и так как давление падает, это должно быть потому, что температура падает. Это может происходить только при неизменном объеме, когда тепло уходит из системы, а так как процесс квазистатический, то температура теплового резервуара на протяжении всего процесса несколько ниже температуры газа. Потеря тепла на этом этапе составляет:

    \[Q_{BC} = nC_V\Delta T_{BC} = nC_V\left(\dfrac{\Delta P_{BC}V_2}{nR}\right)=\left(\dfrac{C_V}{R} V_2\right)\left(P_1-P_2\right) \]

    нога снова изобарический процесс , на этот раз с падением температуры и объема. Опять же, этот квазистатический процесс требует, чтобы температура резервуара оставалась немного ниже температуры газа. Потери тепла:

    \[Q_{CD} = nC_P\Delta T_{CD} = nC_P\left(\dfrac{P_2\Delta V_{CD}}{nR}\right)=\left(\dfrac{C_P}{R} P_1\right)\left(V_1-V_2\right) \]

    температура за счет тепла, подведенного из термального резервуара, немного выше температуры газа. Передаваемое тепло:

    \[Q_{DA} = nC_V\Delta T_{DA} = nC_V\left(\dfrac{\Delta P_{DA}V_1}{nR}\right)=\left(\dfrac{ C_V}{R}V_1\справа)\слева(P_2-P_1\справа) \]

    Читателю предлагается в качестве упражнения по алгебре продемонстрировать, что сумма этих четырех теплопередач равна общей теплопередаче, как указано в уравнении 6.2.1. При выполнении этого упражнения будет полезно помнить, что \(C_P = C_V + R\).

    Двигатели реального мира

    В ходе приведенных выше расчетов читателю могло прийти в голову, что постоянно возникало одно неудобное требование — тепловой резервуар всегда должен иметь бесконечно малую величину, отличную от температуры газа в двигателе. Как именно человек совершает такой подвиг? Резервуар становится немного теплее, увеличивая температуру газа до тех пор, пока они не придут к тепловому равновесию, затем резервуар снова становится немного теплее, так что он снова может отдавать небольшое количество тепла газу, и так далее? Этот процесс, очевидно, не может быть разумно сконструирован, и даже если бы это было возможно, тот факт, что скорость теплового потока связана с разницей температур, означает, что он будет мучительно медленным.

    В реальном мире у нас обычно есть два термальных резервуара с фиксированными температурами для работы: один с высокой температурой, от которого двигатель получает тепло, и один с низкой температурой, куда двигатель отводит тепло. Обратите внимание, что в приведенном выше простом двигателе газ должен был как получать, так и отдавать тепло, даже если он получил чистое количество тепла, которое он преобразовал в работу. Это оказывается необходимой характеристикой всех двигателей (по причинам, которые мы рассмотрим позже) — двигатель не может просто брать тепло из одного горячего теплового резервуара и преобразовывать его в работу в цикле, не отдавая при этом тепло в другой. , более холодный термальный резервуар. Схема этого общего принципа двигателей показана ниже. 9Рисунок 6.2.3 – Реальная схема теплового двигателя Во-первых, процесс должен быть циклическим, что означает, что общее изменение внутренней энергии равно нулю, а общее поступающее тепло (тепло, поступающее из более теплого резервуара за вычетом тепла, отводимого в более холодный резервуар) равняется полной работе, которую необходимо совершить. выходит (технически есть еще работа, которая приходит, но эта схема включает только net работают, при этом отделяя «входящее» тепло от «исходящего» по причинам, которые скоро станут ясны). Мы включили теплоты, обмениваемые с двумя резервуарами, в терминах их абсолютных значений, так что нам не нужно заботиться о условном обозначении подвода/отвода тепла. Ясно, что произведенная работа представляет собой разность общей тепловой энергии, поступающей из горячего резервуара, за вычетом общей тепловой энергии, отводимой в холодный тепловой резервуар.

    Тепловая эффективность

    Это правда, что в реальном мире когда мы берем тепло из одного резервуара и отдаем его в другой, более холодный, мы делаем два резервуара немного ближе по температуре. В идеале мы хотели бы избежать «траты впустую» любой из этой исходящей тепловой энергии, которая не делает ничего, кроме повышения температуры более холодного резервуара, а вместо этого просто преобразовать всю тепловую энергию, поступающую из горячего резервуара, непосредственно в работу. Достижение этой цели означало бы создание «совершенно эффективного двигателя», и мы бы сказали, что он имеет тепловой КПД 100%. Таким образом, определение процентной эффективности любого двигателя довольно очевидно — просто возьмите отношение извлекаемой работы к подведенному теплу:

    \[ e = \dfrac{W_{net}}{Q_H} = \dfrac{\left|Q_H \right|-\left|Q_C\right|}{\left|Q_H\right|} = 1 — \dfrac{\left|Q_C\right|}{\left|Q_H\right|}\]

    Должно следует отметить, что «извлеченная работа» — это чистая работа — работа, которая выходит в течение полного цикла, за вычетом вложенной работы (т. е. это площадь внутри замкнутого контура на PV-диаграмме по часовой стрелке). Заметьте также, что для этого двигателя температура не просто немного выше температуры газа в двигателе, и на самом деле сила, вызванная давлением газа, ненамного больше, чем внешняя сила, когда совершается работа. Таким образом, ни один из этих процессов не является квазистатическим. Но, как мы видели, это не помешает нам эффективно использовать модели квазистатических процессов.

    Позже мы увидим, что двигатели максимально эффективны, когда процессы, за которыми они следуют, обратимы, но, конечно, для некоторых процессов это требует, чтобы задействованный тепловой резервуар изменял свою температуру, чтобы оставаться бесконечно мало больше или меньше, чем температура двигателя. Это противоречит самому понятию «теплового резервуара», поэтому ясно, что реальный КПД двигателя будет хуже, чем у реверсивных двигателей, которые мы можем использовать для их моделирования. Тем не менее, мы можем использовать отношение общей работы к общему теплу для обратимой модели, чтобы вычислить максимальная возможная эффективность для смоделированного двигателя.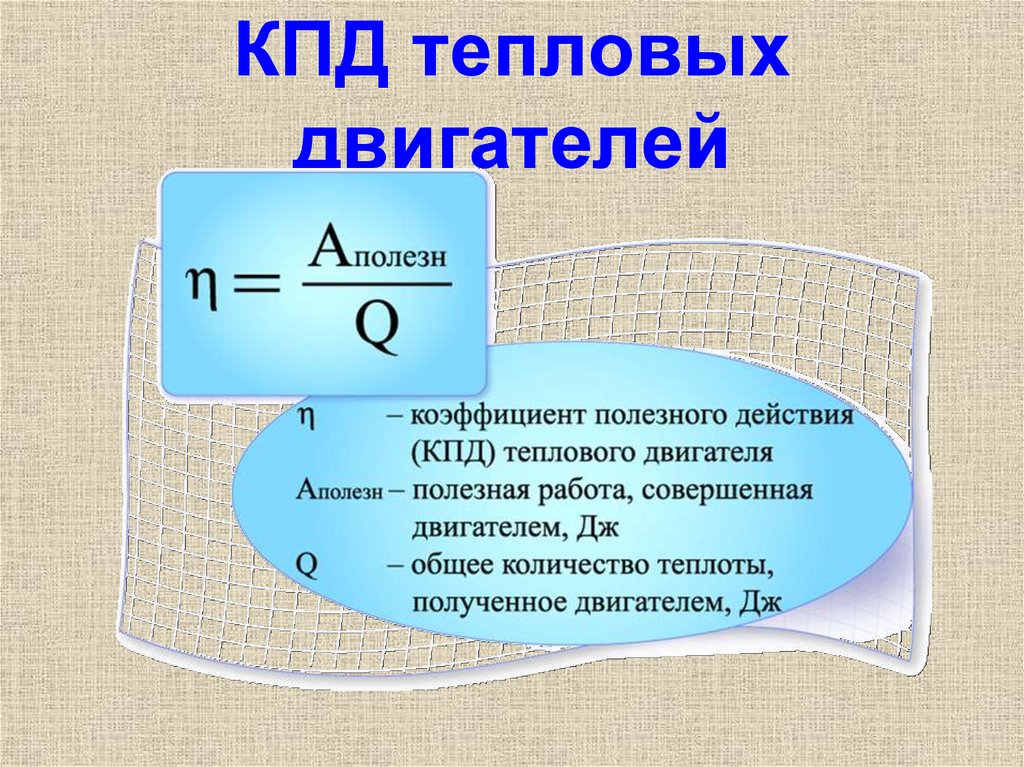

      Пример \(\PageIndex{1}\)

      В циклическом процессе для двигателя, показанного ниже, процесс от A до B увеличивает давление втрое, процесс от B до C является адиабатическим, а рабочий газ в двигатель одноатомный. Вычислите максимальный тепловой КПД этого двигателя.

      Раствор

      Обозначим объем газа на изохорном участке (\(A\стрелка вправо B\)) \(V_o\). Мы можем использовать адиабатический процесс, чтобы связать объем, занимаемый газом в точке С, с \(V_o\): 9{\ frac {3} {5}}V_o \right)\right] = -0,933P_oV_o \end{массив}\right\}\;\;\;\Rightarrow\;\;\; W_{net}=W_1+W_2 = 0,667P_oV_o\номер\]

      Тепло уходит из системы во время изобарического процесса, а во время адиабатического процесса тепло не обменивается, поэтому все тепло, поступающее в двигатель, поступает во время изохорного процесса, и это легко вычислить для одноатомного идеального газа:

      \[Q_{in} = \frac{3}{2}\Delta P V = 3P_oV_o \nonnumber\]

      Эффективность определяется отношением чистой работы к теплу:

      \[e = \dfrac{W_{net}}{Q_{in}} = \dfrac{0,667P_oV_o}{3P_oV_o} = 22,2\% \nonnumber\]

       

      Цикл Отто

      Наш самый узнаваемый тип двигателя — это двигатель внутреннего сгорания, а наиболее распространенный циклический процесс, которому они следуют, называется Цикл Отто .

      Предупреждение

      В дальнейшем, когда слово «газ» относится к газу внутри поршня, который в основном представляет собой воздух. Говоря о бензине (наиболее распространенном топливе для сжигания топлива), мы будем называть его в этой длинной форме — мы не будем использовать сокращенную версию «газ».0343

      Мы начнем с того, что построим диаграмму \(PV\), которая аппроксимирует процесс, а затем объясним каждую часть цикла.

      Рисунок 6.2.4 – Цикл Отто

      Пары бензина (или другого горючего) попадают в камеру и смешиваются с воздухом при прохладной (окружающей) температуре, когда над смесью совершается работа по ее сжатию. Это происходит очень быстро, так что газ не успевает обмениваться теплом с окружающей средой, что и побуждает рассматривать этот процесс как адиабатический.

      процесс B-C (изохорный нагрев)

      Бензин воспламеняется, что приводит к быстрому изменению температуры газа внутри поршня. Технически тепло поступает не снаружи двигателя, а скорее в результате экзотермического химического процесса, но это одно и то же. Это воспламенение происходит очень внезапно, прежде чем газ успеет расширить поршень, поэтому мы рассматриваем этот процесс как изохорный.

      процесс C-D (адиабатическое расширение)

      Нагретый газ теперь находится под очень высоким давлением, и это давление расширяет поршень, совершая работу. Опять же, скорость этого процесса настолько велика, что очень мало тепла успевает выйти из поршня, когда он происходит, поэтому мы рассматриваем этот процесс как адиабатический.

      процесс D-A (изохорное охлаждение)

      После полного расширения охлажденный, но еще более горячий, чем окружающая среда газ выбрасывается из двигателя, и в камеру поступает новая порция воздуха и паров бензина. Технически газ не «охлаждается изохорически», но это равносильно тому, что камера вскоре заполняется новым газом с более низкой температурой и тем же объемом.

      Этот пример показывает, как мы можем использовать то, что мы узнали о термодинамических процессах, для анализа реальных ситуаций, даже если наше понимание основано на идеальных ситуациях, которых не существует в реальном мире. Мы просто смотрим на особенности реального процесса и максимально приближаем его к квазистатическому процессу. Во время этого процесса «сопоставления» мы заботимся о том, чтобы конечные точки совпадали правильно (поскольку это состояния равновесия) и чтобы тепло/работа, передаваемые во время процесса, имели смысл. В приведенном выше примере это состояло в том, чтобы спросить, произошел ли процесс быстро (нет времени для отвода тепла) или не изменился ли объем (нет выполненной работы). Вскоре мы снова увидим другую форму этого сопоставления.

      Давайте посмотрим на эффективность этого цикла. Имейте в виду, что наша идеализированная версия будет более эффективной, чем то, что мы можем достичь в реальном мире, но это дает нам верхний предел того, на что мы можем надеяться. Чтобы получить КПД, нам нужно тепло, отдаваемое горячим резервуаром, и тепло, забираемое холодным резервуаром. В этом цикле теплообмен происходит только во время процессов B-C и DA, которые оба являются изохорными, поэтому теплообмен пропорционален изменениям температуры. Таким образом, эффективность определяется выражением:

      \[e = 1 — \dfrac{\left|Q_C\right|}{\left|Q_H\right|} = 1 — \dfrac{nC_V\left(T_D — T_A\right)}{nC_V\left( T_C — T_B\right)} = 1 — \dfrac{\left(T_D — T_A\right)}{\left(T_C — T_B\right)} \]

      Из этого результата должно быть ясно, что двигатель работает больше эффективно, когда разница температур между двумя тепловыми резервуарами больше. В данном случае это разница между температурой впрыскиваемого газа и воспламененного газа. Из диаграммы должно быть ясно, что эта разница может быть измерена как разность (или, правильнее сказать, отношение) двух объемов, занимаемых газом. С практической точки зрения, газ нельзя сжать до минимального объема, прежде чем воспламенить его, потому что повышение температуры из-за сжатия само по себе может самопроизвольно воспламенить газ. Топливо с более высоким октановым числом обеспечивает большую степень сжатия без нежелательного самовоспламенения, что повышает эффективность.

      Как мы можем сделать вывод из вышеизложенного, КПД этого двигателя можно переписать в терминах переменной, которую нам легче измерить, чем температуры, а именно свойства самого двигателя. Два из четырех процессов являются изохорными, что означает, что объем изменяется только дважды в течение всего цикла, что означает, что нам нужно беспокоиться только о двух объемах — максимальном и минимальном. Максимум возникает при полном расширении поршня, а минимум при его полном сжатии. Нас даже не волнует, каковы эти значения, когда дело доходит до эффективности, а все, что нас волнует, это 9{1-\gamma}\]

      Цикл Дизеля

      Небольшим изменением цикла Отто можно несколько повысить КПД. Это изменение заключается в управлении процессом воспламенения таким образом, чтобы он происходил при постоянном давлении, а не при постоянном объеме. В этой конструкции двигателя используется так называемый дизельный цикл . Это, конечно, означает, что воспламенение должно происходить менее «взрывно», что снижает скорость, с которой может произойти цикл, и мы знаем из Физики 9А, что скорость, с которой производится работа, является мощностью цикла, поэтому, хотя это цикл получается более эффективным, он обеспечивает меньшую мощность.

      Чтобы определить разницу в КПД, нужно только изменить знаменатель уравнения 6.2.7, учитывающего процесс воспламенения (с B на C). Вместо того, чтобы происходить при постоянном объеме, это происходит при постоянном давлении, что просто изменяет \(C_V\) на \(C_P\), что дает:

      \[e = 1-\dfrac{C_V\left(T_D-T_A\ right)}{C_P\left(T_C-T_B\right)}=1-\dfrac{1}{\gamma}\;\dfrac{T_D-T_A}{T_C-T_B}\]

      Член, который вычитается из эффективность снижается на гамма-фактор, что приводит к более высокой эффективности. Кроме того, возможны более высокие степени сжатия, поскольку воздух сжимается без топлива (топливо добавляется постепенно, используя топливных форсунок в процессе воспламенения, поддерживая постоянное давление), устраняя проблему воспламенения топлива при сжатии. Конечно, хотя много лет назад этот процесс применялся исключительно для дизельных двигателей, в настоящее время впрыск топлива и сопровождающая его более высокая степень сжатия являются стандартом для автомобилей, работающих на бензине.

      Цикл Карно

      Мы смогли грамотно описать циклы Отто и Дизеля в терминах 4 квазистатических процессов, рассматривая воспламенение газа так, как если бы тепло добавлялось, а не в результате химической реакции, и рассматривая замещение газа, как будто выделяется тепло. Без этих приемов сохранение квазистатических процессов сделало бы их очень медленными и не могло бы происходить между резервуарами с двумя фиксированными температурами, как показано на рис. чтобы и изохорический, и изобарический процессы происходили квазистатически, температура резервуара должна изменяться таким образом, чтобы она лишь бесконечно мало отличалась от температуры газа. Мы не можем получить что-то даром, и на самом деле процессы воспламенения и замещения газа необратимы, что делает эти процессы лишь приблизительно квазистатическими циклами, которые мы объявили.

      Из этого анализа мы видим, что проблема с включением изохорных и изобарических процессов в «реальный» случай двигателя, вынужденного работать между двумя резервуарами с фиксированными температурами, заключается в том, что мы не можем сделать эти процессы обратимыми.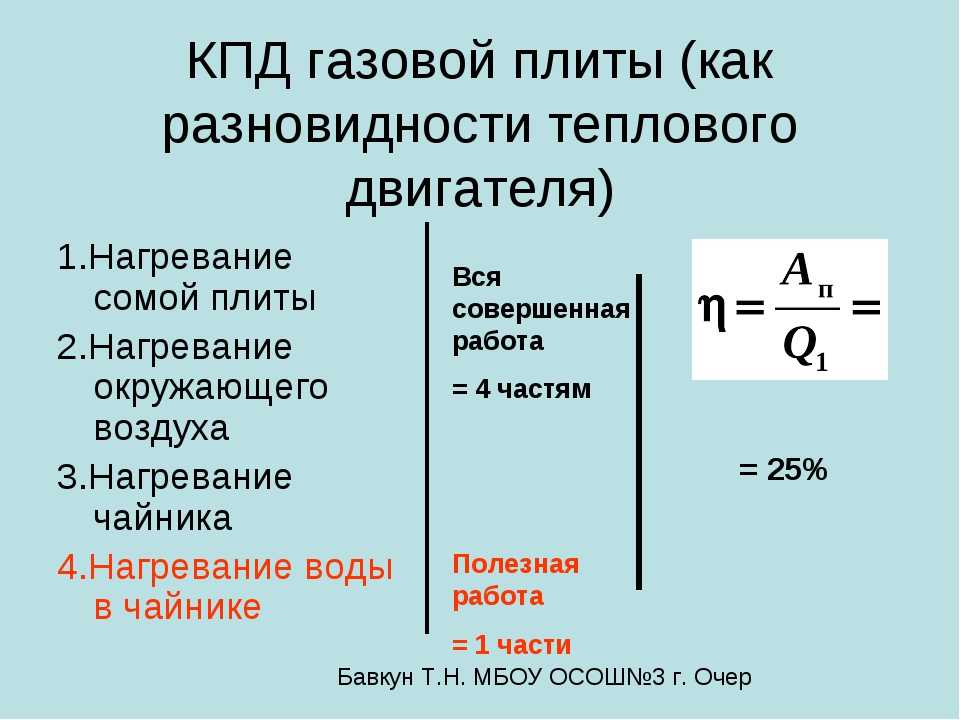 Но даже при этом фиксированном температурном ограничении резервуаров есть два процесса, которые мы можем (в принципе) выполнять квазистатически. Адиабатический процесс вообще не включает теплопередачу, поэтому относительная температура двигателя и резервуара не имеет значения. Изотермический процесс оставляет температуру двигателя неизменной, поэтому, если она равна температуре резервуара, проблем не возникает.

      В обсуждении, последовавшем за уравнением 5.8.20, мы отметили, что в любой данной точке на PV-диаграмме газа адиабата, проходящая через эту точку, круче, чем изотерма, которая также проходит через нее. Из-за этого мы можем создать циклический процесс, в котором используются два изотермических процесса (один вверху, один внизу диаграммы PV) и два адиабатических процесса (по одному на каждой стороне диаграммы PV), и этот цикл может быть приводимый в движение двумя резервуарами с фиксированной температурой. Это известно как Цикл Карно .

      Рисунок 6.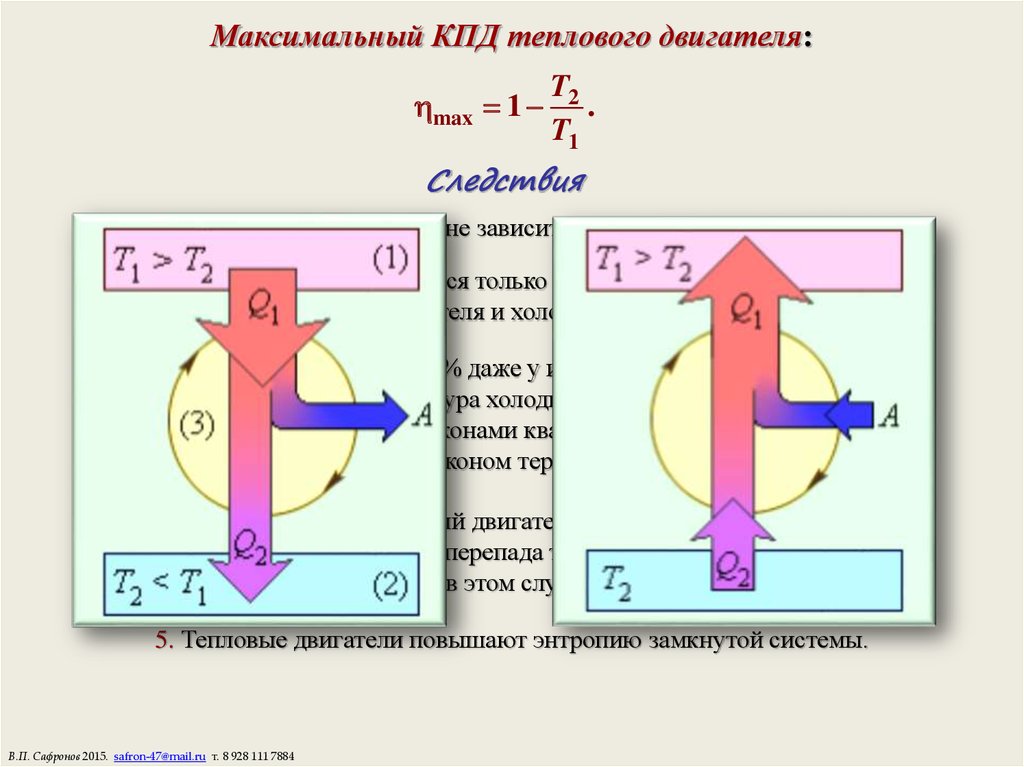 2.5 – Цикл Карно Отметив, что теплота не передается во время двух адиабатических процессов, и используя уравнение 5.8.16 для теплоты, переданной во время двух изотермических процессов, мы имеем:

      \[ \left. \begin{массив}{l} \left|Q_H\right| = W_{out} = nRT_H\ln\left[\dfrac{V_B}{V_A}\right] \\ \left|Q_C\right| = -W_{in} = -nRT_C\ln\left[\dfrac{V_D}{V_C}\right]=nRT_C\ln\left[\dfrac{V_C}{V_D}\right] \\ e = 1 — \ dfrac{\left|Q_C\right|}{\left|Q_H\right|} \end{массив} \right\} \;\;\;\Rightarrow\;\;\; e = 1-\dfrac{T_C}{T_H}\dfrac{\ln\left[\dfrac{V_C}{V_D}\right]}{\ln\left[\dfrac{V_B}{V_A}\right]} \] 9{\gamma-1} \end{массив} \right\} \;\;\;\Rightarrow\;\;\; \dfrac{V_B}{V_A} = \dfrac{V_C}{V_D}\]

      Подстановка их выше приводит к сокращению логарифмов в числителе и знаменателе, что делает эффективность цикла Карно простой функцией температур два резервуара:

      \[e=1-\dfrac{T_C}{T_H} \]

      Чем больше разница температур между двумя резервуарами, тем выше КПД двигателя Карно.

      Холодильники

      Одна вещь, которую мы постоянно видели в нашем обсуждении двигателей, это то, что циклы идут по часовой стрелке на диаграмме PV . Это гарантирует, что после полного цикла из системы выходит работы из , а тепла уходит из . Что произойдет, если мы запустим цикл в обратном порядке? Затем идет работа и уходит тепло. Это основа холодильника . Естественно, это не значит, что мы можем взять двигатель внутреннего сгорания, включить его «задним ходом», и он превратится в кондиционер. Во-первых, мы не можем «не воспламенить» газ. Но мы можем осуществлять процессы в обратном направлении другими средствами. Во-первых, давайте посмотрим на схему холодильника, как мы сделали это для тепловой машины:

      Рисунок 6.2.6 – Реальная схема холодильника здесь состоит в том, чтобы отвести как можно больше тепла от холодного резервуара, совершая при этом как можно меньше работы. Поэтому мы определяем коэффициент полезного действия как отношение отводимой теплоты к необходимой работе:

      \[K=\dfrac{\left|Q_C\right|}{W}=\dfrac{\left|Q_C\right|}{\left|Q_H\right|-\left|Q_C\right|}\ ]

      Чрезвычайно упрощенный способ представить себе, как работает холодильник, таков: мы знаем, что если мы очень резко сожмем газ, он станет намного горячее (см. пример в самом конце раздела 5.8). Неудивительно, что верно и обратное: резкое расширение поршня газом приводит к сильному охлаждению газа. Предположим, мы хотим, чтобы внутри холодильника было холоднее, чем снаружи (да, это определение холодильника!). Начните с газа в поршне вне холодильника, сожмите его до небольшого объема и подождите сжатым, пока он не достигнет температуры наружного воздуха. Затем резко отпустите поршень и быстро отнесите его в холодильник. Если мы сожмем его достаточно, изменение температуры газа в поршне сделает его температуру ниже температуры внутри холодильника. Подождем немного, пока внутренняя часть холодильника отдает тепло холодному воздуху в поршне, тем самым охлаждая воздух внутри холодильника. Когда они достигают равновесия, мы выносим поршень наружу и повторяем процесс. Это транспортирует тепловую энергию из холодильника.

      Работа, совершаемая газом при сжатии, превышает работу, совершаемую газом при расширении (т.е. необходимо приложить чистую работу). Процессы сжатия и расширения являются адиабатическими, а процессы «ожидания» — изохорными, поэтому PV-диаграмма выглядит примерно так:

      Очевидно, мы пожертвовали реальностью ради этого понятного «холодильника». Очевидно, что нам не нужно транспортировать поршень в охлаждаемую камеру и из нее, и вместо этого мы можем подавать газ в нее и из нее, сжимая его на выходе и расширяя на входе. Но есть еще довольно большая проблема с этой конструкцией. Для того чтобы тепло передавалось в нужных направлениях в нужные моменты времени, нам нужно, чтобы температура газа после его охлаждения от расширения была ниже температуры окружающей среды в холодильнике. PV температуры внутри и снаружи холодильников более или менее соответствуют температурам состояний B и D соответственно. Это означает, что если мы проводим изотермы через точки B и D , то разрыв между этими изотермами представляет собой максимальный температурный разрыв, который мы можем поддерживать между горячей и холодной областями. Очевидно, это зависит от разницы давлений, которую мы можем создать между сжатым газом и расширенным газом, но с практической точки зрения это является существенным препятствием.

      Это ограничение можно преодолеть, перенеся большую часть тепловой энергии в фазу хладагента. Мы знаем, что мы можем менять фазы, комбинируя сжатие/расширение и нагрев/охлаждение жидкости, а скрытая теплота парообразования значительна по сравнению с удельной теплоемкостью при небольшом изменении температуры. Это приводит к следующему основному процессу:

      • компрессор превращает хладагент в жидкую фазу, которая нагревает его выше температуры наружного воздуха
      • затем жидкость поступает в змеевик конденсатора , целью которого является увеличение площади контакта с наружным воздухом, ускорение процесса сброса тепла
      • к тому времени, когда жидкость прошла через змеевик конденсатора, она находится под высоким давлением, но пришла в термическое равновесие с наружным воздухом, и затем она проходит в расширительный клапан , где она адиабатически расширяется, изменяя фазу назад к газу и значительному падению температуры ниже температуры внутреннего воздуха
      • затем газ проходит через змеевик испарителя , что увеличивает скорость, с которой тепло может попасть в хладагент из внутреннего воздуха, и в конце змеевика испарителя он снова поступает в компрессор, чтобы снова запустить цикл.
    Posted inПопулярное