Содержание

8.4: Передаточное отношение

Передачи используются не только для передачи мощности, но также для обеспечения возможности настройки механического преимущества для механизма. Как обсуждалось во введении к данному блоку, в некоторых случаях электромотор сам по себе обладает достаточной мощностью для выполнения конкретной задачи, но выходные характеристики электромотора не соответствуют требованиям. Электромотор, который вращается ОЧЕНЬ быстро, но при очень малом крутящем моменте , не подходит для подъема тяжелого груза. В таких случаях возникает необходимость использования передаточного отношения для изменения выходных характеристик и создания баланса крутящего момента и скорости.

Представьте себе велосипед: велосипедист обладает ограниченной мощностью, и хочет обеспечить максимальное использование этой мощности в любой момент времени.

Путем изменения механического преимущества изменяется скорость движения. Мощность представляет собой количество проделанной работы в единицу времени. Чем больше количество работы. тем ниже скорость ее выполнения.

Пример 8.1

В примере 8.1 показано, что если на стороне входа рычаг сместится на 1 метр, на стороне выхода рычаг сместится на 4 метра. Разница пропорциональна соотношению между длинами рычагов.

Длина на выходе / Длина на входе = 8 / 2 = 4

Интересно то, что оба расстояния преодолеваются за одно и то же время. Давайте представим, что смещение рычага на входе на 1 метр происходит за 1 секунду, так что скорость движения на входе составляет 1 метр в секунду. В то же время, на выходе смещение на 4 метра также происходит за 1 секунду, так что скорость движения здесь составляет 8 метров в секунду. Скорость на выходе БОЛЬШЕ скорости на входе за счет соотношения между длинами рычагов.

Пример 8.2

В примере 8.2 представлена та же система, что и в примере 8.1, но теперь на вход действует сила, равная 4 ньютонам. Какова равнодействующая сила на выходе?

Прежде всего, необходимо рассчитать приложенный момент в центре вращения, вызванный входной силой, с помощью формул из Блока 7:

Крутящий момент = Сила х Расстояние от центра гравитации = 4 Н х 2 м = 8 Н-м

Далее, необходимо рассчитать равнодействующую силу на выходе:

Сила = Крутящий момент / Расстояние = 8 Н-м / 8 м = 1 ньютон

Глядя на эти два примера, мы видим, что если система смещается на 1 метр под действием входной силы, равной 4 ньютона, то на выходе она сместится на 4 метра под действием силы, равной 1 ньютон. При меньшей силе рычаг смещается быстрее!

Мы можем видеть, как механическое преимущество (выраженное в форме рычагов) может быть использовано для управления входной силой в целях получения требуемого выхода. Передачи работают по тому же принципу.

Цилиндрическая прямозубая шестерня по сути представляет собой серию рычагов. Чем больше диаметр шестерни, тем длиннее рычаг.

Пример 8.3

Как видно из примера 8.3, результатом крутящего момента, приложенного к первой шестерне, является линейная сила, возникающая на кончиках ее зубьев. Эта же сила воздействует на кончики зубьев шестерни, с которой зацепляется первая шестерня, заставляя вторую вращаться по действием крутящего момента. Диаметры шестерен становятся длиной рычагов, при этом изменение крутящего момента равносильно соотношению диаметров. Если малые шестерни приводят в движение больше шестерни, крутящий момент увеличивается. Если большие шестерни приводят в движение малые шестерни, крутящий момент уменьшается.

Пример 8.4

В примере 8.4, если входная 36-зубая шестерня поворачивается на расстояние одного зуба (d = ширина 1 зуба), это означает, что она поворачивается на 1/36-ю своего полного оборота (а1 = 360 / 36 = 10 градусов). Поворачиваясь, она приводит в движение 60-зубую шестерню, заставляя последнюю смещаться также на 1 зуб. Тем не менее, для 60-зубой шестерни это означает смещение всего лишь на 1/60-ю полного оборота (а2 = 360 / 60 = 6 градусов).

Когда малая шестерня проходит определенное расстояние в заданный интервал времени, большая шестерня при этом проходить меньшее расстояние. Это означает, что большая шестерня вращается медленнее малой. Этот принцип работает в обоих направлениях. Если малые шестерни приводят в движение больше шестерни, скорость понижается. Если большие шестерни приводят в движение малые шестерни, скорость повышается.

Из примеров 8.1 — 8.4 видно, что отношение между размерами двух зацепляющихся между собой шестерен пропорционально изменению крутящего момента и скорости между ними. Это называется передаточным числом.

Как обсуждалось выше, количество зубьев шестерни прямо пропорционально ее диаметру, поэтому для расчета передаточного отношения вместо диаметра можно просто считать зубья.

Передаточное отношение выражается как (зубья ведущей шестерни) : (зубья ведомой шестерни), поэтому представленная выше пара шестерен может быть описана как 12:60 (или 36 к 60).

Передаточное число рассчитывается по формуле (зубья ведомой шестерни) / (зубья ведущей шестерни)

Поэтому передаточное число = зубья ведомой шестерни / зубья ведущей шестерни = 60/36 = 1,67


 

Как обсуждалось выше, передаточное отношение выражается как (зубья ведущей шестерни) : (зубья ведомой шестерни), так что пара шестерен, представленная выше, может быть выражена как 12:60 (или 12 к 60).

Передаточное число рассчитывается по формуле (зубья ведомой шестерни) / (зубья ведущей шестерни)

Поэтому передаточное число = Зубья ведомой шестерни / Зубья ведущей шестерни = 60/12 = 5

Глядя на пример, представленный выше. ..

Предельный перегрузочный момент второго вала может быть рассчитан по формуле:

Выходной момент = Входной момент х Передаточное число

Выходной момент = 1,5 Н-м х 5 = 7,5 Н-м

Свободная скорость второго вала может быть рассчитана по формуле:

Выходная скорость = Входная скорость / Передаточное число = 100 об/мин / 5 = 20 об/мин

Второй вал, таким образом, вращается со свободной скоростью 20 об/мин, при этом предельный перегрузочный момент равен 7,5 Н-м. При понижении скорости крутящий момент увеличивается.

Для второго примера расчеты могут быть произведены тем же способом.

Передаточное число = Зубья ведомой шестерни / Зубья ведущей шестерни = 12/60 = 0,2

Выходной момент = Входной момент х Передаточное число = 1,5 Н-м х 0,2 = 0,3 Н-м

Выходная скорость = Входная скорость / Передаточное число = 100 об/мин / 0,2 = 500 об/мин

Второй вал, таким образом, вращается со свободной скоростью 500 об/мин, при этом предельный перегрузочный момент равен 0,3 Н-м. При повышении скорости крутящий момент уменьшается.

 

8 Расчет крутящих моментов на валах

8.1 Расчет крутящего момента
на валу электродвигателя

Для
определения крутящего момента на валу
электродвигателя привода главного
движения используется номинальная
мощность и номинальная частота вращения:

где
– мощность электродвигателя, кВт:

–номинальная
частота вращения электродвигателя,
мин-1:

.

.

8.2 Расчет крутящего момента на валах
привода

Крутящий
момент на валах привода рассчитывается
по формуле:

где

– мощность электродвигателя, кВт:

–КПД
участка привода от электродвигателя
до соответствующего вала;

–расчетная
частота вращения соответствующего
вала, принимается по графику частот,
мин-1.

8.3 Расчет крутящего момента на первом
валу привода

Крутящий
момент на первом валу привода рассчитывается
по формуле:

где
– мощность электродвигателя, кВт:

–КПД
участка привода от электродвигателя
до 1-го вала;

–расчетная
частота вращения на 1-ом валу, принимаем
по графику частот, мин-1:
= 2850 мин-1.

КПД
участка привода до первого вала
рассчитывается по формуле:

где
– КПД зубчатой муфты;

–КПД
пары подшипников;

8.4 Расчет крутящего момента на втором
валу привода

Крутящий
момент на втором валу привода рассчитывается
по формуле:

где
– мощность электродвигателя, кВт:

–КПД
участка привода от электродвигателя
до 2-го вала;

–расчетная
частота вращения на 1-ом валу, принимаем
по графику частот, мин-1:
= 630 мин-1.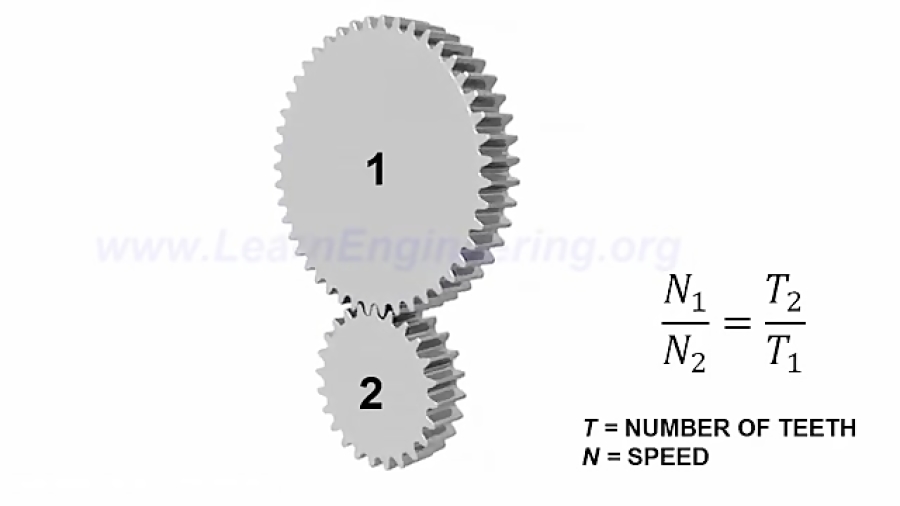

КПД
участка привода до второго вала
рассчитывается по формуле:

где
–
КПД зубчатой муфты;

–КПД
пары подшипников;

—
КПД зацепления зубчатых колес;
.

8.5 Расчет крутящего момента на третьем
валу привода

Крутящий
момент на третьем валу привода
рассчитывается по формуле:

где
– мощность электродвигателя, кВт:

–КПД
участка привода от электродвигателя
до 3-го вала;

–расчетная
частота вращения на 1-ом валу, принимаем
по графику частот, мин-1:
= 160 мин-1.

КПД
участка привода до третьего вала
рассчитывается по формуле:

где
–
КПД зубчатой муфты;

–КПД
пары подшипников;

—
КПД зацепления зубчатых колес;
.

8.6 Расчет крутящего момента на четвертом
валу привода

Крутящий
момент на четвертом валу привода
рассчитывается по формуле:

где
– мощность электродвигателя, кВт:

–КПД
участка привода от электродвигателя
до 4-го вала;

–расчетная
частота вращения на 4-ом валу, определяется
по формуле:

где
– минимальная частота вращения четвертого
вала, мин-1:

мин-1;

–максимальная
частота вращения четвертого вала, мин-1:

мин-1.

КПД
участка привода до четвертого вала
рассчитывается по формуле:

где
–
КПД зубчатой муфты;

–КПД
пары подшипников;

–КПД
зацепления зубчатых колес;
.

Крутящий
момент на шпинделе рассчитывается по
формуле:

где
– мощность электродвигателя, кВт:

–КПД
участка привода от электродвигателя
до шпинделя;

–расчетная
частота вращения шпинделя, определяется
по формуле:

где
– минимальная частота вращения четвертого
вала, мин-1:

мин-1;

–диапазон
регулирования частот вращения шпинделя:

КПД
участка привода до шпинделя рассчитывается
по формуле:

где
–
КПД зубчатой муфты;

–КПД
пары подшипников;

–КПД
зацепления зубчатых колес;
.

9 Проектный расчет передач

9.1 Расчет цилиндрической прямозубой
постоянной передачиz1–z2

9. 1.1
Исходные данные

1.
Расчетный крутящий момент на первом
валу привода, H·м:

Т1
=
13 Н·м;

2.
Число зубьев шестерни: z1
=
18;

3.
Число зубьев колеса: z2
=
83;

4.
Передаточное число передачи: u1
=
4,76.

9.1.2
Выбор материала и термической обработки
зубчатых
колес

В
качестве материала для зубчатых колес
передачи выбираем сталь 40Х, которая
отвечает необходимым техническим и
эксплуатационным требованиям. В качестве
термической обработки выбираем объемную
закалку, позволяющую получить твердость
зубьев 40..50HRCэ.

9.1.3
Проектный расчет постоянной прямозубой
зубчатой передачи
на контактную выносливость

Диаметр
начальной окружности шестерни
рассчитывается по формуле:

где

вспомогательный
коэффициент: для прямозубых передач

—
расчётный крутящий момент на первом
валу, Н·м: Т1=13
Н·м;

коэффициент
нагрузки для шестерни, равный 1,3. .1,5:
принимаем

—
передаточное число:

отношение
рабочей ширины венца передачи к начальному
диаметру шестерни:

допускаемое
контактное напряжение, МПа.

Допускаемое
контактное напряжение для прямозубых
передач рассчитывается по формуле:

где

базовый
предел контактной выносливости
поверхностей зубьев, соответствующий
базовому числу циклов перемены напряжений,
МПа;

МПа;

SH
– коэффициент безопасности: SH
= 1,1.

Коэффициент
отношения рабочей ширины венца передачи
к начальному диаметру шестерни может
приниматься в пределах

или
определяется
по формуле:

отношение
рабочей ширины венца передачи к модулю:
принимаем

число
зубьев шестерни: z1
= 18.

что
находится в допустимых пределах
.

Таким
образом, диаметр начальной окружности
шестерни равен:

Модуль
постоянной прямозубой передачи
определяется из условия расчета на
контактную выносливость зубьев по
рассчитанному значению диаметра
начальной окружности шестерни по
формуле:

где

диаметр
начальной окружности шестерни, мм:dw1
=
38,75 мм;

число
зубьев шестерни: z1
= 18.

Зубчатая передача: Расчет передаточного числа, крутящего момента и скорости

Зубчатая передача состоит из двух или более шестерен, соединенных последовательно. Он используется для увеличения или уменьшения скорости или крутящего момента выходного вала. Термин передаточное число используется для расчета скорости и крутящего момента выходной шестерни, когда крутящий момент прикладывается к входной шестерне.

Цилиндрическое зубчатое колесо в движении

Например, коробка передач — это тип зубчатой ​​передачи, который используется для увеличения крутящего момента двигателя и снижения скорости колес автомобиля. Увеличение крутящего момента зависит от того, на какой передаче вы едете на своем автомобиле. В этой статье мы обсудим, как рассчитать передаточное число, скорость и крутящий момент для различных зубчатых передач.

Чтобы понять передаточное отношение, мы предлагаем вам сначала прочитать эту статью о Терминологии передач (различные термины, используемые в передачах) и различных типах передач.

Закон зубчатой ​​передачи

Закон Закон зубчатой ​​передачи гласит, что отношение угловых скоростей между сопряженными шестернями всегда остается постоянным. Для достижения условия постоянной угловой скорости общие нормаль в точке контакта сопряженных зубьев шестерни всегда проходят через точку тангажа. Где Точка шага — это точка контакта между окружностями шага сопрягаемой шестерни.

Если угловая скорость сопряженной шестерни постоянна, мы можем заключить следующее соотношение:

Где ω1 и ω2: Угловая скорость в радианах/с для ведущей и ведомой шестерен соответственно.

n1 и n2 = скорость передачи в об/мин для ведущей и ведомой шестерен соответственно.

d1 и d2 = диаметр ведущей и ведомой шестерен соответственно.

T1 и T2 = Количество зубьев на ведущей и ведомой шестернях соответственно.

Передаточное число

Передаточное отношение — это отношение числа зубьев ведомой и ведущей шестерен. Он используется для расчета скорости и крутящего момента выходного вала, когда входной и выходной валы соединены зубчатой ​​передачей.

Входная шестерня, к которой прикладывается крутящий момент, известна как привод . В то время как выходная шестерня известна как ведомая шестерня . А шестерни, используемые между ведущей и ведомой шестернями, известны как промежуточные шестерни .

Передаточное отношение и скорость

Передача мощности через зубчатую передачу влияет на скорость вращения выходного вала.

Таким образом:

Скорость вторичного вала = Скорость входного вала / Передаточное число

Передаточное отношение

Как показано выше, если число шестерен на выходном валу больше, чем шестерен на входном валу. Эта компоновка также известна как редуктор . При таком расположении выходной вал будет иметь более низкую скорость по сравнению с входным валом.

Цилиндрическое зубчатое колесо для увеличения скорости

Принимая во внимание, что когда мы реверсируем расположение. Другими словами, если количество шестерен на вторичном валу меньше, чем шестерен на входном валу. Скорость выходного вала будет иметь большую скорость по сравнению с входным валом.

Передаточное число и крутящий момент

Согласно закону передаточных чисел. В зубчатой ​​передаче отношение выходного крутящего момента к входному крутящему моменту также постоянно и равно передаточному числу. Следовательно, если входной крутящий момент известен. Выходной крутящий момент можно рассчитать, умножив входной крутящий момент на передаточное число.

Типы зубчатых передач и их расчет

Зубчатая передача состоит из ряда шестерен для передачи мощности от одного вала к другому. Например, мощность от двигателя передается на колеса через коробку передач. Вот четыре различных типа зубчатой ​​передачи.

  1. Простая зубчатая передача
  2. Составная зубчатая передача
  3. Реверсивная зубчатая передача
  4. Планетарная зубчатая передача

1) Расчет передаточного числа для простой зубчатой ​​передачи

Простая зубчатая передача может быть двухступенчатой ​​или многоступенчатой.

1.1) Двухступенчатая передача

Двухступенчатая передача — это тип простой зубчатой ​​передачи. Он состоит из двух соединенных шестерен. Например, как показано ниже в двухступенчатом поезде. Gear-1 является ведущей, а Gear-2 — ведомой. Когда ведущая шестерня вращается по часовой стрелке, ведомая шестерня будет вращаться против часовой стрелки.

Вопрос:  Рассчитайте скорость и крутящий момент выходного вала для простой зубчатой ​​передачи. Где количество зубьев на ведущей и ведомой шестернях 40 и 20 соответственно. Шестерня привода вращается со скоростью 100 об/мин и крутящим моментом 10 Нм.

Количество зубьев ведущей шестерни (T1) = 40

Количество зубьев ведомой шестерни (T2) = 20

Скорость ведущей шестерни (n1) = 100 об/мин

Двухступенчатая передача

Расчет передаточного числа

GR = T2 / T1 = 20/40 = 0. 5

Расчет скорости выходного вала

Скорость выходного вала/ Шестерня = n1/GR = 100/0,5 = 200 об/мин

Расчет крутящего момента выходного вала/шестерни

Крутящий момент, создаваемый ведомой шестерней = GR × Крутящий момент, создаваемый приводом

= 0,5 × 10 = 5 Н·м зубчатые передачи состоят из более чем двух шестерен, передача движения с одного вала на другой. Результирующее передаточное число может быть рассчитано путем умножения отдельных передаточных чисел.

Вопрос:  Рассчитайте передаточное число для многоступенчатых поездов. Где количество зубьев на ведущей, промежуточной и ведомой шестернях составляет 40, 20 и 10 соответственно.

Многоступенчатая передача

Заданное количество зубьев

T1 = 40, T2 = 20, T2 = 10

Расчет передаточного числа (GR) для многоступенчатой ​​передачи 1: Расчет передаточного числа между Gear-1 и Gear-2 (водитель и натяжитель).

GR(1-2) = 20/40 = 0,5

Шаг 2: Рассчитайте GR между шестерней-2 и шестерней-3 (промежуточная и ведомая шестерни).

GR(2-3) = 10/20 = 0,5

Шаг 3: Путем умножения передаточного числа между 1 к 2 и 2 к 3. Мы получим результирующий GR между ведущей и ведомой шестернями.

Результирующая многоступенчатая передача GR = 0,5 × 0,5 = 0,25

Из вышеприведенного расчетного передаточного числа мы можем рассчитать скорость и крутящий момент на выходной передаче.

2) Расчет передаточного числа для составной зубчатой ​​передачи

Составные шестерни состоят из более чем одной шестерни на одной оси. Поэтому шестерни на одном валу вращаются с одинаковой скоростью и крутящим моментом.

Вопрос:  Рассчитайте передаточное число составной зубчатой ​​передачи. Где количество зубьев на ведущей и ведомой шестернях 40 и 10 соответственно с одной составной шестерней. Составная шестерня имеет одну шестерню, соединенную с ведущей шестерней с 30 зубьями, и другую шестерню, соединенную с ведомой шестерней с 20 зубьями.

Составная зубчатая передача

Заданное число зубьев

T1 = 40, T2 = 30, T3 = 20, T4 = 10

Расчет передаточного числа для составной шестерни

Шестерня-2 и Шестерня -3  находятся на одном валу.

Шаг-1: Рассчитать передаточное отношение между Шестерня-1 и Шестерня-2

GR(1-2) = 30/40 = 0,75 4.

ГР(3-4) = 10/20 = 0,5

Шаг 3: Умножить GR(1-2) и GR(3-4)

Полученная составная шестерня GR = 0,375

3) Перевернутая зубчатая передача.

Реверсивная зубчатая передача

Реверсивная зубчатая передача представляет собой тип составной зубчатой ​​передачи, в которой входной и выходной валы находятся на одной оси. В приведенном выше примере шестерня-1 и шестерня-3 находятся на одной оси.

Используются для достижения высокого передаточного числа в ограниченном пространстве. Передаточное число реверсивной зубчатой ​​передачи рассчитывается аналогично составной зубчатой ​​передаче.

Подводя итог, можно сказать, что передаточное число используется для расчета результирующей скорости передачи и крутящего момента. Величина передаточного отношения зависит от количества зубьев на ведущей, промежуточной и ведомой шестернях. Мы предлагаем вам сначала прочитать эту статью о редукторах.

Есть вопросы?  

Будем рады помочь.

Если вы думаете, что мы что-то пропустили? Вы можете дополнить эту статью, отправив сообщение в поле для комментариев. Мы постараемся добавить его в этот пост.

После понимания этой статьи мы предлагаем вам сдать этот экзамен, чтобы подтвердить свои знания и понимание.

Знание крутящего момента зубчатой ​​передачи

  • ВЕРШИНА

    • >

  • Знание передач

    • >

  • Первый шаг конструкции механизма с использованием шестерен

    • >

  • Знать о крутящем моменте зубчатой ​​передачи

1. Функции редуктора

Вот список функций зубчатых передач для конструкций механизмов. (Таблица 3-1)

Таблица 3-1 Функции редуктора

Характерные функции шестерен Объяснение
Изменить направление вращения вала (уже объяснил)
Преобразование вращательного движения в линейное движение (уже объяснил)
Изменение направления вращения (по часовой стрелке/против часовой стрелки) (уже объяснил)
Изменение количества оборотов (ускорение вверх/вниз) (уже объяснил)
Изменение силы вращения (увеличение/уменьшение крутящего момента) См. эту главу

Вы можете увеличить или уменьшить крутящий момент шестерни (крутящую силу), изменив число оборотов.

2. Определение крутящего момента (крутящего момента)

Крутящий момент представляет собой вращающую силу, когда нагрузка F (Н) приложена на расстоянии L (мм) от центра вращения. Крутящий момент Т выражается следующей формулой в Н·мм (Ньютон-миллиметр). (Рисунок 3-1)


Рисунок 3-1 Момент затяжки

Крутящий момент T становится больше по мере того, как L (расстояние от центра вращения) становится больше, даже если нагрузка F мала. С другой стороны, крутящий момент T становится больше по мере увеличения нагрузки F, даже если L (расстояние от центра вращения) короткое.
Другими словами, крутящий момент T — это коэффициент, определяемый L (расстояние от центра вращения) и нагрузкой F.

3. Как определить передачу крутящего момента (без учета КПД машины)

Крутящий момент передачи изменяется при увеличении или уменьшении скорости. Как правило, при снижении скорости небольшой крутящий момент на входной стороне передается как больший крутящий момент на выходной стороне. Расчет крутящего момента зависит от количества зубьев. Позвольте мне объяснить с помощью диаграммы с использованием диаметров делительной окружности.
Крутящий момент рассчитывается следующим образом:

  1. Получите нагрузку F точки зацепления (на радиусе делительной окружности шестерни A) от входного крутящего момента.
  2. Получите крутящий момент выходной стороны от нагрузки F точки зацепления зубьев (радиус делительной окружности шестерни B).


Состояние
Номинальный крутящий момент двигателя: TA=600 Н·мм (0,6 Н·м)
Диаметр делительной окружности шестерни А φ20
Диаметр делительной окружности шестерни В φ40


Расчет передачи крутящего момента
Нагрузка в точке зацепления шестерни A: F=TA/LA=60(Н)
Крутящий момент на выходной стороне: TB=F×LB=60(Н)×20(мм)=1200(Н·мм )

Рисунок 3-2 Схема расчета передачи крутящего момента шестерни

Как видно из рисунка 3-2, при уменьшении скорости выходного вала относительно входного вала на 1/2 выходной крутящий момент увеличивается в 2 раза.

4. Рассмотрение эффективности машины

Как показано в предыдущей главе, количество оборотов шестерни можно рассчитать по количеству зубьев.
Однако вы не можете рассчитать крутящий момент передачи просто так, как показано выше, по следующим причинам:

  • При зацеплении зубьев выделяется тепло, и энергия теряется.
  • Звук молотка издается зацеплением зубов, и энергия теряется.

Следовательно, крутящий момент (крутящая сила) уменьшается на столько, на сколько теряется энергия, как указано выше.
Отношение входных и выходных усилий зубчатых колес называется «КПД машины», и его приблизительное значение известно в зависимости от типа зубчатого колеса. (Таблица 3-2)

Таблица 3-2 КПД редуктора по типу

Связь двух валов Название шестерни КПД машины η (%)
параллельный вал цилиндрическое прямозубое колесо98,0 — 99,5
*
КПД косозубого колеса меньше, чем прямозубого, так как зубья наклонены и усилие создается в направлении тяги.
косозубая шестерня
двойная косозубая шестерня
внутренняя шестерня
стойка
винтовая стойка
пересекающийся вал прямая коническая шестерня 98,0 — 99,0
спирально-коническая шестерня
перекошенный вал червячный редуктор 30,0 — 90,0
винтовая передача 70,0 — 95,0

Примечание. Показанный выше КПД представляет собой КПД зубчатых передач без учета потерь в подшипниках или перемешивания смазки.
Эффективность шестерни, показанная выше, является значением, когда шестерни установлены правильно. При неправильной установке, например отклонении в точке пересечения конических шестерен, эффективность снизится.


«Никогда не забывайте об эффективности машины при расчете крутящего момента!»

5.

Расчет крутящего момента трансмиссии (включая КПД машины)

Теперь давайте посмотрим на формулу расчета крутящего момента, включая КПД машины η. (Рисунок 3-3)

Когда входной крутящий момент шестерни А равен TA, а КПД машины равен η, крутящий момент TB, который передается на шестерню B, увеличивается по мере увеличения эффективности η.

ТБ=η（ZB/ZA）× ТА

Когда входной крутящий момент шестерни B равен TB, крутящий момент TA, который передается на шестерню A, уменьшается по мере падения эффективности η.

TA=η（ZA/ZB）× ТБ

Рисунок 3-3 Формула расчета крутящего момента трансмиссии

Упражнение для передачи крутящего момента (1)

Рассчитайте крутящий момент, передаваемый на ведомую шестерню (B). Предположим, что тип шестерни — прямозубая.
Символ на Рисунке 3-4 представляет ведущую шестерню.

[Условие]
Количество зубьев: ZA=20, ZB=40
Крутящий момент ведущей шестерни A: TA=600 (Н·мм)
КПД машины η: Установите на 0,99, так как используются прямозубые шестерни.

[Ответ]
Крутящий момент, передаваемый на шестерню B
TB=η(ZB/ZA)×TA
= 0,99(40/20)×600=1188(Н·мм)

Рисунок 3-4 Упражнение для передачи крутящего момента (1)

Упражнение для передачи крутящего момента (2)

Рассчитайте крутящий момент, передаваемый на червячное колесо B. (Рисунок 3-5)

[Условие]
Количество зубьев: ZA=1, ZB=30
Крутящий момент червяка A: TA=600 (Н·мм)
КПД машины η: Установите на 0,3, поскольку используются червячные передачи.

[Ответ]
Крутящий момент, передаваемый на червячное колесо B
TB=η(ZB/ZA)×TA=0,3(30/1)×600
= 5400(Н·мм)

Рисунок 3-5 Упражнение для передачи крутящего момента (2)

Упражнение для передачи крутящего момента (3)

Рассчитайте крутящий момент, передаваемый на ведомую шестерню (С). Предположим, что тип шестерни — косозубая шестерня.
Символ на рис. 3-6 представляет ведущую шестерню.

[Условие]
Количество зубьев: ZA=20, ZB=30, ZC=20
Крутящий момент ведущей шестерни A: TA=500 (Н·мм)
КПД машины η: Установите на 0,98, так как используются косозубые шестерни.

[Ответ]
Крутящий момент, передаваемый на шестерню B
TB=η(ZB/ZA)×TA
=0,98(30/20)×500=735(Н·мм)
Крутящий момент, передаваемый на шестерню C
TC=η(ZB/ ZC)×NB
=0,98(20/30)×735=480,2(Н·мм)

Рисунок 3-6 Упражнение для передачи крутящего момента (3)


«Как и количество оборотов, количество зубьев первой и последней шестерен определяет крутящий момент одноступенчатой ​​шестерни, но крутящий момент уменьшается, поскольку эффективность машины зависит от количества промежуточных шестерен!»

Упражнение для передачи крутящего момента (4)

Рассчитайте крутящий момент, передаваемый на ведомую шестерню (D). Предположим, что тип шестерни — косозубая шестерня.
Символ на Рисунке 3-7 представляет ведущую шестерню.

[Условие]
Количество зубьев: ZA=20, ZB=40, ZC=20, ZD=30
Крутящий момент ведущей шестерни A: TA=400 (Н·мм)
КПД машины η: установлено на 0,98, так как используются косозубые шестерни. .

[Ответ]
Крутящий момент, передаваемый на шестерню B
TB=η(ZB/ZA)×TA
=0,98(40/20)×400=784(Н·мм)
Крутящий момент, передаваемый на шестерню C
TC=TB=784( Н·мм)… как на одном валу
Крутящий момент, передаваемый на шестерню D
TD=η(ZD/ZC)×TC
=0,98(30/20)×784=1152,5(Н·мм)

Рисунок 3-7 Упражнение для передачи крутящего момента (4)

Приступая к проектированию механизма с использованием зубчатых передач, важно помнить об эффективности машины. Механизм, спроектированный без учета КПД машины, может не соответствовать спецификациям из-за нехватки крутящего момента.
Мы обсуждали, что эффективность машины влияет на крутящий момент передачи в зависимости от типа шестерни и количества зацеплений.
Далее мы объясним параметры, которые определяют форму зубчатых колес при проектировании зубчатых колес.
(Продолжение следует…)

*Иллюстрация: КАОСУН

ОТКАЗ ОТ ОТВЕТСТВЕННОСТИ

Цель написания этой статьи состояла в том, чтобы обучить читателей элементарному уровню зубчатой ​​техники.

Posted inПопулярное