3 = /3 = /4,.-.
Пример. Определить сечения голых алюминиевых проводов четырехпроводной воздушной линии трехфазного тока напряжением 380/220 в, длиной 100 м, по которым передается мощность 12 кет для питания электрического освещения дома (рис. 5-23) . Допускаемая потеря напряжения в линии 2%. Нагрузка на расчетной схеме указана стрелкой, длина в метрах указана подчеркнутой цифрой.
Определяем момент нагрузки: М — 12 100 = 120о квт-м.
формулой,
Определяем сечение фазных проводов, пользуясь приведенной в начале параграфа, и табл. 5-4:
Л1
СД№/„
1 200 46-2
= 13 мм2.
Берем ближайшее большее стандартное сечение 16 л.и2 для фазных проводов и 16 лиг2 для нулевого провода как наименьшее сечение, допускаемое ПУЭ по условиям механической прочности проводов воздушных линий.
Пример. Определить сечение медного провода двухпроводной линии постоянного тока. Напряжение сети ПО в. Линия выполнена
SO302Р_
it г к
юо |
Рис. |
Рис. 5-24.
проводами одинакового сечения по всей длине. Нагрузки (нет) указаны стрелками на рис. 5-24, длины (м) — подчеркнутыми цифрами. Допускаемая потеря напряжения в линии 2,5%. (н* 1ролив/ _
Определяем момент нагрузки
М = 6 • 50 4- 1 -80 — 4 • 100 — 780 нет ■ м.
Определяем сечение провода
А1
S _ CAT»»/,,
780
3 2 • 2 5
= 97,5
мм-.
Берем ближайшее стандартное сечение провода 95 .им2.
Пример. Определить сечение провода марки АПР-500 двухпровод-
ной линии переменного тока. Напряжение сети 220 в. Допускаемая потеря напряжения в линии 1%. Сечение проводов одинаково по всей длине. Нагрузки на рис. 5-25 приведены в ваттах, длины — в метрах.
1010№№1010]£1Q
Г Г г т”гтттп
I5O 10 I5O ISO ISO ISO ISO 15O
Hl
Рис. 5-25,
100-8
2
1(150*8)
Рис. 5-2fi.
Пользуясь указаниями, приведенными в начале параграфа, заменяем расчетную схему (рис.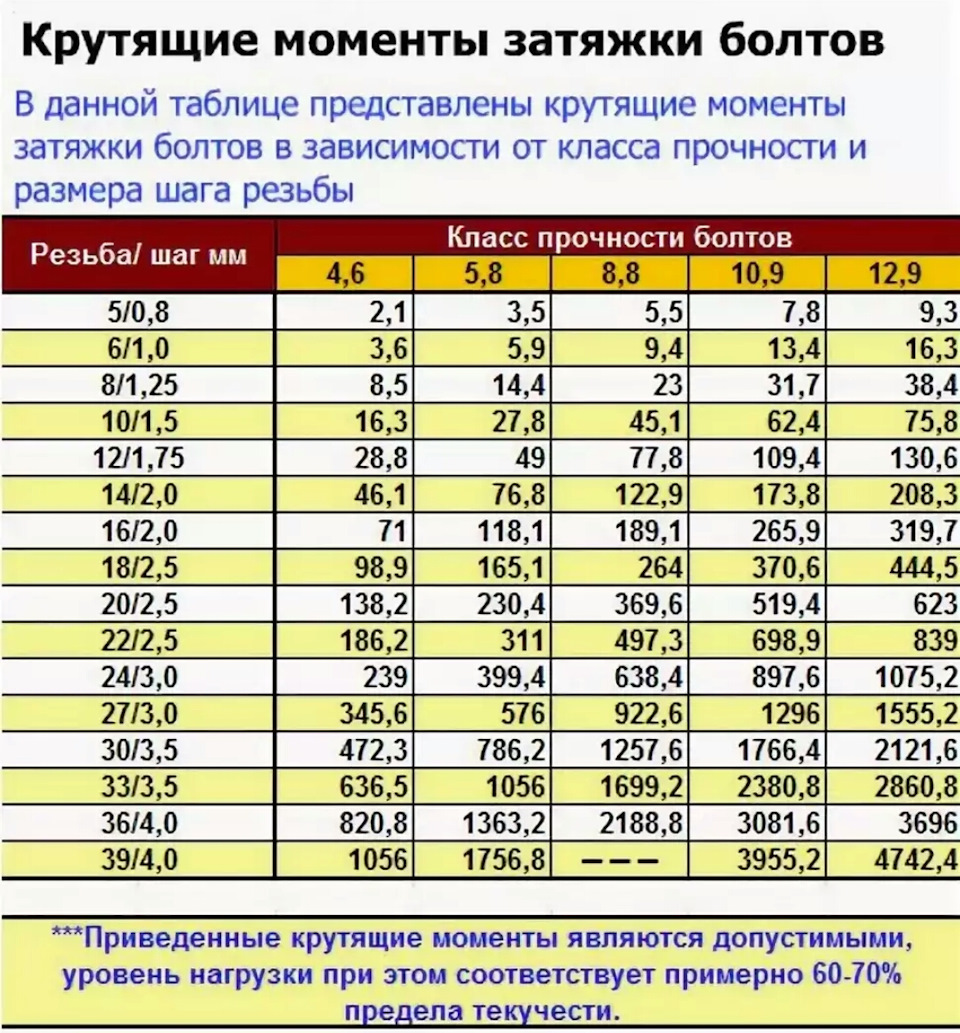
нет •.w—
= 48
Определяем сечение
Л1 _ 48
6,2 мм2,
S “ САТ%„ — 7,Г“1
Берем ближайшее стандартное сечение провода 6 мм3.
Б-21. ОПРЕДЕЛЕНИЕ ПОТЕРИ НАПРЯЖЕНИЯ В ЛИНИЯХ С ПРОВОДАМИ ОДИНАКОВОГО СЕЧЕНИЯ ПО ВСЕЙ ДЛИНЕ
Определение потери напряжения в линиях при проводах и кабелях с медными и алюминиевыми жилами производится по формуле
М. Cs ’
Д£% =
где ДС% — потеря напряжения, % номинального напряжения сети; Л4 — момент нагрузки, квт-м;
С — коэффициенты, приведенные в табл. 5-4;
s — сечение жилы провода, мм2.
Определение потери напряжения в трехфазных линиях со сталь-
ными проводами производится приближенно по формуле
где % — коэффициенты, приведенные в табл. 5-4.
М — мо,мент нагрузки, квт-м.
Пример. Определить потерю напряжения в однофазной групповой линии пере.менного тока длиной 50 м. Напряжение сети 220 в. Линия выполнена проводом марки ПР-500 сечением 4 мм2. Нагрузки на рис. 5-22 указаны в ваттах, длины — в метрах.в|||
Нагрузки на рис. 5-22 указаны в ваттах, длины — в метрах.в|||
ГЬ££ в $
i i ? 5 {
зоо зоо 3UI 300 300
Рис. 5-27.
Ж+Т
17,5 кет.
Рис. 5-28.
Заменяем расчетную схему на рис. 5-27 схемой, изображенной на рис. 5-28. Определяем момент нагрузки и длину:
Р = 300 — 5 = 1 500 вт = 1,5 кетL — 26 += 38 м- М = 1,5 • 38 = 57 кет ■ м.
Потеря напряжения будет равна:
~ Cs= 12,8-411 “/в-
При проводах с алюминиевыми жилами того же сечения потеря напряжения равнялась бы;
1,85%
fjsQ В. М. Чумаков
Пример. Определить потерю напряжения в проводах трехфазной воздушной линии длиной 50 м при напряжении 380/220 в и передаче по ним мощности 6 кет. Линия выполнена
Sqпроводами из отожженной Стальной катанки
О-—диаметром 5 мм (рис. 5-29) .
{бОпределяем момент нагрузки
Рис 5.29/И = 6- 50 = 300 кет — м.
Находим потерю напряжения по формуле
Л!
AA/o/o=-—g-, причем значение Q находим по табл.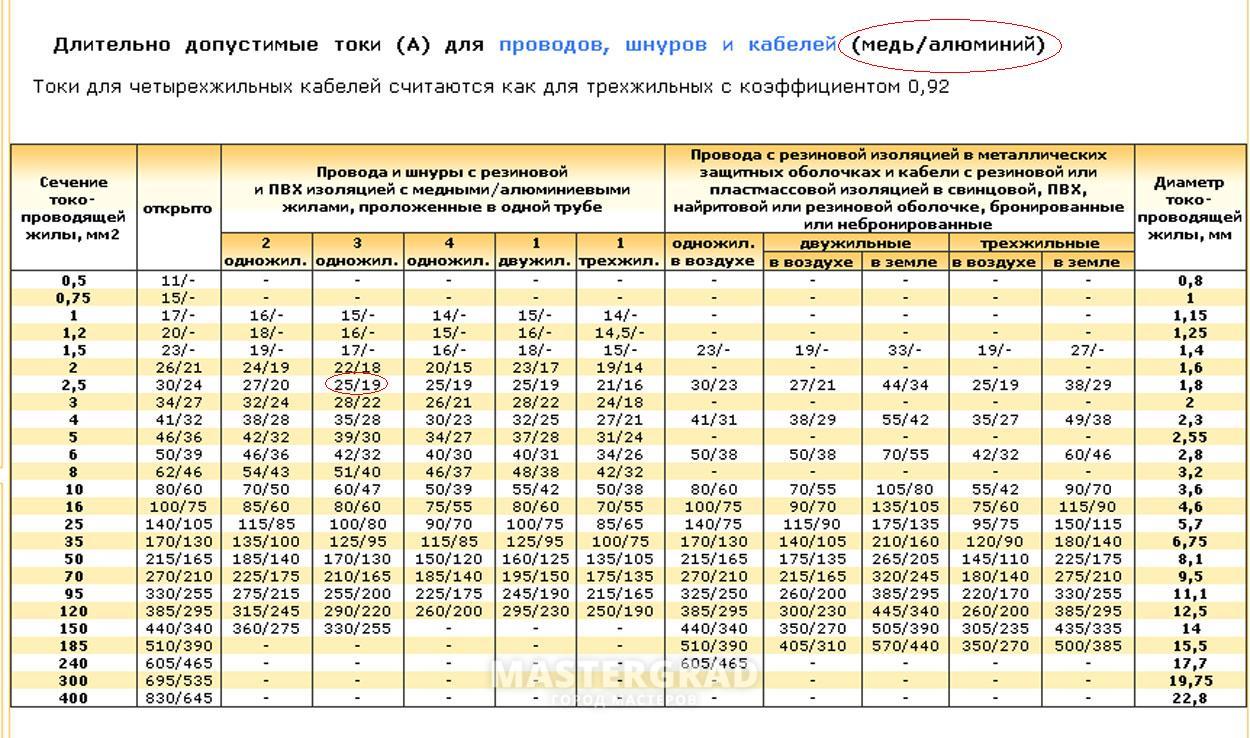 ф/ф cos tp.
ф/ф cos tp.
2. Соотношения между током и напряжением при трехфазном токе
Соединение звездой: /л = 1$; 7/;| = 1,73ф.
Соединение треугольником: /л = 1,73/ф; U:t = Сф.
В приведенных формулах:
/л и Пл — линейные ток и напряжение;
/ф и (7ф — фазные ток и напряжение;
Р — сопротивление проводов (при переменном токе — активное) .
3. Величина тока при различных мощностях и напряжениях | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
Содержание
Что такое «момент нагрузки» кабеля
При проектировании электрических сетей приходится рассчитывать потери напряжения.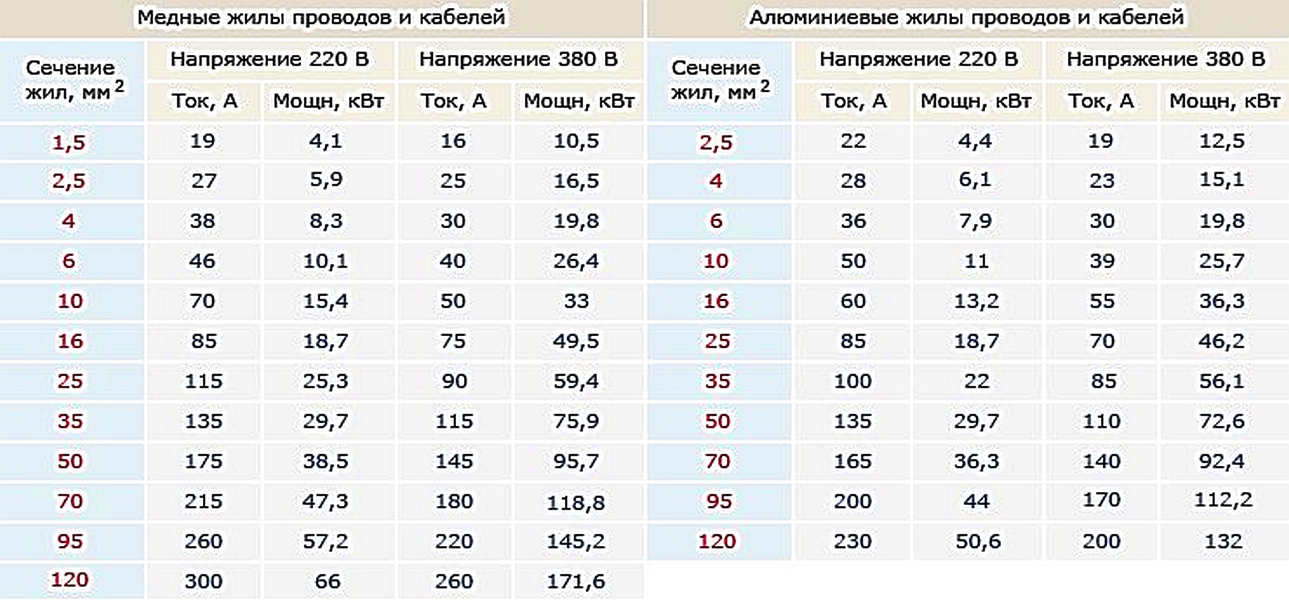
Требования по размещению данных о моменте нагрузки на групповых линий указаны в ГОСТ 21.608-2014 Система проектной документации для строительства (СПДС). Правила выполнения рабочей документации внутреннего электрического освещения. Ссылка на гост.
Существуют разные способы расчета, но все они, в принципе, основаны на одних и тех же формулах, поэтому и результаты должны быть одинаковые. Так ли это? Сейчас мы проверим.
Многие считают потери напряжения через моменты нагрузок. Давайте с вами разберем расчет потери напряжения через «Момент нагрузки»
Что такое момент нагрузки?
М=P*L, где
М – момент нагрузки, кВт*м;
Р – мощность, кВт;
L – длина участка, м.
Чтобы рассчитать потери напряжения через момент нагрузки нам необходимо знать расчетную мощность потребителя, длину кабельной линии и дополнительные данные.
По формуле dU=P*L/(C*q).
Где q — сечение проводника.
С — коэффициент, зависящий от материала проводника и напряжения сети.
Для меди С=77.
Для алюминия — 44.
Таблицу расчета момента нагрузки с настроенными формулами в формате Excel, можно скачать тут.
Формули и расчеты
Расчет освещения строительной площадки
Как считать электрическую мощность?
Виды аварийного освещения
Схема аварийного освещения
Однолинейная схема электроснабжения
Проверка аварийного освещения
Когда включается эвакуационное освещение?
Эвакуационное освещение требования:
Какой кабель нужен для розеток?
Кабель для электроплиты
Установка УЗО на уличные розетки, ставить или нет?
Какая высота установки вызывных панелей для МГН ?
Высота ручного пожарного извещателя
Кабель ввгнг-ls или ппгнг-hf, какой выбрать
Что такое «момент нагрузки»
Проектирование электроснабжения
Проектирование СКС
Проектирование диспетчеризации
Проектирование АПС
Пожарная безопасность стадионов
Среди общественных зданий, сооружений спортивные, физкультурно-оздоровительные объекты выделяются повышенной…
подробнее
Монтаж слаботочных систем.
 ч.2
ч.2
Слаботочные системы — это локальные сети, работающие на безопасном уровне для жизни человека. Благодаря…
подробнее
Освещение в квартире
Правильная организация освещения в квартире служит основным фактором создания теплой атмосферы уюта и комфорта, в которую…
подробнее
Беспроводные локальные сети
Беспроводная локальная сеть ( WLAN ) — локальная сеть, в которой соединения между сетевыми устройствами…
подробнее
Пожарная безопасность гостиниц
При планировании поездки в новые города, знаменитые природными, историко-архитектурными достопримечательностями, путешественники…
подробнее
Теплый пол электрический в ванной
Ванна – это именно то место, где больше всего хочется ощущать тепло не только телом, да еще и мокрым,…
подробнее
Кручение валов
Напряжение сдвига в валу
Когда вал подвергается крутящему моменту или скручиванию, в валу возникает напряжение сдвига.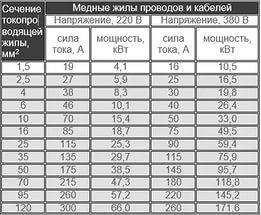 Касательное напряжение меняется от нуля на оси до максимума на внешней поверхности вала.
Касательное напряжение меняется от нуля на оси до максимума на внешней поверхности вала.
Касательное напряжение в сплошном круглом валу в заданном положении может быть выражено как:
τ = T r / J (1)
где 9 0013
τ = напряжение сдвига (Па, фунт f /фут 2 (фунт/фут))
T = крутящий момент (Нм, фунт f футов)
r = расстояние от центр к напряженной поверхности в заданном положении (м, фут)
J = полярный момент инерции площади (м 4 , фут 4 )
Примечание
9005 1
 . (фунт f /фут 2 ) = 1/144 psi (фунт f /в 2 )
. (фунт f /фут 2 ) = 1/144 psi (фунт f /в 2 ) « Полярный момент инерции площади » также называется « Полярный момент инерции «, « Второй момент площади «, « Площадь момента инерции «, «9005 9 Полярный момент Area » или « Second Area Moment «.
Полярный момент инерции в зависимости от момента инерции площади
- «Полярный момент инерции» — мера способности балки сопротивляться скручиванию, необходимая для расчета скручивания балки, подвергаемой крутящему моменту
- «Момент инерции площади» — свойство формы, которое используется для прогнозирования прогиба, изгиба и напряжения в балках
Круглый вал и максимальный момент или крутящий момент
Максимальный момент в круглом валу может быть выражен как:
T макс. = τ макс. J / R (2)
9 0012, где
T max = максимальный крутящий момент (Нм, фунт f ft)
τ макс.
6 )
R = радиус вала (м, фут)
Комбинация (2) и (3) для цельного вала
T max = (π / 16) τ max D 3 (2b)
Объединение (2) и (3b) для полый вал
T max = (π / 16) τ max (D 4 — d 9002 5 4 ) / D (2c)
Круглый вал и полярный Момент инерции
Полярный момент инерции круглого сплошного вала можно выразить как
J = π R 4 / 2
= π (D / 2 ) 4 / 2
= π D 4 / 32 (3)
где
D = наружный диаметр )
Полярный момент инерции круглого полого вала может быть выражен как
(3б)
d = внутренний диаметр вала (м, футы)
Диаметр сплошного вала
Диаметр сплошного вала можно рассчитать по формуле
D = 1,72 ( T max / τ 90 023 max ) 1/3 (4)
Прогиб вала при кручении
Угловой прогиб вала при кручении может быть выражен как
α = L T / (J G) (5)
где
α = угловое отклонение вала (радианы)
L = длина вала (м, футы) G = модуль жесткости при сдвиге или модуль жесткости (Па, psf)
Угловое отклонение сплошного вала при кручении можно выразить как (5a)
Угловое отклонение кручения полый вал может быть выражен как
α = 32 L T / (G π (D 4 — d 4 )) (5b)
Угол в градусах можно получить, умножив угол θ в радианах на 180/№.
S вал ( π заменен)
α градусы ≈ 584 L T / (G D 4 ) (6a)
Полый вал ( π заменен)
α градусов ≈ 584 L T / (G (D 4 — d 90 025 4 ) (6b)
Моменты сопротивления кручению от валов различного поперечного сечения
| Площадь поперечного сечения вала | Максимальный крутящий момент Сопротивляющий момент — T макс. — (Нм, фунт f футов) | Номенклатура | |
|---|---|---|---|
| Цельный цилиндрический вал | (π / 16) τ макс. (2 r) 3 = (π / 16) τ max D 3 | ||
| Полый цилиндрический вал | (π / 16) τ max ((2 R) 4 — (2 r) 4 ) / (2 R) = (π / 16) 900 12 τ макс. | ||
| Эллиптический вал | (π / 16) 90 012 τ макс. б 2 ч | h = «высота» вала b = «ширина» вала h > b | |
| Прямоугольный вал | (2 / 9) τ макс. 900 24 b 2 h | h > b | |
| Квадратный вал | (2 / 9) τ макс H 3 | ||
| 9 0404 | Треугольный вал | (1 / 20) τ max b 3 | b = длина стороны треугольника |
| Шестигранный вал | 0,123 τ макс. D 3 0,189 τ макс б 3 | ||
Пример.
 Напряжение сдвига и угловой изгиб в сплошном цилиндре
Напряжение сдвига и угловой изгиб в сплошном цилиндре
Момент 1000 Нм действует на вал сплошного цилиндра диаметром 50 мм 90 013 (0,05 м) и длина 1 м . Вал изготовлен из стали с модулем жесткости 79 ГПа (79 10 9 Па) .
Максимальное напряжение сдвига можно рассчитать как
τ max = T r / J
= T (D / 2) / ( π D 4 / 32)
= (1000 Нм) ((0,05 м) / 2) / ( π (0,05 м) 4 / 32)
= 40764331 Па
= 40,8 МПа
9 0006 Угловое отклонение вала можно рассчитать как
θ = L T / (J G)
= L T / ( ( π D 4 / 32) G)
= (1 м) (1000 Нм) / ( ( π (0,05 м) 4 / 3 2) (79 10 9 Па))
= 0,021 (радианы)
= 1,2 o
Пример.
 Напряжение сдвига и угловой изгиб в полом цилиндре
Напряжение сдвига и угловой изгиб в полом цилиндре
9 0006 Момент 1000 Нм действует на полый цилиндрический вал с наружным диаметром 50 мм (0,05 м) , внутренний диаметр 30 мм (0,03 м) и длина 1 м . Вал изготовлен из стали с модулем жесткости 79 ГПа (79 10 9 Па) .
Максимальное напряжение сдвига можно рассчитать как π (Д 4 — д 4 ) / 32)
= (1000 Нм) ((0,05 м) / 2) / ( π ((0,05 м) 4 — (0,03 м) 4 ) / 32)
= 46,8 МПа 900 07
Угловое отклонение вала можно рассчитать как
θ = L T / (J G)
= L T / (( π D 4 / 32) G)
= (1 м) (1000 Нм) / ( ( π ((0,05 м) 4 — (0,03 м) 4 ) / 32) (79 10 9 Па))
= 0,023 радиан)
= 1,4 o
Пример — Диаметр вала, необходимый для передачи мощности
Электродвигатель 15 кВт должен использоваться для передачи мощности через присоединенный сплошной вал. Двигатель и вал вращаются с 2000 об/мин . Максимально допустимое напряжение сдвига — τ max — в валу 100 МПа .
Двигатель и вал вращаются с 2000 об/мин . Максимально допустимое напряжение сдвига — τ max — в валу 100 МПа .
Связь между мощностью и крутящим моментом может быть выражена
P = 0,105 n об/мин T (7)
где
P = мощность (Вт)
n об/мин = скорость вала (об/мин)
Перекомпонованы и со значениями — можно рассчитать крутящий момент
T = (15 10 3 Вт) / (0,105 (2000 об/мин))
= 71 Нм
Минимальный диаметр вала можно рассчитать по формуле 4
D = 1,72 ((71 Нм) / (100 10 6 Па)) 1/3
= 0,0153 м 9 0007
= 15,3 мм
Как рассчитать инерцию нагрузки
Помимо крутящего момента или скорости, при выборе двигателя следует учитывать еще один фактор.
Вы когда-нибудь задумывались, почему колеса и шины гоночного велосипеда отличаются от горного? Это связано с тем, что в гоночных велосипедах для повышения производительности используются более легкие и тонкие колеса. Более легкие и тонкие колеса уменьшают момент инерции колес; облегчая торговлю вразнос. В гонках, где счет идет на миллисекунды, немного значит очень много.
| Что такое «Инерция»? |
Инерция происходит от латинского слова iners , что означает бездействие или вялость. Инерция определяется как сопротивление любого физического объекта любому изменению его скорости. Чем больше инерция, тем более устойчивым он будет к ускорению или замедлению.
| Что такое «инерция нагрузки»? |
Инерция нагрузки или момент инерции — это сопротивление любого физического объекта любому изменению его скорости с точки зрения оси вращения. Для вращающейся нагрузки это произведение ее массы на квадрат перпендикулярного расстояния массы от оси. Инерция нагрузки обычно обозначается буквой «J».
Для вращающейся нагрузки это произведение ее массы на квадрат перпендикулярного расстояния массы от оси. Инерция нагрузки обычно обозначается буквой «J».
| Что такое «Допустимая инерция нагрузки» и «Коэффициент инерции»? |
Двигатели не могут управлять бесконечной инерцией нагрузки. Производители часто предлагают допустимую инерцию нагрузки или значение коэффициента инерции для двигателей, чтобы помочь с размером двигателя. Допустимая инерция нагрузки Значения являются ориентировочными, обычно приводимыми для двигателей переменного тока и бесщеточных двигателей (примеры приведены в конце поста). Коэффициент инерции с обычно дается для шаговых или серводвигателей и рассчитывается путем деления общей величины инерции нагрузки (или отраженной инерции нагрузки, если используется редуктор) на инерцию ротора двигателя. Если эти значения превышены, двигатель может пропускать шаги, глохнуть или вибрировать. Двигатели с замкнутым контуром могут работать с большим коэффициентом инерции, чем двигатели с незамкнутым контуром.
Двигатели с замкнутым контуром могут работать с большим коэффициентом инерции, чем двигатели с незамкнутым контуром.
Пример: рекомендуемые допустимые коэффициенты инерции
| Тип двигателя | Размер корпуса (мм) | Типоразмер (NEMA) | Коэффициент инерции |
| Шаговые двигатели с разомкнутым контуром | 20, 28, 35 | 8, 11, 14 | 5:1 или меньше |
| Шаговые двигатели с разомкнутым контуром | 42, 50, 56,4, 60, 85 | 17, 20, 23, 24, 34 | 10:1 или менее |
| Шаговые двигатели с обратной связью | — | — | 30:1 или менее |
| Серводвигатели (автоматическая настройка) | — | — | 50:1 или менее |
| Серводвигатели (ручная настройка) | — | — | 100:1 или менее |
СОВЕТ : Если вам необходимо превысить коэффициент инерции нагрузки. .. .. |
| Помните, что это безопасная рекомендация, и эти значения могут быть превышены при правильной настройке. Я помню, как разговаривал с кем-то, кто строил игровые автоматы для казино (старые с рычагом). Его команда использовала шаговый двигатель для вращения цилиндров, которые определяли, продолжаете ли вы выполнять свою основную работу или нет. Благодаря правильному профилю движения, медленному разгону и замедлению и повторным испытаниям они смогли использовать двигатель, который превышал эти допустимые значения… намного. |
| Как рассчитать инерцию нагрузки? |
Давайте рассмотрим несколько распространенных примеров, чтобы увидеть, как рассчитывается инерция нагрузки. Во-первых, фундаментальное уравнение для инерции (J) показано ниже.
Уравнение фундаментальной инерции (Дж)
Не беспокойтесь. Существуют упрощенные формы этой формулы.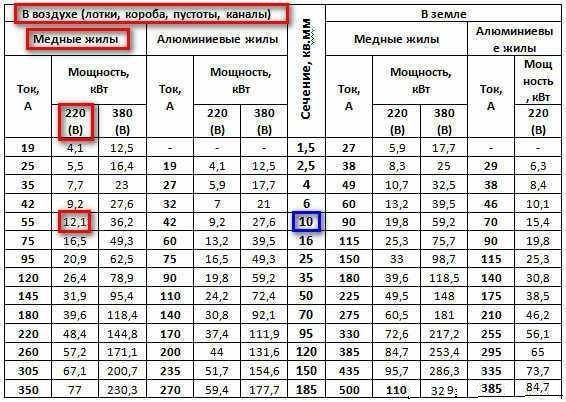 Пять различных упрощенных уравнений для пяти общих нагрузок (объектов) показаны ниже для сплошного цилиндра, полого цилиндра, прямоугольного объекта, прямоугольного объекта со смещенной от центра осью и объекта в линейном движении.
Пять различных упрощенных уравнений для пяти общих нагрузок (объектов) показаны ниже для сплошного цилиндра, полого цилиндра, прямоугольного объекта, прямоугольного объекта со смещенной от центра осью и объекта в линейном движении.
Выберите подходящее уравнение на основе:
- Форма груза (объекта) в движении
- Ось вращения (x или y)
- Подробная информация предоставлена (у вас есть вес груза?)
Например, если указан вес и вы рассчитываете объемный цилиндр, вращающийся вокруг своей оси x, используйте первое уравнение ( Jx ) ниже (с массой « м «). Если масса не указана, но известны диаметр, толщина и плотность материала груза, то инерцию груза можно рассчитать по второму уравнению ( Jx) ниже (с плотностью « p «).
Инерция цилиндра или диска (относительно оси x или y) низкий Цилиндр (по оси x или y)
Инерция прямоугольного объекта (относительно оси x или y)
Инерция прямоугольного объекта со смещенной от центра осью
Инерция объекта в линейном движении
| Единица измерения |
Единицы инерции обычно используются двумя способами: унции-дюйм² и унции-дюйм² . Первое включает гравитацию, второе — только массу. Теоретически инерция является фактором массы, поэтому она не должна включать гравитацию, однако практически мы не можем легко измерить массу на Земле.
Первое включает гравитацию, второе — только массу. Теоретически инерция является фактором массы, поэтому она не должна включать гравитацию, однако практически мы не можем легко измерить массу на Земле.
Восточный двигатель обычно обеспечивает инерцию в унциях на дюйм². Затем, когда мы вычисляем момент ускорения, мы делим общую инерцию на силу тяжести.
Гравитация = 386 дюймов/сек²
- унция-дюйм² = Инерция в зависимости от веса
- унции-в-сек² = инерция на основе массы
Преобразование унций-дюйм² в унции-дюйм-сек²
Для выполнения этих расчетов вам может понадобиться дополнительная информация, например плотность материала. Это необходимо для расчета веса объекта. Больше можно найти с помощью простого онлайн-поиска.
| Пример: расчет инерции нагрузки |
Попробуйте рассчитать инерцию нагрузки для следующего приложения. Для каких частей вам нужно произвести расчет?
Для каких частей вам нужно произвести расчет?
Вам потребуется сложить все значения инерции нагрузки всех компонентов, приводимых в движение двигателем. Это включает в себя груз, ремень и ролики. Вам нужно будет использовать 2 разных уравнения.
Из того, что мы узнали в , вот расчет момента нагрузки.
| Работа с большой инерцией нагрузки? Используйте мотор-редуктор |
Если вы имеете дело с большой инерцией нагрузки, есть простой способ уменьшить ее в геометрической прогрессии. Инерция нагрузки уменьшается на квадрат передаточного отношения. Полученное значение представляет собой инерцию отраженной нагрузки , который представляет собой инерцию нагрузки на валу двигателя (в отличие от инерции нагрузки на валу редуктора).
Если вам интересно узнать больше, вот информационный документ, в котором обсуждается, как использовать редукторы для уменьшения инерции нагрузки. Это специально для шаговых двигателей.
Это специально для шаговых двигателей.
| Где я могу найти «Допустимая инерция нагрузки»? |
Теперь, когда вы рассчитали общее значение инерции нагрузки, как найти двигатель, способный с этим справиться?
Вот пример таблицы допустимой инерции нагрузки для бесколлекторного двигателя серии BLE2 мощностью 200/400 Вт (из нашего каталога). Поскольку мы уже рассчитали максимально допустимые значения инерции нагрузки для каждого передаточного числа, вам не нужно этого делать. Старайтесь не превышать эти значения . Двигатели могут продолжать работать, если эти значения превышены, но это не может быть гарантировано.
Если у вас нет нашего каталога, мы также перечислим Значение допустимой инерции нагрузки на сайте .
Для шаговых двигателей или серводвигателей допустимые значения инерции нагрузки не публикуются , поэтому используйте рекомендуемые значения коэффициента инерции..jpg)
На данный момент это инерция нагрузки. Помните, что инерция нагрузки — это лишь один из трех расчетов, необходимых для правильного определения размера двигателя (не забывайте о крутящем моменте и скорости). В следующем посте «Основы расчета двигателя» я объясню, как инерция нагрузки влияет на другую составляющую крутящего момента — 9.0059 крутящий момент ускорения , который также важен для определения общего требуемого крутящего момента для приложения (и является основной причиной того, почему гоночные велосипеды легче крутят педали, чем обычные велосипеды).
Нужно освежить знания? Вот официальный документ по габаритам двигателя (из последнего поста).
В следующем посте я объясню, как рассчитать момент ускорения, среднеквадратический момент и скорость.
Вот последнее сообщение:
СОВЕТ: Есть ли более простой способ определения размеров двигателей? |
При выборе двигателя следует помнить, что результат зависит от данных. |
 5-23.
5-23. 6 )
6 )  (D 4 — d 4 ) / D
(D 4 — d 4 ) / D 