Угловая скорость | это… Что такое Угловая скорость?

Угловая скорость (синяя стрелка) в одну единицу по часовой стрелке

Угловая скорость (синяя стрелка) в полторы единицы по часовой стрелке

Угловая скорость (синяя стрелка) в одну единицу против часовой стрелки

Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:

,

а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.

Единица измерения угловой скорости, принятая в системах СИ и СГС — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]). В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли просто «вручную», подсчитывая число оборотов за единицу времени.

Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью , определяется формулой:

где  — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) от оси вращения можно считать так: Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.

• В случае плоского вращения, то есть когда все векторы скоростей точек тела лежат (всегда) в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.
• Производная угловой скорости по времени есть угловое ускорение.
• Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю).
• Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчета, однако в разных инерциальных системах отсчета может различаться ось или центр вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
• В случае движения одной единственной точки в трехмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:

, где  — радиус-вектор точки (из начала координат),  — скорость этой точки.  — векторное произведение,  — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы , подходящие по определению, по другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как дает разные для каждой точки, а при вращении абсолютно твёрдого тела по определению угловая скорость его вращения — единственный вектор). При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.

• В случае равномерного вращательного движения (то есть движения с постоянным вектором угловой скорости) декартовы координаты точек вращающегося так тела совершают гармонические колебания с угловой (циклической) частотой, равной модулю вектора угловой скорости.

• При измерении угловой скорости в оборотах в секунду (об/с), модуль угловой скорости равномерного вращательного движения совпадает с частотой вращения f, измеренной в герцах (Гц), то есть в таких единицах . В случае использования обычной физической единицы угловой скорости — радианов в секунду — модуль угловой скорости связан с частотой вращения так: . Наконец, при использовании градусов в секунду связь с частотой вращения будет: .

Связь с конечным поворотом в пространстве

• Пусть поворот, изменяющийся во времени, задан величиной угла и ортом оси конечного поворота в пространстве . Тогда угловая скорость, соответствующая этому повороту, равна

.

• Если поворот задан матрицей поворота , где — символ Кронекера, — символ Леви-Чивиты (суммирование ведется по правилу Эйнштейна от 1 до 3), выражение для элементов которой через и могут быть получены, например, с помощью формулы Родрига, то угловая скорость равна

.

• Если для описания поворота используется кватернион, выражаемый через угол и орт оси поворота как , то угловая скорость находится из выражения .

• В случае, когда поворот описывается с помощью вектора , изменяющегося во времени, обозначим , а также — матрица половинного поворота , — квадрат модуля вектора . Тогда угловая скорость:

.

См. также

• Угловая частота
• Угловое ускорение
• Момент импульса

Литература

• Лурье А. И. Аналитическая механика\\ А. И. Лурье. — М.: ГИФМЛ, 1961. — С. 100-136

Модуль — угловая скорость — Большая Энциклопедия Нефти и Газа, статья, страница 2

Cтраница 2

Если требуется найти модуль угловой скорости тела в определенный момент времени, то для этого, согласно ( 3), достаточно разделить скорость какой-либо точки в этот же момент времени на кратчайшее расстояние от этой точки до мгновенной оси.
 [16]

По каким формулам определяются модули угловой скорости и углового ускорения вращающегося твердого тела.
 [17]

Если с течением времени модуль угловой скорости увеличивается, вектор Р сонаправлен с вектором угловой скорости со, в противном случае — противоположен со.
 [18]

Утверждают даже, что модуль угловой скорости равен ф ( как известно.
 [19]

В ответах приведены не модули угловых скоростей, а проекции угловых скоростей на ось z, перпендикулярную чертежу. Знак, определение которого не входило в условие задачи, дает дополнительную информацию о направлении вращения звена.
 [20]

По этой формуле определяем модуль угловой скорости вращения тела вокруг мгновенной оси.
 [21]

Последнее выражение показывает, что модуль угловой скорости является пределом отношения угла поворота тела к соответствующему промежутку времени при условии, что этот промежуток времени стремится к нулю ( ср.
 [22]

Такой вектор сразу определяет и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси.
 [23]

Последнее выражение показывает, что модуль угловой скорости является пределом отношения угла поворота тела к соответствующему промежутку времени при условии, что этот промежуток времени стремится к нулю ( ср.
 [24]

Строго говоря, это — модуль угловой скорости, сама угловая скорость является векторной величиной.
 [25]

В этой формуле шь со2 — модули угловых скоростей, г, г2 — радиусы начальных окружностей, d, d2 — диаметры начальных окружностей, 2j, 2з — числа зубцов первого и соответственно второго колеса.
 [26]

В этой формуле о1, со2 — модули угловых скоростей, г1; г2 — радиусы начальных окружностей, dlt d2 — диаметры начальных окружностей, Zi, 2 — 2 — числа зубцов первого и соответственно второго колеса.
 [27]

Модуль переносной скорости этой точки равен произведению модуля угловой скорости сой на расстояние РеРг от точки до мгновенной оси переносного вращения плоской фигуры.
 [28]

О г. Легко видеть, что ф с равно модулю угловой скорости со.
 [30]

Страницы:  

   1

   2

   3

   4

Угловая скорость: значение, формула и примеры

Вы слышали о скорости и слышали об углах, но слышали ли вы об угловой скорости? Угловая скорость описывает, насколько быстро объект движется с точки зрения углов, а не с точки зрения расстояний. Это другой взгляд на движение объектов, но в некоторых случаях он может быть очень удобным, и с помощью некоторых простых формул мы действительно можем связать «нормальную» скорость с угловой скоростью. Давайте погрузимся!

Определение угловой скорости

Подобно тому, как мы сначала узнаем о положении и смещении, прежде чем узнать о скорости, мы должны сначала определить угловое положение, чтобы говорить об угловой скорости.

Угловое положение

Угловое положение объекта относительно точки и опорной линии представляет собой угол между этой опорной линией и линией, проходящей через точку и объект.

Это не самое интуитивно понятное определение, поэтому см. иллюстрацию ниже, чтобы получить четкое представление о том, что имеется в виду.

Мы видим, что абсолютные расстояния не имеют значения для углового положения, а только отношения расстояний: мы можем изменить масштаб всей этой картины, и угловое положение объекта не изменится.

Если кто-то идет прямо к вам, его угловое положение по отношению к вам не меняется (независимо от выбранной вами опорной линии).

Угловая скорость

Угловая скорость объекта относительно точки является мерой того, насколько быстро этот объект перемещается в поле зрения точки, в том смысле, насколько быстро изменяется угловое положение объекта.

Угловая скорость объекта по отношению к вам соответствует тому, насколько быстро вы должны поворачивать голову, чтобы смотреть прямо на объект.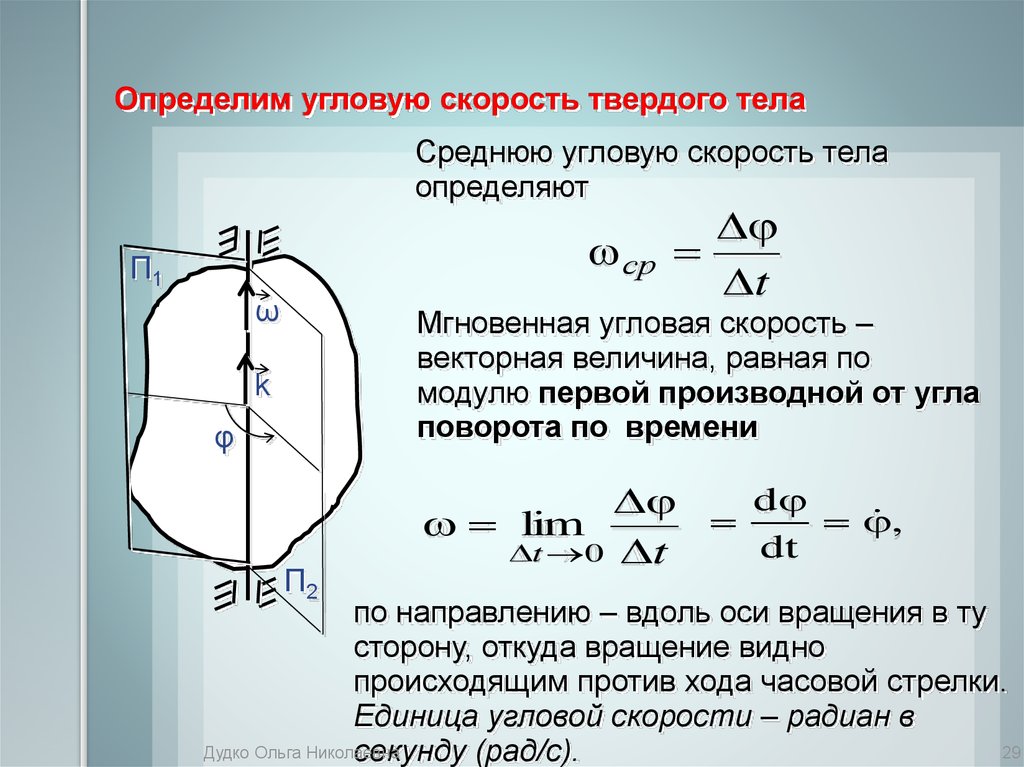 {-1}\). Поскольку угол всегда имеет безразмерную меру, т.е. градусов или радианов, угловая скорость может быть записана следующими способами:

\[\omega=\dfrac{xº}{s}=\dfrac{y\,\mathrm{rad}}{s}=y\dfrac{\mathrm{rad}}{s}\]

Здесь , у нас есть знакомое преобразование между градусами и радианами как \(\dfrac{x}{360}=\dfrac{y}{2\pi}\) или \(y=\dfrac{\pi}{180}x \).

Помните, что градусы могут быть интуитивно понятны, и использовать градусы для выражения углов нормально, но в расчетах (например, при расчете угловых скоростей) всегда следует использовать радианы.

Формула угловой скорости

Давайте рассмотрим несложную ситуацию, предположим, что частица движется вокруг нас по кругу. Этот круг имеет радиус \(r\) (расстояние от нас до частицы), а частица имеет скорость \(v\). Очевидно, что угловое положение этой частицы изменяется со временем из-за ее круговой скорости, и угловая скорость \(\omega\) теперь равна

\[\omega=\dfrac{v}{r}\]

При работе с уравнениями крайне важно использовать радианы в единицах угловой скорости.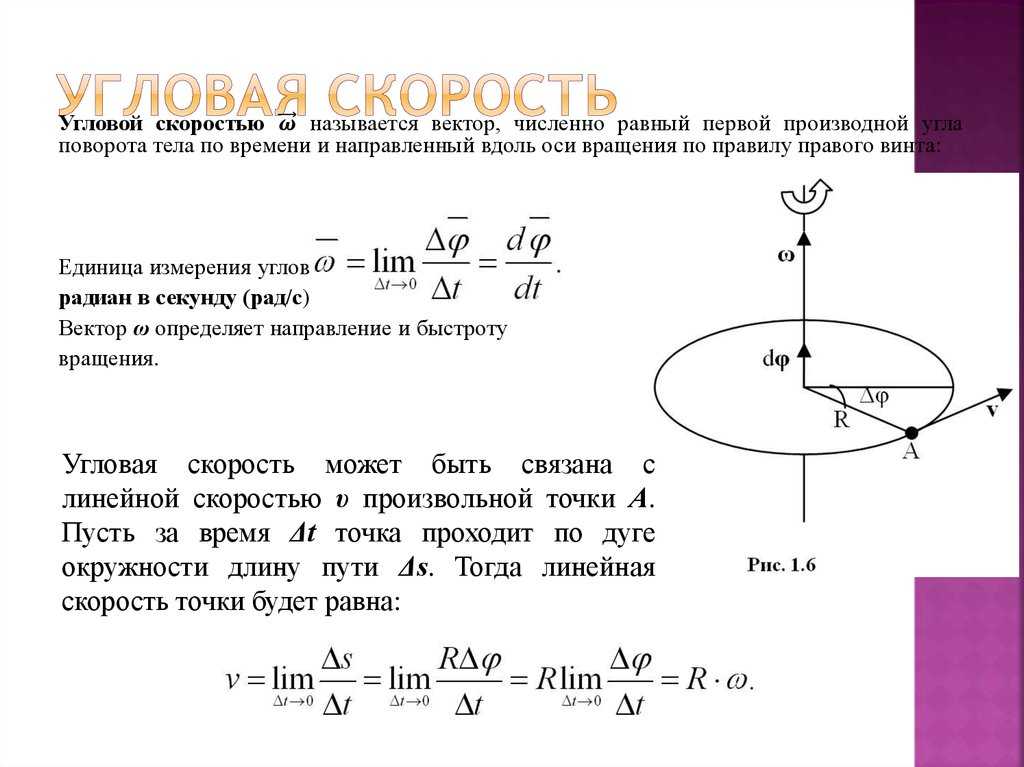 Если вам дана угловая скорость, выраженная в градусах в единицу времени, самое первое, что вы должны сделать, это преобразовать ее в радианы в единицу времени!

Пришло время проверить, имеет ли смысл это уравнение. Во-первых, угловая скорость удваивается, если удваивается скорость частицы, что и ожидалось. Однако угловая скорость также удваивается, если радиус частицы уменьшается вдвое. Это верно, потому что частице нужно будет преодолеть только половину первоначального расстояния, чтобы совершить один полный оборот своей траектории, поэтому ей также потребуется только половина времени (поскольку мы предполагаем постоянную скорость при уменьшении вдвое радиуса).

Ваше поле зрения представляет собой определенный угол (который примерно равен \(180º\) или \(\pi\,\mathrm{rad}\)), поэтому угловая скорость объекта полностью определяет, насколько быстро он движется через ваше поле зрения. зрение. Появление радиуса в формуле угловой скорости является причиной того, что далекие объекты движутся через ваше поле зрения гораздо медленнее, чем близкие.

Преобразование угловой скорости в линейную скорость

Используя приведенную выше формулу, мы также можем рассчитать линейную скорость объекта \(v\) из его угловой скорости \(\omega\) и его радиуса \(r\) следующим образом:

\[v=\omega r\]

Эта формула для линейной скорости является просто манипуляцией предыдущей формулы, так что мы уже знаем, что эта формула логична. Опять же, убедитесь, что в расчетах используются радианы, а также при использовании этой формулы.

В целом можно утверждать, что линейная скорость объекта напрямую связана с его угловой скоростью через радиус круговой траектории, по которой он следует.

Угловая скорость Земли

Вращение Земли вокруг своей оси, ускоренное, Wikimedia Commons CC BY-SA 3.0.

Хорошим примером угловой скорости является сама Земля. Мы знаем, что Земля совершает полный оборот \(360º\) каждые 24 часа, поэтому угловая скорость ω объекта на экваторе Земли относительно центра Земли равна

\[\omega=\ dfrac{360º}{24\,\mathrm{h}}\]

\[\omega=\dfrac{2\pi}{24}\dfrac{\mathrm{rad}}{\mathrm h}\]

Обратите внимание, как мы сразу же перевели в радианы для нашего расчета.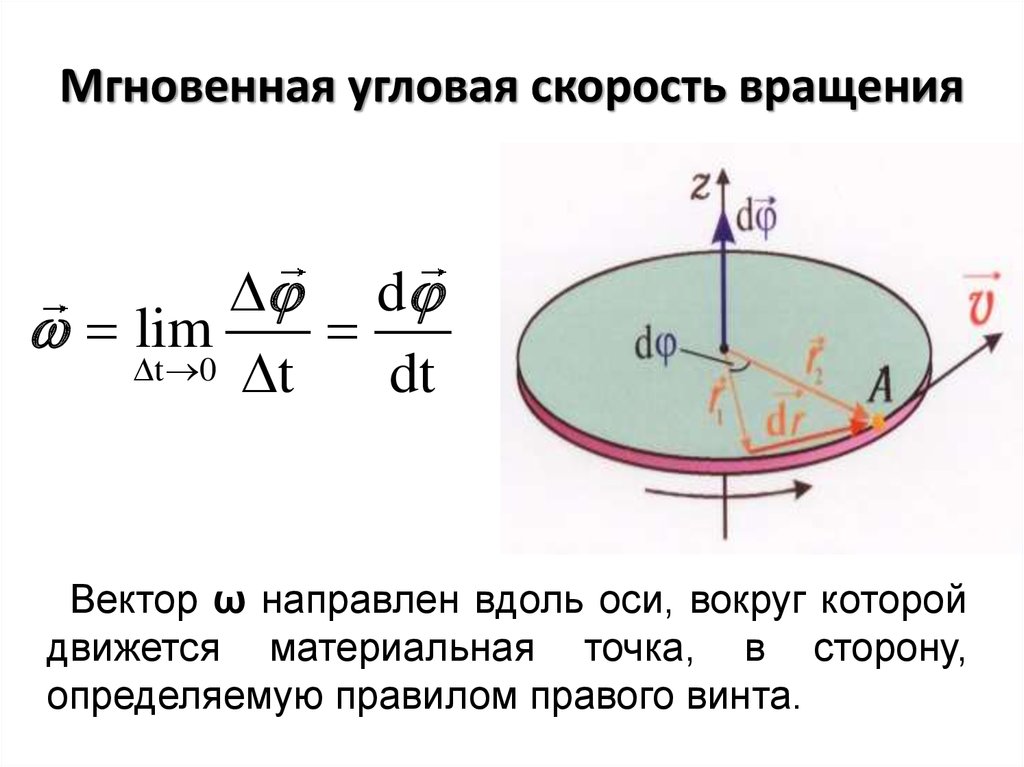

Радиус Земли равен \(r=6378\,\mathrm{км}\), поэтому теперь мы можем рассчитать линейную скорость \(v\) объекта на экваторе Земли, используя формулу, которую мы ввели ранее:

\[v=\omega r\]

\[v=\dfrac{2\pi}{24}\dfrac{\mathrm{rad}}{\mathrm h}·6378\,\mathrm{км} \]

\[v=1670\,\dfrac{\mathrm{km}}{\mathrm h}=464\,\dfrac{\mathrm{m}}{\mathrm s}\]

Угловая скорость Автомобили на кольцевой развязке

Предположим, что круговая развязка в Далласе представляет собой идеальный круг с центром в центре города и радиусом \(r=11\,\mathrm{mi}\), а ограничение скорости на этой кольцевой развязке составляет \(45\,\mathrm{ми/ч}\). Угловая скорость автомобиля, движущегося по этой дороге на предельной скорости относительно центра города, рассчитывается следующим образом: 9{-1}\]

\[\omega=4.1\,\mathrm{rad/h}\]

Если мы хотим, мы можем преобразовать это в градусы:

\[4.1\,\mathrm{rad /h}=\dfrac{235º}{\mathrm{h}}\]

Угловая скорость — основные выводы

• Угловая скорость объекта относительно точки является мерой того, насколько быстро этот объект движется через точка зрения в смысле того, как быстро изменяется угловое положение объекта.
• Единицами угловой скорости являются обратно пропорциональные единицы времени.
  • При записи угловой скорости мы можем использовать градусы в единицу времени или радианы в единицу времени.
  • При вычислениях с углами мы всегда используем радианы.
• Угловая скорость \(\omega\) вычисляется из (линейной) скорости \(v\) и радиуса \(r\) как \(\omega=\dfrac{v}{r}\).
  • Это логично, потому что чем быстрее что-то движется и чем ближе оно к нам, тем быстрее оно перемещается в нашем поле зрения.
• Мы можем рассчитать линейную скорость по угловой скорости и радиусу как \(v=\omega r\).
• Угловая скорость вращения Земли вокруг своей оси равна\(\dfrac{2\pi}{24}\dfrac{\mathrm{rad}}{\mathrm{h}}\).

Круговое движение — Física General

До сих пор мы исследовали задачи, в которых ускорение имело постоянное направление. Одно из наиболее важных движений, круговое, требует, чтобы ускорение изменило направление так, чтобы вектор скорости соответствовал замкнутой криволинейной траектории.

Мы начнем с вычета ускорения для кругового движения, где модуль скорости сохраняется постоянным, чтобы обсудить важные возникающие понятия, такие как угловая скорость . Затем мы перейдем к понятиям собственных компонентов ускорения Внутренних компонентов ускорения и их связи с угловым ускорением .

Равномерное круговое движение

Рис. 44 При круговом движении траектория объекта представляет собой окружность. Как обычно, вектор скорости касается этой окружности.

Равномерное круговое движение подтверждает, что =R\left(\cos(\theta(t))\vec{i}+\sin(\theta(t))\vec{j}\right)\]

Здесь система будет перемещаться по окружности с центром в начале координат и радиусом R, если угол поворота \(\theta\) изменяется со временем, а R остается постоянным. Однако ничто здесь не заставляет движение униформа . Для этого нам нужно рассчитать скорость. Применяя непосредственно определение скорости, получаем

(98)\[\vec{v}=\frac{d\vec{r}}{dt}=R\left(-\sin(\theta(t)) \vec{i}+\cos(\theta(t))\vec{j}\right)\frac{d\theta}{dt}(t)\]

Нетрудно видеть, что этот вектор перпендикулярно вектору положения и касательной к окружности (как и ожидалось для скорости). Теперь, взяв модуль скорости, мы можем заставить его принимать постоянное значение.

(99)\[\vert\vec{v}\vert=R\frac{d\theta}{dt}(t)=cte \Rightarrow \frac{d\theta}{dt}(t)=cte =\omega\]

Глядя на правую часть уравнения. (98) мы видим, что постоянная \(\omega\) представляет собой изменение угла поворота во времени и по этой причине обычно называется угловой скоростью .

Сосредоточившись теперь на левой части уравнения. (98) мы можем наблюдать важную, общую зависимость. Модуль ( линейной ) скорости равен угловой скорости, умноженной на радиус траектории, 92\vec{u}_\rho\end{split}\]

Таким образом, мы видим, что ускорение при равномерном круговом движении всегда равно

Более того, мы видим, что оно пропорционально радиусу и угловой скорости в квадрате.

Внутренние компоненты ускорения

На этом этапе удобно определить общее разложение ускорения, которое дает много информации во время движения. Чтобы разложить ускорение, мы создадим набор осей, который изменяется во время траектории,

• одна из осей указывает направление скорости и, следовательно, касается траектории.

• другие точки оси просто перпендикулярны предыдущей и содержат весь нормальный вклад в ускорение.

Рис. 45 Ускорение разлагается в каждой точке траектории на параллельную (касательную) и перпендикулярную (нормальную) составляющие.

Составляющая ускорения, идущая вдоль направления скорости, называется тангенциальное ускорение , \(\vec{a}_t\), а то, которое указывает в перпендикулярном направлении, называется нормальным ускорением , \(\vec{a}_r\). Они показаны на рис. 45 и вместе составляют полное ускорение.

(103)\[\vec{a}=\vec{a}_r+\vec{a}_t\]

Учитывая, что тангенциальное ускорение указывает в направлении скорости, используя уравнение (88), мы Сразу видно, что направление скорости не меняется вместе с ним, а изменяется ее модуль, 92}{R}\]

и является единственной ответственной за изменение направления вектора скорости. Как видно из уравнения (105) она пропорциональна квадрату линейной скорости и обратно пропорциональна радиусу траектории.