Содержание
Физические основы механики
ЦЕЛЬ РАБОТЫ
Изучение равнопеременного и равномерного прямолинейных движений в поле земного тяготения. Определение ускорения свободного падения.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Основные законы динамики материальных точек — это законы Ньютона. В частности, второй закон Ньютона, математическая запись которого, как известно, имеет вид:
|
|
(1)
|
называют основным уравнением динамики.
Эскиз машины Атвуда показан на рис. 1.
Рис. 1. Эскиз машины Атвуда
Два одинаковых груза с массами М соединены нитью, перекинутой через неподвижный блок. Если на один из грузов положить перегрузок массой m (в виде шайбы), то система приходит в ускоренное движение. Каждый из грузов натягивает участок нити, который, стараясь сократиться, действует на соответствующий груз с силой натяжения Т1 или Т2, а на блок — с силами Т’1 и Т’2. Тогда на каждый груз действует сила тяжести и сила натяжения нити.
Каждый из грузов натягивает участок нити, который, стараясь сократиться, действует на соответствующий груз с силой натяжения Т1 или Т2, а на блок — с силами Т’1 и Т’2. Тогда на каждый груз действует сила тяжести и сила натяжения нити.
Основное уравнение динамики для груза с перегрузком имеет вид:
|
|
(2)
|
а для другого груза (без перегрузка):
|
|
(3)
|
Основное уравнение динамики вращательного движения неподвижного блока имеет вид:
|
|
(4)
|
где SMk — алгебраическая сумма моментов сил, действующих на блок, относительно оси вращения; I — момент инерции блока относительно оси вращения; e — его угловое ускорение.
Если вращение по часовой стрелке считать положительным, то, согласно рис. 1, получим
|
|
(4а)
|
где: R — радиус блока; Мтр — момент силы трения.
Будет считать, что нить невесомая, нерастяжимая и не скользит по блоку. Из условия невесомости нити следует:
|
|
(5)
|
Из условия нерастяжимости нити следуют равенства модулей перемещений, скоростей и ускорений грузов и нити:
|
|
(6)
|
Наконец, в отсутствие скольжения нити по блоку, ускорение грузов и нити а равно модулю тангенциального ускорения точек обода блока:
или
|
|
(7)
|
Проецируя уравнения (2) и (3) на ось у, направленную вертикально вверх, получим с учетом формул (5), (6) и (7) систему уравнений, к которой присоединим уравнение (4а):
|
|
(8)
|
Умножая первое из уравнений (8) на (-1), и складывая все уравнения (8), получим
|
|
(9)
|
В данной лабораторной установке момент сил трения настолько мал, что выполняется неравенство
|
|
(10)
|
Кроме того, в лабораторной установке величина момента инерции I блока такова, что справедливо другое неравенство:
|
|
(11)
|
Пренебрегая малыми величинами, из уравнения (9) получим формулу для расчёта ускорения а системы грузов под действием перегрузка массой m:
|
|
(12)
|
а модули сил натяжения нити Т1 и Т2 по обе стороны блока равны:
|
|
(13)
|
Можно сказать, что равенство (13) выполняется при двух предположениях (10) и (11).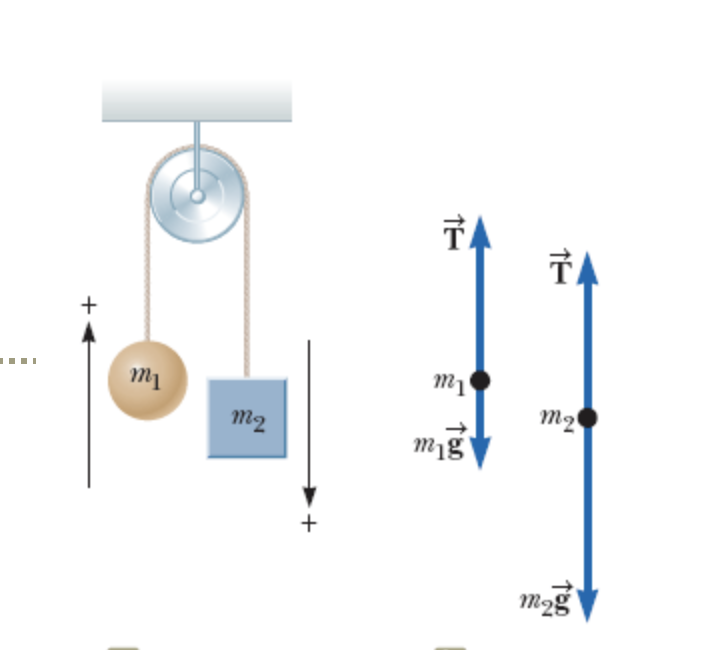
Равноускоренное движение системы грузов вдоль оси у описывается уравнениями движения произвольной точки системы:
где у1, v1 — начальные параметры.
Исключая из этих уравнений время t, при условии v1=0, получим
|
|
(14)
|
Система грузов перемещается на величину sy=L1, двигаясь равноускоренно под действием перегрузка массой m с ускорением, которое определяется формулой (12).
В точке с координатой у2 и скоростью v2 перегрузок подхватывается столиком, и система грузов движется равномерно, перемещаясь на величину L2 за время t, измеряемое миллисекундомером экспериментальной установки. Подставляя в равенство (14) формулу
Подставляя в равенство (14) формулу
получим
|
|
(15)
|
При изменении L2 меняется время t, измеряемое секундомером, но ускорение а должно оставаться неизменным.
С помощью формулы (15) найдём расчётную формулу для величины ускорения а грузов с перегрузком:
|
|
(16)
|
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
К основанию 1 экспериментальной установки (см.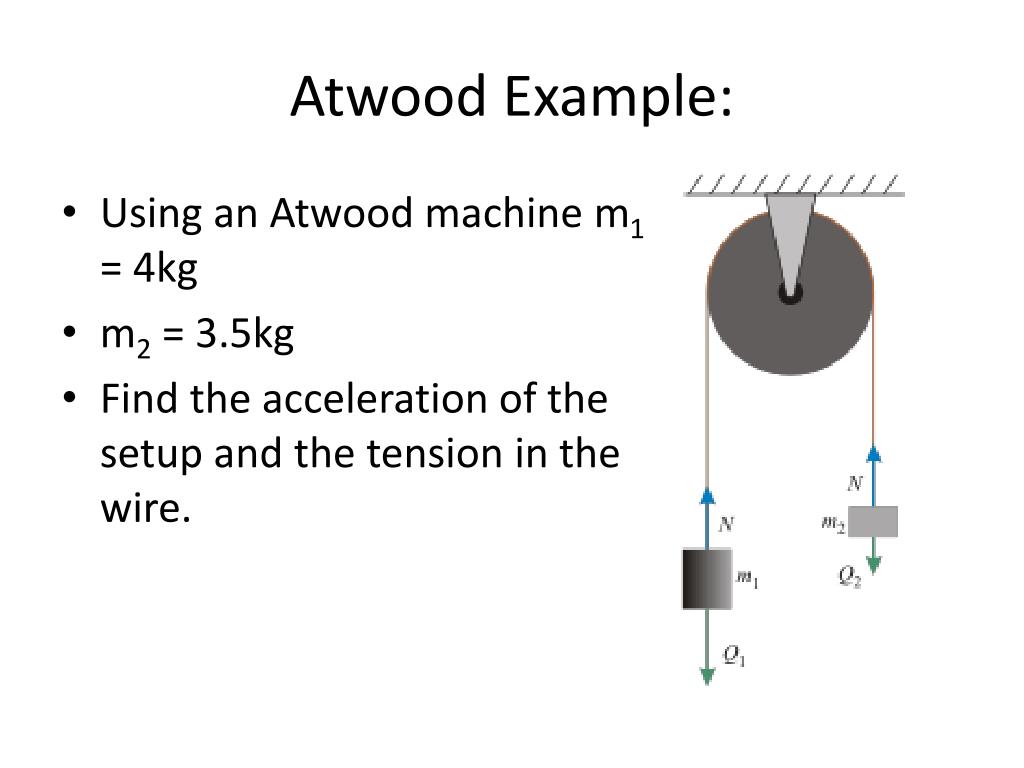 рис. 2), которая стоит на ножках 2, прикреплена вертикальная стойка 3. К стойке крепится кронштейн 4, который может перемещаться вдоль стойки. На кронштейне находится столик для снятия перегрузка.
рис. 2), которая стоит на ножках 2, прикреплена вертикальная стойка 3. К стойке крепится кронштейн 4, который может перемещаться вдоль стойки. На кронштейне находится столик для снятия перегрузка.
Рис. 2. Схема экспериментальной установки
На верхнем конце стойки находится неподвижный блок 5. Для наблюдения ускоренного движения грузов на правый груз 6 помещают перегрузок 7 и поднимают их в верхнее положение путем нажатия кнопок «+» или «-». Значение массы перегрузка показывается в окне «масса После нажатия кнопки «ПУСК» начинается ускоренное движение грузов и перегрузка до того момента, когда столик 4 подхватит перегрузок. Одновременно включается миллисекундомер, измеряющий время равномерного движения грузов до остановки. Итак, во время равноускоренного движения грузы проходят расстояние L1 (см. рис. 1) и приобретают скорость v2, с которой, двигаясь равномерно, проходят расстояние L2 за время t, измеренное миллисекундомером в секундах и показанное в окне «время».
Для подготовки прибора к следующему измерению нажимают кнопку «СБРОС».
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Упражнение 1. ИЗМЕРЕНИЕ УСКОРЕНИЯ ГРУЗОВ
1. Измерьте расстояние L с помощью линейки и занесите результат в таблицу измерений 1. Цена деления линейки 1 см.
Обратите внимание на необходимость записывать данные в системе СИ, то есть, в метрах.
Таблица 1
|
m=… кг
|
L=… м
|
L2=… м
| |
|
№ наблюдения
|
Время ti, с
| ||
|
1
| |||
|
2
| |||
|
3
| |||
|
4
| |||
|
5
| |||
2. Выберите значение массы перегрузка m и занесите ее значение в таблицу 1. Выбор производится мышкой с помощью нажатия ей на кнопки со значками «+» или «-». Значение массы перегрузка показывается в окне «масса». Оптимальным для выбора является значение массы от 5 до 10 г. Учтите, что масса в данной работе определена при взвешивании тел на весах с точностью, равной половине цены деления весов. Приборная погрешность весов составляла 0.1 г.
Выберите значение массы перегрузка m и занесите ее значение в таблицу 1. Выбор производится мышкой с помощью нажатия ей на кнопки со значками «+» или «-». Значение массы перегрузка показывается в окне «масса». Оптимальным для выбора является значение массы от 5 до 10 г. Учтите, что масса в данной работе определена при взвешивании тел на весах с точностью, равной половине цены деления весов. Приборная погрешность весов составляла 0.1 г.
Обратите внимание на необходимость записывать данные в системе СИ, то есть, в килограммах.
3. Установите, взяв мышкой, кронштейн со столиком на некотором расстоянии L2 от нижнего фиксатора расстояний. Возможные пределы варьирования расстояния от 12 до 25 см. Измерьте установленное расстояние L2 по линейке, взяв отсчёт по красной черте. Результаты измерения запишите в таблицу 1 результатов измерений 1. Цена деления линейки 1 см.
Обратите внимание на необходимость записывать данные в системе СИ, то есть, в метрах.
4. Нажмите кнопку «ПУСК».
5. После остановки грузов запишите в таблицу 1 время t равномерного движения грузов, измеренное миллисекундомером и показанное на табло «время». Время необходимо записывать в системе СИ, то есть в секундах. Погрешность миллисекундомера составляет 0.001 с.
6. Нажмите кнопку «СБРОС».
7. Повторите пункты 3 — 5 ещё четыре раза, не меняя расстояние L2.
8. Вычислите среднее значение времени <t>. Результат занесите в таблицу расчетов 2.
Таблица 2
|
№ наблюдения
|
ti
|
ti-<t>
|
(ti-<t>)2
|
|
1
| |||
|
2
| |||
|
3
| |||
|
4
| |||
|
5
| |||
|
Суммы
|
Sti=…
|
S(ti-<t>)2
| |
|
<t>=…
|
s=…
| ||
|
E=
|
9. Найдите отклонения каждого из пяти измерений ti от среднего значения времени <t>.
Найдите отклонения каждого из пяти измерений ti от среднего значения времени <t>.
10. Возведите в квадрат каждое отклонение и просуммируйте квадраты отклонений.
11. Рассчитайте среднее квадратичное отклонение s, применив для его расчёта формулу для выборочной оценки S(<t>) стандартного отклонения результата измерения по формуле из теории погрешностей
12. Умножив это значение среднего квадратичного отклонения на коэффициент Стьюдента, найдём полуширину доверительного интервала в определении времени
где tP(n) — коэффициент Стьюдента, соответствующий вероятности Р и числу степеней свободы n=n-1.
Для n=5 измерений при рекомендуемой доверительной вероятности P=0.9 имеем из таблицы коэффициентов Стьюдента t0.9(5-1)=2.13.
13. Приборная погрешность в определении времени в нашем случае значительно меньше случайной, поэтому приборная погрешность в определении времени в данном случае не учитывается.
Тогда результат измерения времени t запишем в виде
14. Произведите расчет относительной погрешности в определении времени Et (в процентах) по формуле:
15. Приборная погрешность в определении расстояний уже не может быть отброшена, так как случайной погрешности здесь нет, Тогда для расстояний L и L2 имеем приборные погрешности, равные половине цены деления линейки
16. Ускорение грузов а рассчитывается по формуле (16), в которую подставляется среднее значение времени <t> и измеренные линейкой значения расстояний L и L2.
17. Относительная погрешность в определении ускорения найдётся по формуле:
18. Результат измерения ускорения а запишется в виде
Упражнение 2. ИЗМЕРЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ
19. Определите величину ускорения свободного падения g по формуле
Определите величину ускорения свободного падения g по формуле
При этом значение массы грузов принять равным M=90 г.
20. Полуширину доверительного интервала Dg найдите с помощью формулы
Значения погрешностей в определении масс в данной работе принять равными приборной погрешности при их взвешивании:
21. Оформите отчёт по работе.
ВЫПОЛНЕНИЕ ЛАБОРАТОРНОЙ РАБОТЫ
На рис.3 представлена реальная лабораторная установка, используемая для выполнения данной работы.
Рис.3. Лабораторная установка «Машина Атвуда»
После ознакомления с принципом работы установки необходимо проделать работу на виртуальной лабораторной установке, представленной в правом окне. В процессе выполнения измерений можно свернуть-развернуть окно с описанием лабораторной работы либо свернуть-развернуть окно с лабораторной установкой.
После окончания измерений следует сохранить результаты работы. Для этого необходимо нажать на клавишу или. После этого будет предложено сохранить результаты в файле, имя которого — название лабораторной работы (имя файла изменять не рекомендуется), месторасположение — рабочий стол (можно изменить место сохранения файла). Так как результаты сохраняются в формате html, в дальнейшем вы можете просмотреть результаты, открыв сохраненный файл, а также можете отправить файл на проверку правильности выполнения лабораторной работы преподавателю.
Для этого необходимо нажать на клавишу или. После этого будет предложено сохранить результаты в файле, имя которого — название лабораторной работы (имя файла изменять не рекомендуется), месторасположение — рабочий стол (можно изменить место сохранения файла). Так как результаты сохраняются в формате html, в дальнейшем вы можете просмотреть результаты, открыв сохраненный файл, а также можете отправить файл на проверку правильности выполнения лабораторной работы преподавателю.
РЕКОМЕНДАЦИИ
по оформлению отчета по лабораторным работам (физика)
1. Отчет оформляют в электронном виде в редакторе Word
2. Объем отчета составляет 2-3 страницы.
3. В отчете необходимо указать:
3.1 Фамилию, имя, отчество студента;
3.2 Номер группы;
3.3 Дисциплину;
3.4 Фамилию, имя, отчество преподавателя;
4. Рекомендуемая структура отчета:
4.1 Название работы;
4.2 Цель работы;
4.3 Таблицы измерений и таблицы расчетов, сохраненные в виде отдельного файла.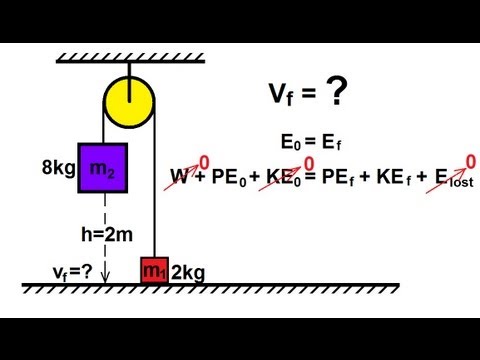
4.5 Формулы и законы, используемые для расчетов;
4.6 Результаты расчетов, не вошедшие в таблицу расчётов;
4.7 Выводы, которые можно сделать из работы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется системой отсчета?
2. Дайте определение материальной точки.
3. Сравните понятия пути и перемещения.
4. Дайте определения средней и мгновенной скоростей.
5. Дайте определения среднего и мгновенного ускорений.
6. Укажите формулы, связывающие кинематические величины при равноускоренном прямолинейном движении.
7. Дайте определение силы.
8. Что характеризует масса тела?
9. Сформулируйте основные законы динамики — законы Ньютона.
10. Какая система тел называется изолированной?
11. Сформулируйте законы сохранения импульса и полной механической энергии системы.
12. Какое движение тела называется свободным падением?
13. Как изменится ускорение свободного падения при подъеме с уровня моря на высоту h=10 км? Радиус Земли R3=6 370 км.
14. При каком условии ускорения тел, используемых в машине Атвуда, одинаковы по модулю?
Лабораторная экспериментальная площадка для школьников
Автор: Шипицина Ирина Александровна. Дата публикации: .
Данная работа посвящена экспериментальной проверке законов Ньютона — важнейших законов классической механики. В данной работе вы проведете серию экспериментов по исследованию прямолинейного равномерного и равноускоренного движения тел на воздушном треке. Познакомитесь с методами описания процесса движения и его регистрации, а также познакомитесь с методами математического анализа результатов эксперимента. Полученные в опыте данные вы сравните с теоретическим описанием на основе законов Ньютона, и в результате сделаете выводы об их применимости для описания движения тел.
Теоретический минимум: система отсчёта, траектории, путь, равномерное прямолинейное движение, скорость, мгновенная скорость, средняя скорость, ускорение, прямолинейное равноускоренное движение, ускорение свободного падения, сила, сила тяжести, сила трения, первый закон Ньютона, инерциальная система отсчёта, неинерциальная система отсчёта, второй закон Ньютона, масса, принцип суперпозиции сил, равнодействующая сила.
Лабораторная работа рекомендуется для учащихся 9, 10 классов.
Автор: Шипицина Ирина Александровна. Дата публикации: .
Данная работа посвящена экспериментальной проверке законов сохранения импульса и энергии — фундаментальных законов физики. В данной работе рассматривается частный случай этих законов, описывающий движение тел и их взаимодействие в рамках классической механики. В данной работе вы проведете серию экспериментов по исследованию прямолинейного движения тел на воздушном треке при наличии и отсутствии внешних воздействий, а также исследуете процессы столкновения нескольких тел. Вы узнаете, как описать движение тел и их взаимодействие, использовав такие теоретические понятия как импульс и энергия. На основе полученных экспериментальных данных вы сделаете выводы о применимости законов сохранения импульса и полной механической энергии тел при их движении и взаимодействии.
Теоретический минимум: система отсчёта, траектории, путь, равномерное прямолинейное движение, скорость, мгновенная скорость, средняя скорость, ускорение, прямолинейное равноускоренное движение, ускорение свободного падения, сила, сила тяжести, сила трения, первый закон Ньютона, инерциальная система отсчёта, неинерциальная система отсчёта, второй закон Ньютона, масса, принцип суперпозиции сил, равнодействующая сила, импульс, закон сохранения импульса, кинетическая энергия, закон сохранения кинетической энергии, упругое столкновение, неупругое столкновение.
Лабораторная работа рекомендуется для учащихся 9, 10 классов.
Автор: Шипицина Ирина Александровна. Дата публикации: .
Теоретический минимум: .
Лабораторная работа рекомендуется для учащихся ___ классов.
Автор: Шипицина Ирина Александровна. Дата публикации: .
Дата публикации: .
В лабораторной работе на примере маятника Максвелла Вы рассмотрите законы поступательного и вращательного движения. На основе законов динамики и законов сохранения механической энергии Вы сможете установить зависимость момента инерции маятника Максвелла, ускорений его поступательного и вращательного движений, определить зависимость энергии диссипации от числа колебаний маятника.
Теоретический минимум: поступательное движение, вращательное движение, инерция, момент инерции, поступательная скорость, угловая скорость, ускорение, центростремительное ускорение, колебания, потенциальная энергия, кинетическая энергия, закон сохранения механической энергии.
Лабораторная работа рекомендуется для учащихся 11 классов.
Автор: Шипицина Ирина Александровна. Дата публикации: .
Данная работа познакомит Вас с понятием центробежной силы. Вам будет предложено измерить центробежную силу, действующую на вращающееся тело, и выяснить, как зависит эта сила от массы тела, расстояния до оси вращения и частоты вращения.
Вам будет предложено измерить центробежную силу, действующую на вращающееся тело, и выяснить, как зависит эта сила от массы тела, расстояния до оси вращения и частоты вращения.
Теоретический минимум: вращательное движение, угловая скорость, частота вращения, период вращения, угловое ускорение, касательное (линейное) ускорение, момент силы, момент инерции, момент импульса.
Лабораторная работа рекомендуется для учащихся 10 классов.
Автор: Шипицина Ирина Александровна. Дата публикации: .
В данной работе Вы изучите гармонические колебания на примере пружинного маятника. Измерив периоды собственных колебаний пружинного маятника, найдёте коэффициенты жёсткости нескольких пружин, проверите зависимость периода и частоты колебаний от массы груза и коэффициента жёсткости пружины. В дополнительном задании Вы проверите формулы для жёсткости систем пружин при последовательном и параллельном соединении.
Теоретический минимум: закон Гука, деформация, упругая деформация, коэффициент упругости (жёсткости), сила упругости, сила тяжести, второй закон Ньютона, ускорение, свободные колебания, гармонические колебания, частота колебаний, циклическая (круговая) частота колебаний, собственная частота, период колебаний.
Лабораторная работа рекомендуется для учащихся 11 классов.
Автор: Шипицина Ирина Александровна. Дата публикации: .
Выбрав данную лабораторную работу в качестве исследования, у Вас будет возможность изучить свободные затухающие колебания, определить амплитудно-частотные характеристики вынужденных механических колебаний, а также быть свидетелем такого явления, как резонанс на примере крутильного маятника Поля.
Теоретический минимум: колебания, механические колебания, внутренние силы, внешние силы, свободные колебания, гармонические колебания, амплитуда, период, частота, циклическая (круговая) частота, собственная частота, фаза, затухающие колебания, вынужденные колебания, резонанс, маятник Поля.
Лабораторная работа рекомендуется для учащихся 11 классов.
Автор: Шипицина Ирина Александровна. Дата публикации: .
Данная лабораторная работа посвящена измерению скорости звука в газах при помощи трубки Кундта. При определенной частоте и амплитуде напряжения, подаваемого на динамик, в трубе возникает звучание, громкость которого зависит от положения поршня. При медленном перемещении поршня от динамика Вы заметите, что громкость периодически возрастает и падает. У Вас будет возможность «увидеть» стоячую акустическую волну.
Теоретический минимум: скорость звука, волна, длина волны, частота, колебания, период, скорость, продольная волна, поперечная волна, стоячие волны, амплитуда, пучность, узел.
Лабораторная работа рекомендуется для учащихся 9 классов.
Автор: Шипицина Ирина Александровна. Дата публикации: .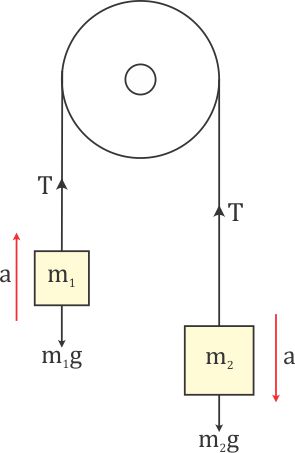
Лабораторная работа предполагает ознакомление с теоретическими основами работы тепловых машин и, в частности, тепловых насосов. Тепловым насосом называют машину, основной целью которой является передача тепла от более нагретого тела холодному при совершении механической работы. Экспериментальная установка представляет собой модель теплового насоса компрессорного типа, на примере которой можно разобрать принцип работы и устройство тепловых насосов и определить эффективность предложенного теплового насоса в зависимости от внешних параметров.
Теоретический минимум: температура, внутренняя энергия, теплопроводность, количество теплоты, удельная теплоёмкость, закон сохранения и превращения энергии, агрегатное состояние вещества, жидкость, газ, парообразование, испарение, конденсация, кипение, температура кипения, удельная теплота парообразования, кпд (коэффициент полезного действия) теплового двигателя (насоса).
Лабораторная работа рекомендуется для учащихся 8, 10 классов.
Автор: Шипицина Ирина Александровна. Дата публикации: .
Двигатель Стирлинга является частным случаем теплового двигателя — двигателя, превращающего тепловую энергию в механическую. Выполняя данную лабораторную работу, юные экспериментаторы имеют возможность ознакомиться с 1-м и 2-м началом термодинамики, наглядно увидеть протекание основных термодинамических процессов, а также понять принцип работы тепловых машин, который является единым для всех тепловых двигателей.
Теоретический минимум: температура, внутренняя энергия, теплопроводность, количество теплоты, удельная теплоёмкость, молекулярно-кинетическая теория, закон сохранения и превращения энергии, первый закон термодинамики, второй закон термодинамики, работа, тепловой двигатель, кпд (коэффициент полезного действия) теплового двигателя, цикл Карно, термодинамическая система, изолированная система, изотермический процесс, изобарный процесс, изохорный процесс, адиабатный процесс, уравнение теплового баланса, нагреватель, холодильник.
Лабораторная работа рекомендуется для учащихся 10 классов.
Автор: Шипицина Ирина Александровна. Дата публикации: .
Теоретический минимум: температура, внутренняя энергия, теплопроводность, количество теплоты, удельная теплоёмкость, молекулярно-кинетическая теория, закон сохранения и превращения энергии, первый закон термодинамики, второй закон термодинамики, работа, тепловой двигатель, кпд (коэффициент полезного действия) теплового двигателя, цикл Карно, термодинамическая система, изолированная система, изотермический процесс, изобарный процесс, изохорный процесс, адиабатный процесс, уравнение теплового баланса, нагреватель, холодильник.
Лабораторная работа рекомендуется для учащихся 10 классов.
Автор: Шипицина Ирина Александровна. Дата публикации: .
Теоретический минимум:
Лабораторная работа рекомендуется для учащихся 10 классов.
Автор: Шипицина Ирина Александровна. Дата публикации: .
Теоретический минимум:
Лабораторная работа рекомендуется для учащихся 10 классов.
Автор: Шипицина Ирина Александровна. Дата публикации: .
Теоретический минимум:
Лабораторная работа рекомендуется для учащихся __ классов.
Автор: Шипицина Ирина Александровна. Дата публикации: .
Исследование зависимости напряженности электрического поля между пластинами конденсатора от разности потенциалов, подаваемой на пластины, и расстояния между пластинами. Экспериментальное решение задачи по определению диэлектрической проницаемости материала, помещенного между пластинами конденсатора.
Теоретический минимум:
Лабораторная работа рекомендуется для учащихся __ классов.
Автор: Шипицина Ирина Александровна. Дата публикации: .
Данная лабораторная работа направлена на ознакомление с правилами Кирхгофа: на нескольких примерах Вы научитесь применять правила Кирхгофа при расчете токов в электрических цепях разной степени сложности.
Теоретический минимум:
Лабораторная работа рекомендуется для учащихся 8 классов.
Автор: Шипицина Ирина Александровна. Дата публикации: .
Получение характерных зависимостей тока, проходящего через элемент электрической цепи от подаваемого на него напряжения для резистора, лампы накаливания, диода.
Теоретический минимум:
Лабораторная работа рекомендуется для учащихся __ классов.
Автор: Шипицина Ирина Александровна. Дата публикации: .
Цель данной работы – экспериментальная проверка теории, описывающей временные зависимости в процессе зарядки и разрядки конденсатора. Для её достижения вам предстоит собрать электрическую схему, позволяющую заряжать от источника постоянного напряжения и разряжать конденсатор, регистрируя временную зависимость тока при помощи амперметра и секундомера.
Теоретический минимум:
Лабораторная работа рекомендуется для учащихся __ классов.
Автор: Шипицина Ирина Александровна. Дата публикации: .
Данная работа позволяет подробно изучить работу электротрансформатора. Вам предстоит собрать схему и исследовать работу трансформатора в трех основных режимах: режим холостого хода, режим короткого замыкания и режим работы под нагрузкой, варьируя входное напряжение, число витков в катушках и тип сердечника и сравнивая полученный результат с теоретическим расчетом.
Теоретический минимум: трансформатор, первичная и вторичная обмотка, сердечник, коэффициент трансформации, повышающий трансформатор, понижающий трансформатор, ток, напряжение, сопротивление, мощность, переменное напряжение, индуктивность, магнитное поле, магнитный поток, закон электромагнитной индукции, закон Фарадея, токи Фуко, электрическая схема, режим холостого хода, режим короткого замыкания, рабочий режим трансформатора.
Лабораторная работа рекомендуется для учащихся 9 классов.
Автор: Шипицина Ирина Александровна. Дата публикации: .
В этой работе вы экспериментально определите элементы земного магнитного поля: склонение, наклонение и числовое значение горизонтальной составляющей, которые полностью характеризуют магнитное поле Земли в данном месте.
Теоретический минимум:
Лабораторная работа рекомендуется для учащихся __ классов.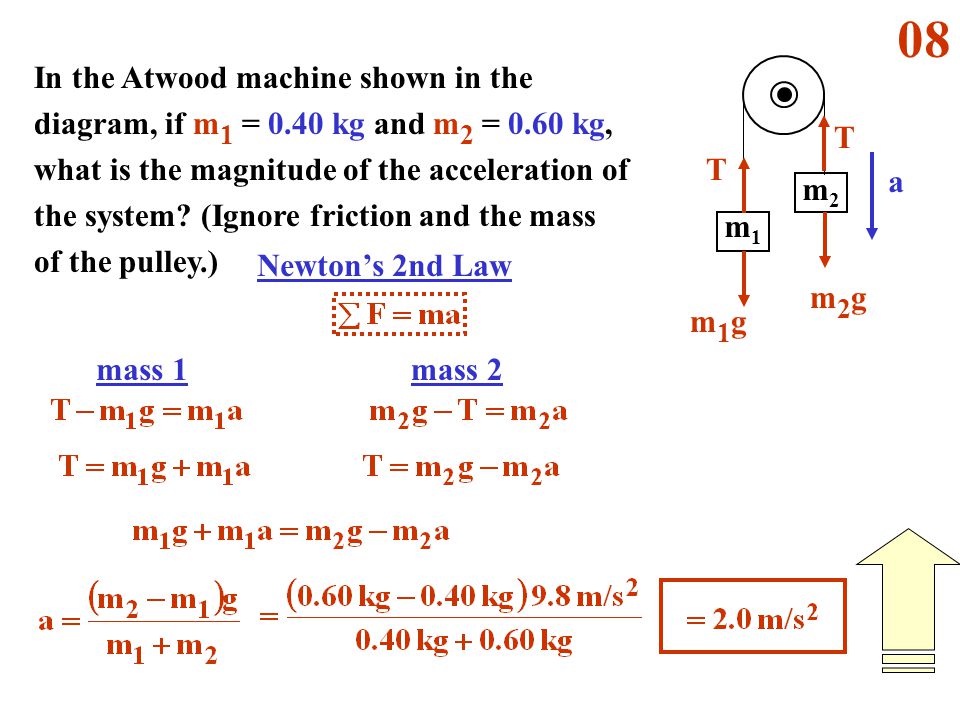
Идеальная машина Этвуда | Carolina.com
Идеальная машина Этвуда | Каролина.com
Моя учетная запись
Войдите или зарегистрируйтесь сейчас, чтобы максимально сэкономить и получить доступ к информации профиля, истории заказов, отслеживанию, спискам покупок и многому другому.
Авторизоваться
Завести аккаунт- Обслуживание и поддержка
Свяжитесь с нами
Наша служба поддержки клиентов работает с 8:00 до 18:00 по восточноевропейскому времени с понедельника по пятницу. Онлайн-чат доступен с 8:00 до 17:30 по восточному времени с понедельника по пятницу.
- Телефон:
- 800.334.5551
- Факс:
- 800.222.7112
- Электронная почта:
- Электронная почта
Обслуживание клиентов
Подробнее Обслуживание и поддержка
Международные продажи и обслуживание
Мы обслуживаем преподавателей более чем в 170 странах мира.
 Создать предложение
Создать предложение
запросите на нашем веб-сайте или свяжитесь с нашим международным отделом продаж.Международная информация для заказа
Покупки
СпискиВойдите или зарегистрируйтесь сейчас, чтобы максимально сэкономить и получить доступ к информации профиля, истории заказов, отслеживанию, спискам покупок и многому другому.
Авторизоваться
Завести аккаунт- Быстрый
Заказать
Эмметт Кокс
Координатор по управлению продуктами для физических наук
Сентябрь 2015 г.
Машина Этвуда или машина Этвуда — это стандартная задача о динамических силах, которая обычно изучается на первом курсе физики.
Машина Этвуда представляет собой просто одиночную фиксированную систему шкивов, установленную в качестве противовеса, как показано на рис. 1. Цель задачи — решить уравнение, определяющее ускорение ( a ) системы.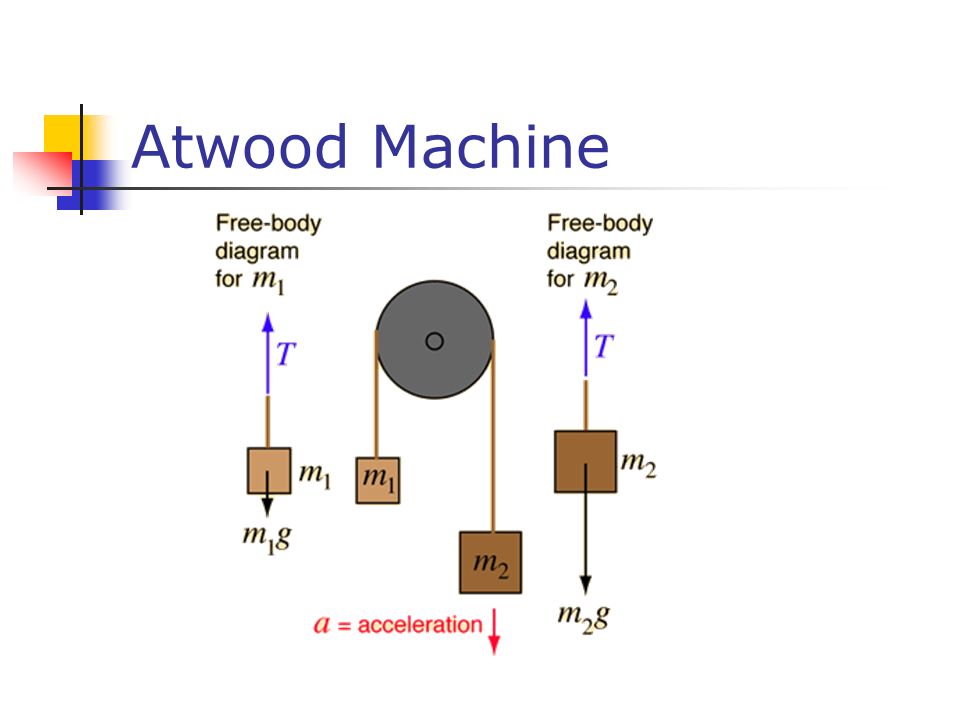 Эта задача — идеальный способ познакомить студентов-физиков с более сложными задачами и помочь им применить предварительные знания о втором законе Ньютона, диаграммах свободного тела и кинематике.
Эта задача — идеальный способ познакомить студентов-физиков с более сложными задачами и помочь им применить предварительные знания о втором законе Ньютона, диаграммах свободного тела и кинематике.
В зависимости от трассы сложность решения зависит от большего количества переменных, таких как трение или масса шкива. Для простейшего случая сделаны следующие допущения:
- Трение игнорируется.
- Масса струны и шкива не учитывается.
- Струна неэластична.
Чтобы найти решение, изучите диаграмму свободного тела:
Рисунок 1
Это идеальная система, в которой сам блок не имеет массы, а натяжение каната везде одинаково. Масса m 1 больше, чем масса m 2 , указанная математическим выражением m 1 >м 2 .
Вес массы m 1 , который равен m 1 г, ускоряет систему, так как масса m 1 падает, а масса m 2 поднимается.
G — ускорение свободного падения, 9,8 м/с 2 . Символы m 1 и m 2 обозначают массу в килограммах. T – напряжение в ньютонах. Сила измеряется в ньютонах, где 1Н = 1 кг x м/с 2 .
Сумма сил на массу m 1 определяется как:
м 1 а = м 1 г – Т
Сумма сил на массу m 2 определяется как:
м 2 а = Т — м 2 г
Обратите внимание, что положительное ускорение назначается направлению движения, а не направлению вверх. Поскольку напряжение T присутствует в обоих уравнениях, решите оба уравнения для T и установить их равными друг другу.
T = m 1 g — m 1 a
T = m 2 a 90 058 + м 1 иОбъедините одинаковые члены и найдите ускорение a .
m 1 g — m 1 a = m 2 a + m 2 g
м 1 а + м 2 а = м 1 г — м 2 г
а( 90 058 м 1 + м 2 ) = г (м 1 — м 2 )Значение для a можно найти, подставив 9,8 м/с 2 вместо g , ускорение свободного падения и значения масс m 1 и m 2 , которые можно измерить.
Измерить ускорение непосредственно с помощью секундомера сложно. Однако учащиеся могут использовать свои знания уравнения кинематики, чтобы предсказать время, когда масса m 1 достигнет земли. Проверьте решение, создав систему, в которой m 2 лежит на земле в исходном положении.
Используйте одно из уравнений кинематики, чтобы найти время, за которое масса m 1 опустится на землю.
В зависимости от доступных ресурсов и оборудования, вы можете организовать этот эксперимент несколькими способами, и это отличная исследовательская деятельность для студентов, чтобы разработать эксперимент для проверки своих результатов. Если ваш класс оснащен программным обеспечением, фотодатчиками или датчиками движения, вы можете напрямую измерить ускорение. Следующая процедура может помочь вам начать работу.
Измерение ускорения
Во время этой процедуры вы подтвердите ускорение, рассчитав время, за которое машина Этвуда пройдет весь диапазон движения и остановится с помощью базового шкива. Прежде чем начать, вы должны рассчитать величину трения в системе.
Материалы
- Строка
- Рулетка или измерительная линейка
- Шкив с низким коэффициентом трения
- Таймер или секундомер
Этап 1
Рассчитайте ускорение системы с поправкой на силу трения в шкиве.

Без учета трения ускорение в системе выражается уравнением:Шаг 2
Соберите машину Этвуда, используя шкив с низким коэффициентом трения, веревку и несколько грузов. Грузы должны иметь возможность свободно перемещаться при вращении шкива, не сталкиваясь друг с другом. Подвесьте шкив на кольцевой подставке или другой опоре. Масса м 2 должен лежать на полу. Результаты будут лучше, когда масса m 1 имеет более длинное падение.
Шаг 3
Запишите значения масс m 1 и m 2 , а также измерьте и запишите высоту массы m 1 от основания груза до пола.
Шаг 4
Рассчитайте время, необходимое системе для выполнения полного диапазона движения. Если система начинается с более легкой массы, m 2 , опирается на пол, а h — расстояние от нижней части более тяжелой массы, м 1 , до пола, измеренное в метрах, то можно найти положение большей массы как функцию времени используя это кинематическое уравнение:
Где a — ускорение, рассчитанное для системы, t, — время, за которое масса m 1 достигает пола из исходного положения h, а v 1 — начальная скорость системы.
Если позиция начинается из покоя, v 1 равно нулю, а время t можно найти, изменив уравнение.
Шаг 5
Подтвердите расчеты. Разрешить запуск системы из состояния покоя с массой m 2 на земле. Измерьте время, за которое масса m 1 достигнет земли.
Шаг 6
Вычислите процентную разницу между вашим теоретическим значением времени и измеренным значением времени.
Дополнительные ресурсы
- Машина Этвуда (артикул № 752019)
- Машина Этвуда Visual Scientifics (артикул № 753174)
- Модуль USB-моста Neulog™ (артикул № 369733)
- Коммуникационный модуль Neulog™ Wi-Fi™ (артикул № 369735)
- Датчик движения Neulog™ (артикул № 369642)
Проблема со шкивами
Ресурс, который поможет вам построить и протестировать рабочие модели систем шкивов, обычно используемых в физических задачах.
Вам также может понравиться
Вам также может понравиться
Этвуд Машина
Артикул № 752019
36,50 долларов США
Быстрый просмотр
Датчик фотоворот NeuLog®
Артикул № 369638
$56,65
Быстрый просмотр
Компания Visual Scientifics Atwood Machine
Артикул № 753174
41,20 доллара США
Быстрый просмотр
Комплект подключения NeuLog® WiFi®
Артикул № 369510
250,65 долларов США
Быстрый просмотр
Датчик движения NeuLog®
Артикул № 369642
100,50 долларов США
Быстрый просмотр
Загрузка…
Машина Этвуда | Национальный музей американской истории
Назад
Следующий
>>
ЗагрузкиЗагрузкиЗагрузкиЗагрузкиЗагрузкиЗагрузки
- Описание
- Джордж Этвуд, преподаватель математики в Тринити-колледже в Кембридже, описал этот тип инструмента в 1784 году, объяснив его использование для проверки законов движения с постоянным ускорением.
 Машина Этвуда вскоре стала обычным учебным оборудованием, подходящим для обучения классической механике.
Машина Этвуда вскоре стала обычным учебным оборудованием, подходящим для обучения классической механике. - Этот пример использовался в Военной академии США. Надпись «Fortin et Herrmann Genre à Paris» относится к Адольфу и Эмилю Фортен-Херрманн, братьям, которые в 1831 году переняли мастерскую своего деда, Николя Фортена, ведущего производителя научных инструментов в Париже.
- Ссылка: Джордж Этвуд, Трактат о прямолинейном движении и вращении тел с описанием оригинальных экспериментов, относящихся к предмету (Кембридж, 1784).
- Даниэль Гранд, «Notice Nécrologique sur Adolphe et Émile Fortin-Herrmann», Mémoires et Compte-rendus de la Société des Ingénieurs Civils de France (1908): 692-700.

- Местоположение
- В настоящее время не отображается
- Имя объекта
- Машина Этвуда
- производитель
- Фортин и Херрманн
- место изготовления
- Франция: Иль-де-Франс, Париж
- Размеры
- общий (объект): 98 1/2 дюйма x 25 3/4 дюйма x 25 3/4 дюйма; 250,19 см x 65,405 см x 65,405 см
- общий (в футляре): 112 дюймов х 35 дюймов х 35 дюймов; 284,48 см х 88,9 см х 88,9 см
- Идентификационный номер
- PH.
 315758
315758 - каталожный номер
- 315758
- регистрационный номер
- 217544
- Кредитная линия
- Военная академия США
- предмет
- Наука и научные инструменты
- Посмотреть больше товаров в
- Медицина и наука: физические науки
- Источник данных
- Национальный музей американской истории
Номинировать этот объект для фотографирования.
 Создать предложение
Создать предложение G — ускорение свободного падения, 9,8 м/с 2 . Символы m 1 и m 2 обозначают массу в килограммах. T – напряжение в ньютонах. Сила измеряется в ньютонах, где 1Н = 1 кг x м/с 2 .
G — ускорение свободного падения, 9,8 м/с 2 . Символы m 1 и m 2 обозначают массу в килограммах. T – напряжение в ньютонах. Сила измеряется в ньютонах, где 1Н = 1 кг x м/с 2 .
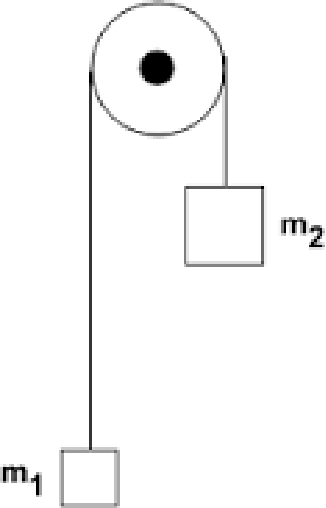 Используйте одно из уравнений кинематики, чтобы найти время, за которое масса m 1 опустится на землю.
Используйте одно из уравнений кинематики, чтобы найти время, за которое масса m 1 опустится на землю.
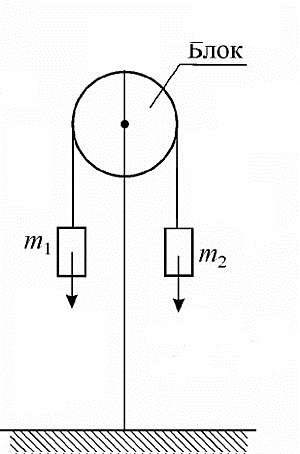 Если позиция начинается из покоя, v 1 равно нулю, а время t можно найти, изменив уравнение.
Если позиция начинается из покоя, v 1 равно нулю, а время t можно найти, изменив уравнение.
 Машина Этвуда вскоре стала обычным учебным оборудованием, подходящим для обучения классической механике.
Машина Этвуда вскоре стала обычным учебным оборудованием, подходящим для обучения классической механике.
 315758
315758