Содержание
PhysBook:Электронный учебник физики — PhysBook
Содержание
-
1 Учебники -
2 Механика-
2.1 Кинематика -
2.2 Динамика -
2.3 Законы сохранения -
2.4 Статика -
2.5 Механические колебания и волны
-
-
3 Термодинамика и МКТ-
3.1 МКТ -
3. 2 Термодинамика
2 Термодинамика
-
-
4 Электродинамика-
4.1 Электростатика -
4.2 Электрический ток -
4.3 Магнетизм -
4.4 Электромагнитные колебания и волны
-
-
5 Оптика. СТО-
5.1 Геометрическая оптика -
5.2 Волновая оптика -
5. 3 Фотометрия
3 Фотометрия
-
5.4 Квантовая оптика -
5.5 Излучение и спектры -
5.6 СТО
-
-
6 Атомная и ядерная-
6.1 Атомная физика. Квантовая теория -
6.2 Ядерная физика
-
-
7 Общие темы -
8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТО
Геометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
Физические основы механики
Рассмотрим теперь плоское движение твердого тела, то есть движение, при котором точки тела описывают траектории, лежащие в параллельных плоскостях. Пример такого движения — вращение колеса автомобиля при его движении по прямой. Можно взять любую точку 0 тела и мысленно провести через нее ось вращения перпендикулярно плоскостям, в которых лежат траектории точек тела. Тогда ось вращения будет двигаться поступательно, оставаясь все время параллельной самой себе.
Пример такого движения — вращение колеса автомобиля при его движении по прямой. Можно взять любую точку 0 тела и мысленно провести через нее ось вращения перпендикулярно плоскостям, в которых лежат траектории точек тела. Тогда ось вращения будет двигаться поступательно, оставаясь все время параллельной самой себе.
Видео 7.2. Плоское движение твердого тела в однородном поле тяжести. Полет плоской картонной фигуры
Соответственно, скорость элементарной массы твердого тела складывается из скорости поступательного движения точки 0 и линейной скорости вращения вокруг связанной с ней (мысленно проведенной) оси:
где — радиус-вектор, определяющий положение элементарной массы по отношению к точке 0.
Кинетическая энергия элементарной массы равна тогда:
Векторное произведение
имеет модуль, равный , где — расстояние массы от оси вращения. Следовательно, третье слагаемое в скобках равно . Второе слагаемое, представляющее собой смешанное произведение векторов, не меняется при циклической перестановке сомножителей:
В результате получим для кинетической энергии элемента твердого тела следующее выражение
Для нахождения кинетической энергии тела просуммируем по всем элементарным массам:
Сумма элементарных масс
есть масса твердого тела. Выражение
Выражение
где — радиус-вектор центра масс тела относительно точки 0.
Наконец,
— есть момент инерции тела относительно оси вращения. Поэтому для кинетической энергии твердого тела можно записать формулу:
Поскольку выбор мысленной оси вращения всецело в нашей власти, мы упростим полученное выражение, взяв в качестве точки 0 центр масс тела. Тогда = 0 и кинетическая энергия тела при плоском движении равна
Здесь — скорость движения центра масс, a — момент инерции относительно оси, проходящей через центр масс и ортогональной плоскости, где лежат траектории точек тела. Таким образом, кинетическая энергия твердого тела при плоском движении слагается из энергии поступательного движения со скоростью, равной скорости центра масс и энергии вращения вокруг оси, проходящей через центр масс тела.
Движение твердого тела определяется действующими на тело внешними силами и моментами этих сил
Индекс в обозначениях для момента внешней силы означает проекцию момента на ось вращения.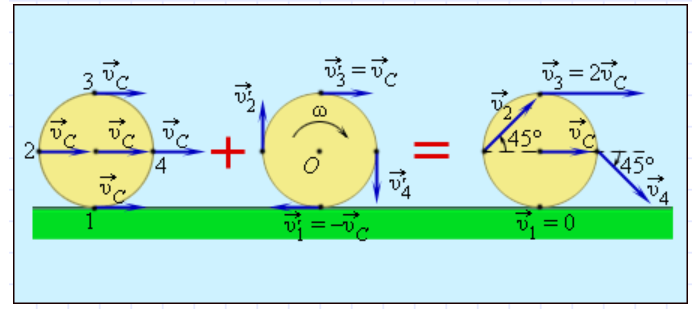
В следующих примерах мы имеем дело с плоским движением.
Видео 7.3. Зависимость поведения цилиндров на наклонной плоскости от характера распределение массы по их объему
Пример 1. Круглое однородное тело (обруч, цилиндр, шар) радиусом и массой скатывается без скольжения по наклонной плоскости под углом к горизонту с высоты (рис. 7.12). Начальная скорость тела равна нулю. Найдем скорость центра масс каждого тела в конце спуска.
Рис. 7.12. Скатывание тела с наклонной плоскости
Рассмотрение данной задачи можно вести двумя способами.
1-й способ. По условию тело катится без проскальзывания. Это условие используется у нас дважды. Сила трения между телом и плоскостью действует в точке соприкосновения и в отсутствие скольжения не превышает своего максимального значения:
где — коэффициент трения скольжения.
Оси координат удобно направить следующим образом: ось х — вдоль движения, ось у — перпендикулярно наклонной плоскости. Тело движется под действием трех сил: силы тяжести , силы трения и силы нормального давления , так что уравнение поступательного движения центра инерции тела имеет вид:
Тело движется под действием трех сил: силы тяжести , силы трения и силы нормального давления , так что уравнение поступательного движения центра инерции тела имеет вид:
Вдоль оси у тело не движется. Проецируя уравнение движения центра масс на ось у, получаем для силы нормального давления соотношение:
Проекция уравнения движения на ось х дает:
Так как линейная скорость точек соприкосновения цилиндра с наклонной плоскостью равна нулю (опять используем условие отсутствия проскальзывания), то скорость (ускорение) поступательного движения связаны с угловой скоростью (угловым ускорением) тела обычными соотношениями:
Кроме поступательного движения, тело еще и вращается. Вращение удобно описывать относительно оси z, проходящей через центр масс цилиндра.
Выбор этот обусловлен тем, что линии действия силы тяжести и силы нормального давления плоскости проходят через ось вращения и, следовательно, моменты этих сил равны нулю. Таким образом, цилиндр вращается только под действием силы трения, и уравнение вращательного движения имеет вид:
Таким образом, цилиндр вращается только под действием силы трения, и уравнение вращательного движения имеет вид:
Таким образом, получается система 4-х уравнений, описывающих поступательное и вращательное движение с дополнительным неравенством, выражающим закон трения. Решая систему уравнений, находим:
Чем больше момент инерции относительно оси, проходящей через центр масс, тем меньше ускорение тела. Мы уже получили ответ на один из вопросов задачи: шар будет двигаться быстрее цилиндра, а цилиндр — быстрее обруча. Подставляя решение для силы трения в неравенство, выражающее закон трения, находим условие, при котором будет отсутствовать проскальзывание:
Смысл этого условия прост: наклон не должен быть слишком крут.
Итак, центр масс тела движется вдоль плоскости с постоянным ускорением a, так что зависимость пройденного пути и скорости от времени имеет вид:
Отсюда следует связь скорости и пройденного пути:
К концу спуска тело проходит путь
так что его скорость достигает величины
Подставляя сюда моменты инерции обруча (), цилиндра () и шара (), находим соответственно:
2-й способ. Используем закон сохранения полной энергии. В конце спуска тело приобретает кинетическую энергию
Используем закон сохранения полной энергии. В конце спуска тело приобретает кинетическую энергию
Эта кинетическая энергия приобретена за счет потенциальной энергии . Отсюда следует найдено выше выражение для скорости тела в конце спуска. Такой способ намного короче, но он не позволяет узнать детали процесса: действующие на тело силы и т.п.
В рассмотренном выше примере мы считали примере мы имели дело со случаем, когда проскальзывание отсутствовало. Это позволило утверждать простую связь () между угловой и линейной скоростями тела и его радиусом. Сила трения покоя находилась при этом в результате решения уравнений движения. В случае, когда тело движется с проскальзыванием, заранее известной связи между линейной и угловой скоростями нет. Зато мы заранее знаем силу трения: раз точка соприкосновения тела с поверхностью скользит по поверхности, сила трения есть сила трения скольжения,модуль которой связан с силой нормального давления законом Амонтона — Кулона.
Силы трения, как уже говорилось, направлены так, чтобы препятствовать относительному проскальзыванию соприкасающихся тел. Часто путают это возможное проскальзывание с осуществляемым поступательным движением. Необходимо четко понимать, что не редки случаи, когда сила трения не тормозит, но ускоряет тело, то есть направлена по его движению. Самый известный пример — трогание автомобиля с места. Колеса начинают вращаться и проскальзывают по земле назад. Соответственно, сила трения направлена вперед, и именно она заставляет автомобиль трогаться. Чтобы ближе познакомиться с подобными случаями, рассмотрим пример.
Часто путают это возможное проскальзывание с осуществляемым поступательным движением. Необходимо четко понимать, что не редки случаи, когда сила трения не тормозит, но ускоряет тело, то есть направлена по его движению. Самый известный пример — трогание автомобиля с места. Колеса начинают вращаться и проскальзывают по земле назад. Соответственно, сила трения направлена вперед, и именно она заставляет автомобиль трогаться. Чтобы ближе познакомиться с подобными случаями, рассмотрим пример.
Пример 2. Цирковой артист бросает на арену обруч массой и радиусом , который начинает катиться в горизонтальном направлении со скоростью (рис. 7.13). При этом обручу придано обратное вращение с угловой скоростью . Найдем, при какой угловой скорости обруч после остановки покатится назад к артисту, а также конечную скорость поступательного движения обруча.
Рис. 7.13. Движение обруча с обратным вращением
При обратном вращении обруча точка его касания с ареной движется вперед как из-за вращения, так и из-за поступательного движения обруча. Поэтому неизбежно существует проскальзывание и, значит, сила трения достигает своего максимального значения. Она тормозит как поступательное движение, так и вращение обруча. Может случиться так, что поступательное движение обруча будет остановлено в тот момент, когда он еще сохраняет обратное вращение. Далее сила трения начнет ускорять обруч по направлению к артисту. Ускорение это прекратится, когда исчезнет тенденция к проскальзыванию, после чего обруч покатится назад равномерно с некоторой установившейся скоростью . Может, однако, случиться и так, что раньше будет остановлено обратное вращение, и тогда обруч сохранит поступательное движение вперед, изменив направление вращения на прямое. Чтобы различить эти два случая, качественных рассуждений недостаточно, и мы обратимся к формулам.
Поэтому неизбежно существует проскальзывание и, значит, сила трения достигает своего максимального значения. Она тормозит как поступательное движение, так и вращение обруча. Может случиться так, что поступательное движение обруча будет остановлено в тот момент, когда он еще сохраняет обратное вращение. Далее сила трения начнет ускорять обруч по направлению к артисту. Ускорение это прекратится, когда исчезнет тенденция к проскальзыванию, после чего обруч покатится назад равномерно с некоторой установившейся скоростью . Может, однако, случиться и так, что раньше будет остановлено обратное вращение, и тогда обруч сохранит поступательное движение вперед, изменив направление вращения на прямое. Чтобы различить эти два случая, качественных рассуждений недостаточно, и мы обратимся к формулам.
Направим ось ОХ направо (в направлении красной стрелки на рис. 7.13), ось вращения ОZ направим на нас (см. следующий пример, там эту ось удобнее направить от нас, то есть за чертеж), то есть в направлении «обратного» вращения, ось OY направим как обычно, вверх.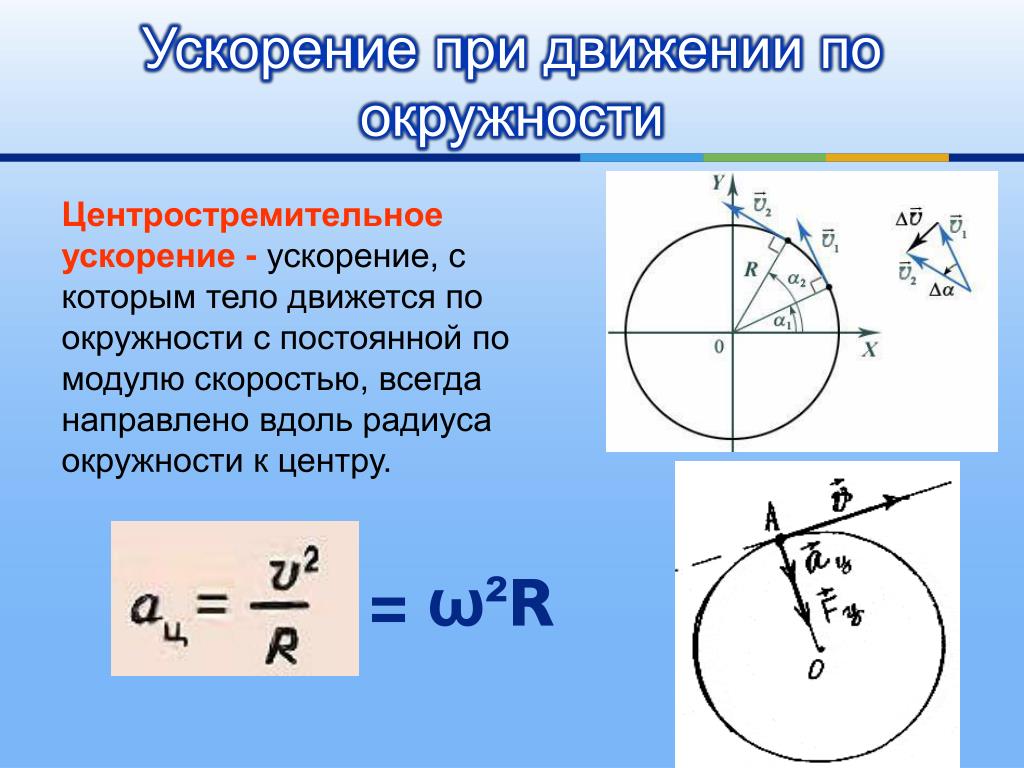 Плоское движение обруча представим как суперпозицию его поступательного движения вместе с центром масс (геометрическим центром, поскольку обруч предполагается однородным). Спроектируем линейные и угловые скорости на соответствующие оси. Тогда, до тех пор, пока сила трения есть сила трения скольжения и направлена она налево, уравнения движения имеют вид
Плоское движение обруча представим как суперпозицию его поступательного движения вместе с центром масс (геометрическим центром, поскольку обруч предполагается однородным). Спроектируем линейные и угловые скорости на соответствующие оси. Тогда, до тех пор, пока сила трения есть сила трения скольжения и направлена она налево, уравнения движения имеют вид
(7.3.1)
(7.3.2)
Уравнение (7.3.1) описывает движение центра масс обруча, а уравнение (7.3.2) его вращение вокруг оси проходящей через центр масс в той системе отсчета, в которой она покоится (системе центра масс). В (7.3.2) учтено, что момент инерции однородного обруча относительно его оси симметрии равен . После элементарного интегрирования получаем
(7.3.3)
(7.3.4)
Поступательное движение прекратится, то есть станет равным нулю, в момент времени
(7.3.5)
Вращение прекратится, то есть станет равным нулю,в момент времени
(7.3.6)
Их отношение
(7. 3.7)
3.7)
может быть любым ввиду независимости начальных скоростей поступательного и вращательного движений.
Для дальнейшего анализа введем в рассмотрение скорость нижней точки обруча — той его точки, которая касается поверхности арены. Отметим уже здесь, что условием исчезновения проскальзывания является обращение в ноль скорости именно этой точки, потому что скорость соответствующей точки на поверхности арены (той, которой касается обруч) очевидным образом в нашей системе отсчета, где арена неподвижна, равна нулю. Отсутствие проскальзывания это и есть неподвижность этих двух точек относительно друг друга. При выбранном направлении осей OZ и OX, имеем
(7.3.8)
Если , то первым прекратится поступательное движение обруча. В момент времени скорости (7.3.3) и (7.3.8) будут иметь значения
Нижняя точка обруча, за счет продолжающегося вращения, будет по-прежнему скользить относительно арены направо (направо на рисунке 7.13), сила трения скольжения сохранит свою величину и направление налево. Соответственно, центр обруча начнет ускорятся налево, то есть станет меньше нуля и начнет расти по модулю, вращение против часовой стрелки (на рисунке 7.13) будет продолжать замедлятся. Другими словами, при обруч в момент времени (7.3.5) начинает возвращаться к бросившему его артисту.
Соответственно, центр обруча начнет ускорятся налево, то есть станет меньше нуля и начнет расти по модулю, вращение против часовой стрелки (на рисунке 7.13) будет продолжать замедлятся. Другими словами, при обруч в момент времени (7.3.5) начинает возвращаться к бросившему его артисту.
Как следует из (7.3.8), в момент времени
(7.3.9)
скорость нижней точки обруча из (7.3.8) обращается в ноль, проскальзывание прекращается, сила трения скольжения скачком сменяется равной нулю силой трения покоя (силой трения качения пренебрегаем) и обруч начинает катится к артисту с постоянной скоростью движения центра масс
(7.3.10)
вращаясь против часовой стрелки с постоянной угловой скоростью
(7.3.11)
Если , то первым, в момент времени (7.3.6), прекратится вращение обруча. В момент времени скорость (7.3.8) нижней точки обруча будет равна скорости его центра и положительна:
(7.3.12)
Скольжение остается, сила трения скольжения сохраняет свою величину и направление налево, но обруч под действием этой силы трения скольжения начинает вращаться по часовой стрелке (напоминаем: налево, направо, по или против часовой стрелки — на рисунке 10).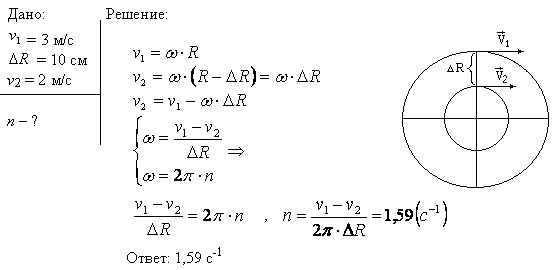 В результате этого скорость центра масс (центра обруча) будет уменьшаться, скорость вращения увеличиваться, в момент времени
В результате этого скорость центра масс (центра обруча) будет уменьшаться, скорость вращения увеличиваться, в момент времени
(7.3.13)
проскальзывание обруча прекратится и обруч начнет равномерно удаляться от артиста со скоростью центра (7.3.10) и угловой скоростью вращения (7.3.11). Напомним, что в этом случае , так что а
Таким образом, ответ на вопрос: «Вернется обруч или укатится?» определяется начальными условиями, а конкретнее величиной параметра , который имеет простой физический смысл: это отношение модуля
скорости любой точки обруча за счет его поступательного движения вместе с центром масс к модулю скорости той же точки за счет вращения обруча вокруг оси, проходящей через его центр масс, в начальный момент времени.
Пример 3. Описать движение обруча (см. предыдущий пример), если ему придано прямое вращение (рис. 7.14). Поскольку обруч вращается теперь на рис. 7.14 по часовой стрелке, направим ось вращения OZ от нас, то есть за чертеж — в отличие от предыдущего случая.
Рис. 7.14. Движение обруча с прямым вращением: 1 – ; 2 –
Начальная скорость нижней точки обруча складывается из скорости поступательного движения и линейной скорости за счет вращения, направленной в противоположную сторону. В связи с этим надо различать два случая.
1 случай или . Тогда начальная скорость нижней точки обода положительна, то есть, направлена в ту же сторону, что и скорость . Значит, сила трения f направлена в противоположную сторону, как показано на рис. 11–1. В связи с изменением положительного направления оси вращения необходимо лишь изменить знак перед вторым слагаемым в уравнении (7.3.4). Решение уравнений движения в рассматриваемом случае имеют вид
(7.3.14)
(7.3.15)
При новом выборе направления оси вращения скорость нижней точки обруча записывается в виде
(7.3.16)
Момент исчезновения проскальзывания определится из того же соотношения равенства нулю скорости нижней точки обруча или равенства по модулю противоположно направленных скоростей этой точки за счет поступательного движения вместе с центром масс и вращательного движение вокруг оси, проходящей через центр масс:
откуда находим:
Скорость поступательного движения обруча в этот момент становится равной
и остается потом неизменной. Эта скорость меньше начальной скорости поступательного движения обруча.
Эта скорость меньше начальной скорости поступательного движения обруча.
2 случай или . В этом случае скорость нижней точки обода отрицательна, направлена против скорости . Значит, сила трения направлена по (см. рис.11-2).
Соответственно, в уравнениях движения и их решениях (7.3.14) и (7.3.15) надо изменить знаки на противоположные перед вторыми слагаемыми, содержащими изменившую направление силу трения, получаем:
(7.3.17)
(7.3.18)
Соответственно, выражение для скорости нижней точки обруча приобретает вид:
(7.3.19)
Момент прекращения проскальзывания определяется аналогично и оказывается равным:
а для скорости установившегося движения получается вновь выражение
но в данном случае она будет больше () начальной скорости поступательного движения.
Объединяя оба случая в один, записываем окончательный результат:
Дополнительная информация
http://www. plib.ru/library/book/14978.html Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г. — стр. 256 (§ 48, задача 9): рассмотрено движение маятника Максвелла, включая силу натяжения нитей подвеса в нижней точке.
plib.ru/library/book/14978.html Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г. — стр. 256 (§ 48, задача 9): рассмотрено движение маятника Максвелла, включая силу натяжения нитей подвеса в нижней точке.
http://kvant.mirror1.mccme.ru/pdf/1997/04/kv0497khorozov.pdf — журнал «Квант» — решение задачи об отскоке вращающегося мяча от плоской стенки (С. Хорозов).
http://kvant.mirror1.mccme.ru/pdf/1998/04/kv0498chernoutsan.pdf — журнал «Квант» — применение законов динамики твердого тела в задаче о падении вертикальной палочки на горизонтальный стол (А. Черноуцан).
http://kvant.mirror1.mccme.ru/pdf/1999/02/kv0299chernoutsan.pdf — журнал «Квант» — продолжение задачи о падении вертикальной палочки на горизонтальный стол (А. Черноуцан).
Что такое линейная скорость (Видео)
Стенограмма
Привет, добро пожаловать в это видео о линейной скорости!
Представьте, что вы бежите вперед и прыгаете на вращающуюся карусель. Сначала вы бежите по прямой, но когда приземляетесь, ваше движение меняется, и вы начинаете вращаться. Как ваша скорость бега связана со скоростью вращения? Давай выясним!
Как ваша скорость бега связана со скоростью вращения? Давай выясним!
Во-первых, напомним, что скорость — это расстояние, пройденное за определенный промежуток времени. В автомобилях есть спидометр, который сообщает нам скорость автомобиля в милях в час — мили в качестве единиц расстояния и часы в качестве единиц времени. Линейная скорость говорит нам, как быстро движется точка на вращающемся объекте. Расстояние, которое проходит точка, зависит от того, насколько далеко она находится от центра вращения. Точка, находящаяся дальше от центра вращения, перемещается дальше, чем точка, расположенная ближе к центру вращения. Время – это время, за которое объект совершает один оборот.
Мы вычисляем линейную скорость точки, используя несколько различных методов. Во-первых, нам нужно найти расстояние, пройденное точкой, а для этого нам нужно знать, как далеко точка находится от центра вращения; это радиус круга, который объект создает при вращении. Назовем это р. Далее нам нужно измерить, насколько далеко повернулась точка. Это угол , через который прошел объект, θ, который измеряется в радианах или градусах. Получив эти два измерения, мы вычисляем длину дуги, то есть расстояние, пройденное точкой. Мы называем это расстояние s и используем уравнение s=rθ. Теперь, когда у нас есть пройденное расстояние, мы измеряем время, необходимое для прохождения этого расстояния, t, и находим линейную скорость: v = s/t = rθ/t.
Это угол , через который прошел объект, θ, который измеряется в радианах или градусах. Получив эти два измерения, мы вычисляем длину дуги, то есть расстояние, пройденное точкой. Мы называем это расстояние s и используем уравнение s=rθ. Теперь, когда у нас есть пройденное расстояние, мы измеряем время, необходимое для прохождения этого расстояния, t, и находим линейную скорость: v = s/t = rθ/t.
Иногда мы знаем, как быстро что-то вращается, и мы хотим рассчитать линейную скорость. Обычно мы знаем, сколько оборотов в минуту делает объект, поэтому давайте соединим RPM и линейную скорость.
Напомним, что угол можно измерять двумя разными единицами измерения: радианами или градусами. Полный оборот составляет 2π радиан или 360 градусов. При преобразовании между скоростью вращения и линейной скоростью единицы, которые мы используем, зависят от окончательного ответа, который мы хотим. Сначала воспользуемся радианами.
Предположим, у нас есть колесо, вращающееся со скоростью ω об/мин с радиус р метров. Какова линейная скорость в метрах в секунду точки на самом внешнем краю шины?
Какова линейная скорость в метрах в секунду точки на самом внешнем краю шины?
Мы можем использовать простой модульный анализ, чтобы найти ответ! Во-первых, мы знаем, что наше колесо вращается на 2π радиан за один оборот. Но как мы соотносим радианы с длиной в метрах? Представьте, что наше колесо обмотано веревкой. Эта струна делает один оборот вокруг нашего колеса. Он «измеряет» 2π радиан. Теперь давайте возьмем этот кусок веревки, разложим его и измерим линейкой его длину. Найдем длину 2πr метров. Таким образом, за каждый оборот наше колесо проходит 2πr метров. Чтобы перевести минуты в секунды, вспомните, что в одной минуте 60 секунд. Итак, мы видим,
В общем случае используется формула v = 2πrω, где r — расстояние от точки вращения до центра вращения, а ω — скорость вращения объекта. Давайте рассмотрим пример задачи:
Земля совершает один оборот вокруг Солнца за один год. Это примерно 93 миллиона миль от Солнца. Какова линейная скорость Земли в милях в час? Воспользуемся формулой v=2r с некоторыми изменениями единиц. У нас есть ω в единицах оборотов в год. Мы можем следовать модульному анализу, чтобы найти линейную скорость. В одном году 365,25 дня (каждые четыре года бывает високосный год, что эквивалентно добавлению к каждому году одной четверти дня), а в одном дне 24 часа. Тогда один оборот равен 2πr, где r равно 9.3 миллиона миль. Итак, мы видим, что Земля движется со скоростью 66 ТЫСЯЧ миль в час!
У нас есть ω в единицах оборотов в год. Мы можем следовать модульному анализу, чтобы найти линейную скорость. В одном году 365,25 дня (каждые четыре года бывает високосный год, что эквивалентно добавлению к каждому году одной четверти дня), а в одном дне 24 часа. Тогда один оборот равен 2πr, где r равно 9.3 миллиона миль. Итак, мы видим, что Земля движется со скоростью 66 ТЫСЯЧ миль в час!
Но что, если мы используем градусы для измерения угла, а не радианы? Наше колесо с радиусом r теперь вращается со скоростью 60 градусов в минуту, и мы хотели бы знать линейную скорость в футах в секунду. Самый простой способ — добавить еще одно преобразование единиц измерения: преобразовать градусы в обороты! Затем вы можете использовать те же шаги, чтобы найти линейную скорость!
В общем случае используется формула v = 2πrω/180, где r — расстояние от вращающегося объекта до центра вращения, а ω — скорость вращения объекта в градусах в секунду.
Давайте посмотрим на другой пример:
Колесо обозрения Centennial на морском пирсе Чикаго поднимает пассажиров почти на 200 футов в высоту. Одна поездка длится примерно 15 минут, и вы можете объехать 3 раза. Какова ваша средняя линейная скорость в футах в секунду?
Одна поездка длится примерно 15 минут, и вы можете объехать 3 раза. Какова ваша средняя линейная скорость в футах в секунду?
Во-первых, нам дан диаметр колеса обозрения, а не радиус. Напомним, что диаметр круга в 2 раза больше радиуса, поэтому r = 100 футов. Далее нам нужно выяснить, как быстро мы вращаемся. Вращаемся 3 раза за 15 минут, что равно 1 вращению за 5 минут. Теперь мы можем использовать
v = 2πrω, чтобы найти нашу линейную скорость примерно равной 2 футам в секунду.
Спасибо за просмотр и удачной учебы!
- «Круговое движение: линейная и угловая скорость ‹ OpenCurriculum». 2020
- «Формула линейной скорости (вращающийся объект)». нд
- Шарп, Тим. 2017. «Как далеко Земля от Солнца?» Space.com.
спросил
Изменено
4 года, 1 месяц назадПросмотрено
46 тысяч раз$\begingroup$
Когда колесо катится, а не скользит, и его ось движется со скоростью $\vec{v}$, тогда точка на вершине его окружности будет двигаться со скоростью $2\vec{v}$, как показано ниже.

Я действительно этого не понимаю. Я хорошо знаком с геометрией круга, но не понимаю, как она применяется в данном случае. Также:
- Почему отношение скоростей не зависит от радиуса колеса?
- Когда это отношение действительно? Учитывается ли трение или это не имеет значения? Если не важно, то почему?
- Следствием всего этого является то, что точка на дне не имеет скорости. Почему? Это не имеет смысла для меня.
Для меня это очень запутанная тема. Вот очень хорошая страница, полная картинок и анимаций о физике колеса, но я все еще не понимаю.
- кинематика
- кинематика вращения
$\endgroup$
1
$\begingroup$
Я отвечу на ваши вопросы в обратном порядке:
3. Точка контакта неподвижна, потому что колесо не проскальзывает. Это происходит, когда сила трения покоя способна противостоять силе колеса о землю. Это то, что вам нужно для управляемого транспорта.
 Если колесо начинает проскальзывать (из-за низкого трения), это занос, и вы больше не можете управлять или тормозить. Если хотите, представьте, что ваша машина застряла в грязи. Вы крутите колесо и разбрасываете грязь повсюду, но никуда не денетесь — недостаточно трения. Если это не поможет, попробуйте взять колесо, отметить на нем точку и медленно катить его, внимательно наблюдая за точкой контакта.
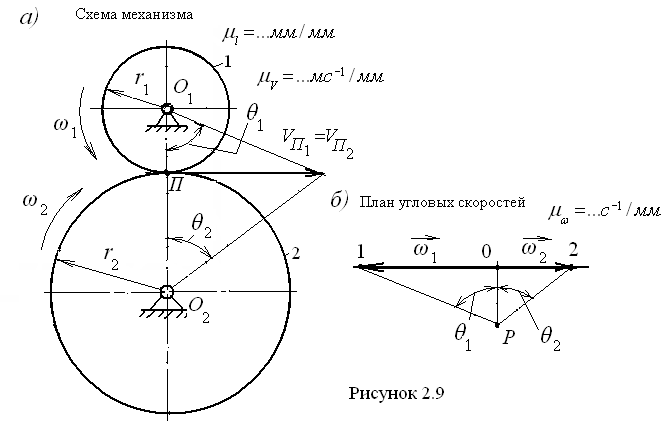
Если колесо начинает проскальзывать (из-за низкого трения), это занос, и вы больше не можете управлять или тормозить. Если хотите, представьте, что ваша машина застряла в грязи. Вы крутите колесо и разбрасываете грязь повсюду, но никуда не денетесь — недостаточно трения. Если это не поможет, попробуйте взять колесо, отметить на нем точку и медленно катить его, внимательно наблюдая за точкой контакта.2. Вам необходимо достаточное статическое трение, чтобы обеспечить условие прилипания. Соотношение между скоростью вверху, в центре и внизу колеса является геометрическим и не зависит от трения как такового. Если колесо автомобиля вращается с угловой частотой $\omega$, имеет радиус $R$ и скорость на оси $v$, то скорость колеса вверху и внизу равна $$ v_{top} = v + \ omega R, v_{bottom} = v — \omega R $$
1. Если выполняется условие прилипания, то $v_{bottom}=0$, поэтому $ v = \omega R $. Использование этого в верхнем уравнении дает $ v_{top} = v + v = 2v $, не зависящее от $R$.
 Это связано с тем, что и $v$, и $v_{top}$ увеличиваются в той же пропорции, что и $R$.
Это связано с тем, что и $v$, и $v_{top}$ увеличиваются в той же пропорции, что и $R$.(Кроме того: есть ли способ заставить уценку делать обратные списки?)
$\endgroup$
6
$\begingroup$
Наденьте очки «мгновенного действия».
т.е. подумайте о том, что происходит в очень-очень короткий момент времени.
Либо так, либо колесо крутится очень, очень, очень медленно.
Либо так, либо предположим, что он вообще не вращается, если только вы не переместите его верхнюю часть вперед на 1 миллиметр.Теперь предположим, что это вовсе не колесо.
Предположим, это просто палка или стержень, начиная снизу, где он не скользит по дороге, и заканчивая тем, где вы его немного передвинули.
Или предположим, что это колесо, но вы нарисовали на нем линию снизу вверх, так что эта линия похожа на палку.Хорошо, вы сдвинули верхнюю часть на 1 миллиметр.
Как далеко сдвинулось дно? (ноль — нет проскальзывания)
На какое расстояние переместилась ось, учитывая, что она наполовину поднята?Бери оттуда.
 ..
..$\endgroup$
1
$\begingroup$
Колесо катится без средств проскальзывания, любая точка на окружности колеса будет иметь как вращательное, так и поступательное движение. Благодаря переносу, если скорость транспортного средства равна v м/с, то все точки колеса будут иметь линейную скорость v м/с в прямом направлении. Тогда за счет вращательного движения каждая точка будет иметь линейную скорость v = rω, где ω — угловая скорость. Для самой верхней точки в конкретный момент линейная скорость будет направлена вперед по горизонтали. Таким образом, в любой момент самая верхняя точка колеса будет иметь две линейные скорости одинаковой величины $v_\mathrm{total} = v+v = 2v$.
Проскальзывание означает, что все точки колеса будут двигаться с одинаковой скоростью. Таким образом, нет вращательного движения и, следовательно, нет дополнительной линейной составляющей скорости. Итак, $v_\mathrm{total} = v+0 = v$. Следовательно, приведенное выше уравнение справедливо только тогда, когда колесо катится без проскальзывания.
 (Пробуксовка или занос колес транспортного средства происходит, когда тормоза полностью задействованы, а транспортное средство все еще движется, но колеса не вращаются).
(Пробуксовка или занос колес транспортного средства происходит, когда тормоза полностью задействованы, а транспортное средство все еще движется, но колеса не вращаются).Кроме того, это условие действительно только для конкретной точки в конкретный момент времени. В следующее мгновение рассматриваемая нами точка будет иметь скорость, а другая точка, расположенная совсем рядом с предыдущей, будет иметь нулевую скорость, потому что иначе, если точка, касающаяся земли, имеет скорость, это означает, что колесо скользит, а не катится.
$\endgroup$
$\begingroup$
Начнем со свободно движущегося тела. Представьте твердый стержень радиуса $r$, прикрепленный перпендикулярно к оси (как стержни велосипеда, к которым прикреплены педали). Предположим, что ось ориентирована горизонтально относительно горизонтальной плоскости, поэтому стержень может двигаться в плоскости, перпендикулярной этой горизонтальной плоскости.
Теперь пусть стержень вращается, и представим, что внешняя часть стержня движется со скоростью $\vec v$ (которая, очевидно, имеет разное направление в каждой точке окружности, описываемой стержнем).
 В этот момент вся конструкция неподвижна относительно горизонтальной плоскости.
В этот момент вся конструкция неподвижна относительно горизонтальной плоскости.Затем мы позволим стержню и оси (какими бы то ни было средствами) двигаться со скоростью $\vec v$ в направлении скорости, с которой стержень имеет наивысшую точку.
Понятно, что верхняя часть стержня теперь имеет скорость $2\vec v$, а нижняя часть имеет скорость (скорость) $0$ (для колеса это означает, что существует сила трения, противодействующая заданной скорости $\ vec v$ на всей структуре).
Таким образом, скорость внешней части стержня (колеса) варьируется от $0$ (когда она достигает самой низкой точки) до $2v$ (когда она достигает самой высокой точки). Таким образом, ни одна точка на внешнем стержне никогда не движется назад.
Я думаю, что ответ на ваш первый вопрос связан с бесконечно малым $2ds$, изображаемым как конечное расстояние (а $2ds$ — это на окружности), что может навести на мысль, что скорости колесо действительно зависит от радиуса.

 2 Термодинамика
2 Термодинамика
 3 Фотометрия
3 Фотометрия

 Если колесо начинает проскальзывать (из-за низкого трения), это занос, и вы больше не можете управлять или тормозить. Если хотите, представьте, что ваша машина застряла в грязи. Вы крутите колесо и разбрасываете грязь повсюду, но никуда не денетесь — недостаточно трения. Если это не поможет, попробуйте взять колесо, отметить на нем точку и медленно катить его, внимательно наблюдая за точкой контакта.
Если колесо начинает проскальзывать (из-за низкого трения), это занос, и вы больше не можете управлять или тормозить. Если хотите, представьте, что ваша машина застряла в грязи. Вы крутите колесо и разбрасываете грязь повсюду, но никуда не денетесь — недостаточно трения. Если это не поможет, попробуйте взять колесо, отметить на нем точку и медленно катить его, внимательно наблюдая за точкой контакта. Это связано с тем, что и $v$, и $v_{top}$ увеличиваются в той же пропорции, что и $R$.
Это связано с тем, что и $v$, и $v_{top}$ увеличиваются в той же пропорции, что и $R$. ..
.. (Пробуксовка или занос колес транспортного средства происходит, когда тормоза полностью задействованы, а транспортное средство все еще движется, но колеса не вращаются).
(Пробуксовка или занос колес транспортного средства происходит, когда тормоза полностью задействованы, а транспортное средство все еще движется, но колеса не вращаются).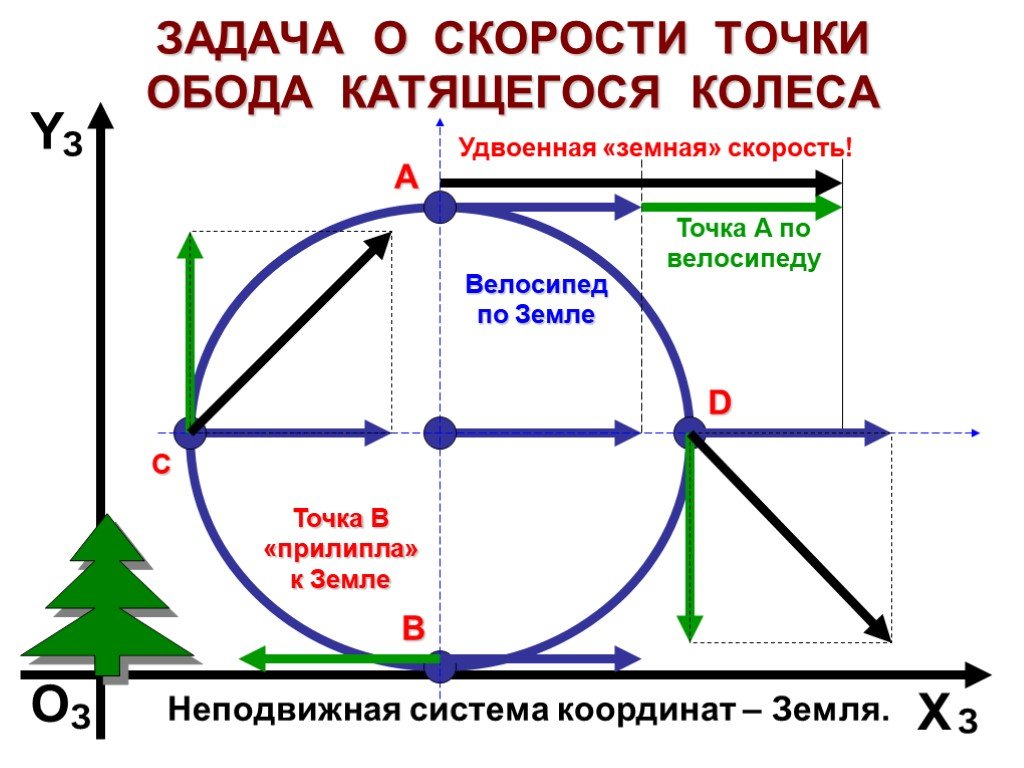 В этот момент вся конструкция неподвижна относительно горизонтальной плоскости.
В этот момент вся конструкция неподвижна относительно горизонтальной плоскости.