Содержание
КПД теплового двигателя — Технарь
Всякий тепловой двигатель превращает в механическую энергию только часть той энергии, которая выделяется топливом, так как газ или пар, совершив работу, выходит из двигателя, обладая еще энергией.
Для оценки теплового двигателя очень важно знать, какую часть энергии, выделяемой топливом, он превращает в полезную работу. Чем эта часть больше, тем двигатель экономичнее.
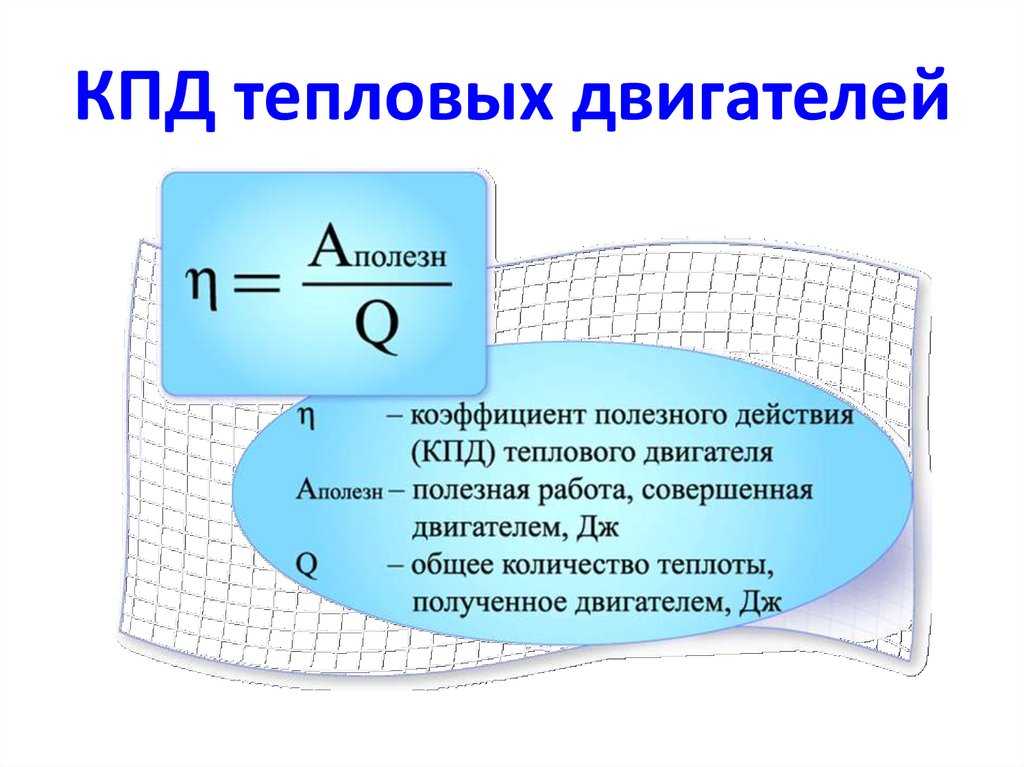
Для характеристики экономичности различных двигателей введено понятие коэффициента полезного действия двигателя (КПД).
Отношение той части энергии, которая пошла на совершение полезной работы двигателя, но всей энергии, выделившейся при полном сгорании топлива, называют коэффициентом полезного действия (КПД) теплового двигателя.
Например, если двигатель из всей энергии, выделившейся при полном сгорании топлива, расходует на совершение полезной работы только одну четвертую часть, то говорят, что коэффициент полезного действия двигателя равен 1/4 или 25%, так как КПД обычно выражают в процентах.
КПД двигателя всегда меньше единицы, т. е. меньше 100%. Это следует из закона сохранения энергии. Например, КПД двигателей внутреннего сгорания 20—40%, паровых турбин — около 30%.
Увеличение числа автомашин, особенно в городах, приводит к сильному загрязнению атмосферы выхлопными газами двигателей внутреннего сгорания. Эти газы вредны для живых организмов, кроме того, они вызывают порчу ценных архитектурных сооружений.
Борьба с загрязнением атмосферы в настоящее время является серьезной государственной задачей.
Наиболее эффективный способ борьбы — замена двигателей внутреннего сгорания электрическими двигателями. Необходимые для этих машин источники тока должны обладать большими запасами энергии, над созданием таких источников тока работают ученые.
Чтобы, существующие автомашины меньше загрязняли воздух, их двигатели должны быть всегда исправны и работать на том виде топлива, на которое они изготовлены. За этим всем нам следует тщательно следить.
Вопросы.
- Почему в тепловых двигателях только часть энергии топлива превращается в механическую энергию?
- Что называют КПД теплового двигателя?
- Может ли двигатель иметь КПД, равный 100%? Почему?
- Назовите коэффициенты полезного действия современных тепловых двигателей.
Задание.
Приготовьте доклады на темы:
- История изобретения паровых машин.
- История изобретения турбин.
- Первые паровозы Стефенсона и Черепановых.
- Достижения советской науки и техники в строительстве паровых турбин.
- Использование энергии Солнца на Земле (прочтите об этом параграф в конце учебника).
Метки: внутренняя энергиядвигательдвигатель внутреннего сгораниякоэффициент полезного действияКПДмеханическая энергияпарпаровая машинапаровозыработаработа двигателятеплотепловая энергияТепловой двигательтопливотурбинаэлектрический двигательэнергия
Правда и мифы о КПД теплового насоса | Полезное
Преимуществом альтернативных источников энергии является их доступность и дешевизна.
Тепловые насосы (тн) используют преобразованную энергию воздуха, воды или грунта, которые являются бесплатными в отличие от газа или угля. Но следует учитывать, что при установке тепловых насосов большие капитальные вложения, которые требуют времени, чтобы окупиться.
Расчет КПД теплового насоса может привести к абсурдным значениям, когда он будет больше 100%. Стандартная формула вычисления КПД некорректна и ошибкой обычно является неучтенный источник энергии (воздух, вода или грунт). У тепловых насосов 2 источника энергии — это электричество и внешний источник тепла (энергия воды, грунта, воздуха), а обычные формулы учитывают только электроэнергию, поэтому получаются значения больше 100%.
Некорректный расчет КПД тн:
Исходные данные:
- потребление электричества 2 КВт;
- отдает в систему 5 Квт;
- из внешнего источника 6 Квт.
Расчет:
Pпотр./Pсети = 5/2 = 2,5
Такой расчет неправильный, так как здесь нет данных второго источника энергии.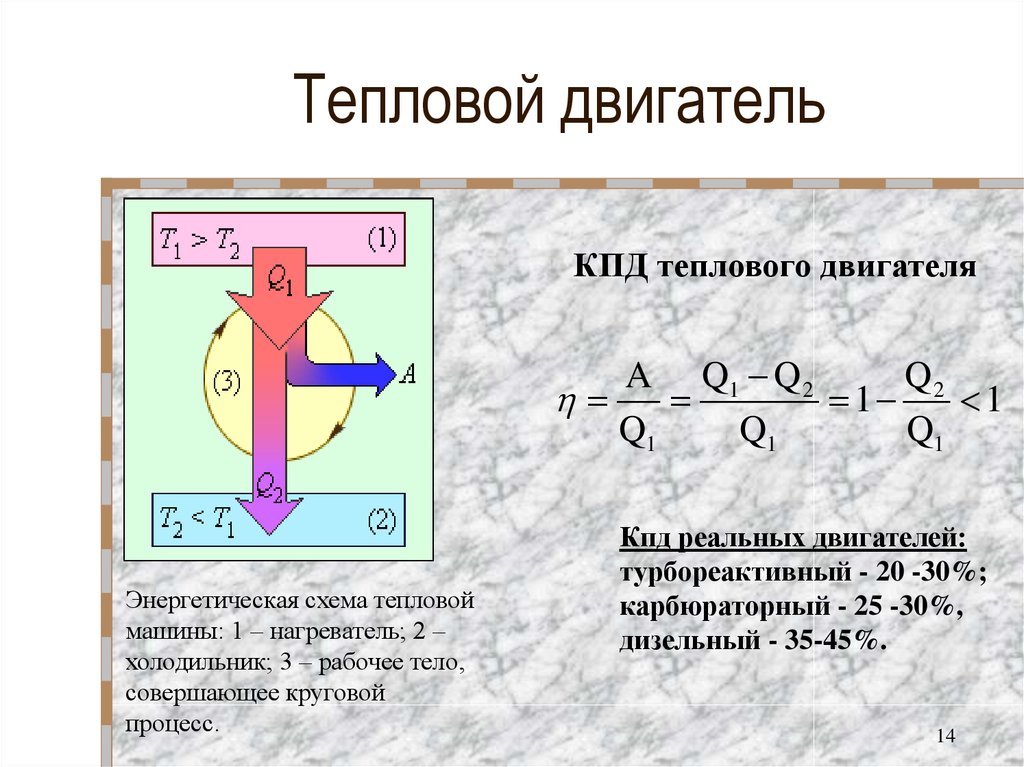
Корректный расчет КПД тн:
Pпотр. /(Pсети + Pист.) = 5 /(2 + 6) = 0,63
Узнать количество низкопотенциальной энергии довольно затруднительно, что и приводит к ошибке.
Чтобы избежать неправильных расчётов были введены специальные коэффициенты:
- COP — определяет во сколько раз тепловая энергия, которую получил потребитель, превышает количество работы необходимой для переноса тепла от низкопотенциального источника;
- степень термодинамического совершенства — оценивает насколько действительный тепловой цикл насоса приближен к идеальному.
В поисках теплонасоса можно наткнуться на рекламное объявление, содержащее неправильную характеристику устройства. Продавцов, распространяющих подобные данные, следует остерегаться. Ведь заявлять, что КПД теплового насоса составляет 300 – 1000% – не только безграмотно, но и некорректно по отношению к покупателям.
Сравнение КПД тепловых насосов: вода, грунт, воздух
Поскольку реально оценить количество энергии, извлекаемой из альтернативного источника, задача достаточно сложная, сделать сравнение КПД тепловых насосов вода, грунт, воздух так же затруднительно.
Разумнее сопоставить расходы на эксплуатацию оборудования и эффективность обогрева объекта.
Воздушный тепловой насос
Установка воздушного тн обходится дешевле, но он будет потреблять много электроэнергии. Его эффективность напрямую зависит от температуры окружающей среды. В сильные морозы — ниже -25°С — такое устройство обогрев помещения не обеспечит, есть модели до -40°С.
Водяной тепловой насос
Водяные тн начнут терять эффективность в сильные морозы, внешней энергии будет недостаточно и потребуется дополнительный источник тепла.
Грунтовые тепловые насосы
Грунтовые тн работают стабильно круглый год. Температура земли на глубине является неизменной, поэтому эффективность таких устройств от поры года не зависит. Однако, для бурения скважин и обустройства коллектора необходимо вложение крупных сумм денег, поэтому установка геотермального теплового оборудования оправдана только в расчете на долгосрочную перспективу.
Расчет COP теплового насоса
СОР рассчитывают на основании показателей температуры источника (Т1) и воды в системе обогрева (Т2), по формуле: СОР = Т2/(Т2 – Т1).
Следует учитывать, что tº в этом случае измеряется в Кельвинах. К принятому у нас показателю в Цельсиях добавляют число 273 и производят дальнейшие расчеты.
Для примера: если tº земли составляет 5 градусов Цельсия, а в отопительном контуре она держится на уровне 55, сперва следует преобразовать данные в другую систему измерения: 5+273 = 278 К, 55+273 = 328 К.
СОР = 328 / (328 – 278) = 6,56.
Производя расчет COP теплового насоса, необходимо помнить, что он предполагает работу оборудования без учета потерь (при идеальных условиях). На практике значение COP будет гораздо ниже.
Температуру источника изменить невозможно, поэтому для повышения эффективности следует позаботиться о низкотемпературной системе отопления.
Возникли вопросы?
Заполните форму обратной связи, наши менеджеры свяжутся с вами!
Задать вопрос
Возврат к списку
Поделиться:
Тепловой КПД: определение, пример и двигатель
Изобретение современной паровой машины в 18 -м -м веке, несомненно, является одним из самых важных технических достижений в истории человечества.
Первые паровые двигатели, изобретенные английскими инженерами Томасом Ньюкоменом и Джеймсом Уаттом, значительно ускорили промышленную революцию и сделали Великобританию новым мировым лидером в промышленности. Интересно, однако, что теоретическое понимание того, как работали эти паровые машины, было очень неточным. Не было до 19-й -й век, когда была разработана теория тепла и движения, или термодинамика , когда французский инженер Сади Карно, обеспокоенный промышленным превосходством Британии над Францией, попытался улучшить конструкцию паровых машин, рассмотрев общую модель тепловой энергии. двигатели и их термический КПД. Это стремление к промышленной эффективности привело к созданию термодинамики как раздела теоретической физики с невероятно глубокими последствиями для нашего понимания тепла, работы и энергии. В этой статье мы углубимся в то, что такое тепловые двигатели и как мы определяем их эффективность, а затем рассмотрим цикл Карно и то, что он говорит нам о взаимосвязи между теплотой и работой.
Тепловой КПД двигателя
В этой статье мы будем рассматривать термодинамическую модель теплового двигателя, чтобы объяснить концепцию теплового КПД. Итак, прежде чем более подробно рассмотреть тепловую эффективность, давайте вспомним, что именно мы подразумеваем под тепловым двигателем.
A Тепловая машина — это термодинамическая система, преобразующая теплоту в работу.
Общая модель тепловой машины представляет собой систему, обычно состоящую из газа, находящегося между двумя тепловыми резервуарами, один из которых имеет более высокую температуру, чем система, а другой — более низкую температуру. В контексте тепловой машины мы называем эти резервуары источником тепла и поглотителем соответственно. Система способна совершать работу, обозначаемую \(W\) в окружающей среде, например, толкая поршень вверх по мере расширения газа. Именно эта работа \(W\) делает двигатель полезным, например, в автомобильном двигателе эта работа используется для поворота оси, заставляющей вращаться колеса.
Из-за разницы температур тепло передается от источника тепла к системе. Это обозначено \(Q_\mathrm{H}\) на рисунке 1. Часть этого тепла будет использована для совершения полезной работы в окружающей среде, в то время как часть тепла увеличит внутреннюю энергию газа, повысив его температуру. Затем разница температур между системой и радиатором вызовет поток тепла от системы к радиатору, при этом эта энергия обозначается \(Q_\mathrm{C}\).
Рис. 1. Обобщенная модель тепловой машины, как показано выше, позволяет определить тепловой КПД, не беспокоясь о точной природе потерь энергии.
Тепловой КПД Определение
Тепловые двигатели работают путем преобразования энергии, передаваемой в виде тепла, в полезную работу. Однако, как мы увидим, ни одна тепловая машина не является абсолютно эффективной, поэтому некоторое количество тепла всегда теряется в окружающую среду. Мы можем определить эту потерю тепла как отработанное тепло: чем меньше тепла теряется, тем эффективнее работает двигатель.
Итак, КПД двигателя определяется количеством полезной работы, совершаемой на единицу подведенного тепла. Затем можно использовать термический КПД для количественной оценки этого КПД.
Тепловой КПД \(\eta\), или Коэффициент полезного действия, — это процент подводимого тепла \(Q\), поступающего в систему, который преобразуется системой в работу \(Вт\).
\[\eta=\frac{W}{Q}.\]
Тепловой КПД может принимать значения только между \(0\) и \(1\), \(0\%-100\%\) , в чем можно убедиться, применив первый закон термодинамики к определению \(\эта\). Рассмотрим тепловложение двигателя \(Q_\text{in}\). Предполагая, что в самом двигателе энергия не теряется, любое тепло, не преобразованное в работу, будет потеряно в виде тепла \(Q_\text{out}\) в окружающую среду. Следовательно, мы можем определить проделанную работу как \[W=Q_\text{in}-Q_\text{out}.\]
Подключив это к определению теплового КПД, мы получим
\[\begin{align}\eta&=\frac{W}{Q_\text{in}}\\&=\frac{Q_\text{in} -Q_\text{out}}{Q_\text{in}}\\&=1-\frac{Q_\text{out}}{Q_\text{in}}.
\end{align}\]
Тепловой КПД может принимать значения только между \(0\) и \(1\), \(0\%-100\%\), как можно увидеть, применив первый закон термодинамики к определению для \(\eta \). Рассмотрим тепловложение двигателя \(Q_\text{in}\). Предполагая, что в самом двигателе энергия не теряется, любое тепло, не преобразованное в работу, будет потеряно в виде тепла \(Q_\text{out}\) в окружающую среду. Следовательно, мы можем определить проделанную работу как \[W=Q_\text{in}-Q_\text{out}.\]
Подключив это к определению теплового КПД, мы получим
\[\begin{align}\eta&=\frac{W}{Q_\text{in}}\\&=\frac{Q_\text{in} -Q_\text{out}}{Q_\text{in}}\\&=1-\frac{Q_\text{out}}{Q_\text{in}}.\end{align}\]
Первый закон термодинамики гарантирует, что тепло, теряемое системой, не может быть больше, чем тепло, поступающее в систему, и поэтому \(0\leq\eta\leq1\).
Первый закон термодинамики гласит, что изменение внутренней энергии системы \(\Delta U\) всегда должно быть равно разнице между теплом, подведенным к системе \(Q\), и работой выполняется системой в ее среде \(W\).
\[\Delta U=Q-W.\]
Давайте рассмотрим пример.
Если тепловой двигатель, который работает, поглощая \(500\,\mathrm{Дж}\) тепла, теряет \(200\,\mathrm{Дж}\) тепла в окружающую среду во время своего цикла, что тепловой КПД этого двигателя?
Ответ:
Используя приведенную выше формулу:\[\begin{align}\nu&=1-\frac{Q_\text{out}}{Q_\text{in}}\\&=1-\frac {200\,\mathrm{J}}{500\,\mathrm{J}}\\&=0,6 \quad \text{или}\quad 60\%.\end{align}\]
Как вы знаете, если вы когда-либо видели перегрев двигателя автомобиля, большинство тепловых двигателей крайне неэффективны. Например, средний дизельный двигатель работает с КПД около \(25\%\), а даже самый эффективный из тепловых двигателей может достигать только \(50\%-60\%\). Большая часть этой неэффективности связана с потерями тепла и силами трения внутри двигателя, а также с потерями в процессе сгорания. Однако, как мы увидим при исследовании цикла Карно, совершенная эффективность невозможна даже для идеализированных Реверсивные двигатели в соответствии с 2 и Законом термодинамики.
Пример тепловой эффективности
Многие устройства и технологии, необходимые в современном обществе, основаны на этой простой модели теплового двигателя, и повышение эффективности этих устройств может помочь снизить потребление энергии. Например, при покупке холодильника перед покупкой важно сравнить коэффициент полезного действия (КПД) разных моделей. Холодильник представляет собой своего рода тепловую машину в обратном направлении, в которой работа, выполняемая окружающей средой в системе, обычно в виде компрессора, для извлечения тепла из холодного резервуара (внутри холодильника) и откачки его в горячий резервуар (наружная комната).
Рис. 2. Холодильник можно рассматривать как тепловую машину, работающую в обратном направлении, извлекающую тепло из холодного резервуара и перекачивающую его в горячий резервуар, совершая работу.
Это означает, что для холодильников КПД определяется обратно пропорционально тепловому КПД тепловой машины, так как в данном случае нас интересует, сколько тепла может быть извлечено за единицу работы.
Здесь «отработанное» тепло — это тепло, переданное в систему окружающей средой \(Q_\text{in}\).
\[\begin{align}COP &= \frac{Q_\text{out}}{W_\text{in}} \\&=\frac{Q_\text{out}}{Q_\text{in }-Q_\text{out} }\\&=\frac{Q_\text{out}}{Q_\text{in}}-1\end{align}\]
Это означает, что, в отличие от теплового КПД, КПД может принимать значения больше единицы, чем выше КПД, тем больше тепла отводится за единицу работы.
Среднестатистический современный холодильник работает с КПД \(1,37.\) Если мощность холодильника составляет \(300\,\mathrm{Вт}\), сколько тепла извлекается из внутренней части холодильника за одна минута?
Ответ:
Во-первых, нам нужно рассчитать, какую работу совершает холодильник за одну минуту, это можно найти из определения мощности.\[\begin{align}\text{Power}&=\frac {\text {Выполненная работа}}{\text {Время}}\\ подразумевает \text{Выполненная работа}=\text{Мощность}\cdot\text{Время}\\\ подразумевает W&=300\,\mathrm{W }\cdot60\,\mathrm{s}\\&=18000\,\mathrm{J}\end{align}\]
Сочетание этого с определением COP дает нам количество удаленного тепла\[\begin{align}Q_\text{out}&=COP\cdot W\\&=1,37\cdot18\,000\,\mathrm{J} \\&=24\,660\,\mathrm{J}\end{align}\]
Тепловой КПД цикла Карно
Мы коснулись идеи, что даже для идеализированной обратимой тепловой машины \( 100\%\) КПД невозможен.
Впервые это понял французский физик и инженер Сади Карно, который установил верхний предел теплового КПД тепловой машины, рассмотрев идеальный термодинамический процесс, теперь известный как цикл Карно.
Рис. 3. Сади Карно (1796-1832) получил прозвище «Отец термодинамики» благодаря своей работе над тепловыми двигателями и тепловым КПД.
Цикл Карно является наиболее эффективной тепловой машиной, потому что это обратимый процесс. В обратимом процессе энергия не теряется в окружающую среду или из-за диссипативных сил, таких как трение. Определяющей чертой обратимого процесса является отсутствие изменения чистой энтропии в системе в конце процесса.
А обратимый термодинамический процесс — это процесс, который переводит систему из некоторого начального состояния через цикл различных термодинамических состояний, прежде чем вернуть ее обратно в точное начальное состояние.
Обратимых процессов в природе не наблюдается, так как практически невозможно предотвратить возникновение сил трения как между самими молекулами жидкости, так и внутри компонентов системы, таких как поршень в тепловом двигателе.
Таким образом, цикл Карно не является работающей тепловой машиной, однако он предлагает простую иллюстрацию взаимосвязи между такими величинами, как теплота, работа и температура в тепловых машинах. Давайте теперь посмотрим на особенности цикла Карно.
Цикл Карно
Цикл Карно рассматривает тепловую машину, описанную в начале этой статьи, в которой идеальный газ удерживается между двумя тепловыми резервуарами, один при \(T_\mathrm{H}\), а другой при \( T_\mathrm{C}\), с \(T_\mathrm{H}>T_\mathrm{C}\). Работа может совершаться газом над окружающей средой (или наоборот) с помощью подвижного поршня. Цикл состоит из четырех различных термодинамических процессов: изотермического расширения, изэнтропического расширения, изотермического сжатия и изэнтропического сжатия. Этот список довольно громоздкий, поэтому давайте рассмотрим некоторые определения. Во-первых, сжатие и расширение относятся к влиянию процесса на объем газа.
Сжатие — Процесс уменьшения объема газа за счет того, что среда совершает над ним работу.
В случае с тепловым двигателем эта работа выполняется за счет перемещения поршня вниз.
Расширение — Процесс увеличения объема газа за счет выполнения им работы над окружающей средой. В тепловом двигателе газ расширяется, толкая поршень вверх.
В то время как изотермические и изоэнтропические относятся к условиям, при которых происходит процесс, и какое количество остается постоянным на всем протяжении.
Изотермический — Термодинамический процесс, во время которого система поддерживает постоянную температуру.
Изэнтропический — Это обратимый адиабатический процесс, означающий, что нет чистого изменения энтропии в конце процесса (обратимый) и что между системой и окружающей средой не происходит теплообмена на протяжении всего процесса (адиабатический).
Имея в виду эти определения, давайте пройдемся по четырем стадиям цикла Карно.
Изотермическое расширение: Изначально идеальный газ находится в тепловом контакте с горячим резервуаром, будучи теплоизолированным от холодного резервуара.
Температура газа бесконечно меньше, чем в горячем резервуаре, что позволяет передавать тепло без какого-либо изменения температуры газа. Эта передача тепла \(Q_\mathrm{H}\) заставляет газ расширяться, при этом вся тепловая энергия расходуется на работу, толкающую поршень вверх, поэтому температура не меняется. Согласно закону идеального газа, при расширении газа при постоянной температуре происходит соответствующее падение давления. Теплоперенос соответствует увеличению энтропии газа.\[\Delta S_\mathrm{H}=\frac{Q_\mathrm{H}}{T_\mathrm{H}}.\]
Изэнтропическое расширение: Затем газ термически изолирован от оба резервуара, поэтому передача тепла не может происходить. Однако расширение продолжается из-за увеличения давления, заставляющего газ совершать работу над поршнем. Эта работа, совершаемая газом, вызывает уменьшение его внутренней энергии, поэтому газ охлаждается до температуры бесконечно малой, превышающей \(T_\mathrm{C}\). Поскольку нет теплопередачи, энтропия не меняется.
Изотермическое сжатие: Теперь газ термически изолирован от горячего резервуара, но находится в тепловом контакте с холодным резервуаром. Поршень работает над газом, сжимающим его, при этом вся эта работа преобразуется в отработанное тепло \(Q_\mathrm{C}\), теряемое в холодном резервуаре, поэтому температура не меняется. Сжатие при постоянной температуре вызывает увеличение давления. Существует уменьшение энтропии газа, определяемое выражением \(\Delta S_\mathrm{C}=\frac{Q_\mathrm{C}}{T_\mathrm{C}}\).
Изэнтропическое сжатие: Газ снова термически изолирован от обоих резервуаров, при этом работа над ним продолжается со стороны окружающей среды. Эта работа, совершаемая над газом, увеличивает внутреннюю энергию газа, повышая температуру до бесконечно малого значения, меньшего, чем \(T_\mathrm{H}\), и возвращая систему в исходное состояние. В этой точке энтропия не меняется, так как нет теплопередачи.
Температура газа бесконечно меньше, чем в горячем резервуаре, что позволяет передавать тепло без какого-либо изменения температуры газа. Эта передача тепла \(Q_\mathrm{H}\) заставляет газ расширяться, при этом вся тепловая энергия расходуется на работу, толкающую поршень вверх, поэтому температура не меняется. Согласно закону идеального газа, при расширении газа при постоянной температуре происходит соответствующее падение давления. Теплоперенос соответствует увеличению энтропии газа.
Цикл Карно часто представляют в виде замкнутой траектории вокруг графика давление-объем, как показано на рис.
3. Кривая AB следует по траектории при фиксированной температуре, известной как изотерма , представляющая начальное изотермическое сжатие. BC представляет собой адиабатическое сжатие, наблюдаемое по тому факту, что на этом пути отсутствует теплообмен. Затем цикл завершается кривой CD, следующей за изотермой более низкой температуры, прежде чем DA возвращает систему в исходное состояние. Обратите внимание, что работа, выполненная системой, определяется площадью, ограниченной кривой.
Рис. 3. Цикл Карно может быть представлен в виде замкнутой кривой на графике давление-объем, как показано выше. Шаг 1 следует по кривой AB, шаг 2 следует по кривой BC, шаг 3 следует по CD, а шаг 4 следует по DA.
Итак, что этот цикл может рассказать нам о тепловом КПД тепловой машины? Что ж, давайте сначала посмотрим, как меняется энтропия системы на протяжении всего процесса. Как обратимый процесс, в цикле Карно не может быть никакого изменения чистой энтропии. Отсюда \[\Delta S_\mathrm{H}+\Delta S_\mathrm{C}=\Delta_{\text{net}}=0\]
Применяя определение энтропии, \(\Delta S=\frac {Q}{T}\), мы находим связь между теплотой, передаваемой между системой и тепловыми резервуарами, и температурой этих тепловых резервуаров.
\[\begin{align}\frac{Q_\mathrm{H}} {T_\mathrm{H}}+\frac{Q_\mathrm{C}}{T_\mathrm{C}}&=0\\\ подразумевает \frac{Q_\mathrm{H}}{T_\mathrm{H }}&=-\frac{Q_\mathrm{C}}{T_\mathrm{C}}\\\ подразумевает \frac{Q_\mathrm{C}}{Q_\mathrm{H}}&=-\frac {T_\mathrm{C}}{T_\mathrm{H}}\end{align}\]
Применение этого к определению эффективности дает \[\eta=1+\frac{Q_\mathrm{C}}{Q_\mathrm{H}}=1-\frac{T_\mathrm{C}}{T_ \mathrm{H}}.\]
Это основное свойство обратимых тепловых двигателей, их эффективность определяется только температурами резервуаров, между которыми они работают. Чем больше соотношение между \(T_\mathrm{H}\) и \(T_\mathrm{C}\), при \(T_\mathrm{C}термодинамике. \mathrm{h}\)>
Если обратимая тепловая машина работает между двумя тепловыми резервуарами, один при \(T_1=300\,\mathrm{K}\) и один при \(T_2=400\,\mathrm{K}\), каков его тепловой КПД?
Ответ:
Используя приведенное выше уравнение, мы находим эффективность как \[\begin{align}\eta&=1-\frac{T_1}{T_2}\\&=1-\frac{300\,\ mathrm{K}}{400\,\mathrm{K}} \\&=25\%.
\end{align}\]
2
nd Закон тепловой эффективности
Сэди Карно поняла, что из-за отсутствия любой потери энергии в обратимом двигателе, КПД обратимого теплового двигателя является максимально возможным КПД любого теплового двигателя. Это было резюмировано в его весьма влиятельной теореме.
Теорема Карно утверждает, что тепловая машина, работающая между двумя тепловыми резервуарами \(T_\mathrm{H},T_\mathrm{C}\), не может иметь КПД больше, чем у обратимой тепловой машины (тепло Карно двигатель), работающий между одними и теми же двумя температурами.
Как мы видели, КПД обратимой тепловой машины определяется только температурами тепловых резервуаров, между которыми она работает.
\[\eta=1-\frac{T_\mathrm{C}}{T_\mathrm{H}}.\]
Это уравнение говорит нам, что единственный способ для \(\eta\) равняться единице, если \(T_\mathrm{C}=0\,\mathrm{K}\), известный как абсолютный нуль. Однако третий закон термодинамики запрещает любой системе когда-либо достигать абсолютного нуля, поэтому мы видим, что наша обратимая тепловая машина не может иметь идеальный КПД.
Третий закон термодинамики гласит, что термодинамическая система не может достичь абсолютного нуля за конечное число шагов
Итак, если двигатель Карно не может иметь КПД, равный единице, по третьему закону , и никакой тепловой двигатель не может иметь больший КПД, чем двигатель Карно, по теореме Карно, то все двигатели должны иметь тепловой КПД меньше единицы.\[\begin{align}\eta&<1\\\frac{W} {Q_\text{in}}&<1\\W& Это показывает, что тепловая энергия никогда не может быть полностью преобразована в работу во время циклического процесса, такого как тепловой двигатель. Этот факт известен как заявление Кельвина о втором законе термодинамики. Заявление Кельвина о 2 nd Законе термодинамики: Невозможно полностью преобразовать тепло во время циклического процесса. Прежде чем рассчитать тепловую эффективность цикла Ренкина, давайте разберемся с циклом Ренкина. Цикл Ренкина — это теоретический цикл, в котором тепловая энергия превращается в работу. Роли 1–2: Работа, выполняемая турбиной 2–3: Отвод тепла в градирне 3–4: Насос 4–1: Подвод тепла в котле Рабочей жидкостью в цикле Ренкина является вода. Вода проходит следующий процесс в Цикле. C-D, D-F, F-G, G-C являются определяющими процессами в цикле Ренкина. Термический КПД цикла Ренкина: Термический КПД цикла Ренкина представляет собой отношение работы, произведенной паровой турбиной, уменьшенной за счет работы насоса, к поступающему теплу. энергии от котла. Тепловая энергия топлива передается рабочему телу, т.е. воде. Теплотворная способность, поглощаемая водяным паром, может быть рассчитана по следующей формуле: Qin = m (hF — hD) Перегретый пар, произведенный котлом, затем поступает в паровую турбину. Затем тепловая энергия водяного пара преобразуется в кинетическую энергию, показанную линией F-G на изображении выше. Уменьшение энтальпии можно использовать для расчета величины энергии движения, производимой паровой турбиной, по следующей формуле: Пар, выходящий из паровой турбины, поступает в конденсатор для конденсации обратно в жидкую фазу. Тепловой КПД – основные выводы
Распространенной моделью тепловой машины является газ, находящийся в тепловом контакте с двумя резервуарами, один из которых имеет более высокую температуру, чем газ \(T_\mathrm{H}\), а другой — более низкую температуру \(T_\mathrm{C}\). ).
Каталожные номера
Как рассчитать тепловую эффективность цикла Ренкина | Асвини Пало
Цикл Ренкина:
Цикл Ренкина разработан Уильямом Джоном Маккорном Ренкином в 19 веке. Он широко используется во всех видах паровых двигателей.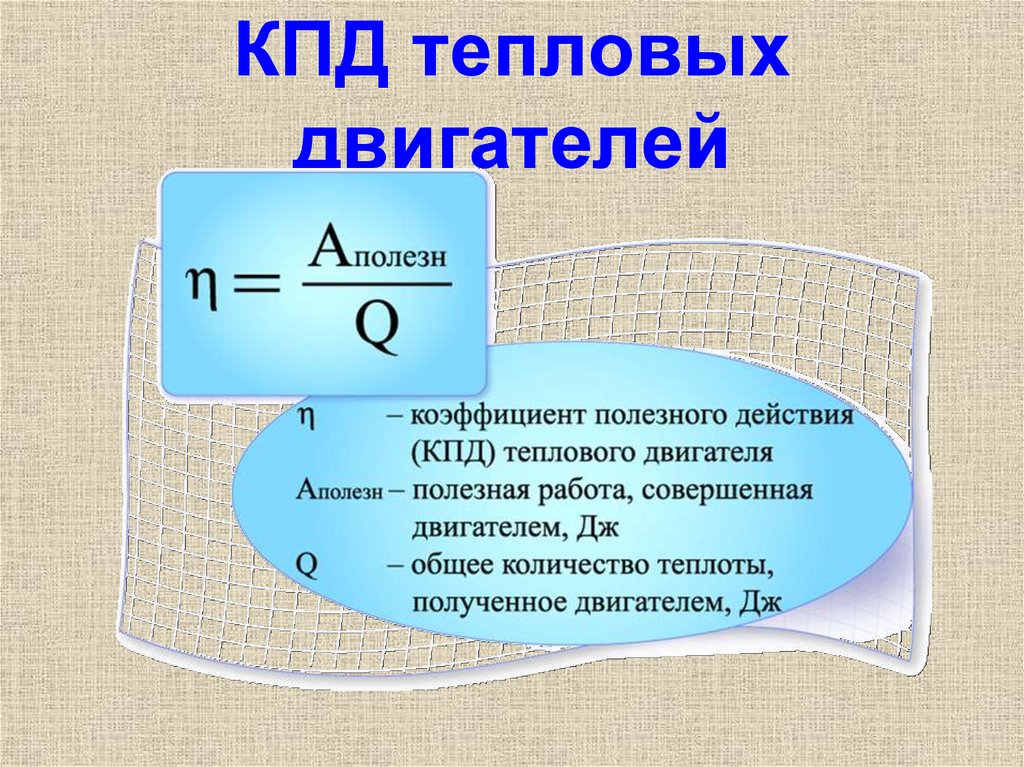
Расчет теплового КПД цикла Ренкина:
Wout = m (hF — hG) 