Содержание
Какую работу совершает газ при переходе из состояния 1 в состояние 3
Прочее › Находится › В сосуде находится некоторое количество идеального газа во сколько раз изменится температура газа
Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в килоджоулях.) Ответ: 8.
- Как найти работу которую совершает газ
- Какую работу совершает газ расширяясь при постоянном давлении 200 Килопаскаль от объёма 1 6 л до 2 6 л
- Что значит газ совершает работу
- Как понять когда газ совершает отрицательную работу
- Какую работу совершит газ расширяясь при постоянном давлении 304 кпа от объема 3 л до объема 18 л
- Как зависит давление от объёма газа
- Чему равна работа газа при изохорном процессе с постоянным давлением 100 кпа *
- В каком из процессов газ совершает наибольшую работу
- В каком процессе работа газа равна нулю
- Когда работа над газом
- Какую работу совершает газ при переходе из состояния 1 в состояние 3 Ответ дайте в Килоджоулях ответ
- Какую работу совершает газ за один цикл
- Чему равна работа газа при Изохорном переходе системы
- Как определить работу по сжатию газа
- Как найти работу газа при расширении
- Как геометрически можно определить работу газа
- Как найти работу
Как найти работу которую совершает газ
В изобарном процессе (p = const) работа, совершаемая газом, выражается соотношением: A = p (V2 — V1) = pΔV. В изотермическом процессе температура газа не изменяется, следовательно, не изменяется и внутренняя энергия газа, ΔU = 0.
В изотермическом процессе температура газа не изменяется, следовательно, не изменяется и внутренняя энергия газа, ΔU = 0.
Какую работу совершает газ расширяясь при постоянном давлении 200 Килопаскаль от объёма 1 6 л до 2 6 л
Ответ: Расширяясь, газ должен был выполнить работу в 200 Дж.
Что значит газ совершает работу
Газ, находящийся в сосуде под поршнем, действует на поршень с силой F = pS, где p давление газа, S площадь поршня. Если при этом поршень перемещается, то газ совершает работу.
Как понять когда газ совершает отрицательную работу
Очевидно, работа газа положительна, если газ расширяется, и отрицательна, если газ сжимается.
Какую работу совершит газ расширяясь при постоянном давлении 304 кпа от объема 3 л до объема 18 л
Решение: Работа газа определяется выражением: A = p · ∆ V = p · (V 2 − V 1) = 304 · 10 3 · (18 · 10 − 3 − 3 · 10 − 3) = 304 · 10 3 · 15 · 10 − 3 = 4560 = 4.56 кДж.
Как зависит давление от объёма газа
При уменьшении объёма газа его давление увеличивается, а при увеличении объёма — давление уменьшается (при условии, что масса и температура газа остаются неизменными).
Чему равна работа газа при изохорном процессе с постоянным давлением 100 кпа *
Ответ: Работа, совершенная газом в изобарном процессе, равна 200 Дж.
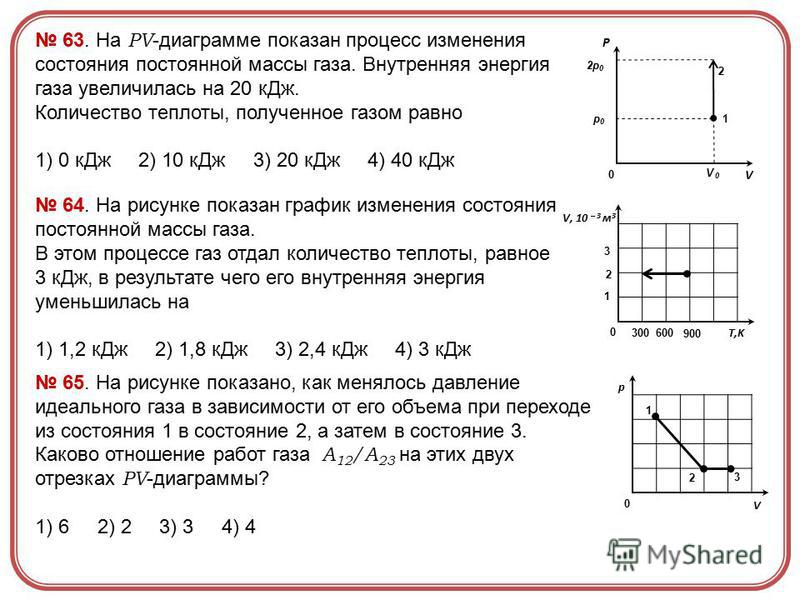
В каком из процессов газ совершает наибольшую работу
Поэтому в процессе 2-3 газ и совершает наибольшую по абсолютной величине (среди рассматриваемых процессов) работу (ответ 2.).
В каком процессе работа газа равна нулю
Изохорный процесс.
При изохорном нагревании или охлаждении (соответственно, прямые 1–2 и 1–3 на рис. 2.7) работа просто равна нулю, поскольку объем не меняется.
Когда работа над газом
Если нагревать газ, то он начинает увеличивать объем, а поршень от увеличения объема начинает отходить назад, следовательно ГАЗ СОВЕРШАЕТ работу.
Какую работу совершает газ при переходе из состояния 1 в состояние 3 Ответ дайте в Килоджоулях ответ
Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в килоджоулях.) Ответ: 8.
Какую работу совершает газ за один цикл
Работа газа за цикл численно равна площади фигуры, ограниченной графиком цикла на диаграмме pV.
Чему равна работа газа при Изохорном переходе системы
Изохорный процесс — это процесс, происходящий при постоянном объёме. То есть в этом процессе газ не расширяется и не сжимается, а значит не совершается работа ни газом, ни над газом, тогда Аг = 0 и первый закон термодинамики приобретает вид: ΔU = Q.
Как определить работу по сжатию газа
A = p * ΔV, где р — давление газа (Па), ΔV = (V₂ — V₁) — объём (м³). A = Q При изотермическом процессе.
Как найти работу газа при расширении
Работа изображается площадью криволинейной трапеции под графиком процесса (рис. 58). ΔA=P(V2–V1).
Как геометрически можно определить работу газа
Работу газа можно определить графически. Изобразим график зависимости давления газа от его объёма при р = const (рис. 68). Если процесс перехода газа из начального состояния в конечное является изобарным (АВ — изобара), то работа силы давления газа численно равна площади прямоугольника V1АВV2.
Как найти работу
Как искать работу: пять самых популярных способов:
- Знакомства Интересную работу в своей сфере можно найти через коллег.

- Кадровое агентство
- Объявления в соцсетях
- Сайты по поиску работы
- Профессиональные сообщества
- Биржа труда
Задание 8 из ЕГЭ по физике
Все для самостоятельной подготовки к ЕГЭ
Зарегистрироваться
Русский язык
Математика (профильная)
Математика (базовая)
Обществознание
Физика
История
Биология
Химия
Английский язык
Литература
Информатика
География
Задания
Варианты
Теория
Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
Задание 6
Задание 7
Задание 8
Задание 9
Задание 10
Задание 11
Задание 12
Задание 13
Задание 14
Задание 15
Задание 16
Задание 17
Задание 18
Задание 19
Задание 20
Задание 21
Задание 22
Задание 23
Задание 24
Задание 25
Задание 26
Задание 27
Задание 28
Задание 29
Задание 30
За это задание вы можете получить 1 балл на ЕГЭ в 2023 году
Разбор сложных заданий в тг-канале:
Посмотреть
Задача 1
Какую работу совершат 6 кг воздуха, расширяясь при изобарическом нагреве от 5◦С до 150◦С? Ответ выразите в (кДж) и округлите до целых.
Задача 2
На pV -диаграмме представлен процесс изменения состояния идеального одноатомного газа. Масса газа не меняется. Какую работу совершает газ при переходе из состояния 1 в состояние 3?…
Задача 3
На pT -диаграмме представлен процесс изменения состояния идеального одноатомного газа. Масса газа не меняется. Какую работу совершают внешние силы при переходе газа из состояния 1 …
Задача 4
Какую работу совершил газ при переходе из состояния 1 в состояние 3? Ответ выразите в (·p0V0).
Задача 5
При изобарном расширении идеальный двухатомный газ получил количество теплоты, равное 800 Дж. Насколько увеличилась внутренняя энергия газа при этом процессе? Ответ выразите в (Дж)…
Задача 6
Какова внутренняя энергия гелия, заполняющего аэростат объёмом 60 м3 при давлении 100 кПа? Ответ выразите в (МДж).
Задача 7
Аргону сообщили 30 кДж теплоты, и он изобарно расширился. При этом объём газа увеличился на 0,6 м3. Каково давление газа? Ответ выразите в (кПа).
Задача 8
В сосуде с постоянным объёмом охлаждают идеальный одноатомный газ, причём количество отведённого тепла равно 300 Дж. Определите объём сосуда, если давление в нём понизилось на 100 …
Задача 9
В изобарном процессе при нормальном атмосферном давлении объём одноатомного газа увеличился от 5 л до 7 л. На сколько увеличилась внутренняя энергия газа в данном процессе? Ответ в…
Задача 10
Газ совершает процесс, при котором работа газа равна убыли его внутренней энергии. Что это за процесс? Ответ запишите словом.
Задача 11
КПД двигателя, работающего по циклу Карно, составляет 40 %. Какова температура нагревателя, если температура холодильника 127 $°$С? Ответ представьте в $◦$С и округлите до целого.
Задача 12
Каков КПД идеальной тепловой машины, работающей в интервале температур 100 $°$С–400 $°$С?Ответ выразите в процентах и округлите до целых. Ответ в %.
Задача 13
За цикл тепловая машина получила 100 Дж теплоты. Найдите, сколько теплоты получил холодильник, если коэффициент полезного действия этой машины 24%. Ответ в Дж.
Задача 14
Один моль идеального одноатомного газа сначала изотермически сжали при температуре 270 К до объёма 0,831 м3. Затем газ изохорно охладили, понизив давление в 2 раза. Какую работу со…
Задача 15
Какое количество теплоты получает идеальный одноатомный газ в изобарном процессе, если он совершает работу против внешних сил, равную 2 кДж? Ответ в кДж.
Задача 16
Какую работу совершает газ в ходе изохорического процесса, если он при этом отдаёт 3,6 кДж тепла? Ответ в кДж.
Задача 17
Каков КПД тепловой машины, работающей по циклу Карно, если отношение работы изотермического расширения к модулю работы изотермического сжатия равно 4? Ответ в %.
Задача 18
Температура нагревателя идеальной тепловой машины 600$°$C, а холодильника 100$°$C. Чему равен её коэффициент полезного действия? Ответ выразите в % и округлите до целых.
Задача 19
На рисунке приведён график зависимости давления неизменной массы газа от температуры. Изменения происходят в направлении указанном стрелками. Какой процесс происходит с газом на уч…
Задача 20
Каково давление одноатомного идеального газа, занимающего объём 2 л, если его внутренняя энергия равна 300 Дж? Ответ в кПа.
1
2
3
4
5
. ..
..
7
Задание 8 ЕГЭ по физике посвящено тепловому равновесию и уравнению состояния. Разработчики разделили все варианты вопросов на две примерно равные части. Первая из них посвящена уравнению Клапейрона-Менделеева, вторая — основному уравнению МКТ (молекулярно-кинетической теории). Это уравнение объясняет зависимость макроскопических параметров (давления, объёма, температуры) жидкостей и газов, и для успешного ответа на этот вопрос ученику придется предварительно повторять материал всего курса физики из средней и старшей школы.
Все варианты задания 8 ЕГЭ по физике построены одинаково: учащемуся предлагается текстовое (к примеру, «абсолютная температура газа уменьшилась в два раза, в то время, как концентрация молекул увеличилась в два раза»), графическое или табличное описание какого-либо процесса, происходящего в веществе. Ученик должен ответить на конкретно поставленный вопрос, рассчитав нужное числовое значение и записав его в качестве краткого ответа. Если ответом является десятичная дробь, в задании будет обязательно оговорено условие ее округления.
Если ответом является десятичная дробь, в задании будет обязательно оговорено условие ее округления.
Несмотря на то, что тема молекулярно-кинетической теории обычно нелюбима школьниками, задание № 8 ЕГЭ по физике обычно не вызывает у экзаменуемых никаких сложностей. Однако затягивать с его решением не стоит, так как время на прохождение всего испытания ограничено регламентом.
<< Задание 7
Задание 9 >>
Популярные материалы
Составим твой персональный план подготовки к ЕГЭ
Термодинамика
Термодинамика
ФИЗИКА 1151
Глава 18, Термодинамика
| ТУ,
Глава 18 | Курс
Календарь |
D18.1 Идеальный газ запечатан в жестком контейнере при 25°C и 1,0
банкомат Какой будет его температура при увеличении давления до 2,0 атм?
Каким будет его давление при повышении температуры до 50°С
Закон идеального газа
PV = nRTНаходясь в жестком контейнере, объем газа изменяется , а не ;
V = V или = константа.Это означает, что мы можем использовать закон идеального газа как
.
Т/П = Т или /П илиили
T = P [T o /P o ] = [P/P o ]
Т илиПомните, эти температуры должны быть абсолютными температурами,
T o = 25°C = 302 K
T = [ P / P o ] T o = [ 2,0
атм / 1,0 атм ] [302
К] = [ 2 ] [ 302 К] = 604 КТ = 604 К = (604 — 273)°С = 331°С = Т
Или, хотя V = const, мы можем записать закон идеального газа как
П/Т = П или / Т илиили
P = T [P o / T o ] = [T / T o ]
Р илиПомните, эти температуры должны быть абсолютными температурами, измеренными
в Кельвинах, К.T o = 25°C = 302 K и T = 50°C = 327 K
P = [ T / T o
] P илиР = [ 327 К / 302
К ] (1 атм)P = 1,08 атм
Д18. 2 Газ на 1,5 атм расширяется от 2,5 литров
до 3,5 литров. Какую работу совершает газ?
Работа — это площадь под кривой на p-V диаграмме; для постоянного давления,
Это
Вт = p В
Вт = (1,5 атм)(1,0 л)
Вт = 1,5 атм-л = 1,5 л-атмХотя это, безусловно, верно, требуется преобразование в джоули,
1 л-атм = ( 10 — 3 м 3 ) (1,013 x 10 5 N / м 2)
= 1,013 x 10 2 Н·м = 101,3 ДжВт = 1,5 л-атм [ 101,3 Дж / 1
л-атм ] = 152 Дж = ВтВт = 152 Дж
D18.
3 При постоянном давлении 1,5 атм газ
расширяется с 2,0 литров до 3,0 литров, при этом в него поступает 500 Дж энергии.
а) Какую работу совершает газ?
(б) Как изменится его внутренняя энергия?Часть (a) этого вопроса идентична вопросу 14.17. Мы готовы
знать ответ на этот вопрос; работа, совершаемая газом, равна
Вт = 152 Дж
Поскольку газ совершает работу 152 Дж, он поглощает или получает 500 Дж энергии. Что
означает, что его чистое увеличение внутренней энергии равноE Интервал
= Q — Вт = 500 Дж — 152 Дж = 348 Дж
E инт
= 348 Дж
D18.4 При постоянном давлении 2,25 ат газ сжимают с 2,00
л до 1,50 л, при этом 375 Дж энергии уходит из газа.
а) Какую работу совершает газ ?
(б) Как изменится его внутренняя энергия?Работа — это площадь под кривой на p-V диаграмме; для постоянного давления,
этоВт = p В
Вт = (2,25 атм) (- 0,50 л)
Вт = — 1,125 л-атмВт = — 1,125 л-атм [ 101,3 Дж / 1
л-атм ] = — 114 Дж
Так как газ совершает работу W = -114 Дж (что эквивалентно 114 Дж
работы, выполненной на ), он также отдает 375 Дж энергии (что означает
Q = — 375 Дж).Это означает, что его чистое изменение внутренней энергии равно
.
Е интервал
= Q — W = — 375 Дж — (- 114 Дж)
E инт
= — 261 ДжD18.5 После 1,0 моль идеального газа первоначально при
0 °C и 1,0 атм расширяют изотермически до удвоенного исходного объема,
он сжимается изобарически обратно до исходного объема. Что
чистая работа, выполненная газом или над ним? Какова его конечная температура?
Для этого требуется диаграмма p-V.
Когда газ расширяется изотермически из состояния 1 в состояние 2 ,
работа, совершаемая газом, определяется уравнением 14.17,
W изотерма = n R T ln [V f / V i ]или
W изотерма = n R T ln [V 2 / V 1 ]Из условия задачи мы знаем
В 2 = 2 В 1Отсюда мы можем вычислить работу, совершенную газом,
Вт изотерма = (1,0 моль)(8,314 Дж / моль-К )
(273 К) лн [2 В 1 / В 1 ]
Вт изотерма = (1,0 моль)(8,314 Дж / моль-К
(273 К) ln [ 2 ]
Вт изотерма = (1,0 моль)(8,314 Дж / моль-К
) (273 К) 0,693Вт изотерма = 1,573 Дж
Это площадь под кривой от состояния 1 до состояния 2
При сжатии газа из состояния 2 в состояние 3 совершенная работа
это, как всегда, площадь под кривой.
Вт изобара = p В
= p (V o — 2 V o ) = — p V oМы должны найти p, давление для состояния 2 или состояния 3 . С
мы получили состояние 2 путем изотермического расширения из состояния 1 ,
мы знаем, что температура в состоянии 2 должна быть такой же, как и в состоянии 1 ;
T 1 = T 2 = 273 K. Тогда мы можем применить закон идеального газа
или, проще говоря, просто используйте
pV = константа (для постоянной T)
p 2 V 2 = p 1 V 1
p 2 = p 1 (V 1 / V 2 ) = (1,0 атм)
(V 1 / 2 V 1 ) = 0,5 атм = p 2
p 2 = p 1 ( 1 / 2
) = 0,5 атмЧтобы найти проделанную работу, W изобар = — pV o , нам нужна числовая
значение для V o , начальный объем.Мы могли бы также назвать это V 1 ,
том в состоянии 1 . Чтобы найти этот начальный объем V или или
V 1 , мы используем закон идеального газа,
pV = нРТОпять же, помните, что температура часто указывается в градусах Цельсия, потому что
это «удобно», но температуры в законе идеального газа должны
быть абсолютных температур или температур по шкале Кельвина!
pV = nRT
(1,0 атм) (V o ) = (1,0 моль) (8,314 Дж / моль-К )
(273 К)
(1,0 атм) [ (1,013 x 10 5 N / м 2)/атм.
] (V o ) = (1,0 моль) (8,314 Дж / моль-К
) (273 K)
[ 1,013 x 10 5 N / м 2
] (V o ) = (1,0 моль)(8,314 Дж / моль-К
) (273 К)
В o = 2,24 х 10 — 2 м 3
В 1 = В o = 2,24 х 10 9 м 80 — 9007 3Теперь мы можем вернуться к вычислению работы, совершаемой газом,
W изобар = — p V o = — (0,5 атм)(2,24 x 10 — 2
m 3 )
W изобар = — p V o = — (0,5 x 1,013 x 10 5 N / m 2 )(2,24
x 10 — 2 м 3 )
Вт изобар = — 1,135 Дж
Теперь мы можем сложить эти два количества работы вместе для сети
работа выполнена.Вт нетто = Вт 12 + W 23
W нетто = W изотерма + W изобара
W нетто = 1,573 Дж + (-1,135 Дж) 9 Дж нетто 32Эта работа net представляет собой область, показанную на графике выше.
D18.5 Тепловая машина поглощает 6 Дж от источника тепла и производит 2 Дж энергии
механическая работа. Какова его эффективность?
Эфф = Вт/Q ч
Eff = 2 Дж / 6 Дж = 0,33
Eff = 0,33
D19.6 Реверсивная тепловая машина с КПД
15 процентов совершают работу 180 Дж. Сколько тепла он поглощает от горячего
резервуар?
Eff = Вт / Q ч
Q ч = Вт / Eff
Q ч = 180 Дж / 0,15
Q ч = 1200 Дж
D18.
7 Двигатель Карно работает с горячим баком 650°C
при КПД 0,30. Какая должна быть температура, чтобы иметь КПД 0,35?
это водохранилище быть?Помните, что все эти температуры должны быть абсолютными температурами.
Это означает, что для нашего первоначального двигателя Карно
Т ч = 650°С = (650 + 273) К = 923 КСначала найдите T c температуру холодного резервуара. Что будет
оставаться прежним.
EFF = 1 — T C /T H = 0,30
T C /T H = 1 — 0,30 = 0,70
T C = 0,70 T H = (0,70) (923 K) = 646 K
( T c = 373°C )Теперь, при таком холодном резервуаре (T c = 646 K), какая температура
для горячего резервуара (T h = ?) даст КПД 0,35?
Eff = 1 — T c / T h = 0,35
T c / T h = 1 — 0,35 = 0,65
T h = T c /0,65Т ч = 646 К / 0,65
T h = 993 K
( T h = 620°C )
D18.
8 КПД бензинового двигателя 0,55. Оценить температуру
выхлопных газов, если выхлопные газы выходят из двигателя при температуре 125°C.до оценка работа реального двигателя, как
бензиновый двигатель, мы можем относиться к нему как к реверсивному двигателю или двигателю Карно.
Для такого двигателя Карно КПД равен.
Эфф = 1 — Т с / Т чВыхлопные газы уходят при холодной температуре Т c
= 125°С = 398 КT c / T h = 0,55
T c / T h = 1,0 — 0,55 = 0,45Т ч = 398 К / 0,45
T h = 884 K
( T h = 611°C )
| Возврат
в Календарь |
(с) 2000 г.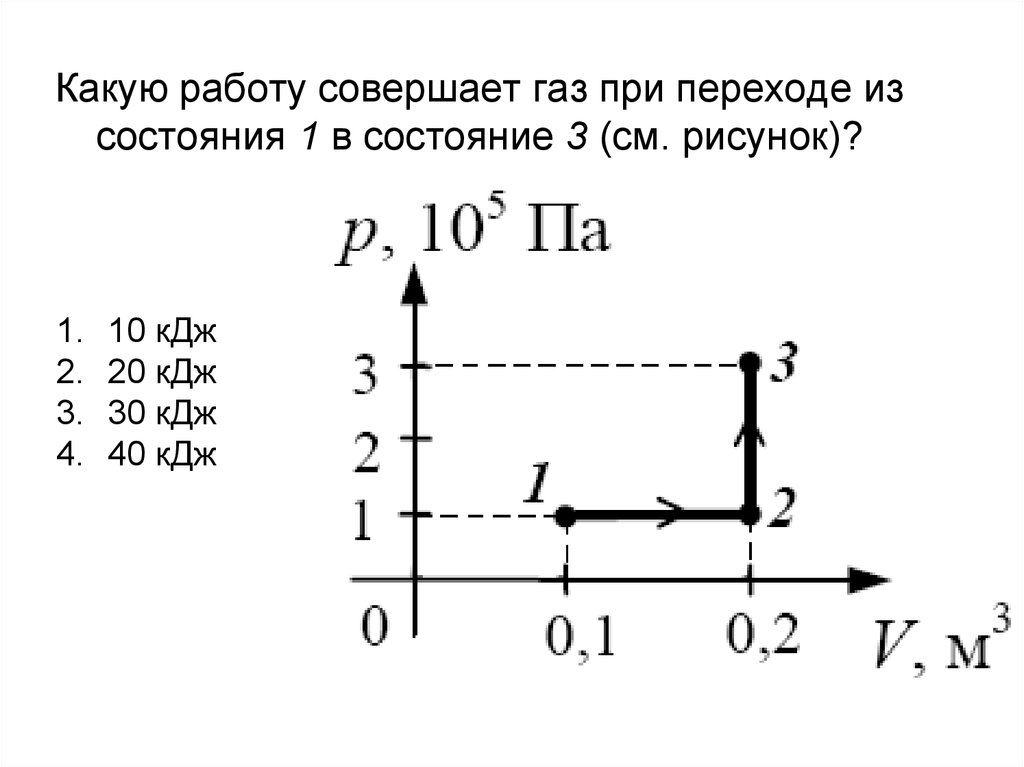 , Дуг Дэвис; все права защищены
, Дуг Дэвис; все права защищены
Закон идеального газа
Термодинамика , которая началась как попытка повысить эффективность паровых двигателей в начале 1800-х годов, может рассматриваться как исследование взаимосвязи между теплом, передаваемым к объекту или от него, и работой, выполняемой над объектом или объектом. . И теплота, и работа связаны с передачей энергии, но теплота связана с передачей энергии из-за разницы температур.
нулевой закон термодинамики (не обвиняйте меня, я его не назвал!) утверждает, что если объект А находится в тепловом равновесии с объектом В, а объект В находится в тепловом равновесии с объектом С, то объекты А и С должны находиться в тепловом равновесии друг с другом. Этот закон настолько интуитивен, что его почти не нужно формулировать, но, определяя доказательства 1-го и 2-го законов термодинамики, ученые поняли, что им нужно конкретно сформулировать этот закон, чтобы завершить свои доказательства.
первый закон термодинамики на самом деле является переформулировкой закона сохранения энергии. В частности, в нем утверждается, что изменение внутренней энергии замкнутой системы равно количеству теплоты, переданной системе, плюс работа, совершенная над системой, и записывается как:
В этом уравнении важно отметить соглашения о знаках, где положительное значение теплоты, Q, представляет собой тепло, добавленное в систему, а положительное значение работы, W, указывает на работу, выполненную над газом. Если бы энергия вытягивалась из системы, как в случае теплоты, отбираемой из системы, или работы, совершаемой системой, эти величины были бы отрицательными.
В большинстве случаев вы будете использовать первый закон термодинамики для анализа поведения идеальных газов, который можно упростить, проанализировав определение работы над газом.
Если работа — это сила, умноженная на перемещение, а давление — это сила, действующая на площадь, то силу можно заменить давлением, умноженным на площадь. Площадь, умноженная на смещение, дает изменение объема газа. Из-за соглашения о знаках, согласно которому работа, совершаемая над газом, положительна (соответствует уменьшению объема), вы можете записать работу как W = -PΔV.
Площадь, умноженная на смещение, дает изменение объема газа. Из-за соглашения о знаках, согласно которому работа, совершаемая над газом, положительна (соответствует уменьшению объема), вы можете записать работу как W = -PΔV.
Вопрос: Пять тысяч джоулей тепла добавляется в замкнутую систему, которая затем выполняет работу в 3000 джоулей. Каково чистое изменение внутренней энергии системы?
Ответ:
Вопрос: Жидкость превращается в газ при атмосферном давлении (101 325 Па). Объем жидкости составил 5×10 -6 м 9 .0078 3 . Объем газа 5×10 -3 м 3 . Сколько работы было проделано в процессе?
Ответ:
Диаграммы давление-объем (диаграммы PV) являются полезными инструментами для визуализации термодинамических процессов газов. Эти диаграммы показывают давление по оси ординат и объем по оси абсцисс и используются для описания изменений, которые претерпевает заданное количество газа. Поскольку количество газа остается постоянным, диаграмма PV не только показывает давление и объем, но также может использоваться для определения температуры газа в сочетании с законом идеального газа. Пример диаграммы PV показан ниже, показывая два состояния газа, состояние A и состояние B.
Эти диаграммы показывают давление по оси ординат и объем по оси абсцисс и используются для описания изменений, которые претерпевает заданное количество газа. Поскольку количество газа остается постоянным, диаграмма PV не только показывает давление и объем, но также может использоваться для определения температуры газа в сочетании с законом идеального газа. Пример диаграммы PV показан ниже, показывая два состояния газа, состояние A и состояние B.
При переходе из состояния А в состояние В объем газа увеличивается, а давление газа уменьшается. При переходе из состояния В в состояние А объем газа уменьшается, а давление увеличивается. Поскольку работа, проделанная над газом, определяется как W=-PΔV, вы можете найти работу, проделанную над газом, графически из диаграммы PV, взяв площадь под кривой. Из-за соглашения о положительных/отрицательных знаках, когда объем газа расширяется, газ совершает работу (W отрицательное значение), а когда газ сжимается, над газом совершается работа (W положительное значение).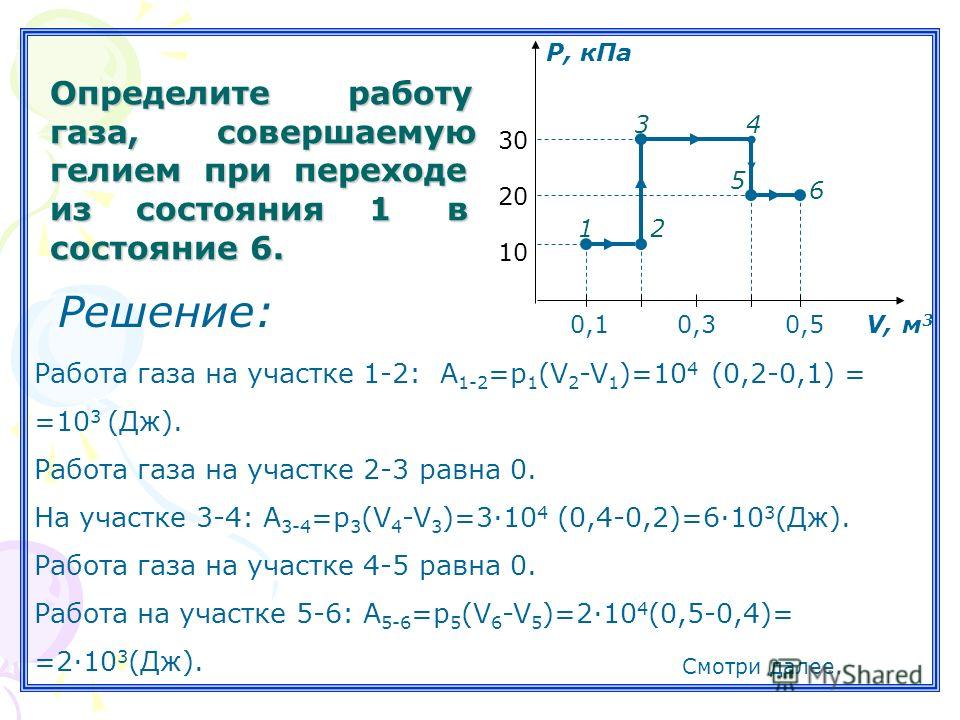
Вопрос: Используя диаграмму PV справа, найдите объем работы, необходимый для перехода из состояния A в состояние B, а затем объем работы, необходимый для перехода из состояния B в состояние C.
Ответ: Объем работы при переходе из состояния A в B равен площади под графиком для этого перехода. Так как под прямой нет площади, то работа не совершалась. Работу при переходе из состояния В в состояние С можно найти, взяв площадь под линией на PV-диаграмме.
Обратите внимание, что работа отрицательна, что указывает на то, что газ совершил работу, что коррелирует с расширением газа.
При изучении изменений состояния идеального газа существует ряд изменений состояния, при которых одна из характеристик газа или процесса остается постоянной, что показано на диаграмме PV ниже.
Типы процессов включают:
- Адиабатический — Теплота (Q) не передается в систему или из нее
- Изобарический — Давление (P) остается постоянным
- Изохорный — Объем (V) остается постоянным
- Изотермический — Температура (T) остается постоянной
В адиабатическом процессе тепловой поток (Q) равен нулю. Применяя первый закон термодинамики, если ΔU=Q+W, а Q равно 0, изменение внутренней энергии газа должно быть равно работе, совершенной над газом (ΔU=W).
Применяя первый закон термодинамики, если ΔU=Q+W, а Q равно 0, изменение внутренней энергии газа должно быть равно работе, совершенной над газом (ΔU=W).
В изобарическом процессе давление газа остается постоянным. Поскольку давление постоянно, на диаграмме PV для изобарического процесса показана горизонтальная линия. Далее, применив это к закону идеального газа, вы обнаружите, что V/T должно оставаться постоянным для процесса.
В изохорном процессе объем газа остается постоянным. Диаграмма PV для изохорного процесса представляет собой вертикальную линию. Поскольку W=-PΔV, а ΔV=0, работа над газом равна нулю. Это также отражено графически на диаграмме PV. Работу можно найти, взяв площадь под графиком PV, но площадь под вертикальной линией равна нулю. Применяя это к закону идеального газа, вы обнаружите, что P/T должно оставаться постоянным для изохорного процесса.
В изотермическом процессе температура газа остается постоянной. Поэтому линии на PV-диаграмме, описывающие любой процесс, происходящий при постоянной температуре, называются изотермами. В изотермическом процессе произведение давления на объем газа остается постоянным. Далее, поскольку температура постоянна, внутренняя энергия газа должна оставаться постоянной.
Поэтому линии на PV-диаграмме, описывающие любой процесс, происходящий при постоянной температуре, называются изотермами. В изотермическом процессе произведение давления на объем газа остается постоянным. Далее, поскольку температура постоянна, внутренняя энергия газа должна оставаться постоянной.
Вопрос: Идеальный газ совершает адиабатическое расширение, совершая работу в 2000 Дж. На сколько изменилась внутренняя энергия газа?
Ответ: Поскольку процесс адиабатический, Q=0, следовательно:
Вопрос: Теплота отводится от идеального газа при падении его давления с 200 кПа до 100 кПа. Затем газ расширяется с объема 0,05 м 3 до 0,1 м 3 , как показано на диаграмме PV ниже. Если кривая АС представляет собой изотерму, найти работу, совершенную газом, и теплоту, переданную газу.
Ответ: Работа, совершаемая газом при перемещении из А в В, равна нулю, так как площадь под графиком равна нулю. Однако при движении из В в С работу, совершаемую газом, можно найти, взяв площадь под графиком.
Знак минус указывает на то, что газ совершил работу в 5000 джоулей. Поскольку АС находится на изотерме, температура газа должна оставаться постоянной, поэтому внутренняя энергия газа должна оставаться постоянной. Зная, что ΔU=Q+W, если ΔU=0, то Q должно быть равно -W, следовательно, к газу должно быть добавлено 5000 джоулей.
Второй закон термодинамики s можно сформулировать различными способами. В одном из утверждений этого закона говорится, что тепло естественным образом перетекает от более теплого объекта к более холодному и не может течь от более холодного объекта к более теплому без совершения работы над системой. Это можно довольно легко наблюдать в повседневных обстоятельствах. Например, контакт холодной ложки с горячим супом никогда не приведет к тому, что суп станет горячее, а ложка — холоднее.
Например, контакт холодной ложки с горячим супом никогда не приведет к тому, что суп станет горячее, а ложка — холоднее.
Второй закон термодинамики также ограничивает эффективность любой тепловой машины и доказывает, что невозможно создать тепловую машину со 100-процентным КПД, даже если полностью устранить трение.
Другая формулировка этого закона гласит, что уровень энтропии , или беспорядка, в замкнутой системе может только возрастать или оставаться прежним. Это означает, что ваш рабочий стол никогда не станет более организованным без работы. Это также означает, что вы не можете бросить горсть пластиковых строительных блоков и наблюдать, как они самопроизвольно приземляются на впечатляющую модель средневекового замка. К сожалению, это даже означает, что независимо от того, сколько раз Шалтай-Болтай падает со стены, все его фигуры на земле никогда не окажутся более организованными после того, как он упадет на землю, по сравнению с тем, как он потерял равновесие.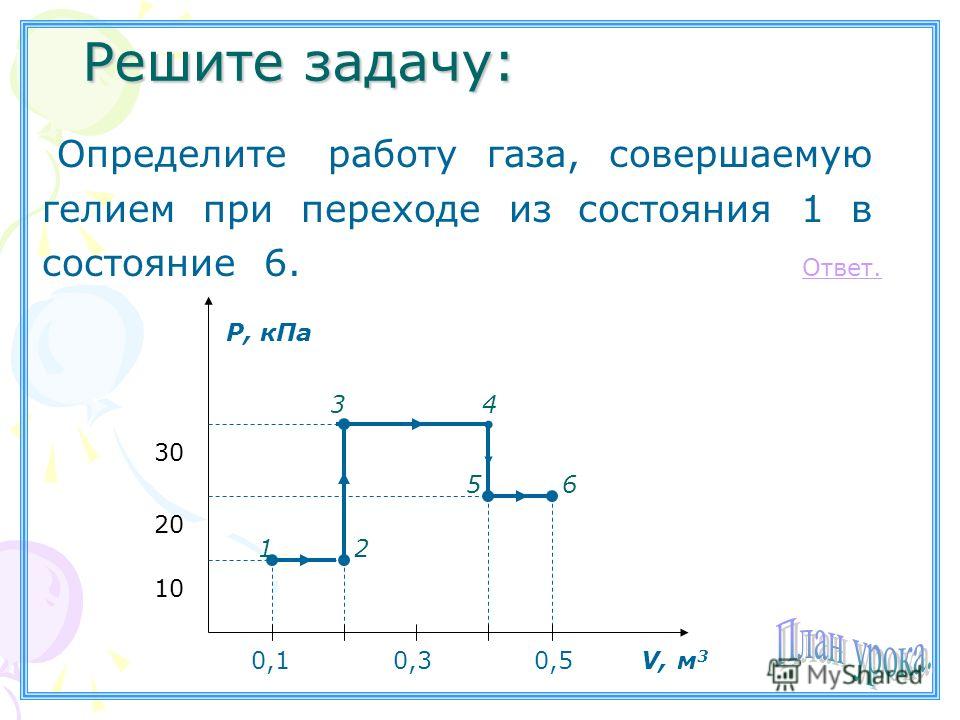

 Это означает, что мы можем использовать закон идеального газа как
Это означает, что мы можем использовать закон идеального газа как
 3 При постоянном давлении 1,5 атм газ
3 При постоянном давлении 1,5 атм газ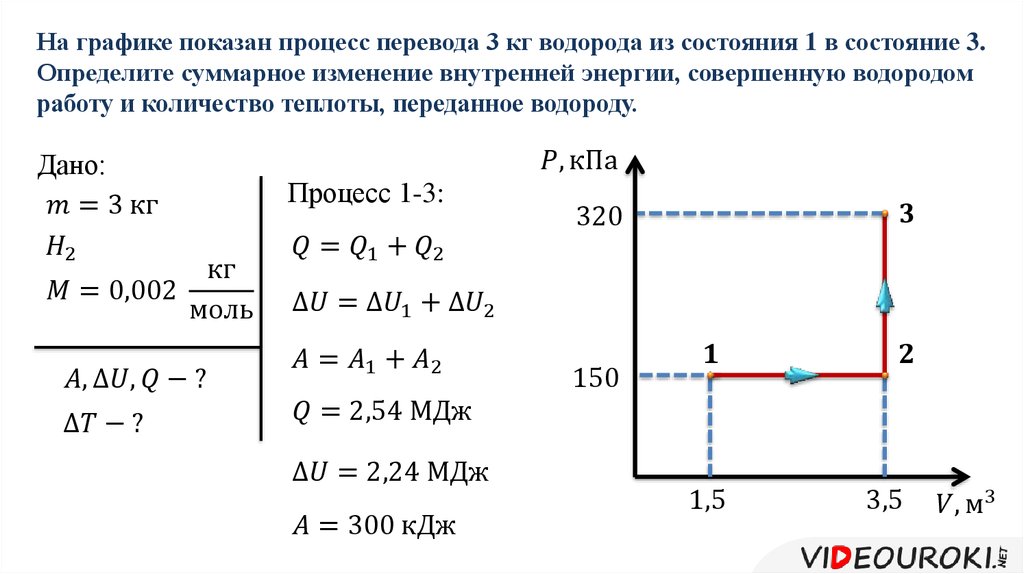 Это означает, что его чистое изменение внутренней энергии равно
Это означает, что его чистое изменение внутренней энергии равно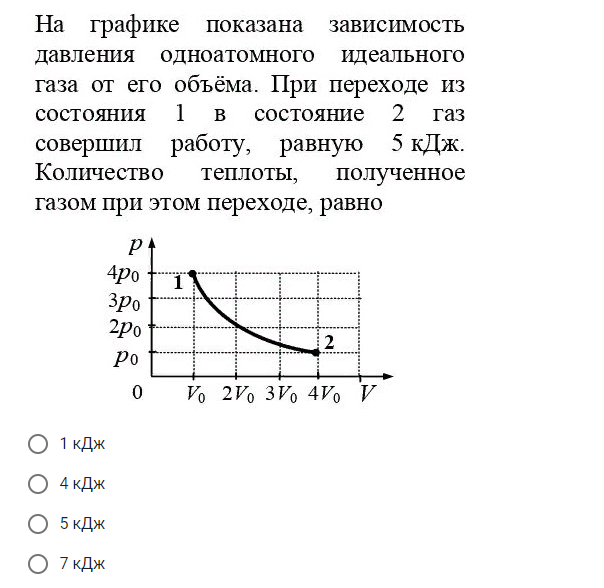
 Мы могли бы также назвать это V 1 ,
Мы могли бы также назвать это V 1 ,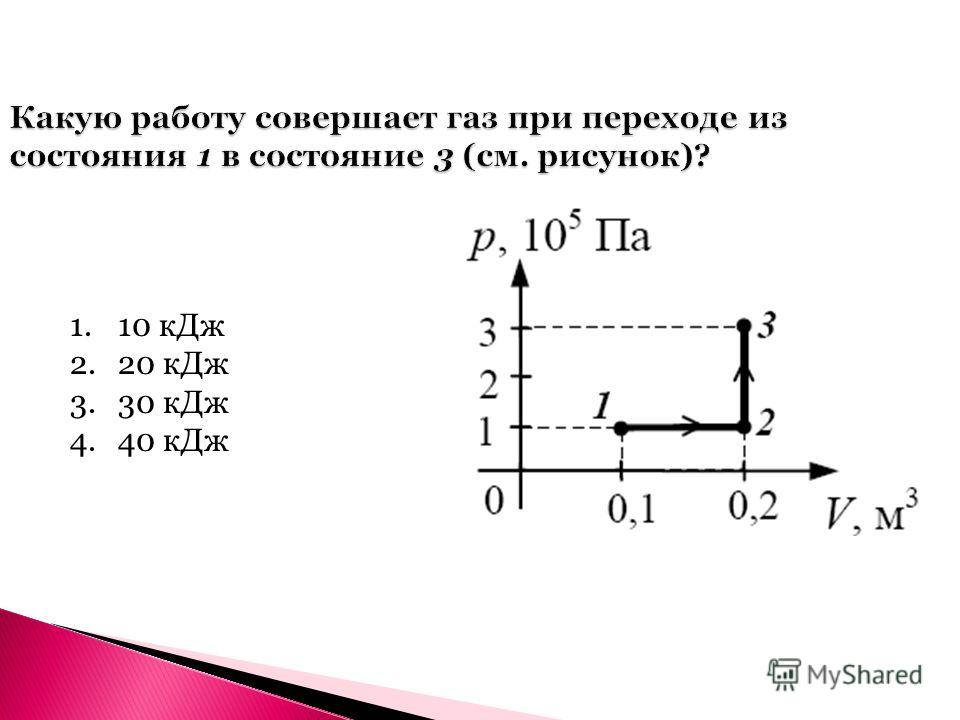
 7 Двигатель Карно работает с горячим баком 650°C
7 Двигатель Карно работает с горячим баком 650°C 8 КПД бензинового двигателя 0,55. Оценить температуру
8 КПД бензинового двигателя 0,55. Оценить температуру