Содержание
Линейная скорость через угловую, теория и онлайн калькуляторы
Линейная скорость через угловую, теория и онлайн калькуляторы
Определение
Мгновенной (истинной) скоростью ($\overline{v}$) называют векторную физическую величину, равную производной от вектора перемещения по времени ($t$):
\[\overline{v}={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta \overline{r}}{\Delta t}=\frac{d\overline{r}}{dt}\ }\left(1\right).\]
$\Delta \overline{r}$- вектор перемещения материальной точки, это перемещение точка совершает за отрезок времени $\Delta t$.
Выражение линейной скорости через угловую скорость
Скорость называют мгновенной, так как ее значение показывает величину скорости в определенный момент времени.
Так как вектор перемещения $\Delta \overline{r}$ направлен по хорде, которая соединяет две близкие точки криволинейной траектории движения частицы, при уменьшении расстояния между этими точками, вектор $\Delta \overline{r}$ занимает положение касательной к линии, по которой движется частица. Из определения (1) следует, что мгновенная скорость направлена по касательной к траектории движения.
Из определения (1) следует, что мгновенная скорость направлена по касательной к траектории движения.
Скорость прохождения пути ($s$) определяют:
\[v={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta s}{\Delta t}=\frac{ds}{dt}\left(2\right).\ }\]
Мгновенную скорость называют линейной тогда, когда хотят подчеркнуть ее отличие от угловой скорости.
Если материальная точка движется по окружности, то ее положение характеризуют при помощи угла поворота ($\varphi $), который образует радиус-вектор ($\overline{r}$), определяющий положение рассматриваемой точки А с выделенным неизменным направлением от которого производят отсчет (рис.1).
Быстроту изменения угла поворота $\varphi $ характеризуют при помощи такой физической величины как угловая скорость. Обычно угловую скорость обозначают буквой $\omega $. Угловая скорость равна:
\[\omega =\frac{d\varphi }{dt}\left(3\right).\]
Вращение называют равномерным, если угловая скорость постоянна $\omega =const$. При равномерном вращении $\omega $ можно называть угловой частотой.
При равномерном вращении $\omega $ можно называть угловой частотой.
Линейная скорость движения точки по окружности связана с угловой скоростью. Пусть точка проходит путь равный длине дуги XA (рис.1). Этот путь обозначим $s$. Если радиус окружности равен$\ R=const$, то длину дуги найдем как:
\[s=R\varphi \ \left(4\right).\]
Продифференцируем обе части выражения (4) по времени, имеем:
\[\frac{ds}{dt}=\frac{d\left(R\varphi \right)}{dt}=R\frac{d\varphi }{dt}\left(5\right).\]
Мы видим, что в левой части получена величина линейной скорости, в правой части радиус окружности умножен на угловую скорость:
\[v=R\omega \left(6\right).\]
Формула (6) будет справедлива при движении точки по криволинейной траектории отличной от окружности, но в этом случае $R$ — радиус кривизны траектории в месте нахождения частицы.
В векторном виде выражение (6) записывают так:
\[\overline{v}=\overline{\omega }\times \overline{r}\left(7\right),\]
$\overline{r}$ — вектор, соединяющий ось вращения и движущуюся точку (рис. 2). Модуль скорости, используя формулу (7) найдем как:
2). Модуль скорости, используя формулу (7) найдем как:
\[v=\omega r{\sin \alpha \ \left(8\right),\ }\]
где $\alpha $ — угол между вектором угловой скорости и $\overline{r}.$
Угловая скорость через линейную
Исходя из приведенных выше формул угловую скорость можно выразить через линейную. При движении по окружности:
\[\omega =\frac{v}{R}\left(9\right).\]
Или используя формулу (8) угловую скорость выразим как:
\[\omega =\frac{v}{r{\sin \alpha \ }}\left(10\right).\]
Примеры задач с решением
Пример 1
Задание. Диск равномерно вращается вокруг оси (O), перпендикулярной его плоскости, проходящей через его центр (рис.3). Линейная скорость точки A равна $v_1$, Точка B находится на расстоянии $\Delta l$ ближе к оси и имеет лилейную скорость $v_2$. Какова угловая скорость вращения диска ($\omega $)?
Решение.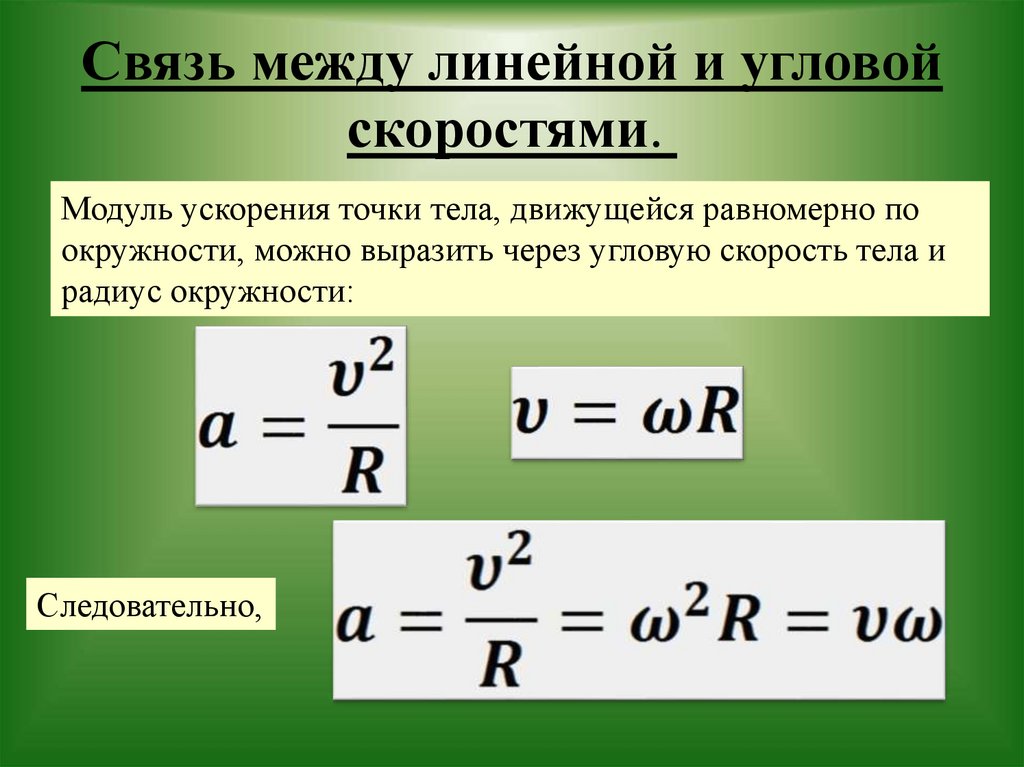 Основой для решения задачи будет формула:
Основой для решения задачи будет формула:
\[\omega =\frac{v}{R}\left(1.1\right).\]
Угловые скорости движения точки A и B одинаковы (${\omega }_A={\omega }_B$), запишем выражение для каждой из этих скоростей используя (1.1):
\[{\omega }_A=\frac{v_1}{R_1};;\ {\omega }_B=\frac{v_2}{R_2}\left(1.2\right).\]
$R_1$ — расстояние от точки O до точки A; $R_2=R_1-\Delta l$ — расстояние от точки B до точки O. Приравняем правые части выражений (1.2), выразим расстояние $R_1$:
\[\frac{v_1}{R_1}=\frac{v_2}{R_1-\Delta l}\to R_1=\frac{\Delta l\cdot v_1}{v_1-v_2}\left(1.3\right).\]
Найдем угловую скорость точки A:
\[{\omega }_A=v_1\cdot \frac{v_1-v_2}{\Delta l\cdot v_1}=\frac{v_1-v_2}{\Delta l}.\]
Ответ. Угловая скорость всех точек диска равна $\omega =\frac{v_1-v_2}{\Delta l}$
Пример 2
Задание. 2=15\ \left(\frac{м}{с}\right).\]
2=15\ \left(\frac{м}{с}\right).\]
Ответ. $v\left(t’\right)=15\frac{м}{с}$
Читать дальше: масса и плотность вещества.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Как рассчитывается линейная скорость?
Оглавление
Время чтения:
4 минуты
670
Интуитивное понятие о скорости мы получаем ещё с детства. Например, глядя в окно или находясь на улице отмечаем про себя, что некоторые из людей идут быстрее, чем другие, а машины на проезжей части движутся быстрее, чем любой из пешеходов. Однако для физики, как науки, такого, бытового понимания о скорости недостаточно, поэтому вводится её точное определение.
Понятие скорости
Скоростью материальной точки (тела) при равномерном движении называется физическая величина, показывающая, какой путь точка (тело), проходит за единицу времени.
Подчеркнём, что речь идёт именно о пути, а не о перемещении. Перемещением называется вектор, соединяющий точку начала и точку конца движения. Его величина равна расстоянию между этими точками. Путь представляет собой длину траектории, по которой происходило движение. Наглядно это можно показать на рисунке.
Рис.1 Красная стрелка – перемещение. Коричневая кривая – путь.
Равномерным движением называют движение, при котором за одинаковые промежутки времени тело проходит одно и то же расстояние. Направление движения при этом может изменяться. В качестве примера можно привести равномерное перемещение точки по окружности.
Формула понятия скорости следующая:
\[\overline{\mathrm{v}}=s / t\]
Чёрточка над \[\overline{\mathrm{v}}\] свидетельство того, что скорость является векторной, т.е. имеющей направление, величиной. Путь s и время t являются скалярными величинами, такими, которые направления в пространстве не имеют.
Чёрточка над \[\overline{\mathrm{v}}\] свидетельство того, что скорость является векторной, т. е. имеющей направление, величиной. Путь s и время t являются скалярными величинами, такими, которые направления в пространстве не имеют.
е. имеющей направление, величиной. Путь s и время t являются скалярными величинами, такими, которые направления в пространстве не имеют.
Из приведённой формулы очень легко найти размерность скорости. Т. к. расстояние измеряется в метрах, а время в секундах, то единицей скорости будет метр в секунду м/с. Отметим, что на практике часто скорость измеряют не в метрах в секунду, а, например, в километрах в час.
Существует ещё так называемая средняя скорость – скалярная величина, равная скорости, с которой бы тело перемещалось, если бы преодолевало путь, двигаясь равномерно.
Примеры
Поезд длиной 300 метров, двигаясь равномерно, проезжает тоннель длиной 420 метров за 3 минуты. Найти скорость поезда.
Решение:
Длину поезда обозначим через l, а длину тоннеля через L.
Словосочетание «проезжает тоннель за 3 минуты» означает, что это время поезд входит в тоннель кабиной машиниста и выходит с концом последнего вагона. Пройденное им расстояние S в таком случае является суммой длины тоннеля и длины поезда.
Пройденное им расстояние S в таком случае является суммой длины тоннеля и длины поезда.
\[S = I + L = 300 + 420 = 720 м/с.\]
Скорость поезда – это скорость любой из его точек. Для простоты будем считать, что это скорость кабины машиниста.
Переводим минуты в секунды: 3 * 60 = 180с.
Скорость получаем, разделив перемещение на время: 720/180 = 4 м/с.
Ответ: Скорость поезда равна 4 м/с.
Машина 3 часа едет со скоростью 4 км/ч, затем 4 часа со скоростью 61,2 км/ч. Требуется найти среднюю скорость движения машины на всем её пути.
Решение:
Обозначим время движения машины со скоростью 4 км/ч, как \[t_{1}\], а время движения машины со скоростью 61,2 км/ч, как \[t_{2}\].
Находим общий путь, который проехала машина. Обозначим его, как S. Общий равен сумме путей, которые ехала машина со скоростью 58,4 км/ч и 61,2 км/ч. Первый из них обозначим как \[S_{1}\], он равен \[S_{1}\] = 3*58,4 = 175,2 км
Второй из них обозначим как S2, он равен: \[S_{2} = 4*61,2 = 244,8 км\]
Складываем эти расстояния и получаем: S = 175,2 + 244,8 = 420 км
Это есть весь путь, пройденный нашей машиной.
Общее время t, которое она потратила будет \[t = t_{1} + t_{2} =3 + 4 = 7 ч\]
Чтобы узнать среднюю скорость, делим общее расстояние на общее время v = S/t = 420/7 = 60 км/ч.
Ответ: Средняя скорость машины равна 60 км/ч.
Обращать время в секунды, а скорость в метры в секунду здесь смысла не имеет, можно и так получить нужное решение.
Линейная скорость
Линейной скоростью именуют величину равную пути, проходимым телом за единицу времени. Движение тела при этом может быть как прямолинейным так и совершаться по криволинейной траектории, например, окружности. Отметим, что линейная скорость всегда направлена по касательной к траектории.
Формул для расчета линейной скорости существует множество, но общей можно назвать:
\[v=S / t\]
S – путь, который прошло тело, t – время, которое оно на это потратило.
Если тело вращается по окружности, то путь, проходимый им, равен её длине. Как известно из геометрии, указанная величина равна 2πR, где R – радиус окружности. Отсюда легко сообразить, что линейная скорость тела при равномерном движении по окружности будет \[\boldsymbol{v=2 \pi R / T}\].
Как известно из геометрии, указанная величина равна 2πR, где R – радиус окружности. Отсюда легко сообразить, что линейная скорость тела при равномерном движении по окружности будет \[\boldsymbol{v=2 \pi R / T}\].
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
О связи между линейной и угловой скоростями
Угловой скоростью называется векторная величина, показывающая, насколько быстро и в каком направлении вращается материальная точка или тело относительно центра вращения.
Угловая скорость
Обозначается она буквой ω. Формула нахождения угловой скорости следующая:
\[\overline{\omega}=\phi / t\],
где ϕ – угловое перемещение, t – время.
Измеряется угловая скорость в радианах в секунду рад/с.
Теперь о связи между линейной и угловой скоростью. Из формулы\[\boldsymbol{v=2 \pi R / T}\] следует, что v также будет равно v = 2πRν, где ν – частота вращения точки. {2} R\]
{2} R\]
Оценить статью (39 оценок):
Поделиться
1.4: Скорость и угловая скорость
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 7100
- Тед Сандстром и Стивен Шликер
- Государственный университет Гранд-Вэлли через ScholarWorks @Grand Valley Государственный Университет
Основные вопросы
Следующие вопросы предназначены для того, чтобы направлять наше изучение материала в этом разделе. Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.
- Что такое длина дуги?
- В чем разница между линейной скоростью и угловой скоростью?
- Какие формулы связывают линейную скорость с угловой скоростью?
Начальное занятие
- Какова формула длины окружности \(C\) круга, радиус которого равен \(r\)?
- Предположим, что человек \(A\) идет по окружности круга радиусом 10 футов, а человек B идет по окружности круга радиусом 20 футов.
 Кроме того, предположим, что обоим \(A\) и \(B\) требуется 1 минута, чтобы пройти четверть окружности их соответствующих кругов (четверть полного оборота). Кто прошел наибольшее расстояние?
Кроме того, предположим, что обоим \(A\) и \(B\) требуется 1 минута, чтобы пройти четверть окружности их соответствующих кругов (четверть полного оборота). Кто прошел наибольшее расстояние? - Предположим, что оба человека продолжают идти с той же скоростью, что и в первую минуту. Сколько полных оборотов по кругу совершит каждый человек за 8 минут? Через 10 минут?
Длина дуги на окружности
В разделе 1.3 мы узнали, что мера угла в радианах равна длине дуги на единичной окружности, связанной с этим углом. Таким образом, дуга длины 1 на единичной окружности образует угол в 1 радиан. Будут времена, когда также будет полезно знать длину дуг на других окружностях, которые опираются на тот же самый угол.
Рисунок \(\PageIndex{1}\): Дуги, опирающиеся на угол в 1 радиан.
На рисунке \(\PageIndex{1}\) внутренний круг имеет радиус 1, внешний круг имеет радиус \(r\), а показанный угол имеет меру \(\theta\ ) радианы. Таким образом, длина дуги на единичной окружности, опирающейся на угол, равна \(\theta\), и мы использовали s для представления длины дуги на окружности радиуса \(r\), опирающейся на угол.
Таким образом, длина дуги на единичной окружности, опирающейся на угол, равна \(\theta\), и мы использовали s для представления длины дуги на окружности радиуса \(r\), опирающейся на угол.
Напомним, что длина окружности радиуса \(r\) равна \(2\pi r\), а длина окружности радиуса 1 равна \(2\pi\). Следовательно, отношение длины дуги \(s\) на окружности радиуса \(r\), которая образует угол \(\тета\) радиан, к соответствующей дуге на единичной окружности, равно \(\dfrac{2 \pi r}{2\pi} = r\). Отсюда следует, что
\[\dfrac{s}{\theta} = \dfrac{2\pi r}{\pi}\]
\[s = r\theta\]
Определение
На окружности радиуса \ (r\), длина дуги s, пересекаемая центральным углом в радианах, равна
\[s = r\theta\]
Примечание
Важно помнить, что для вычисления длины дуги мы должны измерить центральную угол в радианах.
(Непонятно, почему буква \(s\) обычно используется для обозначения длины дуги. Одно из объяснений состоит в том, что дуга «стягивает» угол. )
)
Упражнение \(\PageIndex{1}\)
Использование окружностей в начальном упражнении для этого раздела:
- Используйте формулу для длины дуги, чтобы определить длину дуги на окружности радиусом 10 футов, которая тянется центральный угол \(\dfrac{\pi}{2}\) радиан. Результат равен одной четверти длины окружности?
- Используйте формулу для длины дуги, чтобы определить длину дуги на окружности радиусом 20 футов, образующей центральный угол \(\dfrac{\pi}{2}\) радиан. Результат равен одной четверти длины окружности? 9\circ}) = \dfrac{11\pi}{90}\), и \[s = r\theta = (3ft)\dfrac{11\pi}{90}\] \[s = \dfrac{11 \pi}{30}\] Длина дуги составляет \(\dfrac{11\pi}{30}\) футов или около \(1,1519\) футов.
Почему радианы?
Градусная мера привычна и удобна, так почему же мы вводим единицу измерения радиан? Это хороший вопрос, но с тонким ответом. Как мы только что видели, длина \(s\) дуги на окружности радиуса \(r\), опирающейся на угол \(\theta\) радиан, определяется выражением \(s = r\theta\), поэтому \(\тета = \dfrac{s}{r}\). В результате радиан представляет собой отношение двух длин (отношение длины дуги к радиусу окружности), что делает радиан безразмерной величиной. Таким образом, измерение в радианах можно рассматривать как действительное число. Это удобно для работы с длиной дуги (и угловой скоростью, как мы скоро увидим), а также будет полезно при изучении периодических явлений в главе 2. По этой причине радианная мера повсеместно используется в математике, физике и технике как в отличие от степеней, потому что, когда мы используем градусную меру, мы всегда должны учитывать градусную размерность в вычислениях. Это означает, что мера в радианах на самом деле более естественна с математической точки зрения, чем градусная мера.
В результате радиан представляет собой отношение двух длин (отношение длины дуги к радиусу окружности), что делает радиан безразмерной величиной. Таким образом, измерение в радианах можно рассматривать как действительное число. Это удобно для работы с длиной дуги (и угловой скоростью, как мы скоро увидим), а также будет полезно при изучении периодических явлений в главе 2. По этой причине радианная мера повсеместно используется в математике, физике и технике как в отличие от степеней, потому что, когда мы используем градусную меру, мы всегда должны учитывать градусную размерность в вычислениях. Это означает, что мера в радианах на самом деле более естественна с математической точки зрения, чем градусная мера.
Линейная и угловая скорость
Связь между дугой на окружности и углом, который она образует, измеряемым в радианах, позволяет нам определять величины, связанные с движением по окружности. Объекты, движущиеся по круговым траекториям, обладают двумя типами скорости: линейной и угловой скоростью. Подумайте о вращении на карусели. Если вы уроните камешек с края движущейся карусели, камешек не упадет прямо вниз. Вместо этого он будет продолжать двигаться вперед со скоростью, которую карусель имела в момент выпуска камешка. Это линейная скорость камня. линейная скорость измеряет, как длина дуги изменяется во времени.
Подумайте о вращении на карусели. Если вы уроните камешек с края движущейся карусели, камешек не упадет прямо вниз. Вместо этого он будет продолжать двигаться вперед со скоростью, которую карусель имела в момент выпуска камешка. Это линейная скорость камня. линейная скорость измеряет, как длина дуги изменяется во времени.
Рассмотрим точку \(P\), движущуюся с постоянной скоростью по окружности радиуса \(r\). Это называется равномерным круговым движением . Предположим, что P перемещается на расстояние s единиц за время \(t\). Линейная скорость v точки \(P\) равна пройденному ею расстоянию, деленному на прошедшее время. То есть \(v = \dfrac{s}{t}\). Расстояние s — это длина дуги, и мы знаем, что \(s = r\theta\).
Определение: линейная скорость
Рассмотрим точку \(P\), движущуюся с постоянной скоростью по окружности радиуса \(r\). линейная скорость \(v\) точки \(P\) определяется выражением
\[v = \dfrac{s}{t} = \dfrac{r\theta}{t}\]
где \(\theta\), измеренный в радианах, представляет собой центральный угол, опирающийся на дугу длины \(s\).
Другой способ измерения скорости движения объекта с постоянной скоростью по круговой траектории называется угловой скоростью. В то время как линейная скорость измеряет, как длина дуги изменяется с течением времени, угловая скорость является мерой того, насколько быстро изменяется центральный угол с течением времени.
Определение: угловая скорость
Рассмотрим точку P, движущуюся с постоянной скоростью по окружности радиуса r по дуге, соответствующей центральному углу измерения \(\theta\) (в радианах). Угловая скорость \(\omega\) точки равна отношению угла \(\theta\) в радианах к времени t, которое требуется, чтобы выметать этот угол. Это
\[\omega = \dfrac{\theta}{t}.\]
Примечание
Символ \(\omega\) — это строчная греческая буква «омега». Также обратите внимание, что угловая скорость не зависит от радиуса r.
Это несколько специальное определение угловой скорости, которое немного отличается от общего термина, используемого для описания скорости вращения точки по окружности.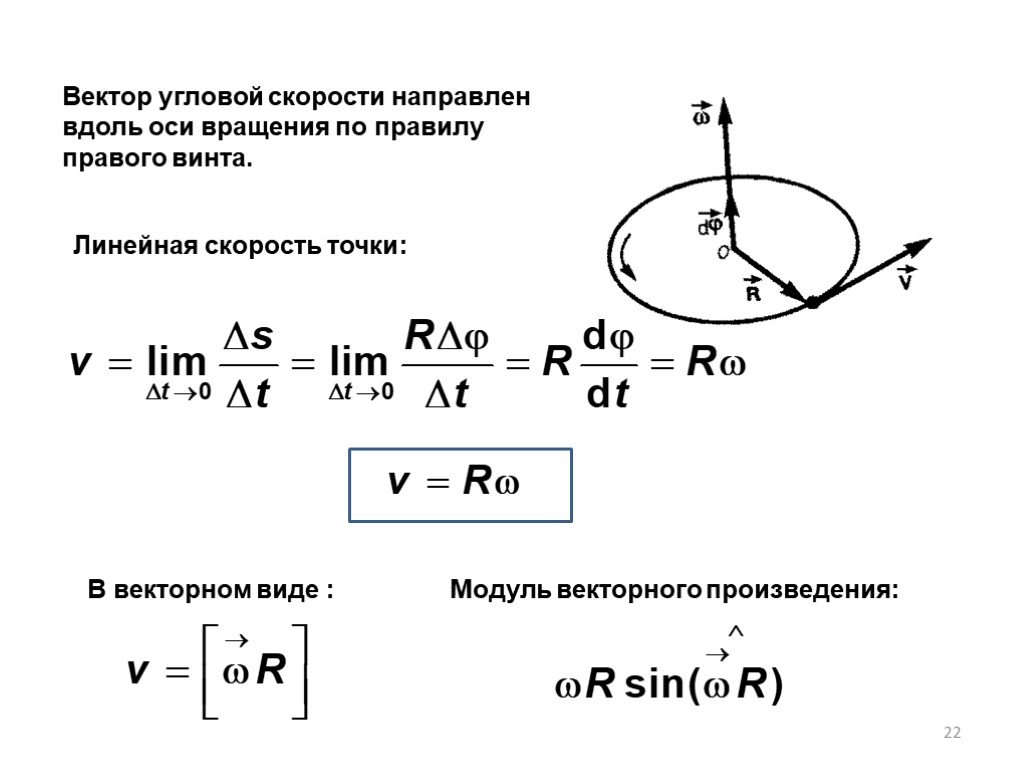 Этот термин равен оборотов в минуту или оборотов в минуту . Иногда используется единица оборотов в секунду . Лучший способ представить число оборотов в минуту — использовать «долю единицы измерения» \(\dfrac{rev}{min}\). Поскольку 1 оборот равен \(2\pi\) радианам, мы видим, что если объект min движется со скоростью x оборотов в минуту, то
Этот термин равен оборотов в минуту или оборотов в минуту . Иногда используется единица оборотов в секунду . Лучший способ представить число оборотов в минуту — использовать «долю единицы измерения» \(\dfrac{rev}{min}\). Поскольку 1 оборот равен \(2\pi\) радианам, мы видим, что если объект min движется со скоростью x оборотов в минуту, то
\[\omega = x \dfrac{об} {мин} \cdot \dfrac{2\pi рад} {об} = x(2\pi)\dfrac {рад}{мин}.\]
Упражнение \(\PageIndex{2}\)
Предположим, что круглый диск вращается со скоростью 40 оборотов в минуту. Мы хотим определить линейную скорость v (в футах в секунду) точки, которая находится в 3 футах от центра диска.
- Определите угловую скорость \(\omega\) точки в радианах в минуту. Подсказка : Используйте формулу \[\omega = x \dfrac{об} {мин} \cdot \dfrac{2\pi rad}{об}.\]
- Теперь мы знаем \(\omega = \dfrac{\theta}{t}\). Поэтому используйте формулу \(v = \dfrac{r\theta}{t}\), чтобы определить \(v\) в футах в минуту.

- Наконец, преобразуйте линейную скорость v в футах в минуту в футы в секунду.
- Ответить
1. Мы видим, что
\[\omega = 40\dfrac{об} {мин} \times \dfrac{2\pi\space рад}{об}\]
\[\omega = 80\pi\dfrac{rad}{мин}\ ]2. Результат пункта (а) дает
\[v = r(\dfrac{\theta}{r}) = r\omega\]
\[v = (3ft) \times 80\pi\dfrac{rad}{min}\]
\[v = 240\pi\dfrac{ft}{мин}\]3. Теперь мы конвертируем футы в минуту в футы в секунду.
\[v = 240\pi\dfrac{ft}{min} \times \dfrac{1\space min}{60\space sec}\]
\[v = 4\pi\dfrac{ft}{sec} \приблизительно 12,566\dfrac{ft}{sec}\]
Обратите внимание, что в упражнении 1.18, как только мы определили угловую скорость, мы смогли определить и линейную скорость. То, что мы сделали в данном конкретном случае, мы можем сделать в целом. Существует простая формула, напрямую связывающая линейную скорость с угловой скоростью. Наша формула для линейной скорости: \(v =\dfrac{s}{t} \dfrac{r\theta}{t}\). Обратите внимание, что мы можем записать это как \(v = r\dfrac{\theta}{t}\). То есть \(v = r\omega\)
Наша формула для линейной скорости: \(v =\dfrac{s}{t} \dfrac{r\theta}{t}\). Обратите внимание, что мы можем записать это как \(v = r\dfrac{\theta}{t}\). То есть \(v = r\omega\)
Примечание
Рассмотрим точку \(P\), движущуюся с постоянной (линейной) скоростью \(v\) по окружности радиуса \(r\). Если угловая скорость равна \(\omega\), то
\[v = r\omega\]
Итак, в упражнении 1.18, как только мы определили, что \(\omega = 80\pi \dfrac{rad}{min }\), мы могли бы определить v следующим образом:
\[v = r\omega = (3\space ft)(80\pi\dfrac{rad}{min} = 240\pi\dfrac{ft}{min }).\]
Обратите внимание, что, поскольку радианы «безразмерны», мы можем опускать их при работе с уравнениями, подобными предыдущему.
Пример \(\PageIndex{1}\): линейная и угловая скорость
LP (long play) или виниловая пластинка со скоростью вращения 331 об/мин представляет собой аналоговый носитель для хранения звука и долгое время использовался для прослушивания музыки. LP обычно имеет диаметр 12 или 10 дюймов. Чтобы работать с нашими формулами для линейной и угловой скорости, нам нужно знать угловую скорость в радианах в единицу времени. Для этого мы преобразуем \(33\dfrac{1}{3}\) оборотов в минуту в радианы в минуту. Мы будем использовать тот факт, что \(33\dfrac{1}{3} = \dfrac{100}{3}\)
LP обычно имеет диаметр 12 или 10 дюймов. Чтобы работать с нашими формулами для линейной и угловой скорости, нам нужно знать угловую скорость в радианах в единицу времени. Для этого мы преобразуем \(33\dfrac{1}{3}\) оборотов в минуту в радианы в минуту. Мы будем использовать тот факт, что \(33\dfrac{1}{3} = \dfrac{100}{3}\)
\[\omega = \dfrac{100}{3}\dfrac{об} {мин} \times \dfrac{2\pi \space rad}{1\space rev} = \dfrac{200\pi}{ 3}\dfrac{rad}{min}\]
Теперь мы можем использовать формулу v D r! для определения линейной скорости точки на краю 12-дюймового LP. Радиус равен 6 дюймов, поэтому
\[v = r\omega = (6\space дюймов)(\dfrac{200\pi}{3}\dfrac{rad}{min}) = 400\pi \dfrac{ дюймы}{мин}\]
Возможно, было бы удобнее выразить это как десятичное значение в дюймах в секунду. Итак, мы получаем
\[v = 400\pi \dfrac{дюймы}{мин} \times \dfrac{1\space min}{60 \space sec} \приблизительно 20,944\dfrac{дюймы}{sec}\]
Линейная скорость составляет примерно 20,944 дюйма в секунду.
Упражнение \(\PageIndex{3}\)
Для этих задач предположим, что Земля представляет собой сферу с радиусом 3959 миль. Поскольку Земля вращается вокруг своей оси, человек, стоящий на Земле, будет двигаться по кругу, перпендикулярному оси.
- Земля совершает оборот вокруг своей оси каждые \(24\) часа. Определить угловую скорость Земли в радианах в час. (Оставьте свой ответ в терминах числа ��\(\pi\).) 9\circ\) на север будет двигаться по кругу радиусом 2800 миль. Определите линейную скорость этого человека в милях в час и футах в секунду.
- Ответить
- Один оборот соответствует \(2\pi\) радианам. Итак, \[\omega = \dfrac{2\pi\space rad}{24\space hr} = \dfrac{\pi\space rad}{12\space hr}.\]
- Для определения линейной скорости используем формулу \(v = r\omega\) \[v = r\omega = (3959mi)(\dfrac{\pi}{12}\dfrac{rad}{hr}) = \dfrac{3959\pi}{12}\dfrac{mi}{hr}\] Линейная скорость составляет примерно 1036,5 миль в час.

- Для определения линейной скорости используем формулу \(v = r\omega\) \[v = r\omega = (2800mi)(\dfrac{\pi}{12}\dfrac{rad}{hr}) = \dfrac{2800\pi}{12}\dfrac{mi}{hr}\] Линейная скорость составляет примерно 733,04 мили в час. Чтобы преобразовать это в футы в секунду, мы используем тот факт, что в одной миле 5280 футов, в часе 60 минут, а в минуте 60 секунд. Итак,
\[v = (\dfrac{2800\pi}{12}\dfrac{mi}{hr})(\dfrac{5280\space ft}{1\space mi})(\dfrac{1\space hr }{60\пробел мин})(\dfrac{1\пробел мин}{60\пробел сек}) = \dfrac{(2800\pi)(5280)}{12\cdot 60\cdot 60}\dfrac{ft {сек}\]
Таким образом, линейная скорость составляет приблизительно \(1075,1\) футов в секунду.
Резюме
В этом разделе мы изучили следующие важные концепции и идеи:
- На окружности радиуса \(r\) длина дуги \(s\), пересекаемая центральным углом с мера радиана равна \[s = r\theta\]
- Равномерное круговое движение — это когда точка движется с постоянной скоростью по окружности.
 линейная скорость — это длина дуги, пройденная точкой, деленная на прошедшее время. В то время как линейная скорость измеряет, как длина дуги изменяется во времени, угловая скорость является мерой того, насколько быстро изменяется центральный угол во времени. Угловая скорость точки представляет собой меру угла в радианах, деленную на время, которое требуется, чтобы выметать этот угол.
линейная скорость — это длина дуги, пройденная точкой, деленная на прошедшее время. В то время как линейная скорость измеряет, как длина дуги изменяется во времени, угловая скорость является мерой того, насколько быстро изменяется центральный угол во времени. Угловая скорость точки представляет собой меру угла в радианах, деленную на время, которое требуется, чтобы выметать этот угол. - Для точки \(P\), движущейся с постоянной (линейной) скоростью v по окружности окружности радиуса \(r\), имеем \[v = r\omega\], где \(\omega\) есть угловая скорость точки.
Эта страница под названием 1.4: Velocity and Angular Velocity распространяется под лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Тедом Сандстромом и Стивеном Шликером (ScholarWorks @Grand Valley State University) через исходный контент. это было отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Тед Сандстром и Стивен Шликер
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 3,0
- Показать страницу TOC
- нет
- Теги
- угловая скорость
- источник@https://scholarworks.
 gvsu.edu/books/12
gvsu.edu/books/12 - скорость
Угловая скорость
Привет, Бен.
Линейная скорость — это расстояние, пройденное по прямой за единицу времени. Угловая скорость – это угол, пройденный за единицу времени.
Безусловно, проще всего это увидеть в Равномерном круговом движении. Например, камешек, застрявший в шине вашего велосипеда, движется равномерно по окружности.
Допустим, внешний диаметр шины вашего велосипеда составляет 70 см, и вы движетесь со скоростью 40 км/ч. Помните, что (игнорируя занос) шина постоянно сохраняет сцепление с дорогой, поэтому расстояние, которое вы преодолеваете, и скорость, с которой вы едете, такие же, как и скорость шины. Если мы переведем эту скорость в метры в секунду, мы получим:
Это скорость велосипеда, то есть линейная скорость велосипеда. Поскольку велосипед и шина находятся в постоянном контакте, это также линейная скорость камешка в шине.
Поскольку велосипед и шина находятся в постоянном контакте, это также линейная скорость камешка в шине.
Угловая скорость связана с углами, как следует из названия. Выражается в виде того, на какой угол поворачивается за определенное время.
Углы можно измерять разными способами: поворотами, градусами и радианами. Например, жесткий диск со скоростью 10 000 об/мин относится к его угловой скорости: 10 000 оборотов в минуту. Итак, с какой скоростью вращается наш камешек?
Этот камешек, как мы знаем, движется линейно со скоростью, эквивалентной 11,11 м/с, но он движется по окружности шины. Если внешний диаметр шины d равен 70 см, то длина окружности равна πd , что составляет около 2,199 м.
Если мы разделим линейную скорость на окружность шины, мы узнаем, сколько оборотов в секунду эта шина (и, следовательно, камешек) движется под углом:
, где R = обороты.
Это угловая скорость: на сколько поворачивает в единицу времени. Если вы хотите преобразовать это в градусы, вы просто умножаете на количество градусов на оборот (360), если вы хотите вместо этого использовать радианы, умножьте на 2π радиан на оборот.
Теперь попробуем в другом направлении. Допустим, вы знаете угловую скорость и пытаетесь вычислить соответствующую линейную скорость. Подсказка: это довольно быстро!
Возьмем в качестве примера вращение Земли. Вы знаете, какова его угловая скорость: сколько он поворачивает в единицу времени. Очевидно, что это один оборот в день!
Давайте спросим себя, какова линейная скорость шлюза на Панамском канале. Это достаточно близко к экватору, чтобы мы могли использовать диаметр земли на экваторе (12756 км) в качестве ориентира. Какова окружность Земли в этот момент?
Если вы рассчитаете длину окружности, вы можете умножить ее на угловую скорость, и вы получите линейную скорость.
Вот кое-что действительно интересное : Поскольку угловая скорость зависит от длины окружности (и, следовательно, от радиуса), вы можете иметь два объекта, движущихся с одинаковой угловой скоростью, но с разными линейными скоростями.
Давайте подумаем о (передней) звездочке, установленной на вашем велосипеде. Если вы перейдете с маленькой звездочки на большую и продолжите движение ног с тем же числом оборотов в минуту (с той же угловой скоростью), то вы будете двигаться быстрее. Это потому, что линейная скорость цепи определяет скорость велосипеда. Таким образом, когда вы переключали передачи, вы переходили от звездочки с малым радиусом (и, следовательно, с малой окружностью) к звездочке с большим радиусом (окружностью). Когда вы умножаете эти два числа на одну и ту же угловую скорость, вы получаете большую линейную скорость с большой звездочкой!
Таким образом, большая звездочка с вдвое большим радиусом, чем маленькая звездочка, должна позволить вам преодолеть вдвое большее расстояние за то же количество оборотов ног.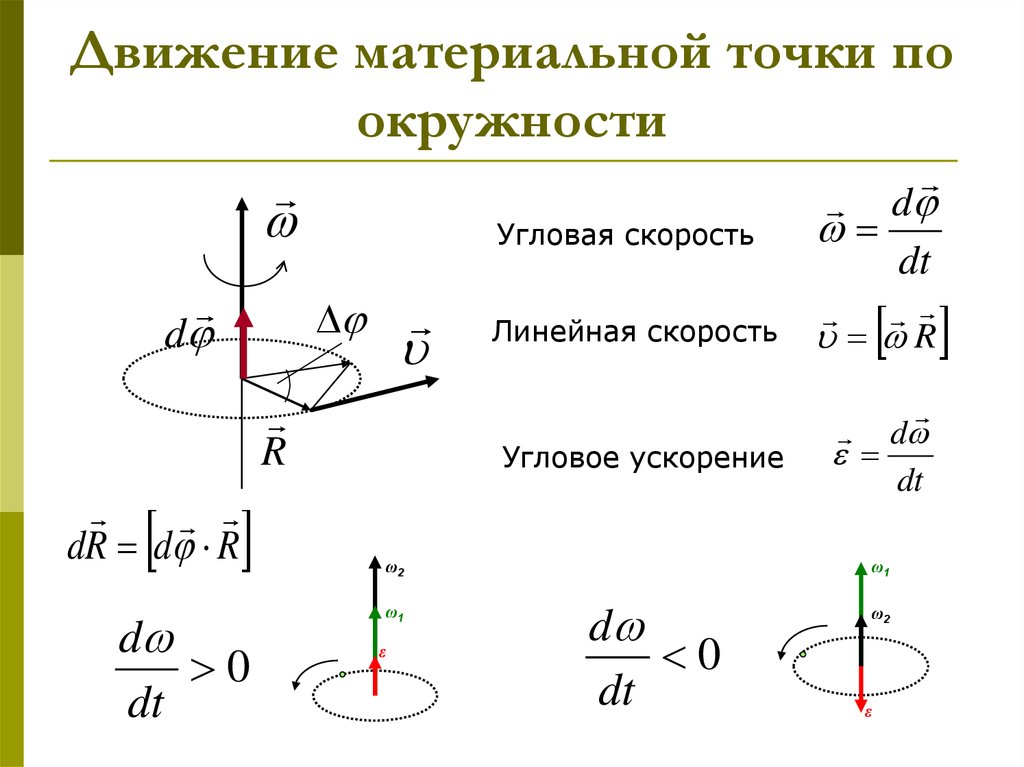
 Кроме того, предположим, что обоим \(A\) и \(B\) требуется 1 минута, чтобы пройти четверть окружности их соответствующих кругов (четверть полного оборота). Кто прошел наибольшее расстояние?
Кроме того, предположим, что обоим \(A\) и \(B\) требуется 1 минута, чтобы пройти четверть окружности их соответствующих кругов (четверть полного оборота). Кто прошел наибольшее расстояние?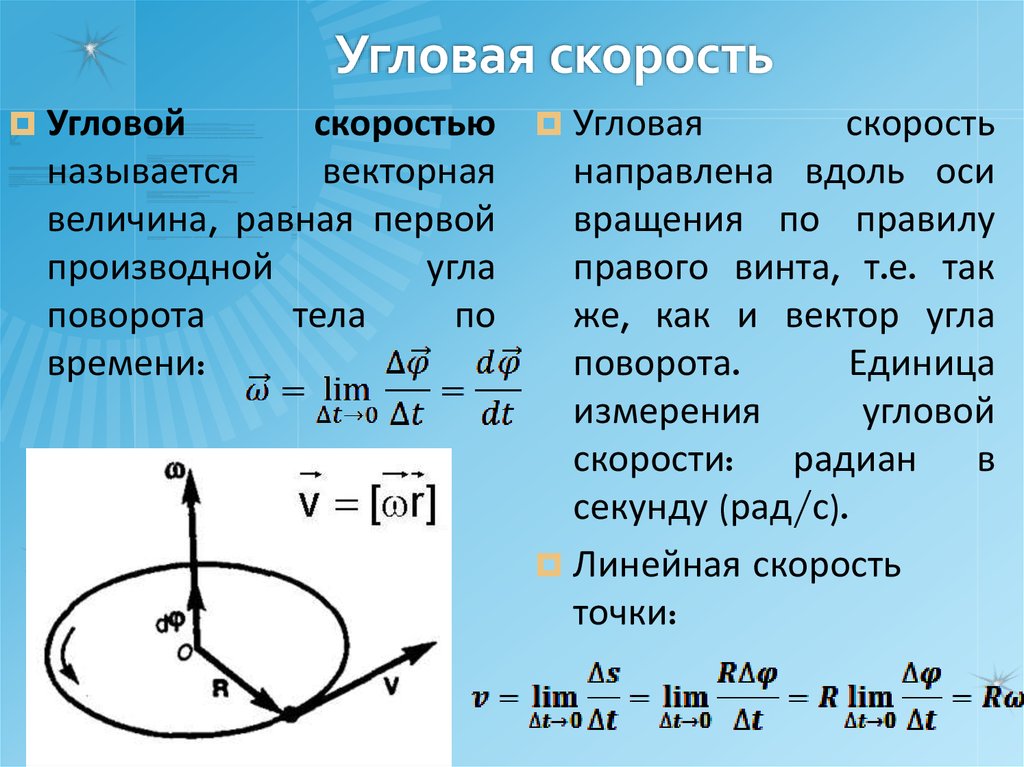

 линейная скорость — это длина дуги, пройденная точкой, деленная на прошедшее время. В то время как линейная скорость измеряет, как длина дуги изменяется во времени, угловая скорость является мерой того, насколько быстро изменяется центральный угол во времени. Угловая скорость точки представляет собой меру угла в радианах, деленную на время, которое требуется, чтобы выметать этот угол.
линейная скорость — это длина дуги, пройденная точкой, деленная на прошедшее время. В то время как линейная скорость измеряет, как длина дуги изменяется во времени, угловая скорость является мерой того, насколько быстро изменяется центральный угол во времени. Угловая скорость точки представляет собой меру угла в радианах, деленную на время, которое требуется, чтобы выметать этот угол. gvsu.edu/books/12
gvsu.edu/books/12