Содержание
Оборот в минуту. Конвертер величин. /
Конвертер угловой скорости, Обороты
Оборот в минуту. Конвертер величин. /
Конвертер угловой скорости, Обороты
EN
ES
PT
RU
FR
Ой… Javascript не найден.
Увы, в вашем браузере отключен или не поддерживается JavaScript.
К сожалению, без JavaScript этот сайт работать не сможет.
Проверьте настройки браузера, может быть JavaScript выключен случайно?
Оборот в минуту. Конвертер и таблица перевода величины.
| Всё очень просто: Нужна помощь? x Этот конвертер величин очень простой. Правда.
|
| ||||||||||
?Настройки конвертера:
x
Объяснение настроек конвертера
Кстати, пользоваться настройками не обязательно.
Вам вполне могут подойти настройки по умолчанию.
Количество значащих цифр
Для бытовых целей обычно не нужна высокая точность,
удобнее получить округлённый результат.
В таких случаях выберите 3 или 4 значащих цифры.
Максимальная точность — 9 значащих цифр.
Точность можно изменить в любой момент.
Разделитель групп разрядов
Выберите, в каком виде вам будет
удобно получить результат:
| 1234567.89 | нет |
|---|---|
| 1 234 567.89 | пробел |
| 1,234,567.89 | запятая |
1. 234.567,89 234.567,89 | точка |
- Значащих цифр:
1 23456789 - Разделитель разрядов:
нет пробел запятая точка
Укажите значение (Оборот в минуту):
» открыть »
» свернуть »
Обороты
| Оборот в минуту → Оборот в неделю | |
| Оборот в минуту → Оборот в сутки | |
| Оборот в минуту → Оборот в час | |
| Оборот в минуту → Оборот в секунду |
Единицы:
Оборот в неделю
/
Оборот в сутки
/
Оборот в час
/
/
Оборот в секунду
» открыть »
» свернуть »
Градусы
| Оборот в минуту → Градус в неделю | |
| Оборот в минуту → Градус в сутки | |
| Оборот в минуту → Градус в час | |
| Оборот в минуту → Градус в минуту | |
| Оборот в минуту → Градус в секунду |
Единицы:
Градус в неделю
/
Градус в сутки
/
Градус в час
/
Градус в минуту
/
Градус в секунду
» открыть »
» свернуть »
Радианы
Единица угловой скорости в системе СИ — радиан в секунду
| Оборот в минуту → Радиан в неделю | |
| Оборот в минуту → Радиан в сутки | |
| Оборот в минуту → Радиан в час | |
| Оборот в минуту → Радиан в минуту | |
| Оборот в минуту → Радиан в секунду |
Единицы:
Радиан в неделю
/
Радиан в сутки
/
Радиан в час
/
Радиан в минуту
/
Радиан в секунду
Не можете найти нужную единицу?
Попробуйте поискать:
Другие варианты:
Посмотрите алфавитный список всех единиц
Задайте вопрос на нашей странице в facebook
< Вернитесь к списку всех конвертеров
Надеемся, Вы смогли перевести все ваши величины,
и Вам у нас на Convert-me. Com понравилось. Приходите снова!
Com понравилось. Приходите снова!
!
Значение единицы приблизительное.
Либо точного значения нет,
либо оно неизвестно.
?
Пожалуйста, введите число.
(?)
Простите, неизвестное вещество. Пожалуйста, выберите что-то из списка.
***
Нужно выбрать вещество.
От этого зависит результат.
Совет: Не можете найти нужную единицу? Попробуйте поиск по сайту. Поле для поиска в верхней части страницы.
Нашли ошибку? Хотите предложить дополнительные величины? Свяжитесь с нами в Facebook.
Действительно ли наш сайт существует с 1996 года? Да, это так. Первая версия онлайнового конвертера была сделана ещё в 1995, но тогда ещё не было языка JavaScript, поэтому все вычисления делались на сервере — это было медленно. А в 1996г была запущена первая версия сайта с мгновенными вычислениями.
Для экономии места блоки единиц могут отображаться в свёрнутом виде. Кликните по заголовку любого блока, чтобы свернуть или развернуть его.
Слишком много единиц на странице? Сложно ориентироваться? Можно свернуть блок единиц — просто кликните по его заголовку. Второй клик развернёт блок обратно.
Наша цель — сделать перевод величин как можно более простой задачей. Есть идеи, как сделать наш сайт ещё удобнее? Поделитесь!
Минуточку, загружаем коэффициенты…
Равномерное движение по окружности. Скорость, ускорение
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: движение по окружности с постоянной по модулю скоростью, центростремительное ускорение.
Равномерное движение по окружности — это достаточно простой пример движения с вектором ускорения, зависящим от времени.
Пусть точка вращается по окружности радиуса . Скорость точки постоянна по модулю и равна . Скорость называется линейной скоростью точки.
Период обращения — это время одного полного оборота. Для периода имеем очевидную формулу:
Для периода имеем очевидную формулу:
. (1)
Частота обращения — это величина, обратная периоду:
.
Частота показывает, сколько полных оборотов точка совершает за секунду. Измеряется частота в об/с (обороты в секунду).
Пусть, например, . Это означает, что за время точка совершает один полный
оборот. Частота при этом получается равна: об/с; за секунду точка совершает 10 полных оборотов.
Угловая скорость.
Рассмотрим равномерное вращение точки в декартовой системе координат. Поместим начало координат в центре окружности (рис. 1).
| Рис. 1. Равномерное движение по окружности |
Пусть — начальное положение точки; иными словами, при точка имела координаты . Пусть за время точка повернулась на угол и заняла положение .
Отношение угла поворота ко времени называется угловой скоростью вращения точки:
. (2)
(2)
Угол , как правило, измеряется в радианах, поэтому угловая скорость измеряется в рад/с. За время, равное периоду вращения, точка поворачивается на угол . Поэтому
. (3)
Сопоставляя формулы (1) и (3), получаем связь линейной и угловой скоростей:
. (4)
Закон движения.
Найдём теперь зависимость координат вращающейся точки от времени. Видим из рис. 1, что
.
Но из формулы (2) имеем: . Следовательно,
. (5)
Формулы (5) являются решением основной задачи механики для равномерного движения точки по окружности.
Центростремительное ускорение.
Теперь нас интересует ускорение вращающейся точки. Его можно найти, дважды продифференцировав соотношения (5):
С учётом формул (5) имеем:
(6)
Полученные формулы (6) можно записать в виде одного векторного равенства:
(7)
где — радиус-вектор вращающейся точки.
Мы видим, что вектор ускорения направлен противоположно радиус-вектору, т. е. к центру окружности (см. рис. 1). Поэтому ускорение точки, равномерно движущейся по окружности, называется центростремительным.
е. к центру окружности (см. рис. 1). Поэтому ускорение точки, равномерно движущейся по окружности, называется центростремительным.
Кроме того, из формулы (7) мы получаем выражение для модуля центростремительного ускорения:
(8)
Выразим угловую скорость из (4)
и подставим в (8). Получим ещё одну формулу для центростремительного ускорения:
.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Равномерное движение по окружности.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
07.07.2023
Угловая скорость
Привет Бен.
Линейная скорость — это расстояние, пройденное по прямой за единицу времени. Угловая скорость – это угол, пройденный за единицу времени.
На сегодняшний день проще всего увидеть это в Равномерном круговом движении. Например, камешек, застрявший в шине вашего велосипеда, движется равномерно по окружности.
Допустим, внешний диаметр шины вашего велосипеда составляет 70 см, и вы движетесь со скоростью 40 км/ч. Помните, что (игнорируя занос) шина постоянно сохраняет сцепление с дорогой, поэтому расстояние, которое вы преодолеваете, и скорость, с которой вы едете, такие же, как и скорость шины. Если мы переведем эту скорость в метры в секунду, мы получим:
Это скорость велосипеда, то есть линейная скорость велосипеда. Поскольку велосипед и шина находятся в постоянном контакте, это также линейная скорость камешка в шине.
Угловая скорость связана с углами, как следует из названия. Выражается в виде того, на какой угол поворачивается за определенное время.
Выражается в виде того, на какой угол поворачивается за определенное время.
Углы можно измерять разными способами: поворотами, градусами и радианами. Например, жесткий диск со скоростью 10 000 об/мин относится к его угловой скорости: 10 000 оборотов в минуту. Итак, с какой скоростью вращается наш камешек?
Этот камешек, как мы знаем, движется линейно со скоростью, эквивалентной 11,11 м/с, но он движется по окружности шины. Если внешний диаметр шины d равен 70 см, то длина окружности равна πd , что составляет около 2,199 м.
Если мы разделим линейную скорость на длину окружности шины, мы узнаем, сколько оборотов в секунду совершает эта шина (и, следовательно, камешек) — под углом:
, где R = обороты.
Это угловая скорость: на сколько поворачивает в единицу времени. Если вы хотите преобразовать это в градусы, вы просто умножаете на количество градусов на оборот (360), если вы хотите вместо этого использовать радианы, умножьте на 2π радиан на оборот.
Теперь попробуем в другом направлении. Допустим, вы знаете угловую скорость и пытаетесь вычислить соответствующую линейную скорость. Подсказка: это довольно быстро!
Возьмем в качестве примера вращение Земли. Вы знаете, какова его угловая скорость: сколько он поворачивает в единицу времени. Очевидно, что это один оборот в день!
Давайте спросим себя, какова линейная скорость шлюза на Панамском канале. Это достаточно близко к экватору, чтобы мы могли использовать диаметр земли на экваторе (12756 км) в качестве ориентира. Какова окружность Земли в этот момент?
Если вы рассчитаете длину окружности, вы можете умножить ее на угловую скорость, и вы получите линейную скорость.
Вот кое-что действительно интересное : Поскольку угловая скорость зависит от длины окружности (и, следовательно, от радиуса), вы можете иметь два объекта, движущихся с одинаковой угловой скоростью, но с разными линейными скоростями.
Давайте подумаем о (передней) звездочке, установленной на вашем велосипеде. Если вы перейдете с маленькой звездочки на большую и продолжите движение ног с тем же числом оборотов в минуту (с той же угловой скоростью), то вы будете двигаться быстрее. Это потому, что линейная скорость цепи определяет скорость велосипеда. Таким образом, когда вы переключали передачи, вы переходили от звездочки с малым радиусом (и, следовательно, с малой окружностью) к звездочке с большим радиусом (окружностью). Когда вы умножаете эти два числа на одну и ту же угловую скорость, вы получаете большую линейную скорость с большой звездочкой!
Таким образом, большая звездочка с вдвое большим радиусом, чем маленькая звездочка, должна позволить вам преодолеть вдвое большее расстояние за то же количество оборотов ног.
Подводя итог:
- Разделите линейную скорость на длину окружности, чтобы получить угловую скорость (в оборотах в единицу времени, которую вы затем можете преобразовать в любую другую интересующую вас единицу).

- Умножьте угловую скорость (в оборотах в единицу времени — сначала преобразуйте, если нужно) на длину окружности, чтобы получить линейную скорость.
Надеюсь, вам все стало ясно!
Стивен Ла Рок>
Калькулятор угловой скорости
Автор Wojciech Sas, PhD
Отзыв от Bogna Szyk и Jack Bowater
Последнее обновление: 05 июня 2023 г.
Содержание:
- Что такое угловая скорость?
- Формулы для угловой скорости
- Единицы измерения угловой скорости
- Зависимость угловой скорости от угловой частоты
- Как найти угловую скорость Земли?
- Физические величины, зависящие от угловой скорости
- Сохранение углового момента
- Часто задаваемые вопросы
Этот калькулятор угловой скорости представляет собой простой в использовании инструмент, который дает немедленный ответ на вопрос: » Как найти угловую скорость? «.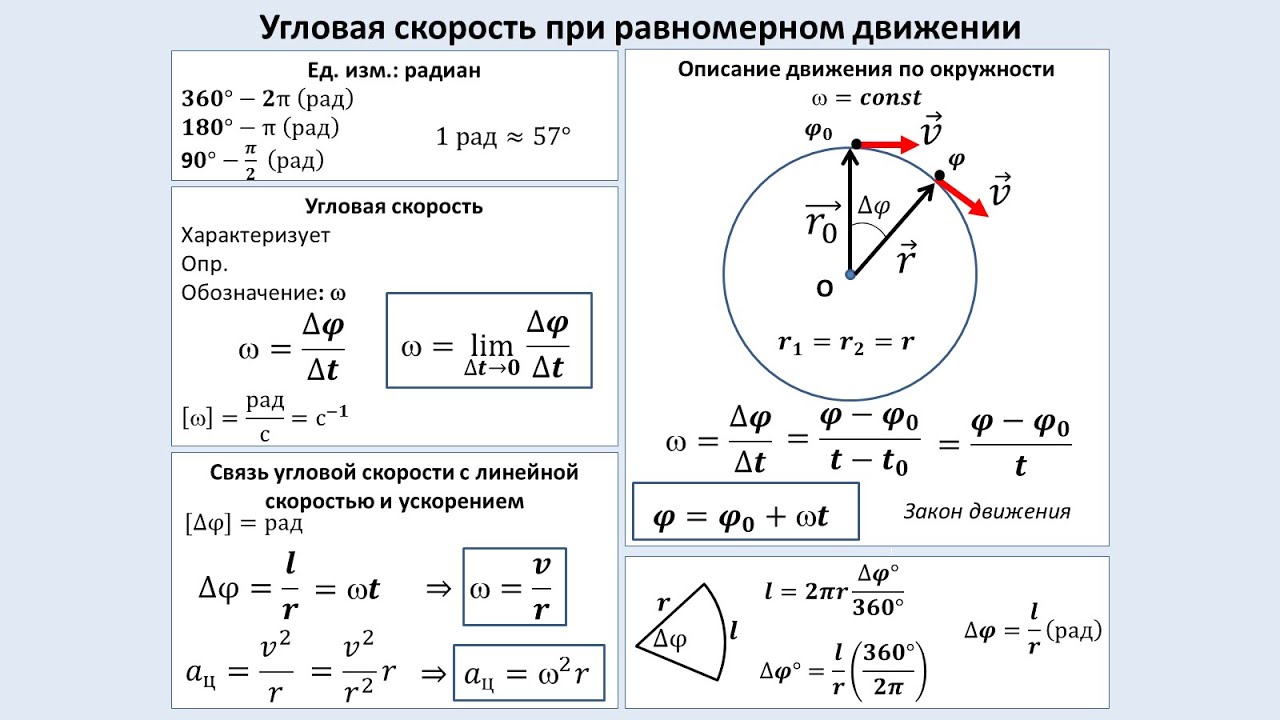 В тексте вы найдете несколько формул угловой скорости , узнаете о различных единицах угловой скорости и, наконец, оцените угловую скорость Земли!
В тексте вы найдете несколько формул угловой скорости , узнаете о различных единицах угловой скорости и, наконец, оцените угловую скорость Земли!
Задумывались ли вы когда-нибудь, какова связь между угловой скоростью и угловой частотой ? Или где применяется угловая скорость? Читайте дальше, чтобы узнать, и стать экспертом в области кругового движения.
🙋 Перейдите к нашему калькулятору кругового движения, чтобы также узнать о других важных величинах для вращающегося тела.
Что такое угловая скорость?
Угловая скорость описывает вращательное движение тел. Он измеряет, насколько быстро они движутся вокруг некоторого центра вращения. Мы можем думать о двух разных видах вращения. Первый описывает движение центра масс данного объекта вокруг определенной точки в пространстве , которую мы можем описать как начало координат. Некоторые примеры включают планеты, движущиеся вокруг Солнца, или автомобиль, съезжающий с шоссе.
Второй примерно вращение тела вокруг собственного центра масс – спин (не путать с квантовым свойством частиц, также называемым спином). Наверняка вы видели, как баскетболист крутит мяч на пальце.
В целом можно сказать, что чем быстрее движение, тем выше угловая скорость. Мы должны перейти к уравнениям угловой скорости, описанным в следующем разделе, чтобы определить некоторые конкретные значения.
Формулы угловой скорости
Этот калькулятор угловой скорости использует две разные формулы угловой скорости в зависимости от ваших входных параметров.
Первое уравнение угловой скорости аналогично уравнению линейной скорости:
ω=α2−α1t=Δαt,\omega = \frac{\alpha_2 — \alpha_1}{t} = \frac{\Delta\alpha} {t},ω=tα2−α1=tΔα,
где α1\alpha_1α1 и α2\alpha_2α2 — два значения углов на окружности, а Δα\Delta\alphaΔα — их разность. ttt – время, за которое происходит изменение угла. Как видите, для нормальной скорости есть отношение смещения положения за период, а здесь мы используем угол вместо расстояния.
Формулу второй угловой скорости можно вывести из соотношения линейной скорости и радиуса, используя векторное произведение, которое равно:
v⃗=ω⃗×r⃗\vec{v} = \vec{\omega} \times \ vec{r}v 92},ω
=∣r∣2r
×v
,
, где все эти переменные являются векторами , а ∣r∣|r|∣r∣ обозначает абсолютное значение радиуса. Фактически угловая скорость представляет собой псевдовектор, направление которого перпендикулярно плоскости вращательного движения.
Единицы измерения угловой скорости
Существует несколько единиц измерения угловой скорости, и те, которые мы используем в нашем калькуляторе угловой скорости, перечислены ниже:
рад/сили радиан в секунду – определение исходит прямо из первой формулы угловой скорости. Он говорит, насколько велик поворот (или угол), на который тело движется за заданное время.RPMили оборотов в минуту – Наиболее часто встречающаяся в практическом применении единица. С его помощью можно описать, как быстро вращается колесо или двигатель. Вы можете легко себе представить разницу между
С его помощью можно описать, как быстро вращается колесо или двигатель. Вы можете легко себе представить разницу между 10и100 об/мин.Гцили герц – Те же единицы, которые используются для частоты, но редко используются в контексте угловой скорости. Это чем-то похоже наоб/мин, говорящее нам, сколько полных оборотов сделано за заданное время. Разница в том, что раньше основной единицей времени была минута, а здесь – секунда.
Естественно, все эти единицы угловой скорости преобразуются между собой с помощью следующих соотношений:
1 RMP = 0,10472 рад/с = 0,01667 Гц ,
или наоборот:
1 Гц = 6,283 рад/с = 60 об/мин .
Угловая скорость в зависимости от угловой частоты
Посмотрите определение угловой частоты:
ω=2πf,\omega = 2\pi f,ω=2πf,
где fff – частота. Как мы видим, он обозначается той же буквой. Кроме того, единицей угловой частоты является 90 154 рад/с 90 155, точно такая же, как и для угловой скорости. Поэтому может возникнуть вопрос: «Чем отличается угловая скорость от угловой частоты?».
Кроме того, единицей угловой частоты является 90 154 рад/с 90 155, точно такая же, как и для угловой скорости. Поэтому может возникнуть вопрос: «Чем отличается угловая скорость от угловой частоты?».
Ответ относительно прост. Связь между угловой частотой и угловой скоростью аналогична связи между скоростью и скоростью . Первое есть величина второго; другими словами, угловая частота является скаляром, тогда как угловая скорость является (псевдо)вектором.
Обычно мы используем угловую частоту, когда говорим о гармоническом движении , примером которого является простой маятник. Как вы понимаете, движение не обязательно должно быть представлено стандартным вращением, а просто движением, которое периодически повторяет свое положение. Однако угловая скорость строго связана с движением вокруг некоторой точки. Поэтому можно сказать, что угловая частота — это более общая величина , и мы можем использовать ее для описания широкого круга физических задач. Напротив, угловая скорость включает только вращательное движение.
Напротив, угловая скорость включает только вращательное движение.
🙋 У нас есть специальный инструмент, который объясняет, как рассчитать угловую частоту. Обязательно проверьте калькулятор угловой частоты!
Как найти угловую скорость Земли?
Как насчет использования нашего калькулятора угловой скорости? Оценим угловую скорость Земли! Во-первых, мы учитываем скорость вращения. Мы знаем, что Земля совершает полный оборот относительно далеких звезд примерно за 23 ч 56 мин 4 с , что составляет примерно 23,934 ч . Весь поворот составляет угол 2π рад , поэтому результирующая угловая скорость:
\omega_1 &= 2\pi\ \rm рад / 23,934\ ч\\
&= 0,2625\ \rm рад/ч\\
&= 0,00007292\ \rm рад/с,
\end{split}ω1=2π рад/23,934 ч=0,2625 рад/ч=0,00007292 рад/с,
9{-5}\ \rm рад/с7,292×10-5 рад/с (в экспоненциальном представлении).
Теперь, когда мы знаем угловую скорость вращения Земли, мы можем оценить ее линейную скорость на экваторе. {-7}\ \rm рад/с,
{-7}\ \rm рад/с,
\end{split}ω2=2π рад/23,9{-7}\, рад/с\\
&= 29,785\ \rm км/с
\end{split}v2=1,496×108км⋅1,991×10−7рад/с=29,785 км/с
Мы движемся довольно быстро, не так ли?
Физические величины, зависящие от угловой скорости
Несколько физических величин связаны с угловой скоростью, некоторые из которых перечислены ниже:
Угловое ускорение – Описывает изменение угловой скорости во времени. Чем выше разница угловых скоростей, тем больше значение углового ускорения. Не стесняйтесь проверить, как это работает на практике, с помощью нашего калькулятора углового ускорения.
Кинетическая энергия вращения – Мера энергии при круговом движении. Как и в случае с кинетической энергией, зависимость (угловой) скорости является квадратичной.
Центробежная сила – Ее можно почувствовать в автомобиле при повороте. Чем быстрее вы выполняете поворот или чем он круче, тем выше становится центробежная сила, которую мы отчетливо чувствуем.

Эффект Кориолиса — Это заставляет объекты поворачиваться, если они находятся на вращающемся теле (например, на Земле), вместо того, чтобы двигаться по прямой линии.
Система шкивов – Это не физическая величина, точнее говоря, это интересное устройство, которое полностью связано с угловой скоростью. Простейшая система состоит из двух шкивов, обычно с разными окружностями или радиусами. Их соединяет пояс, поэтому их линейные скорости одинаковы , но так как они разного размера, их угловые скорости изменяются пропорционально . Зная это и имея какой-нибудь двигатель с вполне определенной скоростью вращения, мы можем с хорошей точностью задавать угловую скорость выходного элемента, просто регулируя его размер.
Сохранение углового момента
Несколько фундаментальных правил говорят нам о величинах, сохраняющихся в изолированных системах. Наиболее известны законы сохранения энергии и сохранения импульса. Вместе с ними существует также закон сохранения момента импульса . Если мы подумаем о двух моментах времени, мы можем записать правило как:
Вместе с ними существует также закон сохранения момента импульса . Если мы подумаем о двух моментах времени, мы можем записать правило как:
где I1I_1I1 и I2I_2I2 — начальный и конечный моменты инерции масс соответственно; эти величины, которые описывают распределение массы относительно центра тел.
Мы видим, что при увеличении момента инерции угловая скорость уменьшается, и наоборот . Итак, каковы последствия этого явления?
Представим, что вы фигурист. Когда вы вращаетесь, вы обладаете некоторой угловой скоростью. Если ваши руки широко раскрыты, момент инерции масс относительно велик . Затем вы приближаете руки к остальной части тела. Как следствие, ваш момент инерции уменьшается на , поэтому, поскольку общий угловой момент должен сохраняться, ваш угловая скорость увеличивается — значит, вы будете крутиться быстрее! Это не магия, просто физика!
Если вы не умеете/не любите кататься на коньках, можете попробовать проверить правило на обычном вращающемся стуле.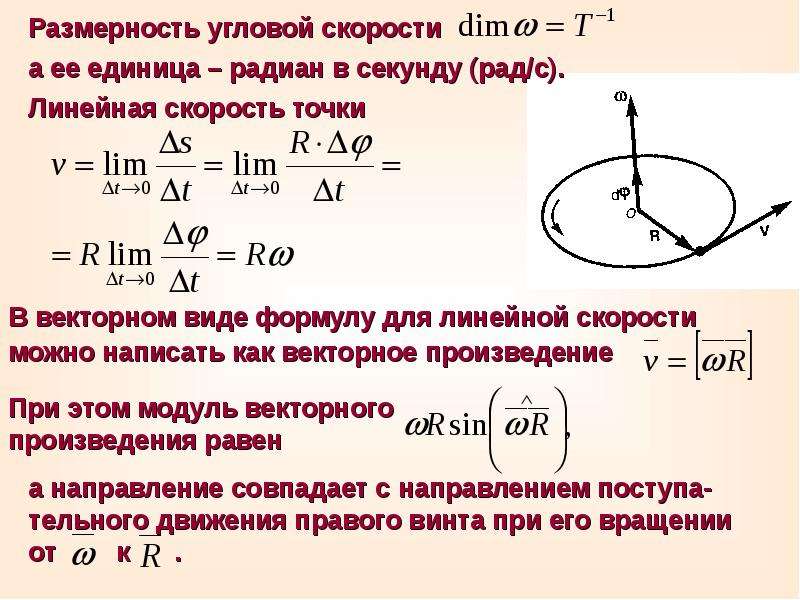 Просто помните, безопасность превыше всего! Убедитесь, что есть достаточно места для проведения этого эксперимента. После этого просто начните вращаться и посмотрите, как изменится ваша угловая скорость, когда вы двигаете руками вперед и назад. Кроме того, вы можете усилить эффект, используя гантели. В результате вы можете совместить и упражнения, и развлечение в одно целое!
Просто помните, безопасность превыше всего! Убедитесь, что есть достаточно места для проведения этого эксперимента. После этого просто начните вращаться и посмотрите, как изменится ваша угловая скорость, когда вы двигаете руками вперед и назад. Кроме того, вы можете усилить эффект, используя гантели. В результате вы можете совместить и упражнения, и развлечение в одно целое!
Часто задаваемые вопросы
Равна ли угловая скорость v×r?
№ . Чтобы рассчитать величину угловой скорости ω от линейной скорости V и радиуса R , мы разделяем эти величины:
ω = V / R
В этом случае, угловая скорость — рад/с (радиан в секунду).
Какова формула угловой скорости для постоянного углового ускорения?
формула угловой скорости в данном случае:
ω = ω 0 + αt
где:
- ω – угловая скорость;
- ω 0 – начальная угловая скорость;
- α – Угловое ускорение; и
- t – Продолжительность события.



 С его помощью можно описать, как быстро вращается колесо или двигатель. Вы можете легко себе представить разницу между
С его помощью можно описать, как быстро вращается колесо или двигатель. Вы можете легко себе представить разницу между 
