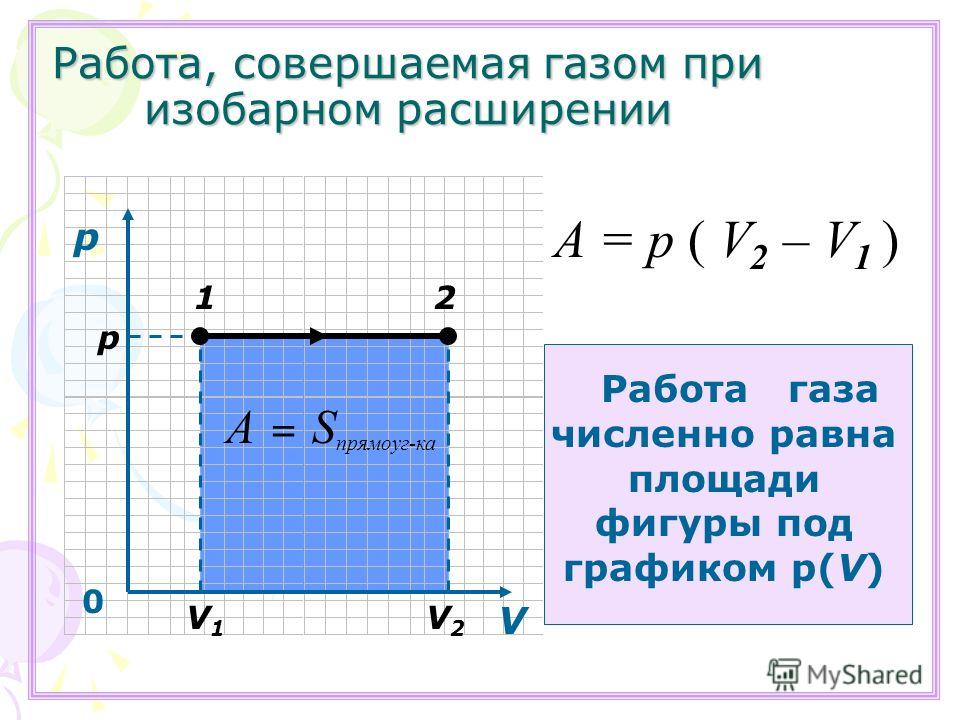
| ||||||||
| Специальный поиск | ||||||||
|
Физика
Теория вероятностей и мат. статистика
Гидравлика
Теор. механика
Прикладн. механика
Химия
Электроника
Витамины для ума
| Главная Поиск по сайту Формулы Все задачи Помощь Контакты Билеты
| |||||||
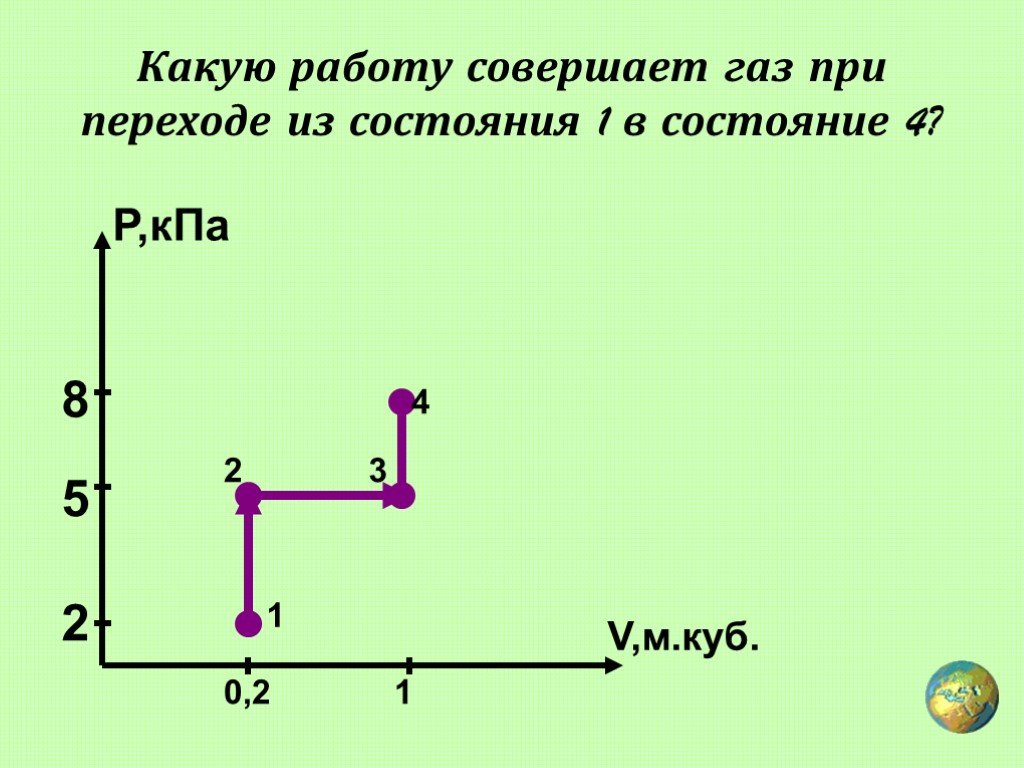
какую работу совершит газ Задача 50144 При медленном изотермическом процессе газу передано 8·106 Дж теплоты. Какую работу совершил газ? Что произойдет с его объемом?
Задача 50399 При изотермическом расширении одного моля водорода была затрачена теплота 4 кДж, при этом объем водорода увеличился в пять раз.
Задача 14706 Определить количество теплоты, сообщенное 88 г углекислого газа, если он был нагрет от 300 К до 350 К при постоянном давлении. Какую работу при этом может совершить газ и как изменится его внутренняя энергия?
Задача 15549 Над газом провели некоторый процесс, в ходе которого он отдал 5,2 кДж теплоты. Какую работу совершили над газом, если он перешёл из состояния с внутренней энергией 6,2 кДж в состояние с внутренней энергией 4,3 кДж? Ответ выразить в кДж, округлив до десятых.
Задача 15700 Над газом провели некоторый процесс, в ходе которого он отдал 5,2 кДж теплоты. Какую работу совершили над газом, если он перешёл из состояния с внутренней энергией 6,2 кДж в состояние с внутренней энергией 4,3 кДж? Ответ выразить в кДж, округлив до десятых.
Задача 16181 Азот массой m = 100 г нагревают при постоянном давлении от температуры t1 = 20 °С до t2 = 220 °С. Какое количество теплоты Q поглощается при этом? Каков прирост внутренней энергии ΔU газа? Какая работа А совершается газом?
Задача 22630 Идеальный газ, расширяясь изотермически при Т = 300 К, переходит из состояния, соответствующего адиабате со значением энтропии S1 = 13,6 Дж/К, в другое состояние, соответствующее адиабате со значением S2 = 210,6 Дж/К. Какую работу совершает газ в ходе этого процесса?
Задача 24034 Определить количество теплоты, сообщенное 100 г углекислого газа, если он был изобарически нагрет от 250 К до 350 К. Какую работу при этом может совершить газ и как изменится его внутренняя энергия?
| ||||||||
Задачи на первый закон термодинамики
Первый закон термодинамики .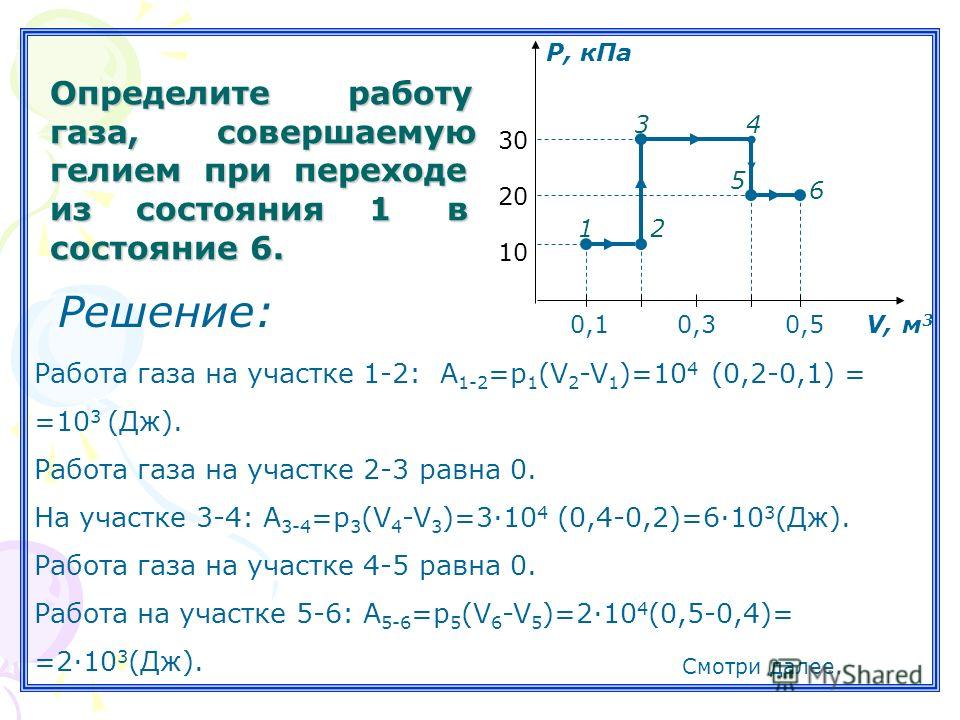
\( Q=\Delta U+A \)
\(Q\) — Количество теплоты, полученное газом
Если \(\; Q>0 \; ,\) то газ получает тепло
Если \(\; Q < 0 \; , \) то газ отдает тепло
\( \Delta U \)-Изменение внутренней энергии газа
\(A\) — Работа газа
\(A=P \Delta V \)
\( \Delta V \)- Изменение объема газа
Если изменение объема газа равно нулю \(( \Delta V =0) \), то и работа газа равна нулю
Если газ расширяется , то \(\; A>0 \; ,\) (газ совершает положительную работу)
Если газ сужается , то \(\; A < 0 \; , \) и говорят:»Внешние силы совершают работу над газом «
или » Работа газа отрицательна »
Задача 1.
Внутренняя энергия идеального газа возрастает на 300 Джоулей \((\Delta U=300 Дж) \; , \)
при этом газ совершает работу \(A=200 Дж \; . \)
Какое количество теплоты получил газ?
Показать ответ
Показать решение
Видеорешение
Ответ: \( Q=500 Дж \)
Запишем уравнение Первого закона термодинамики:
Дано:
\(\Delta U=300 Дж\)
\(A=200 Дж \)
\(Q-? \)
\( Q=\Delta U+A \)
\( Q=300 Дж+200 Дж=500 Дж \)
Ответ: \( Q=500 Дж \)
Задача 2.
Газ получает из внешней среды \(Q=500 Дж \; , \) при этом газ совершает работу \(A=200 Дж \; . \)
Найти изменение внутренней энергии \( \Delta U \; .\)
Показать ответ
Показать решение
Видеорешение
Ответ: \( \Delta U= 300 Дж \)
Запишем уравнение Первого закона термодинамики:
Дано:
\(Q=500 Дж \)
\(A=200 Дж \)
\(\Delta U-? \)
\( Q=\Delta U+A \)
\( \Delta U=Q-A \)
\( \Delta U= 500 Дж- 200 Дж=300 Дж \)
Ответ: \( \Delta U= 300 Дж \)
Задача 3.
Газ получает из внешней среды \(Q=700 Дж \; , \) при этом внутренняя энергия газа возрастает
на 150 Джоулей \( (\Delta U=150 Дж) \; .\)
Какую работу совершает газ?
Показать ответ
Показать решение
Видеорешение
Ответ: \( A= 550 Дж \)
Запишем уравнение Первого закона термодинамики:
Дано:
\(Q=700 Дж \)
\( \Delta U=150 Дж \)
\(A-? \)
\( Q=\Delta U+A \)
\( A=Q-\Delta U \)
\( A= 700 Дж-150 Дж=550 Дж \)
Ответ: \( A= 550 Дж \)
Задача 4.
Газ получает из внешней среды \(Q=1700 Дж \; , \) при этом внутренняя энергия газа возрастает
на 250 Джоулей \( (\Delta U=250 Дж) \; .\)
Какую работу совершает газ?
Показать ответ
Показать решение
Видеорешение
Ответ: \( A= 1450 Дж \)
Запишем уравнение Первого закона термодинамики:
Дано:
\(Q=1700 Дж \)
\( \Delta U=250 Дж \)
\(A-? \)
\( Q=\Delta U+A \)
\( A=Q-\Delta U \)
\( A= 1700 Дж-250 Дж=1450 Дж \)
Ответ: \( A= 1450 Дж \)
Задача 5.
Внутренняя энергия идеального газа уменьшается на 300 Джоулей \((\Delta U=-300 Дж) \; , \)
при этом газ совершает работу \(A=500 Дж \; . \)
Какое количество теплоты получил газ?
Показать ответ
Показать решение
Видеорешение
Ответ: \( Q=200Дж \)
Запишем уравнение Первого закона термодинамики:
Дано:
\(A=500 Дж \)
\( \Delta U=-300 Дж \)
\(Q-? \)
\( Q=\Delta U+A \)
\( Q=-300 Дж+500 Дж=200Дж \)
Ответ: \( Q=200Дж \)
Задача 6.
Внутренняя энергия идеального газа уменьшается на 400 Джоулей \((\Delta U=-400 Дж) \; , \)
при этом газ совершает работу \(A=450 Дж \; . \)
Какое количество теплоты получил газ?
Показать ответ
Показать решение
Видеорешение
Ответ: \( Q=50Дж \)
Запишем уравнение Первого закона термодинамики:
Дано:
\(A=450 Дж \)
\( \Delta U=-400 Дж \)
\(Q-? \)
\( Q=\Delta U+A \)
\( Q=-400 Дж+450 Дж=50Дж \)
Ответ: \( Q=50Дж \)
Задача 7.
Внутренняя энергия идеального газа уменьшается на 500 Джоулей \((\Delta U=-500 Дж) \; , \)
при этом газ совершает работу \(A=500 Дж \; . \)
Какое количество теплоты получил газ?
Показать ответ
Показать решение
Видеорешение
Ответ: \( Q=0Дж \;\;\;\;\;\;\;\; \) Газ не получил тепло
Запишем уравнение Первого закона термодинамики:
Дано:
\(A=500 Дж \)
\( \Delta U=-500 Дж \)
\(Q-? \)
\( Q=\Delta U+A \)
\( Q=-500 Дж+500 Дж=0 Дж \)
Ответ: \( Q=0Дж \)
Газ не получил тепло , это адиабатный процесс, процесс идущий без теплообмена с окружающей средой
Задача 8.
Внутренняя энергия идеального газа уменьшается на 500 Джоулей \((\Delta U=-500 Дж) \; , \)
при этом газ совершает работу \(A=200 Дж \; . \)
Какое количество теплоты получил(или отдал) газ?
Показать ответ
Показать решение
Видеорешение
Ответ: \( Q=-300Дж \;\;\;\;\;\;\;\; \) Газ не получил тепло,а отдал во внешнюю среду
Запишем уравнение Первого закона термодинамики:
Дано:
\(A=200 Дж \)
\( \Delta U=-500 Дж \)
\(Q-? \)
\( Q=\Delta U+A \)
\( Q=-500 Дж+200 Дж=-300 Дж \)
Ответ: \( Q=-300Дж \)
Газ не получил тепло , а отдал во внешнюю среду 300 Джоулей
Задача 9.
Внутренняя энергия идеального газа уменьшается на 1200 Джоулей \((\Delta U=-1200 Дж) \; , \)
при этом газ совершает работу \(A=400 Дж \; . \)
\)
Какое количество теплоты получил(или отдал) газ?
Показать ответ
Показать решение
Видеорешение
Ответ: \( Q=-800Дж \;\;\;\;\;\;\;\; \)
Газ не получил тепло,а отдал во внешнюю среду
Запишем уравнение Первого закона термодинамики:
Дано:
\(A=400 Дж \)
\( \Delta U=-1200 Дж \)
\(Q-? \)
\( Q=\Delta U+A \)
\( Q=-1200 Дж+400 Дж=-800 Дж \)
Ответ: \( Q=-800Дж \)
Газ не получил тепло , а отдал во внешнюю среду 800 Джоулей
Задача 10.
Газ отдал во внешнюю среду 40 Джоулей \( (Q=-40 Дж ) \; , \) при этом
внутренняя энергия газа уменьшается на 120 Джоулей \((\Delta U=-120 Дж) . \)
Найти совершенную газом работу.
Показать ответ
Показать решение
Видеорешение
Ответ: \( A=80 Дж \)
Запишем уравнение Первого закона термодинамики:
Дано:
\(Q=-40 Дж \)
\( \Delta U=-120 Дж \)
\(A-? \)
\( Q=\Delta U+A \)
\(-40 Дж =-120 Дж+A \)
\(-40 Дж +120 Дж=A \)
\(A=80 Дж \)
Ответ: \( A=80 Дж \)
Задача 11.
Газ отдал во внешнюю среду 85 Джоулей \( (Q=-85 Дж ) \; , \) при этом
внутренняя энергия газа уменьшается на 135 Джоулей \((\Delta U=-135 Дж) . \)
Найти совершенную газом работу.
Показать ответ
Показать решение
Видеорешение
Ответ: \( A=50 Дж \)
Запишем уравнение Первого закона термодинамики:
Дано:
\(Q=-85 Дж \)
\( \Delta U=-135 Дж \)
\(A-? \)
\( Q=\Delta U+A \)
\(-85 Дж =-135 Дж+A \)
\(-85 Дж +135 Дж=A \)
\(A=50 Дж \)
Ответ: \( A=50 Дж \)
Задача 12.
Газ отдал во внешнюю среду 180 Джоулей \( (Q=-180 Дж ) \; , \) при этом
внутренняя энергия газа уменьшается на 100 Джоулей \((\Delta U=-100 Дж) . \)
Найти совершенную газом работу.
Показать ответ
Показать решение
Видеорешение
Ответ: \( A=-80 Дж \)
Запишем уравнение Первого закона термодинамики:
Дано:
\(Q=-180 Дж \)
\( \Delta U=-100 Дж \)
\(A-? \)
\( Q=\Delta U+A \)
\(-180 Дж =-100 Дж+A \)
\(-180 Дж +100 Дж=A \)
\(A=-80 Дж \)
Работа газа отрицательна, значит газ сжался (объем газа уменьшился),
Внешние силы совершили работу над газом \(A_{внешних сил}= 80 Дж \)
Ответ: \( A=-80 Дж \)
Задача 13.
Работа внешних сил над газом равна 200 Дж \( (A=-200 Дж) \)
при этом
внутренняя энергия газа увеличивается на 300 Джоулей \((\Delta U=300 Дж) . \)
Какое количество теплоты получил газ?
Показать ответ
Показать решение
Видеорешение
Ответ: \( Q= 100 Дж \)
Запишем уравнение Первого закона термодинамики:
Дано:
\( A=-200 Дж \)
\( \Delta U=300 Дж \)
\(Q -? \)
\( Q=\Delta U+A \)
\(Q= -200 Дж + 300 Дж \)
\( Q= 100 Дж \)
Газ получил 100 Джоулей
Ответ: \( Q= 100 Дж \)
Задача 14.
Внешние силы совершают над газом работу 800 Дж \( (A=-800 Дж) \)
при этом
внутренняя энергия газа увеличивается на 800 Джоулей \((\Delta U=800 Дж) . \)
Какое количество теплоты получил газ?
Показать ответ
Показать решение
Видеорешение
Ответ: \( Q= 0 Дж \)
Запишем уравнение Первого закона термодинамики:
Дано:
\( A=-800 Дж \)
\( \Delta U=800 Дж \)
\(Q -? \)
\( Q=\Delta U+A \)
\(Q= -800 Дж + 800 Дж \)
\( Q= 0 Дж \)
Ответ: \( Q= 0 Дж \)
Газ не получил тепло , это адиабатный процесс, процесс идущий без теплообмена с окружающей средой
Задача 15.
Газ получает количество теплоты 500 Джоулей, при этом его внутрення энергия возрастает на 500 Джоулей.
Какую работу совершает газ?
Показать ответ
Показать решение
Видеорешение
Ответ: \( A= 0 Дж \)
Запишем уравнение Первого закона термодинамики:
Дано:
\( Q=500 Дж \)
\( \Delta U=500 Дж \)
\(A -? \)
\( Q=\Delta U+A \)
\(500 Дж= 500 Дж + A \)
\( A= 0 Дж \)
Газ не совершает работу
Ответ: \( A= 0 Дж \)
Термодинамика — раздел физики Состояние газа определяется Ученые определяют работу W как продукт Вт = F * с Для газа работа есть произведение Вт = р * В Мы можем сделать W = (сила / площадь) * (площадь * длина) = сила * длина В метрической системе единицей работы является джоуль, в английской системе W = S [p] dV На графике Как упоминалось выше, существует несколько вариантов изменения состояния Обратите внимание, что не только работа, совершаемая газом, зависит от процесса, но и Деятельность: Экскурсии с гидом
Навигация ..
|
Работа
Работа
Работа
| Определение работы | Тепло и работа | Сохранение энергии | Внутренняя энергия |
| Взаимное превращение тепла и работы | Функции состояния | Калориметр | |
Определение работы
Работа может быть определена как произведение силы, используемой для перемещения
объект, умноженный на расстояние, на которое перемещается объект.
ш = F x г
Представьте себе систему, состоящую из образца аммиака, запертого в поршне и цилиндре,
как показано на рисунке ниже. Предположим, что давление газа, давит на поршень
просто уравновешивает вес поршня, так что объем газа остается постоянным. Сейчас
считать, что газ разлагается с образованием азота и водорода, увеличивая количество газа
частицы в контейнере. Если температура и давление газа остаются постоянными,
это означает, что объем газа должен увеличиться.
2 NH 3 ( г )
N 2 ( г ) + 3 H 2 ( г )
Объем газа можно увеличить, частично вытолкнув поршень из цилиндра.
Совершаемая работа равна произведению силы, действующей на поршень, на
расстояние, на которое перемещается поршень.
ш = F x г
Давление ( P ), которое газ оказывает на поршень, равно силе (F)
с которой он давит на поршень, деленную на площадь поверхности ( A )
поршень.
Таким образом, сила, действующая на газ, равна произведению его давления на
площадь поверхности поршня.
F = P x А
Подстановка этого выражения в уравнение, определяющее работу, дает следующее
результат.
w = ( P x A ) x d
Произведение площади поршня на расстояние, на которое перемещается поршень, равно
изменение объема системы при расширении газа. Условно,
изменение объема представлено символом В .
В
= А x d
Таким образом, величина работы, совершаемой при расширении газа, равна произведению
давление газа, умноженное на изменение объема газа.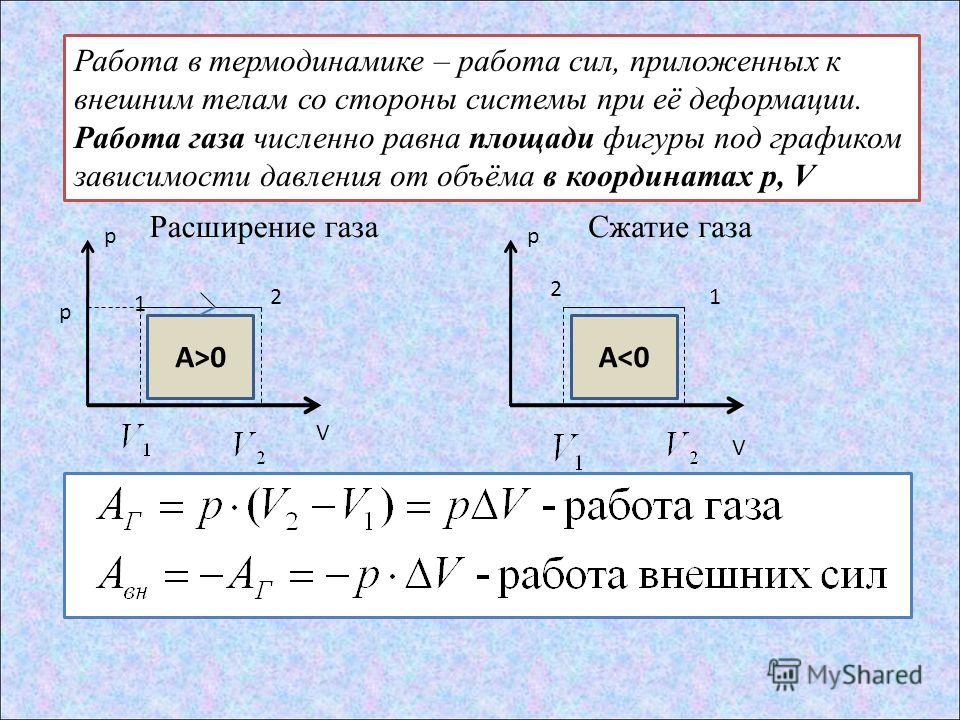
| с | = П В
Джоуль – измерение теплоты и работы
По определению, один джоуль — это работа, совершаемая, когда сила в один ньютон используется для перемещения
объект один метр.
1 Дж = 1 Н·м
Поскольку работа может быть преобразована в теплоту и наоборот, в системе СИ джоуль используется для
измерять энергию в виде теплоты и работы.
Первый закон термодинамики: сохранение
Энергия
Первый закон термодинамики гласит, что энергия не может быть создана или
уничтожен. Система может получать или терять энергию. Но любое изменение энергии системы
должно сопровождаться эквивалентным изменением энергии его окружения, потому что
полная энергия Вселенной постоянна. Первый закон термодинамики можно описать
следующим уравнением.
E унив
= E сис
+ E доп.
= 0
(Индексы univ , sys и surr обозначают вселенную,
системы и ее окружения.)
Внутренняя энергия
Энергию системы часто называют ее внутренней энергией , потому что она
представляет собой сумму кинетической и потенциальной энергий частиц, образующих систему.
Потому что
отсутствие взаимодействия между частицами, единственный вклад во внутреннюю энергию идеального
газа есть кинетическая энергия частиц. Внутренняя энергия идеального газа равна
следовательно, прямо пропорциональна температуре газа.
(В этом уравнении R — постоянная идеального газа, а T — температура
газа в единицах Кельвина.)
Хотя трудно, если вообще возможно, написать уравнение для более сложных
системы, внутренняя энергия системы по-прежнему прямо пропорциональна ее
температура. Поэтому мы можем использовать изменения температуры системы для мониторинга.
Поэтому мы можем использовать изменения температуры системы для мониторинга.
изменение его внутренней энергии.
Величина изменения внутренней энергии системы определяется как
разность между начальным и конечным значениями этой величины.
Е сис
= E окончательная — E начальная
Поскольку внутренняя энергия системы пропорциональна ее температуре, E
положительна при повышении температуры системы.
Первый закон термодинамики: взаимопревращение
тепла и работы
Энергия может передаваться между системой и ее окружением до тех пор, пока энергия
энергия, полученная одним из этих компонентов Вселенной, равна энергии, потерянной
другой.
Е сис
= — E исп.
Энергия может передаваться между системой и ее окружением в виде либо
тепло ( q ) или работа ( w ).
Е сис
= +
Когда тепло поступает в систему, это может привести к повышению температуры системы или
работа.
q = E сис
— с
Правила знаков для связи между внутренней энергией системы и
задано теплоты , пересекающей границу между системой и ее окружением.
на рисунке ниже.
- Когда тепло, поступающее в систему, увеличивает температуру системы, внутренний
энергия системы увеличивается, и E
положительный. - Когда температура системы снижается из-за выхода тепла из системы, E
отрицательно.
Соглашение о знаках для отношения между работой и внутренней энергией
система показана в левой части рисунка ниже.
- Когда система воздействует на окружающую среду, энергия теряется, и E
отрицательно.
- Когда окружающая среда работает над системой, внутренняя энергия системы становится
больше, поэтому E
положительный.
Соотношение между величиной работы, совершаемой системой при ее расширении, и
изменение объема системы ранее описывалось следующим уравнением.
| с | = П В
На приведенном выше рисунке показано, что соглашение о знаках для работы расширения может быть включено
записав это уравнение следующим образом.
w = — P В
Функции состояния
Когда уравнения связывают два или более свойств, описывающих состояние
системы, они называются уравнениями состояния . Например, закон идеального газа
уравнение состояния.
PV = нРТ
Функция состояния s зависит только от состояния системы, а не от
путь, используемый для достижения этого состояния.
Температура является функцией состояния. Сколько бы раз мы ни нагревали, ни охлаждали, ни расширяли,
сжать или иным образом изменить систему, чистое изменение температуры зависит только от
на начальное и конечное состояния системы.
Т
= T окончательная — T начальная
То же самое можно сказать об объеме, давлении и количестве молей газа в
образец. Все эти величины являются функциями состояния.
Теплота и работа являются , а не функциями состояния. Работа не может быть функцией государства, потому что она
пропорциональна расстоянию, на которое перемещается объект, которое зависит от пути, по которому он двигался
от начального до конечного состояния. Если работа не является функцией состояния, то теплота не может быть
государственная функция либо. Согласно первому закону термодинамики изменение
внутренняя энергия системы равна сумме переданной теплоты и работы
между системой и ее окружением.
Е сис
= +
Если Е
зависит не от пути перехода от начального состояния к конечному, а от количества
работы зависит от используемого пути, количество отдаваемой или поглощаемой теплоты должно зависеть
на пути.
Термодинамические свойства системы, являющиеся функциями состояния
обычно обозначаются заглавными буквами ( T , В , Р , Е и так далее
на). Термодинамические свойства, не являющиеся функциями состояния, часто описываются формулой
строчные буквы ( q и w ).
| Практическая задача 3: Что из следующего (а) Температура, T (б) Объем, В (с) Давление, P (d) Количество молей газа, n (e) Внутренняя энергия, E Нажмите |
Измерение тепла с помощью калориметра
Количество теплоты, выделяемой или поглощаемой в ходе химической реакции, можно измерить с помощью
калориметр, как показано на рисунке ниже.
Поскольку реакция происходит в герметичном контейнере при постоянном объеме, никакая работа
расширение происходит во время реакции. Теплота, выделяемая или поглощаемая в результате реакции, равна
равно изменению внутренней энергии системы за время
реакция:
Е сис
= q В .
Количество теплоты, отдаваемое или поглощаемое водой в калориметре, может быть
рассчитывается исходя из теплоемкости воды.
| Практическая задача 4: Природный газ в CH 4 ( г ) + 2 O 2 ( г ) CO 2 ( г ) + 2 H 2 O( г ) Рассчитайте теплоту, выделяющуюся при взаимодействии 0,160 г метана с избытком кислорода в |
 При какой температуре протекает процесс? Чему равно изменение внутренней энергии газа и какую работу совершает газ?
При какой температуре протекает процесс? Чему равно изменение внутренней энергии газа и какую работу совершает газ?
 Чтобы понять, как создается тяга, полезно
Чтобы понять, как создается тяга, полезно

 Линия
Линия