Содержание
Как можно найти силу
Статьи › Школа › Сила Магнита в чем измеряется › Как найти силу в магнитном поле
Связь между массой, силой и ускорением описывается вторым законом Ньютона: СИЛА = МАССА × УСКОРЕНИЕ. 1 ньютон — это сила, которая телу массой 1 кг сообщает ускорение 1 метр в секунду за секунду. Чтобы найти силу тяжести, действующую на тело, надо умножить массу этого тела на ускорение свободного падения 9,8 м/с2.
- Как найти силу по физике
- Как найти силу зная
- Как найти силу через момент
- Как найти F в физике 9 класс
- Как найти F физике
- Как искать силу
- Какой формулой найти силу
- Как определяют силу
- Как измерить какую либо силу
- В чем измеряет силу
- Как рассчитать силу F
- В чем измерить силу
- Как найти силу с помощью работы
Как найти силу по физике
В физике существует множество различных сил, одна из которых — сила тяжести. Она обозначается буквой F и определяется по формуле F=mg. m — это масса тела, а g — ускорение свободного падения. Точка приложения силы всегда находится в центре тела.
Она обозначается буквой F и определяется по формуле F=mg. m — это масса тела, а g — ускорение свободного падения. Точка приложения силы всегда находится в центре тела.
Как найти силу зная
F = P * S. Ответ: чтобы найти силу, нужно умножить давление на площадь поверхности, на которую давит эта сила.
Как найти силу через момент
Модуль момента MO равен произведению модуля силы F на ее плечо h, равное расстоянию от моментной точки О до линии действия силы: MO = F · h.
Как найти F в физике 9 класс
1. F- сила
2. Сумма всех действующих сил равна произведению массы на ускорение
3. Тела действуют друг на друга с силами равными по модулю и противоположными по направлению.
Как найти F физике
F=ma. Формула F=ma выражает второй закон Ньютона, который формулируют так: сила, действующая на тело, равна произведению массы тела на ускорение, сообщаемое этому телу силой.
Как искать силу
Силу, с которой Земля притягивает тела, можно рассчитать по формуле: F = m ⋅ g, где \(m\) — масса тела, а \(g\) — ускорение свободного падения. Ускорение свободного падения — это ускорение, которое вблизи Земли приобретает тело, падающее свободно и беспрепятственно.
Ускорение свободного падения — это ускорение, которое вблизи Земли приобретает тело, падающее свободно и беспрепятственно.
Какой формулой найти силу
M = F × l, где F — модуль силы, l — длина плеча. Единица измерения момента силы в СИ: ньютон-метр (Н·м). Эта формула верна, если сила приложена перпендикулярно оси рычага.
Как определяют силу
А значит, сила, равная одному ньютону, определяется как взаимодействие, которое за 1 секунду изменяет скорость тела массой 1 кг на 1 м/с в направлении действия силы.
Как измерить какую либо силу
Измерить силу можно различными методами: прямым — непосредственно измерить при помощи прибора, например, динамометра; косвенным — рассчитать величину по формуле: F=m*c2 (Сила равна масса умноженная на ускорение в квадрате).
В чем измеряет силу
Размерность силы:
Единицей измерения в СИ является ньютон (русское обозначение: Н; международное: N), в системе СГС — дина (русское обозначение: дин, международное: dyn).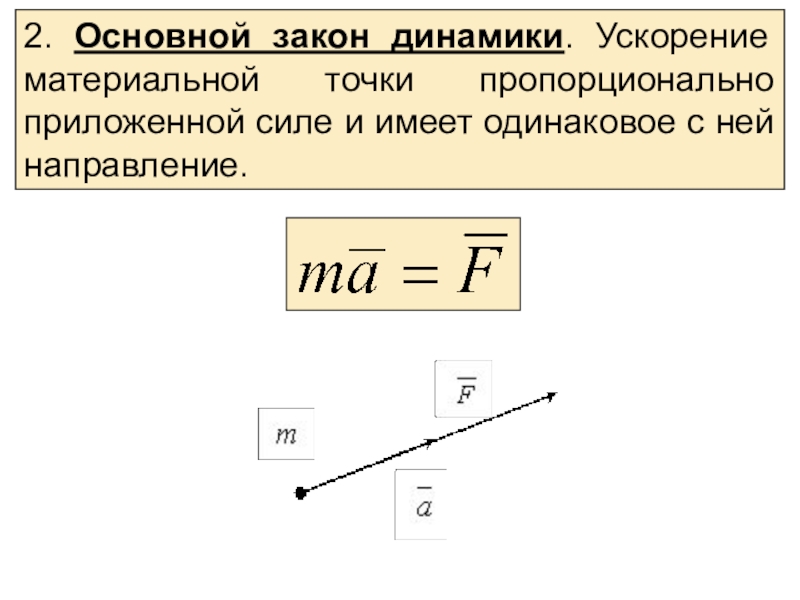
Как рассчитать силу F
Формула силы. По второму закону Ньютона F = m х a означает, что, если к массе m приложить силу F, то тело будет двигаться с скоростью, которая имеет ускорение а.
В чем измерить силу
Единицей измерения в СИ является ньютон (русское обозначение: Н; международное: N), в системе СГС — дина (русское обозначение: дин, международное: dyn).
Как найти силу с помощью работы
A = Fs, где А — работа, F — сила и s — пройденный путь. За единицу работы принимается работа, совершаемая силой в 1Н, на пути, равном 1 м. Единица работы — джоуль (Дж) названа в честь английского ученого Джоуля.
Ускорение свободного падения — формулы, примеры и определение
Покажем, как применять знание физики в жизни
Начать учиться
Чем отличается яблоко, упавшее в Алматы, от такого же яблока в Осло? Тем, что в этих городах разное ускорение свободного падения! Что это такое и как его вычислить — отвечаем в статье.
Сила тяготения
В 1682 году Исаак Ньютон открыл закон всемирного тяготения. Он звучит так: все тела притягиваются друг к другу с силой, которая прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.
Формула силы тяготения согласно этому закону выглядит так:
Закон всемирного тяготения F — сила тяготения [Н] M — масса первого тела (часто планеты) [кг] m — масса второго тела [кг] R — расстояние между телами [м] G — гравитационная постоянная G = 6,67 · 10−11м3 · кг−1 · с−2 |
Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.
Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.
Закон всемирного тяготения используют, чтобы вычислить силы взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними.
Если мы возьмем два шара, то для них можно использовать этот закон вне зависимости от расстояния между ними. За расстояние R между телами в этом случае принимается расстояние между центрами шаров.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Ускорение свободного падения
Чтобы математически верно и красиво прийти к ускорению свободного падения, нам необходимо сначала ввести понятие силы тяжести.
Сила тяжести — сила, с которой Земля притягивает все тела.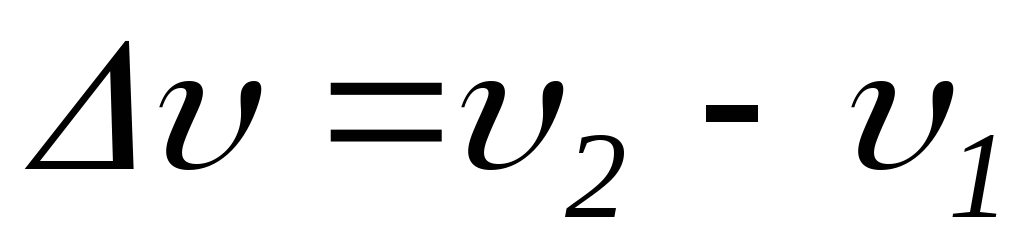
Сила тяжести F = mg F — сила тяжести [Н] m — масса тела [кг] g — ускорение свободного падения [м/с2] На планете Земля g = 9,8 м/с2, но подробнее об этом чуть позже. 😉 |
На первый взгляд сила тяжести очень похожа на вес тела. Действительно, в состоянии покоя на поверхности Земли формулы силы тяжести и веса идентичны. Вес тела в состоянии покоя численно равен массе тела, умноженной на ускорение свободного падения, разница состоит лишь в точке приложения силы.
Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору или подвес. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.
Также важно понимать, что сила тяжести зависит исключительно от массы и планеты, на которой тело находится. А вес зависит еще и от ускорения, с которым движется тело или опора.
Например, в лифте вес зависит от того, куда и с каким ускорением двигаются его пассажиры. А силе тяжести все равно, куда и что движется — она не зависит от внешних факторов.
На второй взгляд сила тяжести очень похожа на силу тяготения. В обоих случаях мы имеем дело с притяжением — значит, можем сказать, что это одно и то же. Практически.
Мы можем сказать, что это одно и то же, если речь идет о Земле и каком-то предмете, который к этой планете притягивается.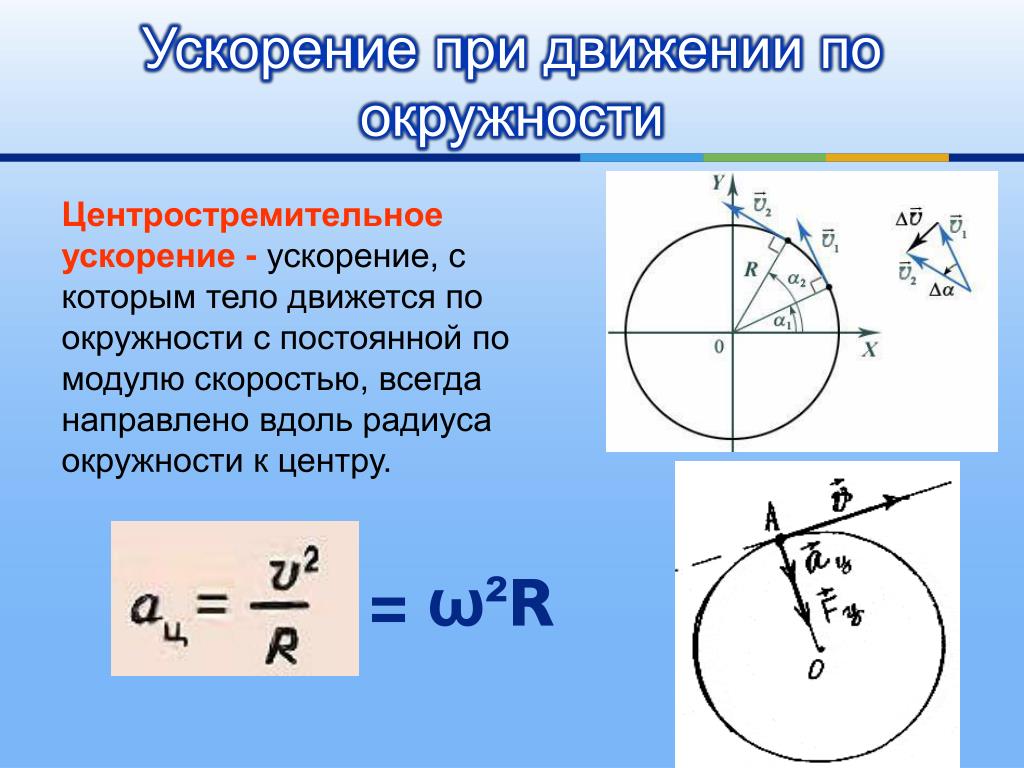 Тогда мы можем даже приравнять эти силы и выразить формулу для ускорения свободного падения:
Тогда мы можем даже приравнять эти силы и выразить формулу для ускорения свободного падения:
Приравниваем правые части:
Делим на массу тела левую и правую части:
Это и будет формула ускорения свободного падения. Ускорение свободного падения для каждой планеты уникально.
Формула ускорения свободного падения g — ускорение свободного падения [м/с2] M — масса планеты [кг] R — расстояние между телами [м] G — гравитационная постоянная G = 6,67 · 10−11м3 · кг−1 · с−2 |
Ускорение свободного падения характеризует то, как быстро увеличивается скорость тела при свободном падении.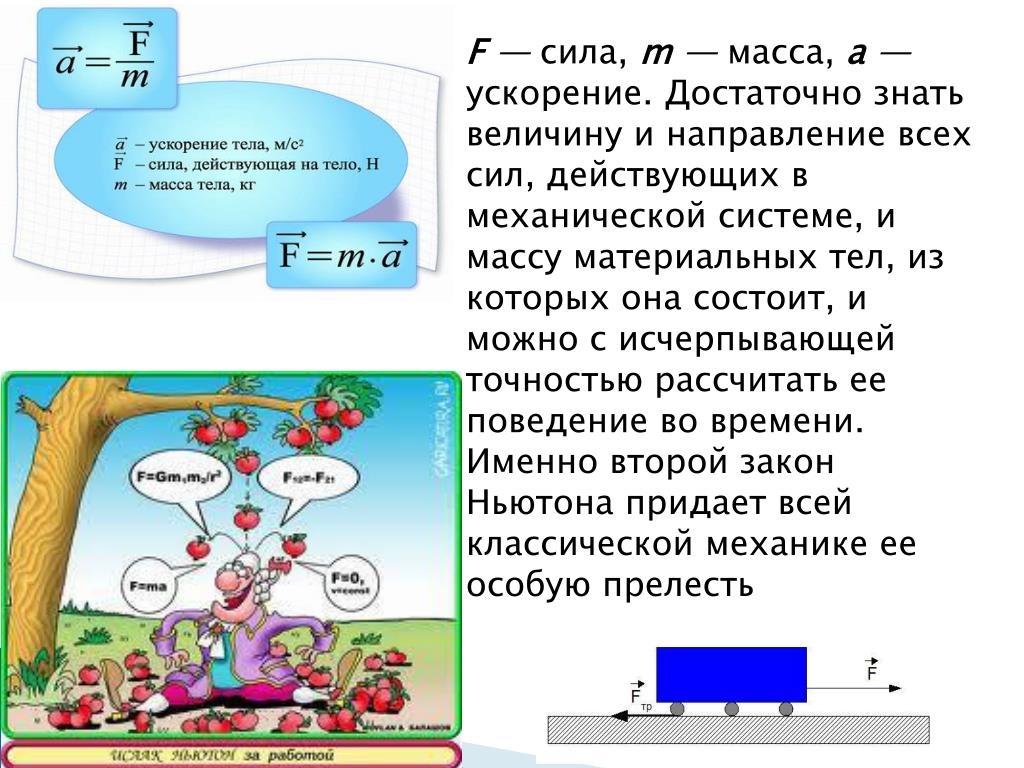
Свободное падение — это ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести.
Ускорение свободного падения на разных планетах
Выше мы уже вывели формулу ускорения свободного падения. Давайте попробуем рассчитать ускорение свободного падения на планете Земля.
Для этого нам понадобятся следующие величины:
- Гравитационная постоянная
G = 6,67 · 10−11м3 · кг−1 · с−2 - Масса Земли
M = 5,97 × 1024 кг - Радиус Земли
R = 6371 км
Подставим значения в формулу:
Есть один нюанс: в значении ускорения свободного падения для Земли очень много знаков после запятой.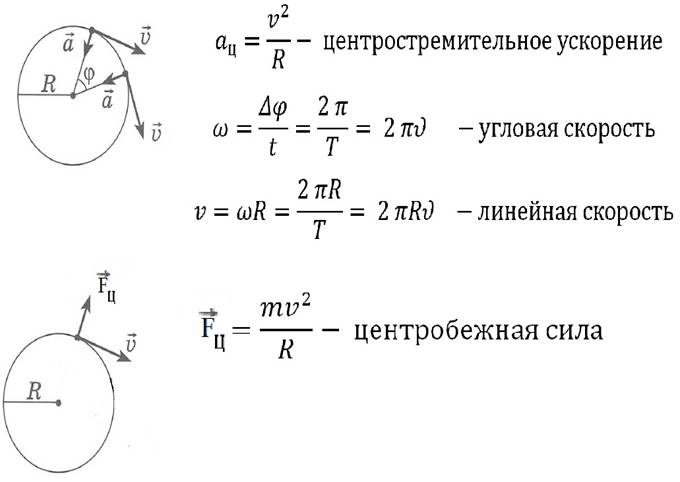 В школе обычно дают то же значение, что мы указали выше: g = 9,81 м/с2. В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с2.
В школе обычно дают то же значение, что мы указали выше: g = 9,81 м/с2. В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с2.
И кому же верить?
Все просто: для кого решается задача, тот и главный. В экзаменах берем g = 10 м/с2, в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8 м/с2.
Ниже представлена таблица ускорений свободного падения и других характеристик для планет Солнечной системы, карликовых планет и Солнца.
Небесное тело | Ускорение свободного падения, м/с2 | Диаметр, км | Расстояние до Солнца, миллионы км | Масса, кг | Соотношение с массой Земли |
|---|---|---|---|---|---|
Меркурий | 3,7 | 4 878 | 58 | 3,3×1023 | 0,055 |
Венера | 8,87 | 12 103 | 108 | 4,9×1024 | 0,82 |
Земля | 9,8 | 12 756,28 | 150 | 6,0×1024 | 1 |
Марс | 3,7 | 6 794 | 228 | 6,4×1023 | 0,11 |
Юпитер | 24,8 | 142 984 | 778 | 1,9×1027 | 317,8 |
Сатурн | 10,4 | 120 536 | 1 427 | 5,7×1026 | 95,0 |
Уран | 8,87 | 51 118 | 2 871 | 8,7×1025 | 14,4 |
Нептун | 10,15 | 49 532 | 4 498 | 1,02×1026 | 17,1 |
Плутон | 0,66 | 2 390 | 5 906 | 1,3×1022 | 0,0022 |
Луна | 1,62 | 3 473,8 | 0,3844 (до Земли) | 7,35×1022 | 0,0123 |
Солнце | 274,0 | 1 391 000 | 0 | 2,0×1030 | 332 900 |
Ускорение свободного падения на Земле в разных местах
Сюрприз-сюрприз! В разных городах ускорения свободного падения тоже различаются. Это происходит из-за того, что Земля имеет форму геоида — приплюснутого шара, и в разных точках у нее различается радиус. Если подставить эти радиусы в формулу ускорения свободного падения, получатся разные значения. Ниже представлены некоторые из них.
Это происходит из-за того, что Земля имеет форму геоида — приплюснутого шара, и в разных точках у нее различается радиус. Если подставить эти радиусы в формулу ускорения свободного падения, получатся разные значения. Ниже представлены некоторые из них.
Ускорение свободного падения для некоторых городов | ||||
|---|---|---|---|---|
Город | Долгота | Широта | Высота над уровнем моря, м | Ускорение свободного падения, м/с2 |
Алматы | 76,85 в. д. | 43,22 с. | 786 | 9,78125 |
Берлин | 13,40 в. д. | 52,50 с. ш. | 40 | 9,81280 |
Будапешт | 19,06 в. д. | 47,48 с. ш. | 108 | 9,80852 |
Вашингтон | 77,01 з. д. | 38,89 с. ш. | 14 | 9,80188 |
Вена | 16,36 в. | 48,21 с. ш. | 183 | 9,80860 |
Владивосток | 131,53 в. д. | 43,06 с. ш. | 50 | 9,80424 |
Гринвич | 0,0 в. д. | 51,48 с. ш. | 48 | 9,81188 |
Каир | 31,28 в. д. | 30,07 с. | 30 | 9,79317 |
Киев | 30,30 в. д. | 50,27 с. ш. | 179 | 9,81054 |
Мадрид | 3,69 в. д. | 40,41 с. ш. | 667 | 9,79981 |
Минск | 27,55 в. д. | 53,92 с. ш. | 220 | 9,81347 |
Москва | 37,61 в. | 55,75 с. ш. | 151 | 9,8154 |
Нью-Йорк | 73,96 з. д. | 40,81 с. ш. | 38 | 9,80247 |
Одесса | 30,73 в. д. | 46,47 с. ш. | 54 | 9,80735 |
Осло | 10,72 в. д. | 59,91 с. | 28 | 9,81927 |
Париж | 2,34 в. д. | 48,84 с. ш. | 61 | 9,80943 |
Прага | 14,39 в. д. | 50,09 с. ш. | 297 | 9,81014 |
Рим | 12,99 в. д. | 41,54 с. ш. | 37 | 9,80312 |
Стокгольм | 18,06 в. | 59,34 с. ш. | 45 | 9,81843 |
Токио | 139,80 в. д. | 35,71 с. ш. | 18 | 9,79801 |
Например, ускорение свободного падения в Алматы меньше, чем в Осло. Значит, если два яблока упадут с одинаковой высоты в этих городах, то к концу падения яблоко в Осло наберет большую скорость, чем яблоко в Алматы.
Но разве это не зависит еще и от массы предмета?
Нет, не зависит. На самом деле все тела падают одинаково вне зависимости от массы. Если мы возьмем перо и мяч, то перо, конечно, будет падать медленнее, но не из-за ускорения свободного падения.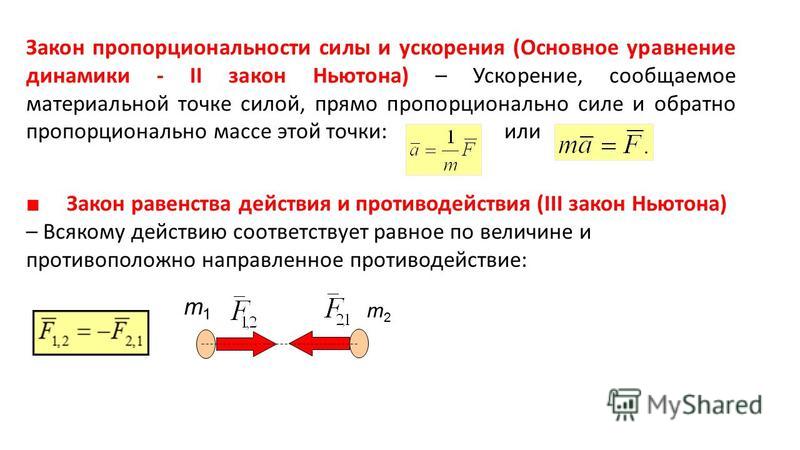 Просто из-за небольшой массы пера сопротивление воздуха оказывает на него большее воздействие, чем на мяч. А вот если бы мы поместили перо и мяч в вакуум, они бы упали одновременно.
Просто из-за небольшой массы пера сопротивление воздуха оказывает на него большее воздействие, чем на мяч. А вот если бы мы поместили перо и мяч в вакуум, они бы упали одновременно.
Уроки физики в онлайн-школе Skysmart не менее увлекательны, чем наши статьи!
Карина Хачатурян
К предыдущей статье
Электроемкость конденсатора
К следующей статье
Удельная теплота сгорания
Получите индивидуальный план обучения физике на бесплатном вводном уроке
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Нахождение ускорения
Как уже говорилось ранее в уроке 3 (а также в уроке 2), результирующая сила представляет собой векторную сумму всех отдельных сил.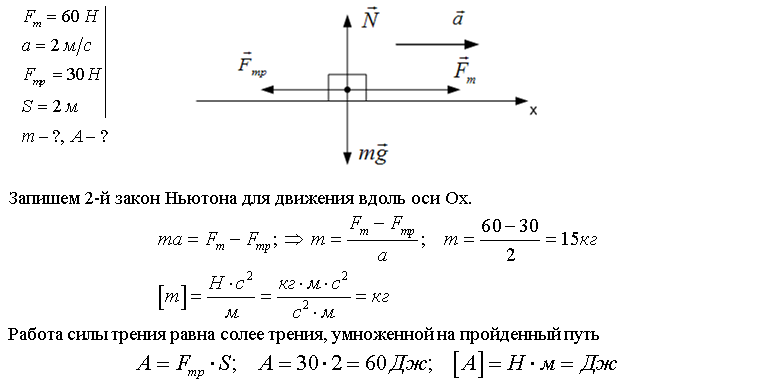 На уроке 2 мы узнали, как определить результирующую силу, если известны величины всех отдельных сил. На этом уроке мы научимся определять ускорение объекта, если известны величины всех отдельных сил. Три основных уравнения, которые будут полезны, — это уравнение для общей силы (F net = m•a), уравнение для гравитационной силы (F грав = м•г), и уравнение для силы трения (F трение = μ • F норма ).
На уроке 2 мы узнали, как определить результирующую силу, если известны величины всех отдельных сил. На этом уроке мы научимся определять ускорение объекта, если известны величины всех отдельных сил. Три основных уравнения, которые будут полезны, — это уравнение для общей силы (F net = m•a), уравнение для гравитационной силы (F грав = м•г), и уравнение для силы трения (F трение = μ • F норма ).
Процесс определения ускорения объекта требует, чтобы были известны масса и результирующая сила. Если масса (м) и результирующая сила (F net ) известны, то ускорение определяется с помощью уравнения.
Ваш переход к практике ускорение. Чтобы почувствовать, как применяется этот метод, попробуйте решить следующие практические задачи. После того, как вы решили задачи, нажмите кнопку, чтобы проверить свои ответы.
Практика №1
Приложенная сила в 50 Н используется для ускорения объекта вправо по поверхности трения.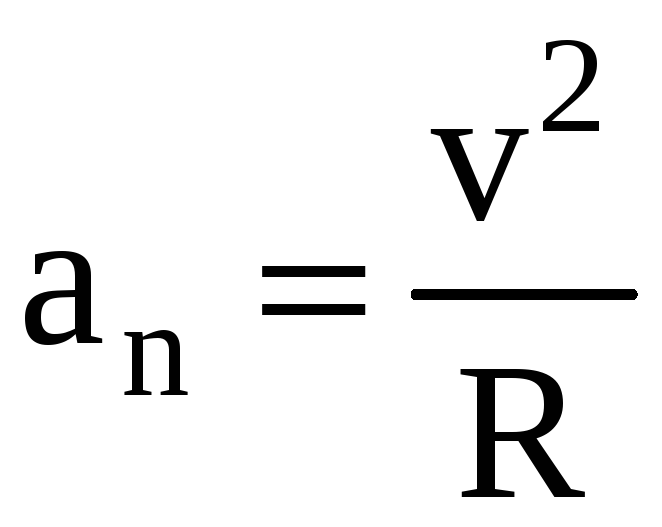 Объект сталкивается с силой трения 10 Н. Используйте диаграмму, чтобы определить нормальную силу, результирующую силу, массу и ускорение объекта. (Сопротивлением воздуха пренебречь.)
Объект сталкивается с силой трения 10 Н. Используйте диаграмму, чтобы определить нормальную силу, результирующую силу, массу и ускорение объекта. (Сопротивлением воздуха пренебречь.)
Практика №2
Приложенная сила в 20 Н используется для ускорения объекта вправо по поверхности трения. Объект сталкивается с силой трения 10 Н. Используйте диаграмму, чтобы определить нормальную силу, результирующую силу, коэффициент трения (μ) между объектом и поверхностью, массу и ускорение объекта. (Сопротивлением воздуха пренебречь.)
Практика №3
Объект массой 5 кг скользит вправо и сталкивается с силой трения, которая замедляет его. Коэффициент трения (μ) между объектом и поверхностью равен 0,1. Определить силу тяжести, нормальную силу, силу трения, результирующую силу и ускорение. (Сопротивлением воздуха пренебречь.)
Определить силу тяжести, нормальную силу, силу трения, результирующую силу и ускорение. (Сопротивлением воздуха пренебречь.)
Ниже приведены еще несколько практических задач. Вы должны приложить усилия, чтобы решить как можно больше задач без помощи заметок, решений, учителей и других учеников. Посвятите себя индивидуальному решению проблем. Между тем, стоит упомянуть важное предостережение:
Избегайте форсирования проблемы в виде ранее решенной проблемы. Проблемы в физике редко выглядят одинаково. Вместо решения проблем наизусть или путем имитации ранее решенной проблемы, используйте свое концептуальное понимание законов Ньютона для поиска решений проблем. Используйте свое понимание веса и массы, чтобы найти m или Fgrav в задаче. Используйте свое концептуальное понимание чистой силы ( векторная сумма всех сил ), чтобы найти значение Fnet или значение отдельной силы.
Не отделяйте решение физических задач от понимания физических концепций. Если вы не можете решить физические задачи, подобные приведенным выше, это не обязательно означает, что у вас проблемы с математикой. Вполне вероятно, что у вас возникли трудности с понятиями физики.
Мы хотели бы предложить …
Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Force Interactive. Вы можете найти его в разделе Physics Interactives на нашем сайте. Force Interactive позволяет учащимся исследовать влияние изменений приложенной силы, результирующей силы, массы и трения на ускорение объекта.
Посетите: Force
Проверьте свое понимание
1. Эдвардо прикладывает направленную вправо силу 4,25 Н к книге весом 0,765 кг, чтобы ускорить ее перемещение по поверхности стола. Коэффициент трения между книгой и столешницей равен 0,410. Определить ускорение книги.
Эдвардо прикладывает направленную вправо силу 4,25 Н к книге весом 0,765 кг, чтобы ускорить ее перемещение по поверхности стола. Коэффициент трения между книгой и столешницей равен 0,410. Определить ускорение книги.
2. В физической лаборатории Кейт и Роб используют подвесную массу и систему шкивов, чтобы приложить направленную вправо силу 2,45 Н к тележке массой 0,500 кг, чтобы ускорить ее движение по дорожке с низким коэффициентом трения. Если полная сила сопротивления движению тележки равна 0,72 Н, то чему равно ускорение тележки?
Следующий раздел:
Перейти к следующему уроку:
Ускорение: определение, формула и единицы измерения
Всякий раз, когда мы рассматриваем движение движущегося объекта, редко бывает, что скорость остается постоянной на всем протяжении его движения. Скорость объектов обычно увеличивается и уменьшается в зависимости от их траектории. Ускорение — это слово, используемое для обозначения скорости изменения скорости, и это мера скорости, с которой скорость объекта увеличивается или уменьшается. Это называется ускорением. Он используется во многих важных расчетах, например, при проектировании тормозной системы транспортного средства и т. Д. В этой статье мы рассмотрим различные уравнения, которые используются при расчете ускорения тела. Мы также рассмотрим несколько примеров из реальной жизни, где используются уравнения.
Ускорение — это слово, используемое для обозначения скорости изменения скорости, и это мера скорости, с которой скорость объекта увеличивается или уменьшается. Это называется ускорением. Он используется во многих важных расчетах, например, при проектировании тормозной системы транспортного средства и т. Д. В этой статье мы рассмотрим различные уравнения, которые используются при расчете ускорения тела. Мы также рассмотрим несколько примеров из реальной жизни, где используются уравнения.
- Определение ускорения
- Единицы ускорения
- Вектор ускорения
- График скорости и времени ускорения
- Формула ускорения
- Ускорение под действием силы тяжести
Определение ускорения
Ускорение – это скорость изменения скорости относительно time
Мы можем рассчитать ускорение, если знаем, насколько изменится скорость объекта за определенный период времени при условии, что он движется по прямой линии с постоянным ускорением.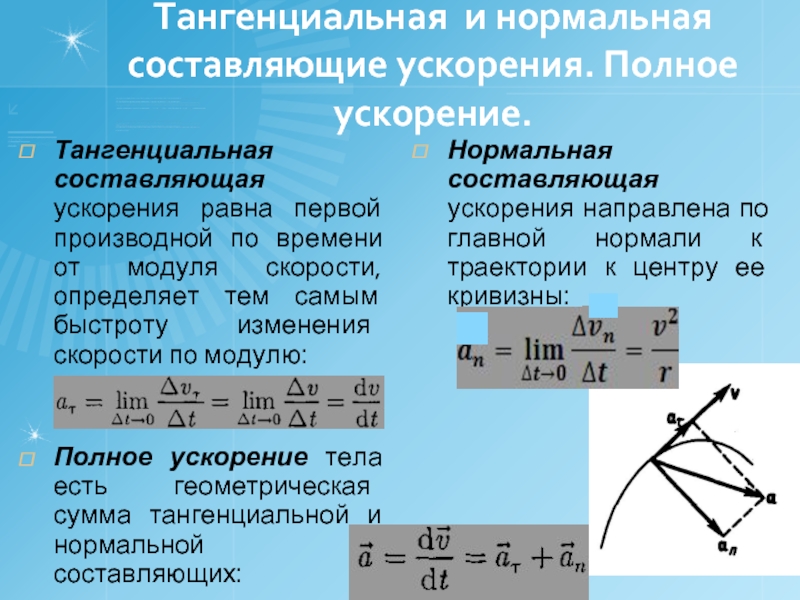 Это дается следующим уравнением 92\). Ускорение может быть отрицательным или положительным. Отрицательное ускорение называется замедлением.
Это дается следующим уравнением 92\). Ускорение может быть отрицательным или положительным. Отрицательное ускорение называется замедлением.
Вектор ускорения
Ускорение \(\vec{a}\) является векторной величиной. Это также потому, что он получен из вектора скорости \(\vec{v}\). Глядя на уравнение для вектора ускорения, мы видим, что оно прямо пропорционально изменению скорости и обратно пропорционально времени, необходимому для ускорения или замедления. На самом деле, мы можем получить представление о направлении вектора ускорения, взглянув на величину вектора скорости.
Если скорость объекта увеличивается (начальная скорость < конечной скорости) , то он имеет положительное ускорение в направлении скорости.
Если скорость уменьшается, (\(u>v\)) то ускорение отрицательное и в направлении, противоположном скорости.

Если скорость постоянна (\(u=v\)) то ускорение равно \(0\). Почему вы так думаете? Это происходит потому, что ускорение определяется изменением скорости. Давайте визуализируем эту связь с помощью графиков.
\[a=\dfrac{v-u}{t},\quad\text{if}\quad v-u=0,\quad\text{then}\quad a=0\]
Скорость и время ускорения graphs
Скорость и ускорение движущегося объекта можно визуализировать с помощью графика времени. На приведенном ниже графике показан график зависимости скорости от времени объекта, движущегося по прямой линии.
График зависимости скорости от времени с тремя участками, соответствующими ускорению, постоянной скорости и замедлению, Kids Brittanica
Оранжевая линия показывает, что скорость увеличивается во времени, это означает, что объект имеет положительное ускорение.

Зеленая линия параллельна, что означает, что скорость постоянна, что означает, что ускорение равно нулю.
Синяя линия представляет собой наклон вниз, показывающий снижение скорости, что указывает на отрицательное замедление.
Чтобы рассчитать ускорение в любой точке, нам нужно найти наклон кривой скорости.
\[\text{slope}=\dfrac{y_2-y_1}{x_2-x_1}\]
где \((x_1,y_1)\) — координаты начальной точки на графике и \ ((x_2,y_2)\) — координаты конечной точки. Мы знаем, что ось Y записывает скорость, а ось X записывает затраченное время, это означает, что формула не что иное, как:
\[a=\dfrac{v-u}{t}\]
Давайте рассмотрим это в качестве примера.
Найдите ускорение объекта по приведенному выше графику скорость-время для начальных \(10\) секунд.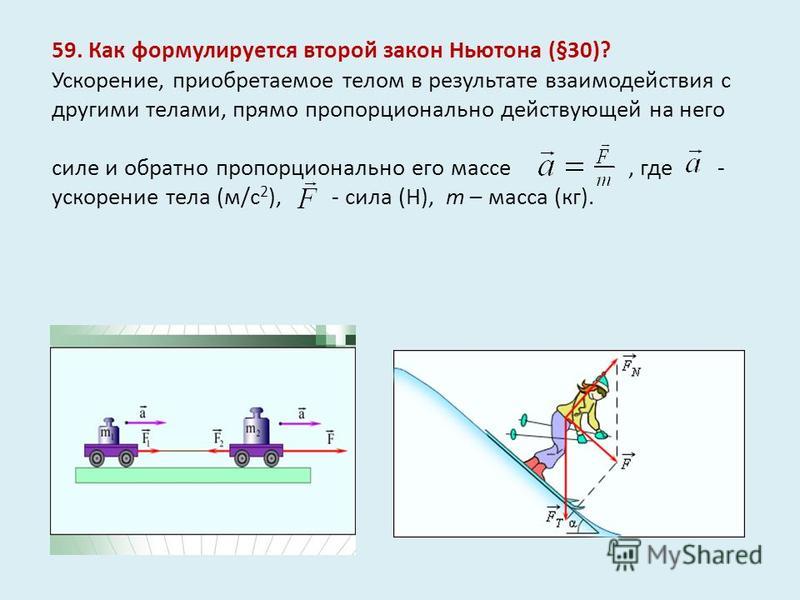 2\конец{выравнивание}\] 92)\).
2\конец{выравнивание}\] 92)\).
Формула ускорения
Теперь мы знаем некоторые соотношения между ускорением, скоростью и временем. Но можно ли напрямую связать пройденное расстояние с ускорением? Предположим, что объект находится в состоянии покоя (начальная скорость \(u=0\)) и затем ускоряется до конечной скорости \(v\) за время \(t\). Средняя скорость определяется выражением
\[v_{\text{average}}=\dfrac{s}{t}\]
Преобразовывая уравнение для расстояния \(s\), мы получаем
\[ с = v _ {\ текст {среднее}} т \]
Ускорение объекта равно \(\dfrac{v-0}{t}\), так как оно стартовало из состояния покоя \((u=0)\).
\[a=\dfrac{v}{t}\]
Переставляя по \(v\) получаем
\[v=at\]
Задана средняя скорость объекта by
\[v_{\text{average}}=\dfrac{v+u}{2}=\dfrac{v_f}{2}\]
Подставьте среднюю скорость в приведенное выше уравнение, и мы получим
\[v_{\text{average}}=2at\]
Наконец, подставьте это в уравнение для расстояния, и мы получим 92\]
Вот оно, уравнение, напрямую связывающее ускорение и перемещение. Но что, если объект не начал двигаться из состояния покоя? т. е. \(v_i\) не равно \(0\). Давайте разберемся. Ускорение теперь равно
Но что, если объект не начал двигаться из состояния покоя? т. е. \(v_i\) не равно \(0\). Давайте разберемся. Ускорение теперь равно
\[a=\dfrac{v-u}{t}\]
Переставляем конечную скорость \(v\), и получаем,
\[v=u+at\]
Средняя скорость изменится на
\[a_{\text{average}}=\dfrac{u+v}{2}\]
Подставьте значение конечной скорости в приведенное выше уравнение 92\). К сожалению, у нас есть последнее уравнение, которое относится к ускорению и скорости в целом. Насколько это интересно? Вот как это работает; во-первых, вы переписываете уравнение для ускорения относительно времени:
\[t=\dfrac{v-u}{a}\]
Теперь смещение,
\[s=v_{\text{average}}t \]
Средняя скорость при постоянном ускорении равна
\[v_{\text{average}}=\dfrac{1}{2}(v+u)\]
\text{average}}\) в уравнении для \(s\) и получаем 92\times 40\,\mathrm{m}}{3\,\mathrm{s}/\mathrm{s}\times 3\,\mathrm{m}/\mathrm{s}}}\\v&=4,21 \,\mathrm{m}/\mathrm{s}\end{align}\]
Конечная скорость автомобиля равна \(4. 21\,\mathrm{m}/\mathrm{s}\).
21\,\mathrm{m}/\mathrm{s}\).
Ускорение под действием силы тяжести
Ускорение под действием силы тяжести, представленное \(g\), представляет собой ускорение объекта при свободном падении под действием силы тяжести, действующей на него. Это ускорение под действием силы тяжести зависит от гравитационной силы планеты. Следовательно, она будет меняться для разных планет. Стандартным значением \(g\) на Земле считается \(92\). Что это значит? Это означает, что свободно падающий объект будет ускоряться со значением \(g\), продолжая падать на землю.
Значение \(g\), как мы знаем, является постоянным, но на самом деле оно меняется из-за множества факторов. На значение \(g\) влияет глубина или высота над уровнем моря. Значение \(g\) уменьшается по мере увеличения глубины объекта. На это также может повлиять его положение на Земле. Величина \(g\) больше на экваторе, чем на полюсах. И, наконец, на эту величину также влияет вращение Земли. 92\).

 ш.
ш. д.
д. ш.
ш. д.
д. ш.
ш. д.
д. Не отделяйте решение физических задач от понимания физических концепций. Если вы не можете решить физические задачи, подобные приведенным выше, это не обязательно означает, что у вас проблемы с математикой. Вполне вероятно, что у вас возникли трудности с понятиями физики.
Не отделяйте решение физических задач от понимания физических концепций. Если вы не можете решить физические задачи, подобные приведенным выше, это не обязательно означает, что у вас проблемы с математикой. Вполне вероятно, что у вас возникли трудности с понятиями физики.
