Содержание
1.2. Виды понятий. Логическая характеристика по объему и содержанию
1.
По объему понятия делятся на единичные
и общие.
Единичным
является понятие, объем которого состоит
из одно-
го
элемента. Например, понятия
«Александр Сергеевич Пушкин»,
«созвездие
Большой Медведицы», «эта книга» и др.
Общие
понятия имеют в качестве объема класс,
состоящий бо-
лее
чем из одного элемента. Например:
«человек», «животное» и др.
2.
Общие понятия, в свою очередь, делятся
на регистрирую-
щие
и нерегистрирующие.
Регистрирующие
– это такие понятия, объем которых
состав-
ляет
конечное множество элементов, в принципе
поддающихся учету.
Например,
«планеты Солнечной системы», «человек»,
«следователь».
Нерегистрирующие
– такие понятия, объем которых составля-
ет бесконечное множество элементов и
не поддается принципиально- му учету.
Например, «число», «атом», «молекула».
3.
Понятия делятся на разделительные и
собирательные.
Разделительные
понятия – такие понятия, в объеме которых
каждый индивидуальный предмет мыслится
как элемент класса. На- пример, «книга»,
«человек», «звезда».
Собирательные
– такие понятия, в которых предметы
мыслят-
ся
как единое целое. Например, «человечество»,
«созвездие», «флот».
4.
По
содержанию
понятия делятся на конкретные и абст-
рактные.
Конкретными
называются понятия, в которых мыслятся
пред-
меты
в совокупности своих признаков.
Например, «стол», «стул»,
«человек»,
«дерево» и т. д.
Абстрактными
называются понятия, в которых мыслятся
свойства или отношения, отвлеченные от
самих предметов: «счастье»,
«белизна»,
«бесконечность».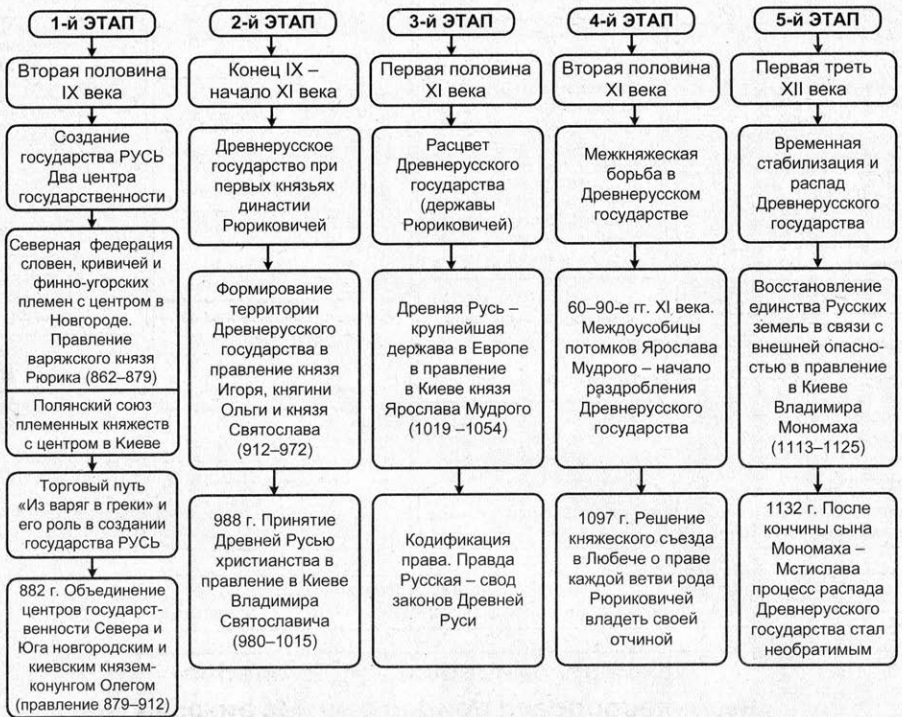
5.
Понятия бывают положительные и
отрицательные.
Положительными
называются понятия, которые выражают
наличие у предмета какого-либо свойства
или отношения. Например,
«преступник»,
«европейское государство», «столичный
город».
Отрицательными
называются такие понятия, в которых
ука- зывается на отсутствие какого-либо
свойства или отношения Напри- мер,
«не-преступник», «неевропейское
государство», «нестоличный
город».
ных
посредством прибавления к положительным
понятиям отрица- тельной частицы «не»
или приставки «без». Однако следует
помнить, что в случаях, когда без
отрицательной частицы понятие не
употреб- ляется, оно является положительным.
Например, «неряха», «нена- стье» и т. д.
6.
По содержанию понятия делятся также на
соотноситель-
ные
и безотносительные.
Соотносительными
считаются такие понятия, в которых от-
ражаются предметы, существование одного
из которых немыслимо без существования
другого, например, «дети» и «родители»,
«началь-
ник»
и «подчиненный», «верх» и «низ» и т. д.
д.
Безотносительные
– такие понятия, в которых отражаются
предметы, существование которых не
связывается необходимым об- разом
с существованием других
предметов. Например, «человек»,
«книга»,
«парта» и т. д.
|
Для
удобства все указанные виды понятий
можно представить на общей схеме:
Таким
образом, определить, к какому виду
относится то или иное понятие – значит
дать его логическую характеристику.
В
современной логике принято делить
понятия на: ясные и размытые; единичные
и общие; собирательные и несобирательные;
конкретные и абстрактные; положительные
и отрицательные; безотносительные и
соотносительные. Перейдем к рассмотрению
каждого вида понятий отдельно.
Ясные
и размытые. В зависимости от содержания
понятий они могут отражать действительность
более или менее точно. Именно это качество
положено в основу разделения понятий
на ясные и размытые. Как несложно
догадаться, четкость отражения значительно
выше у ясных понятий, размытые же нередко
отражают предмет с недостаточной
полнотой. Например, ясное понятие
«инфляция» содержит в своих характеристиках
достаточно четкое указание на степень
экономической дестабилизации в стране.
В
разных отраслях науки (в основном
гуманитарных) используются понятия с
размытым содержанием (перестройка,
гласность), что зачастую носит негативный
характер. Особенно это характерно для
правоприменительной деятельности, в
процессе которой недостаточная
определенность правовых норм может
приводить к их свободному толкованию
субъектами права. Очевидно, что это
недопустимо.
Единичные
и общие понятия. Такое разделение
связано с тем, подразумевается ли в них
один элемент или же несколько.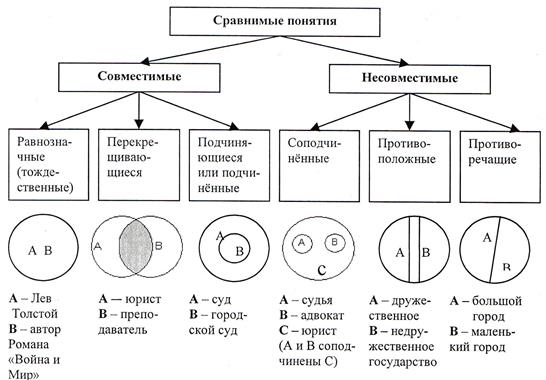 Как
Как
нетрудно догадаться, понятия, в которых
подразумевается лишь один элемент,
называются единичными (например,
«Венеция», «Дж. Лондон», «Париж»). Понятия
же, в которых мыслится несколько
элементов, называются общими (например,
«страна», «писатель», «столица»).
Общие
понятия могут быть регистрирующими
и нерегистрирующими. Отличаются они
тем, что в регистрирующих понятиях
множество подразумеваемых элементов
поддается учету, может быть зафиксировано.
Нерегистрирующие понятия характеризуются
тем, что множество их элементов не
поддается учету, они имеют бесконечный
объем.
Понятия
собирательные и несобирательные. Понятия,
содержащие признаки некоторой совокупности
элементов, входящих в один комплекс,
принято называть собирательными. В
качестве примера собирательных понятий
можно привести понятия «команда»,
«стая», «отряд». Необходимо отметить,
что содержание единичного понятия
нельзя относить к отдельному элементу,
входящему в его объем, так как оно
относится сразу ко всем элементам.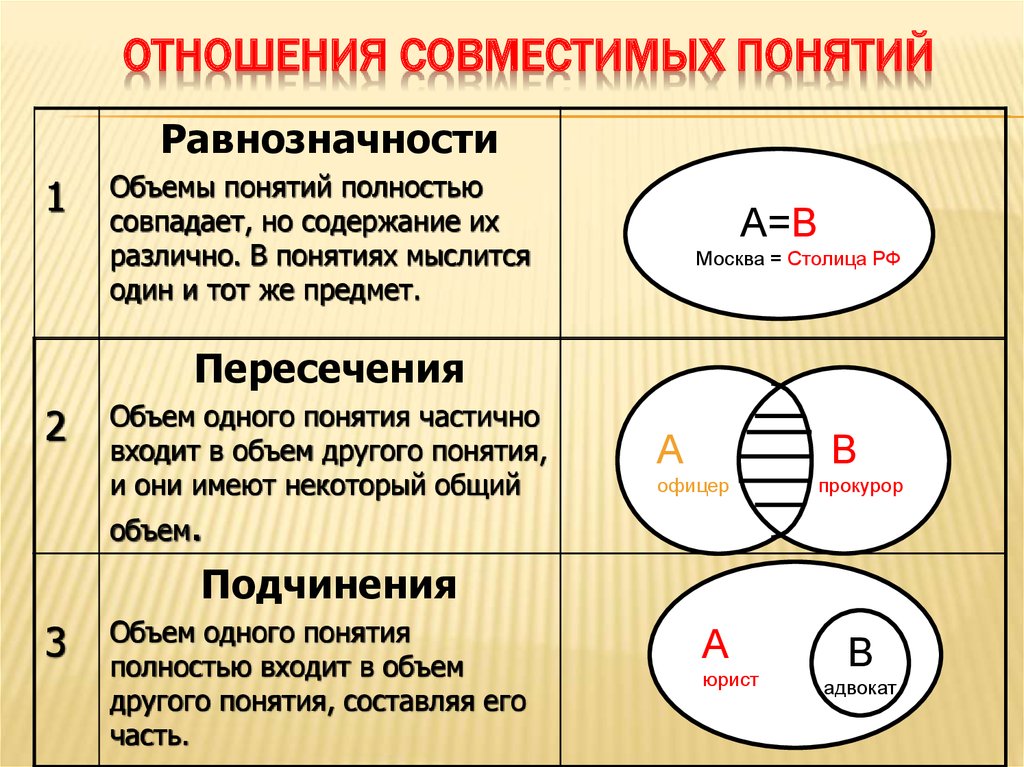
Собирательные понятия бывают общими («команда»,
«стая») и единичными («команда
„Сокол“», «отряд „Альфа“»).
Понятия,
содержащие признаки не целой совокупности,
а отдельных элементов,
называются несобирательными. Если
употребление в речи такого понятия
относится к каждому из элементов,
составляющих его объем, такое выражение
именуют разделительным. Если же
упоминаются все элементы в комплексе
(совокупности) и безотносительно к
каждому из элементов, взятому в
отдельности, такое выражение
называют собирательным.
Конкретные
и абстрактные понятия. Такое разделение
понятий зависит от предмета, отражаемого
в содержании понятия. Это может быть
предмет, или некая совокупность предметов,
или признак этого предмета (отношение
между предметами). Соответственно
понятие, содержание которого составляет
информация о признаке предмета или
отношение между предметами,
именуется абстрактным понятием. Напротив,
понятие о предмете или совокупности
предметов называется конкретным.
Главным
признаком, чертой, по которой проводится
разделение понятий на конкретные и
абстрактные, является соотношение
предмета и его признаков. Иными словами,
хотя признаки предмета и не могут
существовать без последнего, в результате
логического приема «абстрагирование»
они выделяются в самостоятельный объект
мысли и рассматриваются безотносительно
своего предмета. Соответственно и
понятие носит название абстрактного.
Нельзя
забывать о том, что конкретные и единичные
понятия не являются синонимами, также
как и абстрактные необходимо отделять
от общих. Так, общие
понятия могут
быть и конкретными, и абстрактными.
Например, понятие «купец» является
общим и конкретным, а понятие
«посредничество» – общим и абстрактным.
Положительные
и отрицательные понятия. В основу
классифицирования данных понятий
положены свойства предмета, явления
или процесса. Вид понятия здесь поставлен
в зависимость от наличия либо отсутствия
у предмета характеризующих свойств.
Говоря иначе, понятие именуется
положительным, если в нем содержится
указание на наличие свойств, присущих
предмету. В противоположность положительным
выступают отрицательные понятия, которые
подразумевают отсутствие таких свойств.
Так, положительным понятием будет
«сильный», а отрицательным – «слабый»;
положительным – «спокойный», отрицательным
– «беспокойный».
Безотносительные
и соотносительные понятия. В основу
этой классификации положено наличие
либо отсутствие связи предмета,
составляющего объем понятия, с другими
предметами материального мира. Таким
образом, безотносительными будут
понятия, существующие отдельно друг от
друга и не оказывающие на существование
каждого из них существенного влияния.
Такими понятиями, например, могут быть
«гвоздь» и «пуговица». Каждый из этих
предметов существует отдельно и
независимо от другого.
Отталкиваясь
от сказанного выше, можно определить
соотносительные понятия как имеющие
связь друг с другом, заложенную в
признаках предметов, составляющих их
объем.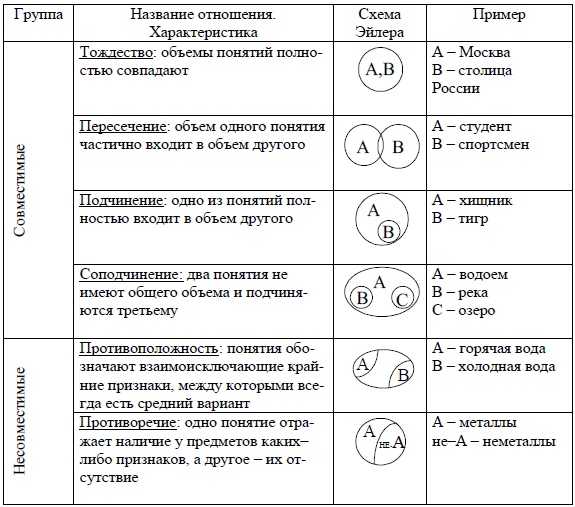 Такими понятиями будут: «сюзерен»
Такими понятиями будут: «сюзерен»
– «вассал» или «брат» – «сестра».
Классификация
понятий неразрывно связана с их логической
характеристикой. Определяя вид конкретного
понятия, мы тем самым делаем вывод
относительно него, характеризуем с
точки зрения логики как науки. Логическая
характеристика помогает определить
содержание и объем понятий и позволяет
в процессе рассуждения допускать как
можно меньше ошибок и с максимальной
эффективностью использовать то или
иное понятие в процессе доказательства.
№7
соотношение понятий. Сравнимые и не
сравнимые понятия . совместимые и
несовместимые понятия . Виды совместимых
и несовместимых понятий
| Собственно вот все задания, с чем то справилась, с чем то нет. 1. Дайте полную логическую характеристику следующим предметам: 2. б) Посягательство на честь и достоинство личности (1), клевета (2), оскорбление (3) 3. Проведите операцию деления данных понятий по избранным Вами признакам двумя способами: дихотомическим и по видообразующему признаку, укажите основание деления: пока не справилась 4. Проверьте правильность определения понятий, в неправильных случаях укажите, какие правила нарушаются и дайте правильное определение. Логика – это не политология. Личность – это совокупность социальных качеств человека, проявляющихся в его поведении. 6. Проведите операции обобщения следующих понятий: 7. Определите вид простого суждения, укажите субъект и предикат суждения, запишите его формулу, изобразите отношения между терминами с помощью кругов Эйлера. а) Некоторые рыбы не мечут икры. б) Все студенты выполнили задание. в) Ни один атом неделим. 8. Установите вид сложного суждения, укажите его составные части (простые суждения), запишите схему суждения с помощью символов, использую логические связки. 9. Сделайте выводы из следующих суждений по логическому квадрату, обоснуйте их. Все знающие логику знают правила силлогизма. 10. Сделайте вывод из данных суждений путем обращения, превращения, противопоставления предикату. 2. Превращение 11. Сделайте вывод из данных посылок, указав большую и меньшую посылку простого категорического силлогизма. Проверьте правильность вывода с помощью общих правил фигур силлогизма и круговых схем. Все углероды – простые тела Все киты — млекопитающие 12. Все львы — хищники, следовательно морские львы — тоже хищники. Не будучи математиком, вы не решите этой задачи. «И, может быть, я завтра умру!.. Одни скажут: он был добрый малый, другие – мерзавец. И то и другое будет ложно!» |
Эффективное переключение логического состояния в React
18 августа 2022 г.
Введение
Если мы хотим сохранить некоторое состояние в приложении React, мы используем хук useState . Это не плохо, но есть ли другие варианты? Давайте исследовать!
Создадим кастомный хук, который будет возвращать два значения — состояние и функцию для обновления состояния.
index.tsx
1import {useState} из «реагировать»
2
3type UseToggleReturnType = {
4 isToggled: boolean
5 toggle: () => void
6}
7
9000 7 8export const useToggle = (): UseToggleReturnType => {9 // Нам не нужно экспортировать функцию setIsToggled, так как мы хотим упростить использование хука.
10 const [isToggled, setIsToggled] = useState(false)
11
12 // Вместо предоставления функции `setIsToggled` у нас есть специализированная функция для переключения текущего состояния для нас
13 const toggle = () => {
14 setIsToggled(!isToggled)
15 }
16
17 return { isToggled, toggle }
900 07 18}
Тесты
Как вы знаете, я большой поклонник тестирования, так что давайте проведем несколько тестов!
index.tsx
1import {act, renderHook} from '@testing-library/react'
2
3import {useToggle} from '.
9 0007 4/use-toggle'
5// утверждаем, что возвращаются состояние и функция для переключения состояния
6describe('useToggle - тип возврата', () => {
7 const { result } = renderHook(() => {
8 return useToggle()
9 })
10
11 it('должен вернуть объект со свойством `isToggled`, которое равно false', () => {
12 expect(result.current).toHaveProperty ('isToggled')
13 expect(result.current.isToggled).toBe(false)
14 })
15
16 it('должен вернуть объект со свойством `toggle`, которое является функцией', () => {
17 expect(result.current).toHaveProperty('toggle ')
18 expect(result.current.toggle).toBeInstanceOf(Function)
19 })
20})
21
22// проверить, обновляется ли состояние при вызове функции переключения
23describe('useToggle - переключение', () => {
24 it('следует запустить функцию `toggle` и проверить, установлено ли для `isToggled` значение `true`', () => {
25 const { результат } = renderHook(() => {
26 return useToggle()
27 })
28
29 expect(result.
current.isToggled).toBe(false) 9001 0
30
31 act(() => {
32 result.current.toggle()
33 })
34
35 expect(result.current.isToggled).toBe(true)
36 })
37})
реализация useReducer
Поскольку у нас уже есть тесты, мы можем использовать хук useReducer для реализации той же функциональности.
Почему useReducer ? Потому что это более мощная версия useState , которая позволяет нам использовать функцию редуктора для обновления состояния на основе предыдущего состояния.
index.tsx
1импорт {useReducer} из «реакции»
2
3type UseToggleReturnType = {
4 isToggled: boolean 9001 0
5 переключение: () => пустота
6}
7
8export const useToggle = (): UseToggleReturnType => {
9 // При вызове функции toggle обратный вызов, переданный в useReducer, будет вызываться с предыдущим состоянием, возвращая противоположное состояние.

10 const [isToggled, toggle] = useReducer((previousValue) => {
11 return !previousValue
12 // `false` — начальное состояние
13 }, false)
14
15 возврат { isToggled, переключение }
16}
Тесты все еще проходят, и теперь мы можем использовать хук useReducer , чтобы реализовать то же самое, но с более надежным подходом.
Заключение
Целью этой статьи было не показать более короткий код или создать некоторую библиотеку, а показать, как использовать хук useReducer вместо хука useState для управления состоянием, которое должно быть переключаемым.
Вы нашли ошибки или у вас есть вопросы? Не стесняйтесь обращаться к Twitter.
Если вы не хотите пропустить следующую статью, нажмите на кнопку подписаться!
Поделиться этой публикацией в Твиттере
5.1: Булевы модели — таблицы истинности и диаграммы переходов состояний
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 22566
- Peter Woolf et al.

- Мичиганский университет
Введение в логические модели
Булева переменная — это переменная, которая может принимать только два значения: True или False. В большинстве приложений удобно представлять True числом 1, а False числом 0. Булева модель или булева сеть представляет собой набор логических переменных, которые связаны логическими правилами переключения, или Логические функции , соответствующие формату If-Then. Этот тип булевой модели известен как автономная модель и будет основным типом модели, обсуждаемой в этой статье.
В химическом машиностроении булевы модели могут использоваться для моделирования простых систем управления. Булевы функции можно использовать для моделирования переключателей насосов и клапанов, которые реагируют на показания датчиков, помогая поддерживать бесперебойную и безопасную работу системы. Простое приложение для контроля уровня CSTR включено в разработанный пример 1. В этом примере булева функция используется для закрытия потока на входе и открытия потока на выходе, когда уровень выше заданной точки.
Булевы функции
Булевы функции — это логические операторы, которые связывают две или более булевы переменные в системе и возвращают значение true или false. Логическое выражение — это группа логических функций, которые будут описаны ниже по отдельности. При вычислении значения логического выражения скобки используются для указания приоритета (работая изнутри наружу, как в алгебре). После этого ЛОГИЧЕСКАЯ ИНВЕРСИЯ всегда будет первой, а ЛОГИЧЕСКАЯ ЭКВИВАЛЕНТНОСТЬ последней, но порядок выполнения функций И, ИЛИ и ИСКЛЮЧАЮЩЕЕ ИЛИ указывается в скобках.
Описание и примеры этих функций приведены ниже. Краткое описание каждой из функций можно найти после примеров.
ЛОГИЧЕСКАЯ ИНВЕРСИЯ
ЛОГИЧЕСКАЯ ИНВЕРСИЯ — это функция, которая возвращает противоположное значение переменной. Функция обозначается как простое число переменной (например, A’ или B’). Например, если мы говорим, что A истинно (A=1), то функция A’ вернет false (A’=0). Аналогично, если мы скажем, что A ложно (A=0), то функция A’ вернет true (A’=1).
Пример:
A=1, B=A’, затем B=0
AND
Функция AND связывает две или более булевы переменные и возвращает истину тогда и только тогда, когда обе переменные истинны. Точка используется для обозначения функции И или просто опускается. Например, «A и B» можно записать как «A•B» или как «AB». В этом примере функция AND вернет истинное значение только в том случае, если обе логические переменные A и B имеют значение 1.
Примеры:
| Переменные | Результаты |
|---|---|
| А=1, В=1 | АВ = 1 |
| А=1, В=0 | АВ = 0 |
| А=1, В=1, С=1 | АВС = 1 |
| А=1, В=0, С=1 | АВС = 0 |
ИЛИ
Функция ИЛИ связывает две или более логических переменных и возвращает значение true, если какие-либо переменные, на которые ссылаются, имеют значение true. Плюс используется для обозначения функции ИЛИ. Например, «A или B» можно записать как «A+B». В этом примере функция ИЛИ вернет значение true, если любая логическая переменная, A или B, имеет значение 1.
Плюс используется для обозначения функции ИЛИ. Например, «A или B» можно записать как «A+B». В этом примере функция ИЛИ вернет значение true, если любая логическая переменная, A или B, имеет значение 1.
Примеры:
| Переменные | Результаты |
|---|---|
| А=1, В=1 | А+В = 1 |
| А=1, В=0 | А+В = 1 |
| А=0, В=0 | А+В = 0 |
| А=0, В=0, С=1 | А+В+С = 1 |
| А=0, В=0, С=0 | А+В+С = 0 |
ИСКЛЮЧАЮЩЕЕ ИЛИ
Функция ИСКЛЮЧАЮЩЕЕ ИЛИ связывает две или более логические переменные и возвращает true только тогда, когда одна из переменных верна и все другие переменные ложны. Он возвращает ложь , когда более одной переменных истинны, или все переменные ложны. Очерченный плюс используется для обозначения функции ИСКЛЮЧАЮЩЕЕ ИЛИ. Например, «A EXCLUSIVE OR B» можно записать как «AB».
Он возвращает ложь , когда более одной переменных истинны, или все переменные ложны. Очерченный плюс используется для обозначения функции ИСКЛЮЧАЮЩЕЕ ИЛИ. Например, «A EXCLUSIVE OR B» можно записать как «AB».
Примеры:
| Переменные | Результаты |
|---|---|
| А=1, В=1 | АВ = 0 |
| А=1, В=0 | АВ = 1 |
| А=0, В=1 | АВ = 1 |
| А=0, В=0 | АВ = 0 |
| А=0, В=0, С=0 | АВС = 0 |
| А=1, В=0, С=0 | АВС = 1 |
| А=1, В=0, С=1 | АВС = 0 |
| А=1, В=1, С=1 | АВС = 0 |
ЛОГИЧЕСКАЯ ЭКВИВАЛЕНТНОСТЬ
Функция ЛОГИЧЕСКАЯ ЭКВИВАЛЕНТНОСТЬ приравнивает две логические переменные или выражения. Функция ЛОГИЧЕСКАЯ ЭКВИВАЛЕНТНОСТЬ, обозначенная как =, присваивает булевой переменной значение true или false в зависимости от значения переменной или выражения, с которым она приравнивается. Например, ЛОГИЧЕСКАЯ ЭКВИВАЛЕНТНОСТЬ B может быть записана как A = B. В этом примере значению A будет присвоено значение B.
Функция ЛОГИЧЕСКАЯ ЭКВИВАЛЕНТНОСТЬ, обозначенная как =, присваивает булевой переменной значение true или false в зависимости от значения переменной или выражения, с которым она приравнивается. Например, ЛОГИЧЕСКАЯ ЭКВИВАЛЕНТНОСТЬ B может быть записана как A = B. В этом примере значению A будет присвоено значение B.
Логические сети
Как сказано во введении, логическая сеть представляет собой систему логических уравнений. В химической инженерии булевы сети, вероятно, будут зависеть от внешних входных данных как средства управления физической системой. Однако следующие разделы относятся в основном к синхронным автономным системам. Автономная система — это система, полностью независимая от внешних воздействий. Каждая логическая переменная зависит от состояния других логических переменных в системе, и никакая переменная не управляется внешним вводом. Синхронная система — это система, в которой логическое переключение (изменение логических переменных) происходит одновременно для всех переменных на основе значений, предшествующих изменению.
Вот пример автономной булевой сети:
| Логические функции |
| А = В+С’ |
| Б = АС |
| С = А’ |
Таблицы истинности
Таблица истинности представляет собой таблицу всех возможных состояний булевой модели в различных временных рамках. Простая таблица истинности показывает потенциальные начальные состояния в момент времени T i и соответствующие последующие состояния во время T i+1 булевой сети. Таблицы истинности могут дать более четкое представление о том, как применяются правила и как они влияют на каждую ситуацию. Следовательно, они помогают гарантировать, что каждый выход имеет только один управляющий оператор, чтобы логические правила не конфликтовали друг с другом.
Составление таблиц истинности
- Составьте таблицу с соответствующим количеством столбцов для каждой переменной; по одному на каждый вход и выход.

- Левая часть столбца должна содержать все возможные перестановки входных переменных в момент времени T i . Одним из способов добиться этого может быть перечисление всех возможных комбинаций в возрастающем двоичном порядке.
- Правая часть столбца должна содержать соответствующий результат выходных переменных в последующий момент времени T i+1 . Общий пример этого с 2 переменными можно увидеть ниже:
Быстрый способ проверить, есть ли у вас все возможные перестановки, состоит в том, что их должно быть 2 x возможных перестановок для входных переменных X.
Пример таблицы истинности
Система образцов, которую мы будем использовать, основана на технологии водородных топливных элементов. Уравнение работы водородных топливных элементов:
\[\ce{h3 + O2 -> h3O}. \номер\]
Одним из аспектов топливных элементов с протонообменной мембраной (PEM) (тип топливного элемента) является то, что производительность топливного элемента сильно зависит от относительной влажности системы (если влажность становится слишком высокой , топливный элемент затопится и H 2 и O 2 не смогут дозвониться до ячейки. Если влажность упадет слишком низко, топливный элемент высохнет, и производительность упадет.) Задача состоит в том, чтобы создать булевую модель для этой упрощенной системы управления водными ресурсами.
Если влажность упадет слишком низко, топливный элемент высохнет, и производительность упадет.) Задача состоит в том, чтобы создать булевую модель для этой упрощенной системы управления водными ресурсами.
Система производит пар внутри системы, и имеется вентиляционное отверстие для выпуска пара, если система становится слишком насыщенной. В нашей системе мы будем предполагать, что входы стехиометричны и полностью реагируют. Также будем считать, что повышение давления от пара незначительно по сравнению с изменением относительной влажности. Единственная рассматриваемая переменная – это % относительной влажности в системе.
- примечание: это не то, как на самом деле работает управление водой в системе топливных элементов, но это простой пример.
A представляет ответ контроллера влажности (0 указывает на относительную влажность или %RH < 80%, 1 указывает на %RH >80%)
B представляет состояние клапана (0 закрыт, 1 открыт)
Соответствующее логическое значение функции для этой модели приведены ниже (обычно вам придется разработать их самостоятельно, чтобы они соответствовали желаемым критериям):
A = A
B = A
Для этого примера с 2 входными переменными имеется 2 2 = 4 возможных перестановки и 2 2 = 4 строки. Результирующие перестановки для выходов: Для A, где Y=1, число нулей и единиц равно 2 (Y-1) =2 (1-1) =1. Для B, где Y=2, число нулей и единиц равно 2 (Y-1) =2 (2-1) =2.
Результирующие перестановки для выходов: Для A, где Y=1, число нулей и единиц равно 2 (Y-1) =2 (1-1) =1. Для B, где Y=2, число нулей и единиц равно 2 (Y-1) =2 (2-1) =2.
Результирующая таблица истинности представлена ниже:
Диаграммы переходов состояний
Диаграмма переходов состояний представляет собой графический способ просмотра таблиц истинности. Это достигается путем рассмотрения каждого отдельного начального состояния и его результирующего состояния. Переход из одного состояния в другое изображается стрелкой. Затем они собираются вместе, как мозаика, пока не встанут на место. Когда одно состояние ведет к самому себе, оно просто указывает на себя. Следующий пример основан на таблице истинности из предыдущего раздела.
В этом примере есть два цикла состояния. Цикл состояний — это комбинация состояний, в которые система постоянно входит и входит снова. Для конечного числа состояний всегда будет существовать хотя бы один цикл состояний.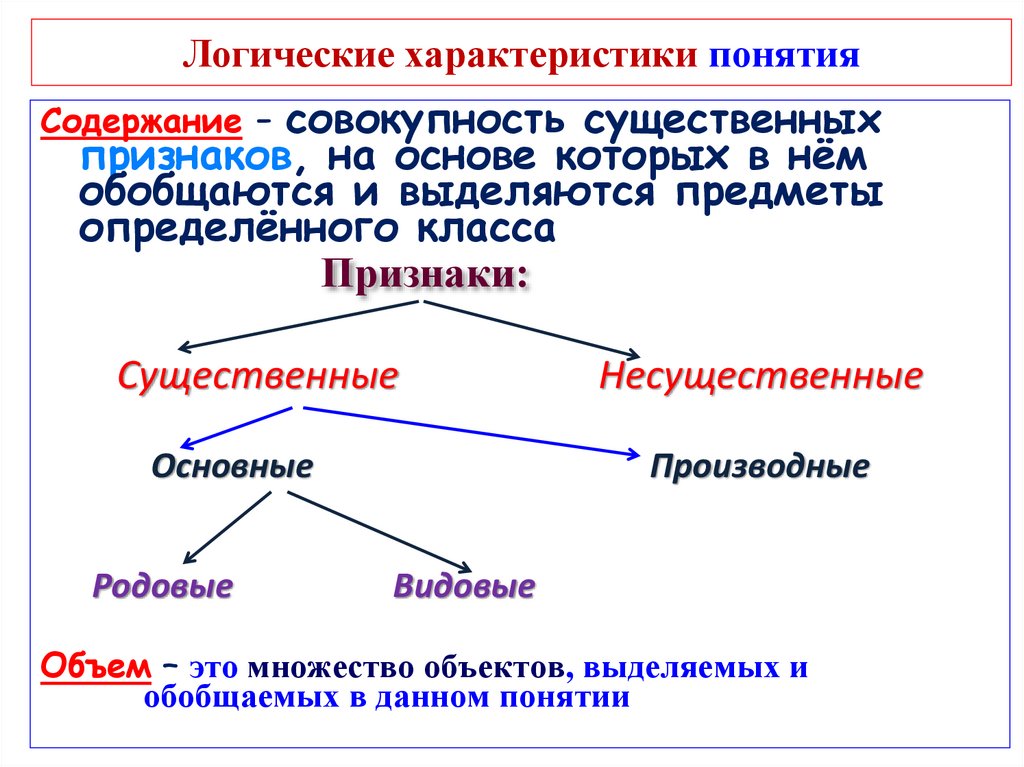 Цикл состояний также представляет собой путь или блок-схему, показывающую «процесс принятия решений» в булевой сети. Эта особенность является прямым следствием двух атрибутов булевых сетей:
Цикл состояний также представляет собой путь или блок-схему, показывающую «процесс принятия решений» в булевой сети. Эта особенность является прямым следствием двух атрибутов булевых сетей:
- Конечное число состояний
- Детерминированный (существует определенный набор правил, определяющий следующее состояние, в которое будет введен)
В примере, представленном в предыдущем разделе, было два цикла состояний. Одним из преимуществ циклов состояний является то, что они легко позволяют вам увидеть, где ваша модель в конечном итоге зациклится, и есть ли какие-либо состояния, которые не учитываются должным образом вашей моделью. На предыдущей диаграмме, если контроллер влажности указывал, что влажность ниже установленного значения, он закрывал клапан или удерживал его закрытым. Если контроллер влажности показывал, что влажность выше установленного значения, он либо открывал клапан, либо удерживал его открытым.
Рассмотрим эту альтернативную систему.
В этом примере состояние цикла говорит, что если счетчик сообщает, что влажность ниже заданного значения, он будет циклически открывать и закрывать вентиляционный клапан. Это повредит системе и не является желаемым результатом модели.
Что касается вопросов безопасности и функциональности, инженер по управлению технологическим процессом должен рассмотреть все возможности при проектировании любой булевой сети, моделирующей реальную систему.
Ограничения логических сетей
Преимущества булевых сетей
- В отличие от обыкновенных дифференциальных уравнений и большинства других моделей, булевы сети не требуют ввода параметров.
- быстро и легко вычисляются с помощью компьютеров.
- можно использовать для моделирования широкого спектра действий и событий.
- Булевы сети могут использоваться для аппроксимации обыкновенных дифференциальных уравнений при наличии бесконечного числа состояний.

Булевы модели
Булевы сети
Недостатки булевых сетей
- Булевы сети ограничены выполнением очень простых математических операций. Их нельзя использовать для исчисления и расчета больших величин.
- имеют относительно низкое разрешение по сравнению с другими моделями.
- Создание логических сетей вручную требует очень много времени и сложностей.
Булевы модели
Пример \(\PageIndex{1}\)
Гипотетический CSTR должен поддерживать уровень жидкости ниже отметки безопасности с помощью датчика L1 на соответствующей отметке и регулирующего клапана, размещенного на входе и выходе потоки – V1 и V2 соответственно. Типичное применение вышеупомянутой системы может включать гетерогенно катализируемую жидкую реакцию (реакции) с жидким продуктом (продуктами).
Раствор
Условные обозначения
Датчик уровня воды
| L1 | 0 | 1 |
| уровень воды | желательно | слишком высокий |
Клапан
| В | 0 | 1 |
| позиция | закрытый | открыть |
Исходное состояние
Предположим, что CSTR пуст и заполняется. CSTR, будучи пустым, устанавливает значение L1 равным нулю. Заполнить CSTR можно, открыв клапан 1 — V1, приняв значение единицы, и закрыв клапан 2 — V2, приняв значение нуля.
CSTR, будучи пустым, устанавливает значение L1 равным нулю. Заполнить CSTR можно, открыв клапан 1 — V1, приняв значение единицы, и закрыв клапан 2 — V2, приняв значение нуля.
В координатной форме начальное состояние таково: (L1, V1, V2) = (0, 1, 0)
Интерпретация проблемы
Пусть h — уровень воды, а WL1 — отметка безопасности, определенная в CSTR. Система может принять одно из следующих состояний в любой момент времени:
1) h < WL1 : желаемый уровень воды
Максимальное производство химиката побуждает систему оставаться в своем текущем состоянии, то есть в исходном состоянии. (L1, V1, V2)final = (0, 1, 0) конечное состояние
2) h > WL1 : слишком высокий уровень воды
Для предотвращения затопления необходимо опорожнить бак. Таким образом, клапан 1 (V1) должен быть закрыт, чтобы остановить подачу, а клапан 2 (V2) должен быть открыт, чтобы слить лишнюю воду выше безопасной водяной отметки. (L1, V1, V2)’ = (1, 1, 0) срабатывание клапана (L1, V1, V2)final = (1, 0, 1) конечное состояние
Цикл состояний
Физическое значение 9001 0
Ссылки
- Джеймс Э.
 Палмер и Дэвид Э. Перлман (1993). Очерк теории и проблем введения в цифровые системы Шаума , McGraw-Hill Professional. ISBN 0070484392
Палмер и Дэвид Э. Перлман (1993). Очерк теории и проблем введения в цифровые системы Шаума , McGraw-Hill Professional. ISBN 0070484392 - Стюарт А. Кауфман (1993). Истоки самоорганизации порядка и отбора в эволюции , издательство Оксфордского университета. ISBN 0195079515
Авторы и ссылки
- Джозеф Каслер, Андри Харьянто, Сет Кале и Вейин Сюй, Адхи Паисепутра, Эндрю Ким, Хиллари Каст, Стефани Клето
Эта страница под названием 5.1: Булевы модели — таблицы истинности и диаграммы переходов состояний распространяется под лицензией CC BY 3.0, автором, ремиксом и/или куратором этой страницы являются Peter Woolf et al. через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Питер Вульф и др.

 Определите вид отношений между понятиями, изобразите их с помощью круговых систем (кругов Эйлера):
Определите вид отношений между понятиями, изобразите их с помощью круговых систем (кругов Эйлера):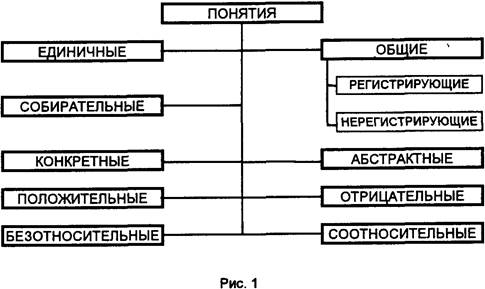 Проведите операции ограничения следующих понятий:
Проведите операции ограничения следующих понятий: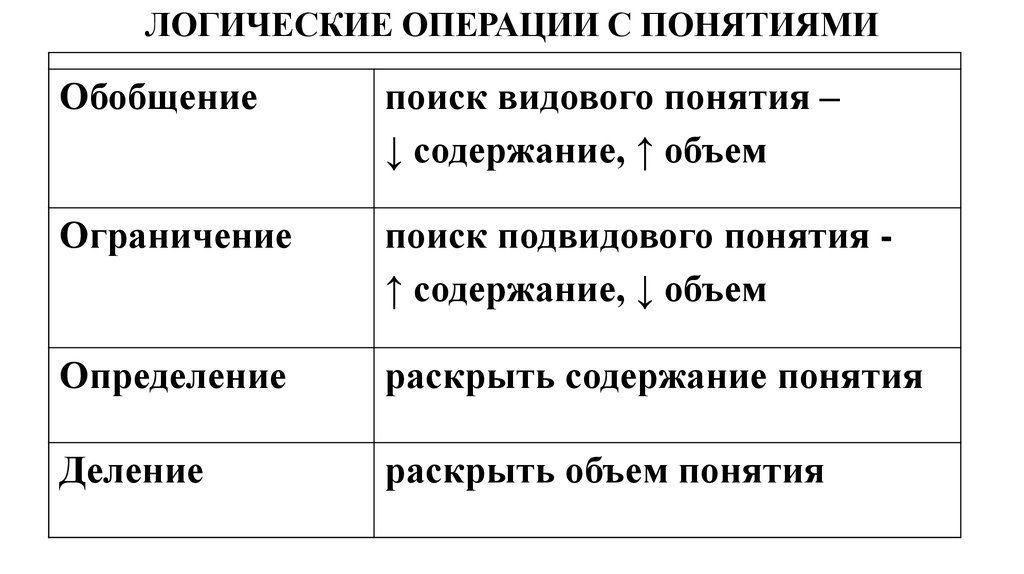 C
C Восстановите энтимему, проверьте правильность полученного умозаключения:
Восстановите энтимему, проверьте правильность полученного умозаключения: /use-toggle'
/use-toggle'  current.isToggled).toBe(false) 9001 0
current.isToggled).toBe(false) 9001 0 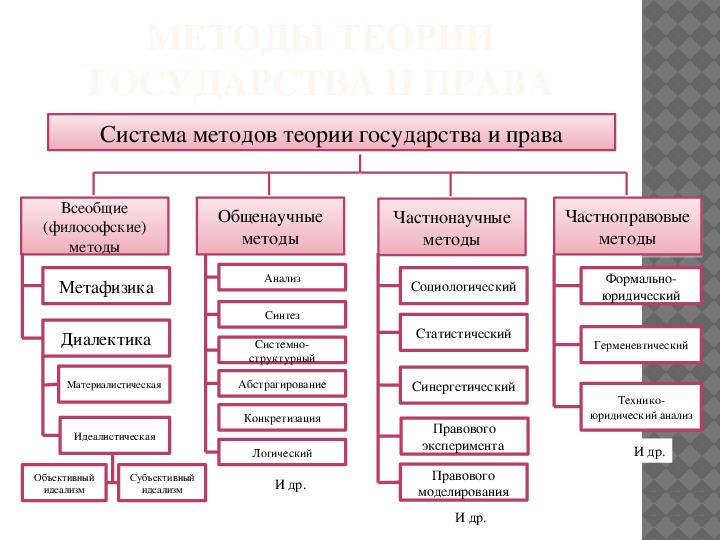


 Палмер и Дэвид Э. Перлман (1993). Очерк теории и проблем введения в цифровые системы Шаума , McGraw-Hill Professional. ISBN 0070484392
Палмер и Дэвид Э. Перлман (1993). Очерк теории и проблем введения в цифровые системы Шаума , McGraw-Hill Professional. ISBN 0070484392