Содержание
Как получить среднеквадратичное значение формы импульса и прямоугольного сигнала – Mastering Electronics Design
Адриан С. Настасе
Среднеквадратичное значение формы импульсного сигнала можно легко рассчитать, начиная с определения среднеквадратичного значения. Форма импульсного сигнала показана на рисунке 1. Отношение t1/T представляет собой коэффициент заполнения импульсного сигнала. Как показано в других статьях на этом веб-сайте (MasteringElectronicsDesign.com: Как получить среднеквадратичное значение трапециевидной формы волны и MasteringElectronicsDesign.com: Как получить среднеквадратичное значение треугольной формы волны), определение среднеквадратичного значения представляет собой интеграл за период сигнала. как в уравнении (1).
Рисунок 1
| (1) |
Импульсная функция с переменной «время» является константой, которая представляет собой амплитуду сигнала между 0 и t1 и нулем от t1 до T, как в (2).
| (2) |
, где с u1(t) я отметил функцию формы волны на рисунке 1. После замены u1(t) в уравнении (1) мы можем найти среднеквадратичное значение в квадрате, как в следующем выражении.
| (3) |
Следовательно, среднеквадратичное значение импульсного сигнала равно
| (4) |
Это выражение также можно найти в (5)
| (5) |
где с D я отметил коэффициент заполнения импульсного сигнала, D = t1/T.
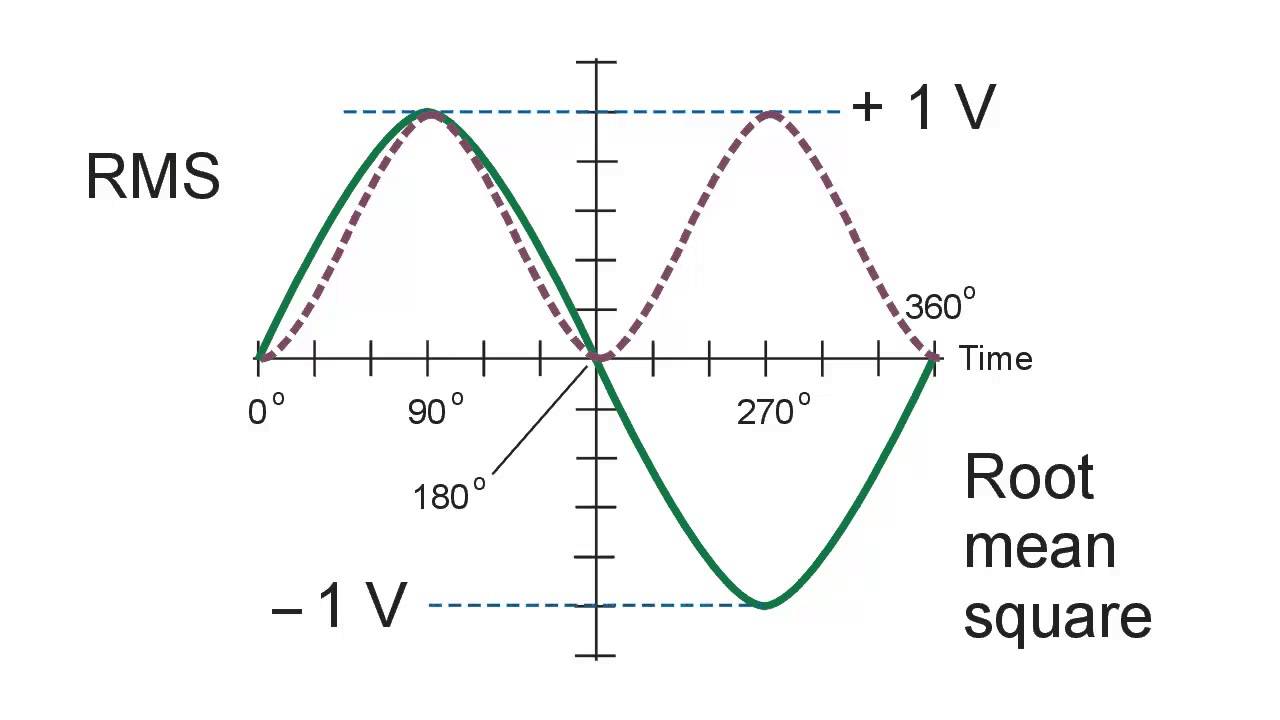
Что делать, если импульсный сигнал биполярный, как на рис. 2? 9Рис. 2 Чтобы вычислить среднеквадратичное значение, давайте разделим сигнал на две части: от 0 до t1 и от t1 до T, как в (6).
| (6) |
где с u11(t) и u12(t) я отметил две части формы волны на рисунке 2.
Среднеквадратичное значение u11(t) идентично показанному в уравнении (3).
| (7) |
Аналогичным образом можно рассчитать среднеквадратичное значение u12(t):
| (8) |
Затем вычисляется общее среднеквадратичное значение биполярной импульсной волны путем применения квадратного корня из суммы квадратов u11 RMS и u12 RMS .
| (9) |
После расчетов среднеквадратичное значение биполярного импульсного сигнала равно
| (10) |
Как видите, среднеквадратичное значение биполярного импульса не зависит от его скважности и равно его амплитуде.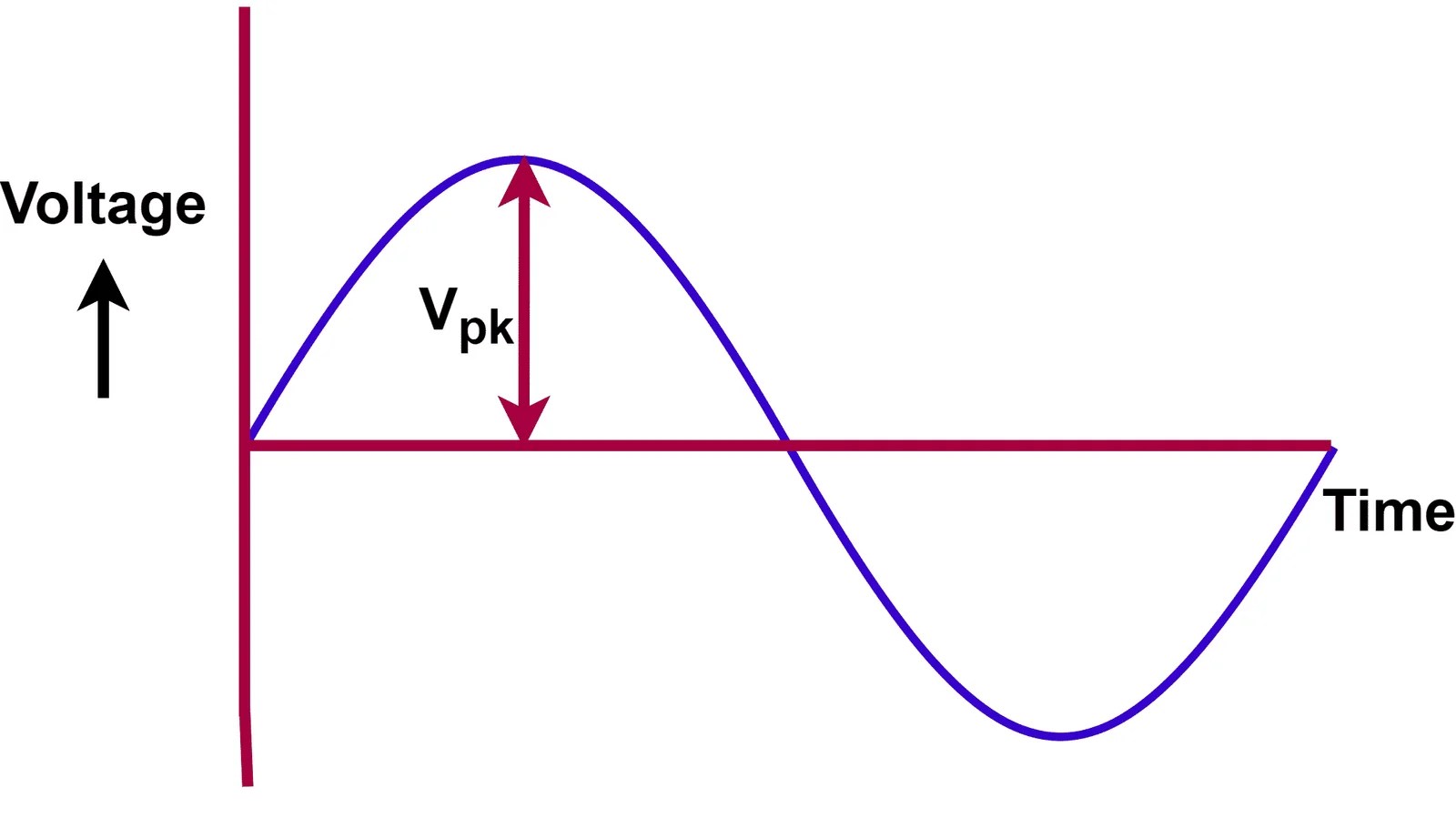
Зная среднеквадратичное значение импульсного сигнала, мы можем легко вычислить среднеквадратичное значение периодического прямоугольного сигнала. Прямоугольная волна на рисунке 3 представляет собой импульсный сигнал с коэффициентом заполнения 50%. Его среднеквадратичное значение можно рассчитать из уравнения (5), где D = 1/2. Его среднеквадратичное значение приведено в (11).
Рисунок 3
| (11) |
>>> <<<
Мы используем файлы cookie и другие технологии отслеживания, чтобы улучшить ваш просмотр на нашем сайте, показывать персонализированный контент и таргетированную рекламу, анализировать трафик сайта и понимать, откуда приходит наша аудитория. Чтобы узнать больше, нажмите ссылку Узнать больше. Кроме того, ознакомьтесь с нашей Политикой конфиденциальности, которая также была обновлена и вступила в силу 24 мая 2018 г. Выбрав «Принимаю», вы соглашаетесь на использование нами файлов cookie и других технологий отслеживания. Узнать больше.
Выбрав «Принимаю», вы соглашаетесь на использование нами файлов cookie и других технологий отслеживания. Узнать больше.
Руководство по сценариям SIMetrix: функция среднеквадратичного значения
Возвращает кумулятивное среднеквадратичное значение аргумента
Аргументы
| Число | Тип | Принудительный | По умолчанию | Описание |
| 1 | реальный массив | Да | Вектор |
Возвращает
Тип возвращаемого значения: реальный массив
Возвращает вектор совокупного среднеквадратичного значения входа.