Содержание
Угловая скорость. Формула угловой скорости :: SYL.ru
Расстояние и время, которое уходит на преодоление этого расстояния, связывает физическое понятие – скорость. И у человека, как правило, не вызывает вопросов определение этой величины. Все понимают, что двигаться на автомобиле со скоростью 100 км/ч — значит за один час проехать 100 километров.
А как быть, если тело вращается? Например, обычный бытовой вентилятор делает с десяток оборотов в секунду. И в то же время скорость вращения лопастей такова, что их запросто можно остановить рукой без вреда для себя. Земля вокруг своей звезды – Солнца — делает один оборот за целый год, а это более 30 миллионов секунд, но скорость её движения по околозвёздной орбите составляет около 30 километров за одну секунду!
Как же связать привычную скорость с быстротой вращения, как выглядит формула угловой скорости?
Понятие угловой скорости
Понятие угловой скорости используется в изучении законов вращения. Оно применяется ко всем вращающимся телам. Будь то вращение некоторой массы вокруг другой, как в случае с Землёй и Солнцем, или же вращение самого тела вокруг полярной оси (суточное вращение нашей планеты).
Будь то вращение некоторой массы вокруг другой, как в случае с Землёй и Солнцем, или же вращение самого тела вокруг полярной оси (суточное вращение нашей планеты).
Отличие угловой скорости от линейной в том, что она фиксирует изменение угла, а не расстояния в единицу времени. В физике угловую скорость принято обозначать буквой греческого алфавита «омега» — ω.
Классическая формула угловой скорости вращения рассматривается так.
Представим, что вокруг некоторого центра А вращается физическое тело с постоянной скоростью. Его положение в пространстве относительно центра определяется углом φ. В некоторый момент времени t1 рассматриваемое тело находится в точке В. Угол отклонения тела от начального φ1.
Затем тело перемещается в точку С. Оно находится там в момент времени t2. Время, понадобившееся для данного перемещения:
∆t = t2 – t1.
Меняется и положение тела в пространстве. Теперь угол отклонения равен φ2. Изменение угла за период времени ∆t составило:
∆φ = φ2 – φ1.
Теперь формула угловой скорости формулируется следующим образом: угловая скорость определяется как отношение изменения угла ∆φ за время ∆t.
Единицы измерения угловой скорости
Скорость движения тела линейная измеряется в разных величинах. Движение автотранспорта по дорогам привычно указывают в километрах в час, морские суда делают узлы – морские мили в час. Если же рассматривать движение космических тел, то тут чаще всего фигурируют километры в секунду.
Угловая скорость в зависимости от величины и от предмета, который вращается, также измеряется в разных единицах.
Радианы в секунду (рад/с) – классическое мерило скорости в международной системе единиц (СИ). Показывают – на сколько радиан (в одном полном обороте 2 ∙ 3,14 радиан) успевает повернуться тело за одну секунду.
Обороты в минуту (об/мин) – самая распространённая единица для обозначения скоростей вращения в технике. Валы двигателей как электрических, так и автомобильных выдают именно (достаточно посмотреть на тахометр в своём автомобиле) обороты в минуту.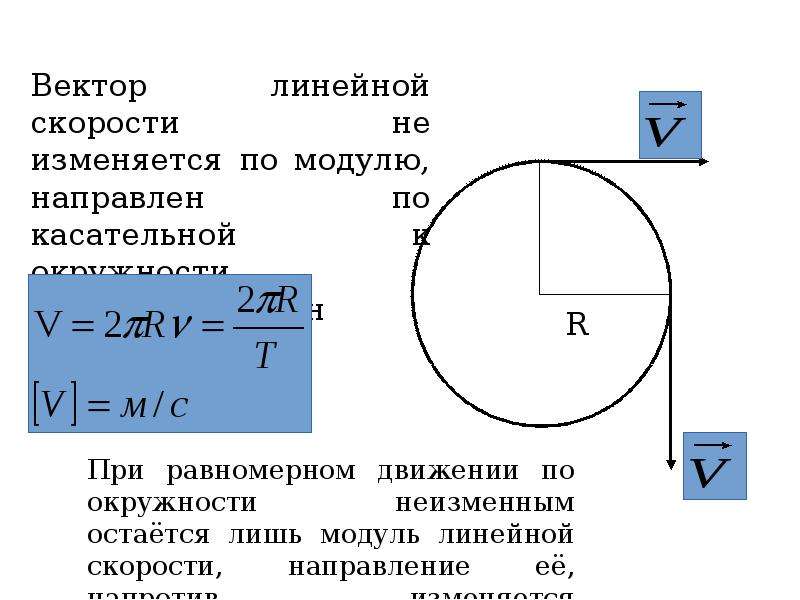
Обороты в секунду (об/с) – используется реже, прежде всего в образовательных целях.
Период обращения
Иногда для определения скорости вращения удобнее пользоваться другим понятием. Периодом обращения принято называть время, за которое некое тело делает оборот 360° (полный круг) вокруг центра вращения. Формула угловой скорости, выраженная через период обращения, принимает вид:
ω = 2П / Т.
Выражать периодом обращения быстроту вращения тел оправдано в случаях, когда тело вращается относительно медленно. Вернёмся к рассмотрению движения нашей планеты вокруг светила.
Формула угловой скорости позволяет вычислить её, зная период обращения:
ω = 2П/31536000 = 0,000000199238499086111 рад/с.
Глядя на полученный результат, можно понять, почему, рассматривая вращение небесных тел, удобнее пользоваться именно периодом обращения. Человек видит перед собой понятные цифры и наглядно представляет себе их масштаб.
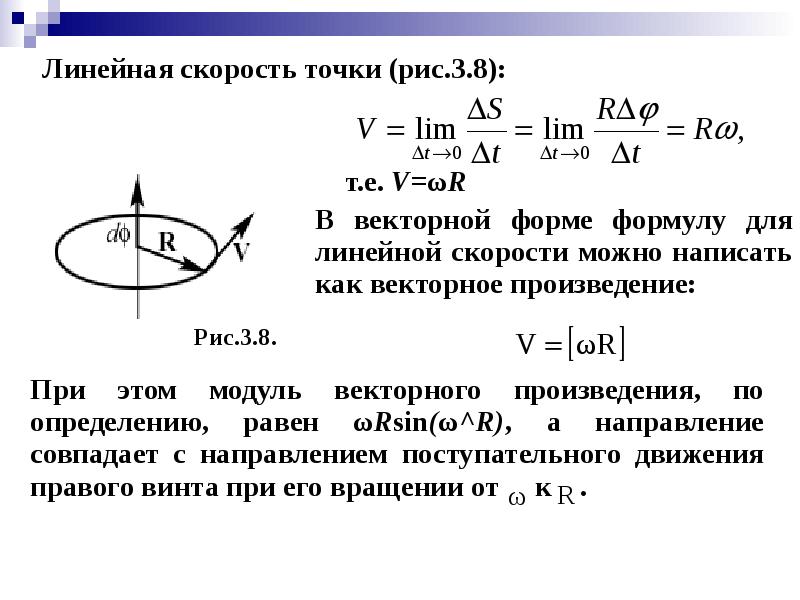
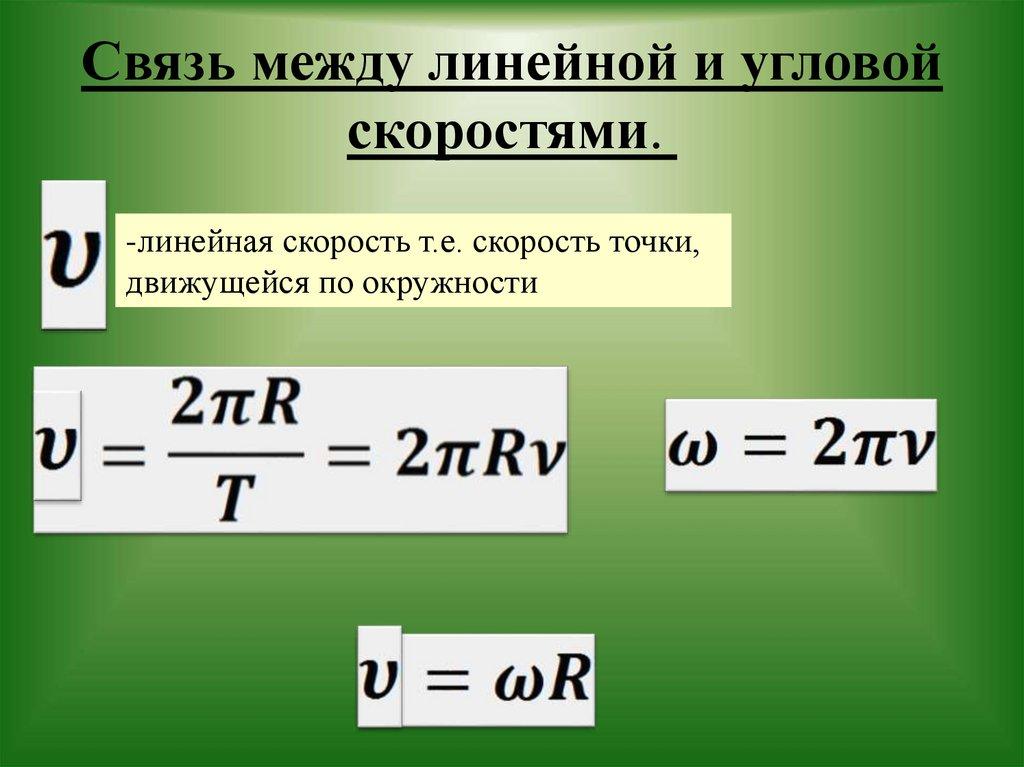
Связь угловой и линейной скоростей
В некоторых задачах должны быть определены линейная и угловая скорость. Формула трансформации проста: линейная скорость тела равняется произведению угловой скорости на радиус вращения. Как это показано на рисунке.
Формула трансформации проста: линейная скорость тела равняется произведению угловой скорости на радиус вращения. Как это показано на рисунке.
«Работает» выражение и в обратном порядке, с его помощью определяется и угловая скорость. Формула через скорость линейную получается путём несложных арифметических манипуляций.
Угловая скорость: формула частоты вращения
Иногда применительно к автомобилям всплывают вопросы из математики и физики. В частности, одним из таких вопросов является угловая скорость. Она имеет отношение как к работе механизмов, так и к прохождению поворотов. Разберёмся же, как определить эту величину, в чём она измеряется и какими формулами тут нужно пользоваться.
Содержание
- Как определить угловую скорость: что это за величина?
- Формула времени, за которое вращается точка по окружности заданного радиуса
- Угол поворота и период обращения
- Чему равна угловая скорость в конкретных случаях?
- Связь угловой и линейной скоростей
- Ускорение, момент и связь их с массой
- Шарнир как пример передачи импульса
Как определить угловую скорость: что это за величина?
С физико-математической точки зрения эту величину можно определить следующим образом: это данные, которые показывают, как быстро некая точка осуществляет оборот вокруг центра окружности, по которой она движется.
ПОСМОТРЕТЬ ВИДЕО
Эта, казалось бы, чисто теоретическая величина, имеет немалое практическое значение при эксплуатации автомобиля. Вот лишь несколько примеров:
- Необходимо правильно соотносить движения, с которыми вращаются колёса при повороте. Угловая скорость колеса автомобиля, движущегося по внутренней части траектории, должна быть меньше, чем у внешнего.
- Требуется рассчитывать, насколько быстро в автомобиле вращается коленвал.
- Наконец, сама машина, проходя поворот, тоже имеет определённую величину параметров движения – и от них на практике зависит устойчивость автомобиля на трассе и вероятность опрокидывания.
Формула времени, за которое вращается точка по окружности заданного радиуса
Для того, чтобы рассчитывать угловую скорость, используется следующая формула:
ω = ∆φ /∆t
Где:
- ω (читается «омега») – собственно вычисляемая величина.

- ∆φ (читается «дельта фи») – угол поворота, разница между угловым положением точки в первый и последний момент времени измерения.
- ∆t
(читается «дельта тэ») – время, за которое произошло это самое смещение. Точнее, поскольку «дельта», это означает разницу между значениями времени в момент, когда было начато измерение и когда закончено.
Приведённая выше формула угловой скорости применяется лишь в общих случаях. Там же, где речь идёт о равномерно вращающихся объектах или о связи между движением точки на поверхности детали, радиусом и временем поворота, требуется использовать другие соотношения и методы. В частности, тут уже будет необходима формула частоты вращения.
Угловая скорость измеряется в самых разных единицах. В теории часто используется рад/с (радиан в секунду) или градус в секунду. Однако эта величина мало что означает на практике и использоваться может разве что в конструкторской работе. На практике же её больше измеряют в оборотах за секунду (или минуту, если речь идёт о медленных процессах). В этом плане она близка к частоте вращения.
В этом плане она близка к частоте вращения.
Угол поворота и период обращения
Гораздо более часто, чем угол поворота, используется частота вращения, которая показывает, сколько оборотов делает объект за заданный период времени. Дело в том, что радиан, используемый для расчётов – это угол в окружности, когда длина дуги равна радиусу. Соответственно в целой окружности находится 2 π радианов. Число же π – иррациональное, и его нельзя свести ни к десятичной, ни к простой дроби. Поэтому в том случае, если происходит равномерное вращение, проще считать его в частоте. Она измеряется в об/мин – оборотах в минуту.
Если же дело касается не длительного промежутка времени, а лишь того, за который происходит один оборот, то здесь используется понятие периода обращения. Она показывает, как быстро совершается одно круговое движение. Единицей измерения здесь будет выступать секунда.
Связь угловой скорости и частоты вращения либо периода обращения показывает следующая формулы:
ω = 2 π / T = 2 π *f,
где:
- ω – угловая скорость в рад/с;
- T – период обращения;
- f – частота вращения.

Получить любую из этих трёх величин из другой можно с помощью правила пропорций, не забыв при этом перевести размерности в один формат (в минуты либо секунды)
Чему равна угловая скорость в конкретных случаях?
Приведём пример расчёта на основе приведённых выше формул. Допустим, имеется автомобиль. При движении на 100 км/ч его колесо, как показывает практика, делает в среднем 600 оборотов за минуту (f = 600 об/мин). Рассчитаем угловую скорость.
Для начала переведем об/мин в об/с. Для этого разделим 600 на 60 (число секунд в минуте) и получим 10 об/с . Попутно мы получили и период обращения: эта величина является обратной по отношению к частоте и при измерении в секундах 0,1 с.
Далее используем формулу:
ω = 2 π *f
Поскольку точно выразить π десятичными дробями невозможно, результат примерно равен будет 62,83 рад/с.
Связь угловой и линейной скоростей
На практике часто приходится проверять не только ту скорость, с какой изменяется угловое положение у вращающейся точки, но и скорость её самой применительно к линейному движению. В приведённом выше примере были сделаны расчёты для колеса – но колесо движется по дороге и либо вращается под действием скорости автомобиля, либо само ему эту скорость обеспечивает. Значит, каждая точка на поверхности колеса помимо угловой будет иметь и линейную скорость.
В приведённом выше примере были сделаны расчёты для колеса – но колесо движется по дороге и либо вращается под действием скорости автомобиля, либо само ему эту скорость обеспечивает. Значит, каждая точка на поверхности колеса помимо угловой будет иметь и линейную скорость.
Рассчитать её проще всего через радиус. Поскольку скорость зависит от времени (которым будет период обращения) и пройденного расстояния (которым является длина окружности), то, учитывая приведённые выше формулы, угловая и линейная скорость будут соотноситься так:
V = ωR
Где:
- V – линейная скорость;
- R – радиус.
Из формулы очевидно, что чем больше радиус, тем выше и значение такой скорости. Применительно к колесу с самой большой скоростью будет двигаться точка на внешней поверхности протектора (R максимален), но вот точно в центре ступицы линейная скорость будет равна нулю.
Ускорение, момент и связь их с массой
Помимо приведённых выше величин, с вращением связано ещё несколько моментов. Учитывая же, сколько в автомобиле крутящихся деталей разного веса, их практическое значение нельзя не учесть.
Учитывая же, сколько в автомобиле крутящихся деталей разного веса, их практическое значение нельзя не учесть.
Равномерное вращение – это важная вещь. Вот только нет ни одной детали, которая бы всё время крутилась равномерно. Число оборотов любого крутящегося узла, от коленвала до колеса, всегда в конечном итоге растёт, а затем падает. И та величина, которая показывает, насколько выросли обороты, называется угловым ускорением. Поскольку она производная от угловой скорости, измеряется она в радианах на секунду в квадрате (как линейное ускорение – в метрах на секунду в квадрате).
С движением и её изменением во времени связан и другой аспект – момент импульса. Если до этого момента мы могли рассматривать только чисто математические особенности движения, то здесь уже нужно учитывать то, что каждая деталь имеет массу, которая распределена вокруг оси. Он определяется соотношением начального положения точки с учётом направления движения – и импульса, то есть произведения массы на скорость.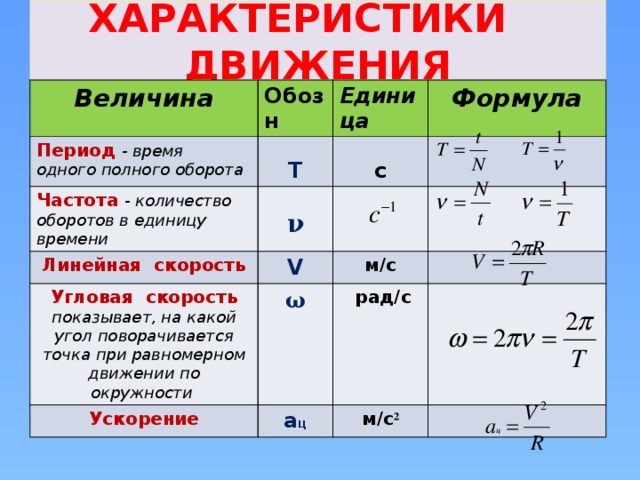 Зная момент импульса, возникающий при вращении, можно определить, какая нагрузка будет приходиться на каждую деталь при её взаимодействии с другой
Зная момент импульса, возникающий при вращении, можно определить, какая нагрузка будет приходиться на каждую деталь при её взаимодействии с другой
Шарнир как пример передачи импульса
Характерным примером того, как применяются все перечисленные выше данные, является шарнир равных угловых скоростей (ШРУС) . Эта деталь используется прежде всего на переднеприводных автомобилях, где важно не только обеспечить разный темп вращения колёс при повороте – но и при этом их управляемость и передачу на них импульса от работы двигателя.
ПОСМОТРЕТЬ ВИДЕО
Конструкция этого узла как раз и предназначена для того, чтобы:
- уравнивать между собой, как быстро вращаются колёса;
- обеспечивать вращение в момент поворота;
- гарантировать независимость задней подвеске.

В результате все формулы, приведённые выше, учитываются в работе ШРУС.
Линейная скорость — определение, формула, единицы измерения, примеры, приложения
Скорость — это скорость изменения положения объекта в определенном временном диапазоне. Когда объект движется по прямой траектории, его скорость называется линейной скоростью. Он определяется как отношение пройденного расстояния ко времени. Он обозначается буквой V и измеряется в системе СИ м/с. Это векторная величина.
Содержание
|
Что такое линейная скорость?
Линейная скорость — это мера «скорости изменения смещения по отношению ко времени, когда объект движется по прямолинейному пути». Это векторная величина . Формула линейной скорости [M] 0 [Л] 1 [Т] -1
Это векторная величина . Формула линейной скорости [M] 0 [Л] 1 [Т] -1
Линейная и угловая скорости связаны со скоростью объекта в зависимости от выбранной перспективы. Линейная скорость применяется к объекту, который движется, тогда как угловая скорость применяется к объектам, которые вращаются, таким как колесо, вращение Земли или волчок.
Формула линейной скорости
Линейная скорость зависит от расстояния, которое проходит объект за время. Линейное уравнение или формула линейной скорости определяется выражением
v = х/т
Где,
- v = Линейная скорость
- x = пройденное расстояние
- t = время, затраченное на преодоление расстояния (x).
Единицы линейной скорости
Линейная скорость измеряется в единицах СИ метр в секунду или м/с
Преобразование угловой скорости в линейную скорость
Все, что движется или вращается в круговом направлении, имеет как линейную скорость, так и угловую скорость.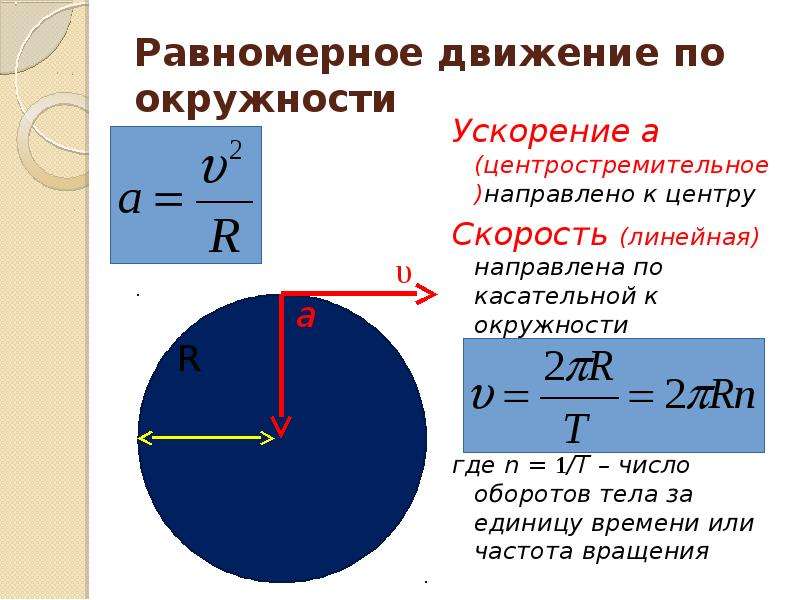 Угловая скорость – это отношение пройденного угла к количеству времени, необходимому для прохождения этого угла.
Угловая скорость – это отношение пройденного угла к количеству времени, необходимому для прохождения этого угла.
Угловая скорость выражает угловое смещение во времени и может быть выражена в радианах или градусах. Угловая скорость определяется с помощью вышеупомянутого уравнения.
Для расчета линейной скорости по угловой скорости можно применить формулу, где –
ω выражается в радианах/время,
r указывает радиус пройденного пути.
Подробнее: Угловое смещение
Постоянная линейная скорость
Когда тело движется с постоянной скоростью, не меняя своего направления, говорят, что оно движется с постоянной линейной скоростью. Линейная скорость указывает, что направление не изменилось, а постоянная показывает, что величина осталась постоянной.
Физика Похожие темы:
Часто задаваемые вопросы – Часто задаваемые вопросы
Q1
Что такое линейная скорость?
Линейная скорость определяется как векторная величина, обозначающая скорость изменения положения объекта от его положения равновесия по отношению к массе.
Q2
Как определить модуль линейной скорости точки B на звене AB относительно точки A?
Ниже приведено уравнение, которое используется для определения величины линейной скорости точки B на линии Ab относительно точки A:
ω*AB
Q3
Что такое тангенциальная составляющая?
Тангенциальная составляющая — это составляющая, при которой центростремительная составляющая параллельна скорости частицы.
Q4
Что такое радиальный компонент?
Радиальная составляющая — это составляющая, при которой центростремительная составляющая перпендикулярна скорости частицы.
Q5
Какова размерная формула углового момента?
[ML 2 T -1 ]
Q6
Что означает скорость смещения?
Скорость перемещения означает скорость тела, которая измеряется в метрах в секунду.
Q7
Что такое мгновенная скорость?
Мгновенная скорость – это скорость тела в данный момент. Единицей мгновенной скорости в СИ является мс -1 .
Единицей мгновенной скорости в СИ является мс -1 .
Q8
Как определить направление линейной скорости тела, движущегося по окружности?
По касательной определяется направление линейной скорости тела, движущегося по окружности.
Q9
Чему равен угол между линейной скоростью и угловой скоростью тела, движущегося по окружности?
Угол между линейной скоростью и угловой скоростью тела, движущегося по окружности, равен 90°.
Q10
Определение линейной скорости.
Скорость изменения смещения относительно времени, когда объект движется по прямому пути.
Q11
Напишите выражение для линейной скорости.
Выражение для линейной скорости:
v=xt
Q12
Запишите размерную формулу линейной скорости.
Размерная формула линейной скорости [ML 1 T -1 ]
Q13
Укажите верно или неверно.
 «Линейная скорость — это скалярная величина».
«Линейная скорость — это скалярная величина».
Ложь. Линейная скорость является векторной величиной.
Q14
Запишите тип движения, связанный с линейной скоростью.
Движение по прямой.
Q15
Запишите единицу линейной скорости в системе СИ.
SI Единица измерения линейной скорости – м/с.
Q16
Назовите виды скоростей, связанных с круговым движением.
Угловая скорость и линейная скорость.
Q17
Если объект проходит 3 метра за 2 секунды по прямой. Вычислите его линейную скорость.
Подставляя значения в v = x/t, мы получаем линейную скорость как 1,5 м/с.
Q18
Самолет летит на северо-восток. Если восточная составляющая его скорости равна 300 м/ч, с какой скоростью движется самолет?
424 м/ч.
Q19
Объект движется по круговой траектории. Как изменится его линейная скорость, если диаметр окружности уменьшить вдвое?
Посмотрите видео и узнайте больше о законах движения
Надеюсь, вы поняли линейную скорость, как она рассчитывается и ее формулу, а также термины и единицы измерения.
Следите за новостями BYJU’S, чтобы не пропустить еще таких интересных статей. Кроме того, зарегистрируйтесь в «BYJU’S — The Learning App», чтобы получить множество интерактивных, увлекательных видеороликов по физике и неограниченную академическую помощь.
6.1 Угол поворота и угловая скорость
Цели обученияУгол вращенияУгловая скоростьРешение задач, связанных с углом вращения и угловой скоростьюПрактические задачиПроверьте свое понимание
Цели обучения
К концу этого раздела вы сможете делать следующее: своему линейному аналогу
| угол поворота | угловая скорость | длина дуги |
| круговое движение | радиус кривизны | вращательное движение |
| спин | тангенциальная скорость |
Угол поворота
Что именно мы подразумеваем под круговым движением или вращением ? Вращательное движение – это круговое движение объекта вокруг оси вращения. Мы обсудим конкретно круговое движение и вращение. Круговое движение — это когда объект движется по круговой траектории. Примеры кругового движения включают гоночный автомобиль, мчащийся по круговой кривой, игрушку, прикрепленную к веревке, которая качается по кругу вокруг вашей головы, или круговое движение.0282 петля-петля на американских горках. Вращение — это вращение вокруг оси, проходящей через центр масс объекта, например, Земля, вращающаяся вокруг своей оси, колесо, вращающееся вокруг своей оси, вращение торнадо на пути разрушения или вращение фигуриста во время выступление на Олимпиаде. Иногда объекты будут вращаться во время кругового движения, например Земля, вращающаяся вокруг своей оси, вращаясь вокруг Солнца, но мы сосредоточимся на этих двух движениях отдельно.
Мы обсудим конкретно круговое движение и вращение. Круговое движение — это когда объект движется по круговой траектории. Примеры кругового движения включают гоночный автомобиль, мчащийся по круговой кривой, игрушку, прикрепленную к веревке, которая качается по кругу вокруг вашей головы, или круговое движение.0282 петля-петля на американских горках. Вращение — это вращение вокруг оси, проходящей через центр масс объекта, например, Земля, вращающаяся вокруг своей оси, колесо, вращающееся вокруг своей оси, вращение торнадо на пути разрушения или вращение фигуриста во время выступление на Олимпиаде. Иногда объекты будут вращаться во время кругового движения, например Земля, вращающаяся вокруг своей оси, вращаясь вокруг Солнца, но мы сосредоточимся на этих двух движениях отдельно.
При решении задач, связанных с вращательным движением, мы используем переменные, аналогичные линейным переменным (расстояние, скорость, ускорение и сила), но учитывающие кривизну или вращение движения. Здесь мы определяем угол поворота, который является угловым эквивалентом расстояния; и угловая скорость, которая является угловой эквивалентностью линейной скорости.
Здесь мы определяем угол поворота, который является угловым эквивалентом расстояния; и угловая скорость, которая является угловой эквивалентностью линейной скорости.
Когда объекты вращаются вокруг какой-либо оси — например, когда диск на рис. 6.2 вращается вокруг своего центра — каждая точка объекта движется по круговой траектории.
Рис. 6.2. Все точки на компакт-диске движутся по круговым траекториям. Ямки (точки) вдоль линии от центра к краю перемещаются на один и тот же угол ΔθΔθ за время ΔtΔt.
Длина дуги , , это расстояние, пройденное по круговой траектории. Радиус кривизны, r , является радиусом кругового пути. Оба показаны на рис. 6.3.
Рис. 6.3 Радиус ( r ) окружности повернут на угол ΔθΔθ. Длина дуги, ΔsΔs, представляет собой расстояние, пройденное по окружности.
Рассмотрим линию от центра компакт-диска до его края. В заданное время каждая яма (используемая для записи информации) на этой линии перемещается на один и тот же угол. Угол поворота представляет собой величину поворота и является угловым аналогом расстояния. Угол поворота ΔθΔθ — это длина дуги, деленная на радиус кривизны.
Угол поворота представляет собой величину поворота и является угловым аналогом расстояния. Угол поворота ΔθΔθ — это длина дуги, деленная на радиус кривизны.
Δθ=ΔсрΔθ=Δср
Угол поворота часто измеряется в радианах. (Радианы на самом деле безразмерны, потому что радиан определяется как отношение двух расстояний, радиуса и длины дуги.) Оборот — это один полный оборот, когда каждая точка на окружности возвращается в исходное положение. Один оборот покрывает 2π2π радиан (или 360 градусов) и, следовательно, имеет угол поворота 2π2π радиан и длину дуги, которая равна длине окружности. Мы можем преобразовать радианы, обороты и градусы, используя соотношение
1 оборот = 2π2πрад = 360°. См. Таблицу 6.1 для преобразования градусов в радианы для некоторых распространенных углов.
6,12π рад=360°1 рад=360°2π≈57,3°2π рад=360°1 рад=360°2π≈57,3°
Таблица 6.1 Обычно используемые углы в градусах и радианах
Угловая скорость
Как быстро вращается объект? Мы можем ответить на этот вопрос, используя понятие угловой скорости. Сначала рассмотрим угловую скорость (ω)(ω) — скорость изменения угла поворота. В форме уравнения угловая скорость равна
6.2ω=ΔθΔt,ω=ΔθΔt,
, что означает, что угловой поворот (Δθ)(Δθ) происходит за время ΔtΔt. Если объект поворачивается на больший угол поворота за заданное время, он имеет большую угловую скорость.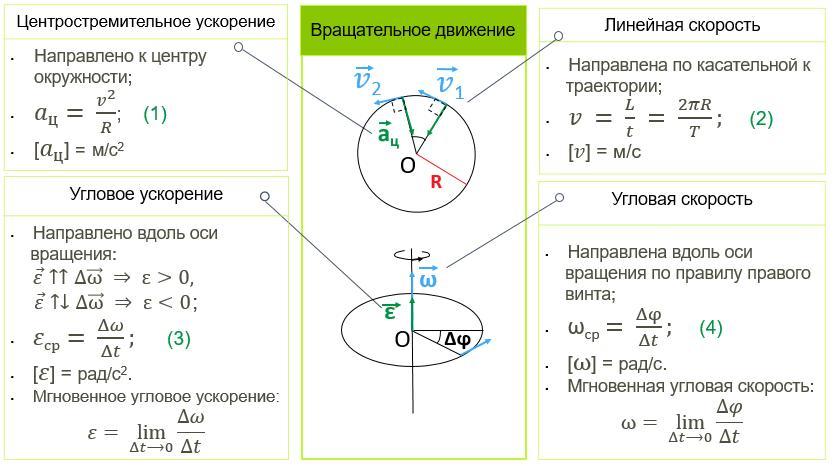 Единицами угловой скорости являются радианы в секунду (рад/с).
Единицами угловой скорости являются радианы в секунду (рад/с).
Теперь давайте рассмотрим направление угловой скорости, а значит мы теперь должны называть его угловой скоростью. Направление угловой скорости вдоль оси вращения. Для объекта, вращающегося по часовой стрелке, угловая скорость направлена от вас вдоль оси вращения. Для объекта, вращающегося против часовой стрелки, угловая скорость указывает на вас вдоль оси вращения.
Угловая скорость (ω) представляет собой угловую версию линейной скорости v . Тангенциальная скорость — это мгновенная линейная скорость объекта во вращательном движении . Чтобы получить точное соотношение между угловой скоростью и тангенциальной скоростью, снова рассмотрим ямку на вращающемся компакт-диске. Эта яма движется по дуге длиной (Δs)(Δs) за короткое время (Δt)(Δt), поэтому ее тангенциальная скорость равна
6.3
v=ΔsΔt.v=ΔsΔt.
Из определения угла поворота Δθ=ΔsrΔθ=Δsr видно, что Δs=rΔθΔs=rΔθ. Подставляя это в выражение для v дает
v=rΔθΔt=rω.v=rΔθΔt=rω.
Уравнение v=rωv=rω говорит, что тангенциальная скорость v пропорциональна расстоянию r от центра вращения. Следовательно, тангенциальная скорость больше для точки на внешнем краю компакт-диска (с большими r ), чем для точки ближе к центру компакт-диска (с меньшими r ). Это имеет смысл, потому что точка, расположенная дальше от центра, должна пройти большую длину дуги за то же время, что и точка, расположенная ближе к центру. Обратите внимание, что обе точки по-прежнему будут иметь одинаковую угловую скорость, независимо от их расстояния от центра вращения. См. рисунок 6.4.
Рисунок 6.4 Точки 1 и 2 поворачиваются на один и тот же угол (ΔθΔθ), но точка 2 перемещается по большей дуге (Δs2Δs2), поскольку она находится дальше от центра вращения.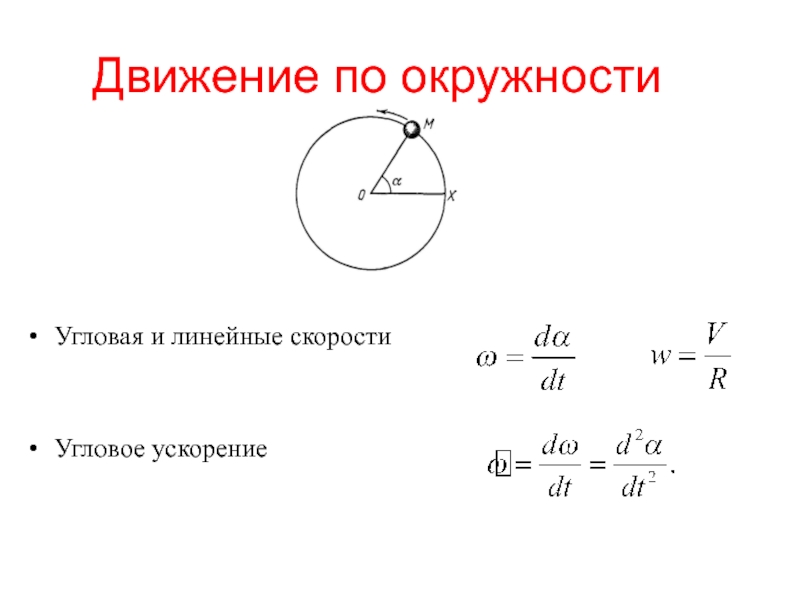
Теперь рассмотрим другой пример: шина движущегося автомобиля (см. рис. 6.5). Чем быстрее вращается шина, тем быстрее движется автомобиль — большое ωω означает большое против , потому что v=rωv=rω. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью ωω, будет производить большую линейную (тангенциальную) скорость в, на машину. Это связано с тем, что больший радиус означает, что более длинная дуга должна касаться дороги, поэтому автомобиль должен двигаться дальше за то же время.
Рис. 6.5 Автомобиль, движущийся со скоростью v, вправо, имеет шину, вращающуюся с угловой скоростью ωω. Скорость протектора шины относительно оси составляет 90 282 v 90 283 , такая же, как если бы автомобиль был поднят на домкрат и колеса крутились, не касаясь дороги. Непосредственно под осью, где шина касается дороги, протектор шины движется назад относительно оси с тангенциальной скоростью v=rωv=rω, где r это радиус шины.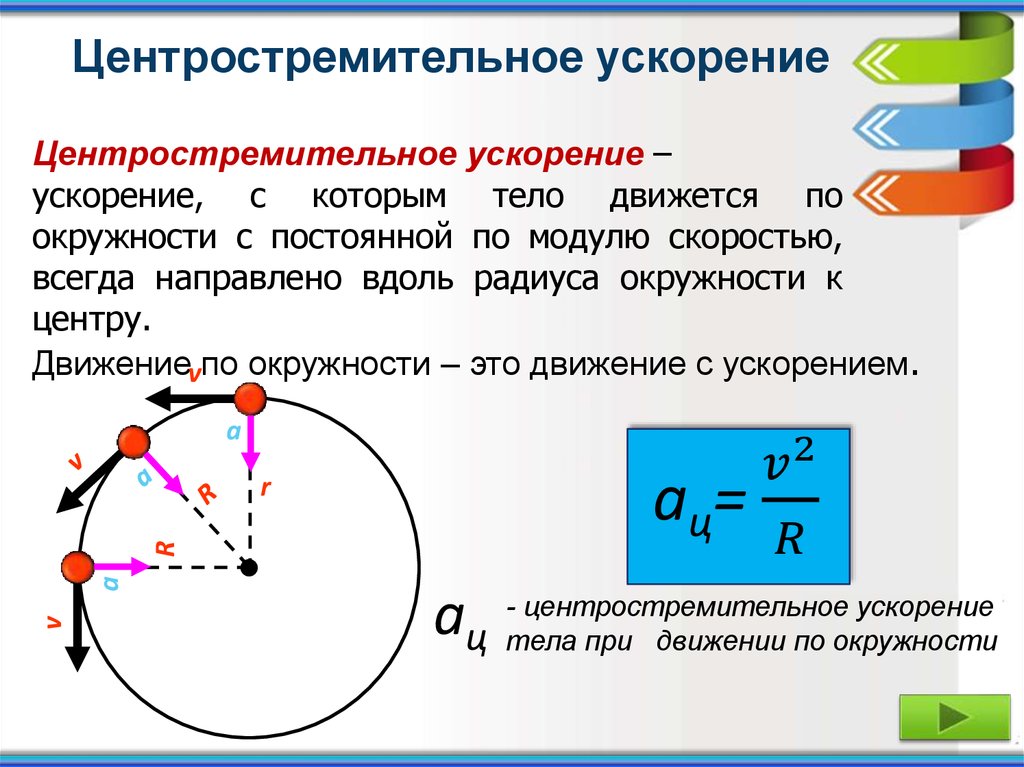 Поскольку дорога неподвижна относительно этой точки шины, автомобиль должен двигаться вперед с линейной скоростью v . Большая угловая скорость шины означает большую линейную скорость автомобиля.
Поскольку дорога неподвижна относительно этой точки шины, автомобиль должен двигаться вперед с линейной скоростью v . Большая угловая скорость шины означает большую линейную скорость автомобиля.
Однако бывают случаи, когда линейная скорость и тангенциальная скорость не эквивалентны, например, когда колеса автомобиля крутятся на льду. В этом случае линейная скорость будет меньше тангенциальной скорости. Из-за отсутствия трения под шинами автомобиля на льду длина дуги, по которой перемещаются протекторы шин, больше, чем линейное расстояние, по которому движется автомобиль. Это похоже на бег на беговой дорожке или вращение педалей на велотренажере; вы буквально никуда не денетесь.
Советы по достижению успеха
Угловая скорость ω и тангенциальная скорость v являются векторами, поэтому мы должны указать величину и направление. Направление угловой скорости находится вдоль оси вращения и указывает от вас для объекта, вращающегося по часовой стрелке, и к вам для объекта, вращающегося против часовой стрелки. В математике это описывается правилом правой руки. Тангенциальная скорость обычно описывается как восходящая, нисходящая, левая, правая, северная, южная, восточная или западная, как показано на рис. 6.6.
В математике это описывается правилом правой руки. Тангенциальная скорость обычно описывается как восходящая, нисходящая, левая, правая, северная, южная, восточная или западная, как показано на рис. 6.6.
Рис. 6.6 Когда муха на краю старой виниловой пластинки движется по кругу, ее мгновенная скорость всегда направлена по касательной к кругу. В этом случае направление угловой скорости находится на странице.
Watch Physics
Взаимосвязь между угловой скоростью и скоростью
В этом видеоролике рассматриваются определение и единицы измерения угловой скорости, а также их связь с линейной скоростью. Он также показывает, как конвертировать между оборотами и радианами.
Проверка захвата
Для объекта, движущегося по круговой траектории с постоянной скоростью, изменится ли линейная скорость объекта при увеличении радиуса траектории?
- Да, потому что тангенциальная скорость не зависит от радиуса.

- Да, потому что тангенциальная скорость зависит от радиуса.
- Нет, так как тангенциальная скорость не зависит от радиуса.
- Нет, так как тангенциальная скорость зависит от радиуса.
Решение задач на угол поворота и угловую скорость
Snap Lab
Измерение угловой скорости
В этом упражнении вы создадите и измерите равномерное круговое движение, а затем сопоставите его с круговыми движениями с разными радиусами.
Материалы
- Одна струна (длиной 1 м)
- Один предмет (резиновая пробка с двумя отверстиями) для привязки к концу
- Один таймер
Процедура
- Привяжите объект к концу нити.
- Раскачивайте объект по горизонтальному кругу над головой (раскачивание с запястья).
 Важно, чтобы круг был горизонтальным!
Важно, чтобы круг был горизонтальным! - Поддерживайте постоянную скорость объекта при его раскачивании.
- Таким образом измерьте угловую скорость объекта. Измерьте время в секундах, за которое объект совершает 10 оборотов. Разделите это время на 10, чтобы получить угловую скорость в оборотах в секунду, которую вы можете преобразовать в радианы в секунду.
- Какова приблизительная линейная скорость объекта?
- Поднимите руку вверх по веревке так, чтобы длина веревки составила 90 см. Повторите шаги 2–5.
- Переместите руку вверх по веревке так, чтобы ее длина составила 80 см. Повторите шаги 2–5.
- Переместите руку вверх по веревке так, чтобы ее длина составила 70 см. Повторите шаги 2–5.
- Переместите руку вверх по веревке так, чтобы ее длина составила 60 см. Повторите шаги 2–5
- Переместите руку вверх по веревке так, чтобы ее длина составила 50 см. Повторите шаги 2–5
- Постройте графики зависимости угловой скорости от радиуса (т.
 е. длины струны) и линейной скорости от радиуса. Опишите, как выглядит каждый график.
е. длины струны) и линейной скорости от радиуса. Опишите, как выглядит каждый график.
Проверка захвата
Если вы медленно качаете объект, он может вращаться со скоростью менее одного оборота в секунду. Каковы были бы обороты в секунду для объекта, который делает один оборот за пять секунд? Какова будет его угловая скорость в радианах в секунду?
- Объект будет вращаться со скоростью 15 об/с. Угловая скорость объекта будет 2π5 рад/с.
- Объект будет вращаться со скоростью 15 об/с. Угловая скорость объекта будет π5 рад/с.
- Объект будет вращаться со скоростью 5 об/с. Угловая скорость объекта будет 10πрад/с.
- Объект будет вращаться со скоростью 5 об/с. Угловая скорость объекта будет 5πрад/с.
Теперь, когда у нас есть понимание концепций угла поворота и угловой скорости, мы применим их к реальным ситуациям башни с часами и вращающейся шины.
Рабочий пример
Угол поворота на башне с часами
Часы на башне с часами имеют радиус 1,0 м. а) На какой угол поворачивается часовая стрелка часов, когда она движется с 12 часов дня до 12 часов дня. до 15:00? (b) Какова длина дуги по внешнему краю часов между часовой стрелкой в эти два времени?
Стратегия
Мы можем вычислить угол поворота, умножив полный оборот (2π2π радиан) на долю 12 часов, покрываемых часовой стрелкой при переходе от 12 к 3. Получив угол поворота, мы можно определить длину дуги, переформулировав уравнение Δθ=ΔsrΔθ=Δsr, поскольку радиус задан.
Решение задачи (a)
При переходе от 12 к 3 часовая стрелка покрывает 1/4 из 12 часов, необходимых для совершения полного оборота. Следовательно, угол между часовой стрелкой в положении 12 и 3 равен 14×2π рад=π214×2π рад=π2 (т. е. 90 градусов).
Решение (б)
Преобразовывая уравнение
6.4Δθ=Δsr,Δθ=Δsr,
получаем
6. 5Δs=rΔθ.Δs=rΔθ.
5Δs=rΔθ.Δs=rΔθ.
Подстановка известных значений дает длину дуги
6,6Δs=(1,0 м)(π2 рад)=1,6 мΔs=(1,0 м)(π2 рад)=1,6 м
Обсуждение
Мы смогли убрать радианы из окончательного решения в части (b), поскольку радианы на самом деле безразмерны. Это связано с тем, что радиан определяется как отношение двух расстояний (радиуса и длины дуги). Таким образом, формула дает ответ в метрах, как и ожидалось для длины дуги.
Рабочий пример
Как быстро вращается автомобильная шина?
Рассчитайте угловую скорость автомобильной шины радиусом 0,300 м, когда автомобиль движется со скоростью 15,0 м/с (около 54 км/ч). Смотрите этот рисунок.
Стратегия
В этом случае скорость протектора шины относительно оси шины равна скорости автомобиля относительно дороги, поэтому мы имеем v = 15,0 м/с. Радиус шины равен r = 0,300 м. Поскольку мы знаем v и r , мы можем изменить уравнение v=rωv=rω, чтобы получить ω=vrω=vr и найти угловую скорость.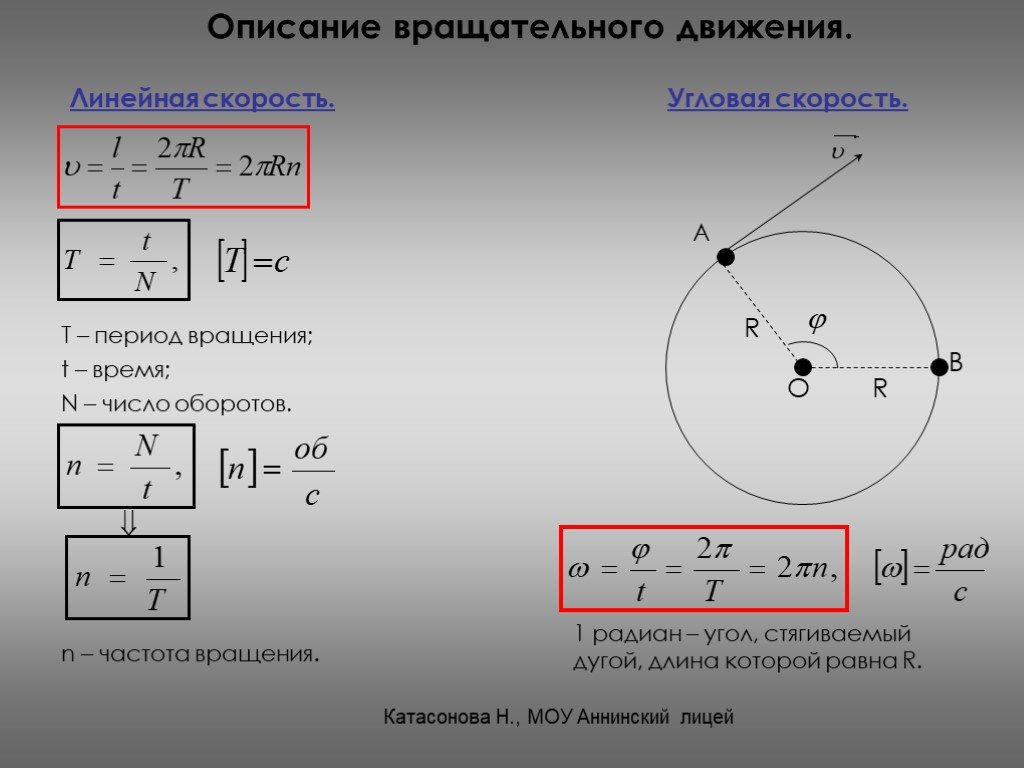
Решение
Для нахождения угловой скорости используем соотношение: ω=vrω=vr.
Вставка известных количеств дает
6,7ω=15,0 м/с0,300 м=50,0 рад/с.ω=15,0 м/с0,300 м=50,0 рад/с.
Обсуждение
Когда мы отбрасываем единицы в приведенном выше расчете, мы получаем 50,0/с (т. е. 50,0 в секунду, что обычно записывается как 50,0 с −1 ). Но угловая скорость должна иметь единицы рад/с. Поскольку радианы безразмерны, мы можем подставить их в ответ для угловой скорости, потому что мы знаем, что движение является круговым. Также обратите внимание, что если бы землеройная машина с колесами гораздо большего размера, скажем, радиусом 1,20 м, двигалась с той же скоростью 15,0 м/с, его колеса вращались бы медленнее. У них будет угловая скорость
6,8ω=15,0 м/с1,20 м=12,5 рад/сω=15,0 м/с1,20 м=12,5 рад/с
Практические задачи
Чему равен угол в градусах между часовой и минутной стрелками часов, показывающих 9 часов утра?
- 0°
- 90°
- 180°
- 360°
Каково приблизительное значение длины дуги между часовой и минутной стрелками часов, показывающих 10:00, если радиус часов равен 0,2 м?
- 0,1 м
- 0,2 м
- 0,3 м
- 0,6 м
Проверьте свое понимание
Упражнение 1
Что такое круговое движение?
- Круговое движение — это движение объекта по линейной траектории.

- Круговое движение — это движение объекта по зигзагообразной траектории.
- Круговое движение — это движение объекта по круговой траектории.
- Круговое движение – это движение объекта по окружности окружности или вращение по круговой траектории.
Упражнение 2
Что подразумевается под радиусом кривизны при описании вращательного движения?
- Радиус кривизны — это радиус кругового пути.
- Радиус кривизны — это диаметр кругового пути.
- Радиус кривизны – это длина окружности кругового пути.
- Радиус кривизны – это площадь кругового пути.
Упражнение 3
Что такое угловая скорость?
- Угловая скорость – это скорость изменения диаметра кругового пути.
- Угловая скорость – это скорость изменения угла, образуемого круговой траекторией.

- Угловая скорость – это скорость изменения площади кругового пути.
- Угловая скорость – это скорость изменения радиуса кругового пути.
Упражнение 4
Какое уравнение определяет угловую скорость ω? Предположим, что r — радиус кривизны, θ — угол, t — время.
- ω=ΔθΔt
- ω=ΔtΔθ
- ω=ΔrΔt
- ω=ΔtΔr
Упражнение 5
Найдите три примера объекта, движущегося по кругу.
- искусственный спутник Земли, гоночный автомобиль, движущийся по круговой гоночной трассе, и волчок, вращающийся вокруг своей оси
- искусственный спутник, вращающийся вокруг Земли, гоночный автомобиль, движущийся по круговой гоночной трассе, и электрон, движущийся по круговой орбите вокруг ядра
- Земля, вращающаяся вокруг своей оси, гоночный автомобиль, движущийся по круговой гоночной трассе, и электрон, движущийся по круговой орбите вокруг ядра.



 Важно, чтобы круг был горизонтальным!
Важно, чтобы круг был горизонтальным! е. длины струны) и линейной скорости от радиуса. Опишите, как выглядит каждый график.
е. длины струны) и линейной скорости от радиуса. Опишите, как выглядит каждый график.

