Содержание

Глава 7. Вращательное движение. Кинематика и динамика

Как правило, в любом варианте задания ЕГЭ по физике представлены несколько задач на вращательное движение. Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью тела, совершающего вращательное движение, называется отношение угла поворота к тому времени , за которое этот поворот произошел


(7.1)

В этом определении угол должен измеряться в радианах, поэтому размерность угловой скорости рад/с (или 1/с поскольку радиан — безразмерная величина). В принципе, определение (7.1) позволяет найти как среднюю (для больших интервалов времени ), так и мгновенную (при ) угловую скорость. Однако в школьном курсе физики рассматривается только движение с постоянной угловой скоростью, для которого определение (7.1) дает один и тот же результат для любых интервалов времени . Применяя определение (7. 1) к полному обороту тела (угол поворота — радиан), получим связь угловой скорости и периода вращения


(7.2)

Угловую скорость можно ввести не только для точечного тела, но и для протяженного тела. Действительно, при вращении неточечного тела вокруг любой оси все его точки поворачиваются за одинаковое время на одинаковый угол. Поэтому можно говорить об угловой скорости всего тела.

Из формулы (7.2) легко получить связь угловой и обычной скорости вращающегося точечного тела (в этом контексте последнюю всегда называют линейной скоростью). Умножая правую и левую часть формулы (7.2) на радиус окружности и учитывая, что – это длина пути, пройденного за период, получим


(7.3)

Конечно, для неточечного вращающегося тела нельзя ввести понятие линейной скорости, поскольку у разных точек этого тела линейные скорости будут разными.

Очевидно, при вращательном движении тело всегда имеет ускорение. Действительно, согласно определению (2.1) ускорение тела равно нулю, если не меняется вектор скорости этого тела (т.е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна


(7.4)

Ускорение (7.3) принято называть центростремительным. Если использовать связь линейной и угловой скорости тела при вращательном движении (7.3), то формулу для центростремительного ускорения можно записать и в таких формах


(7.5)

Согласно второму закону Ньютона ускорения сообщаются телам силами.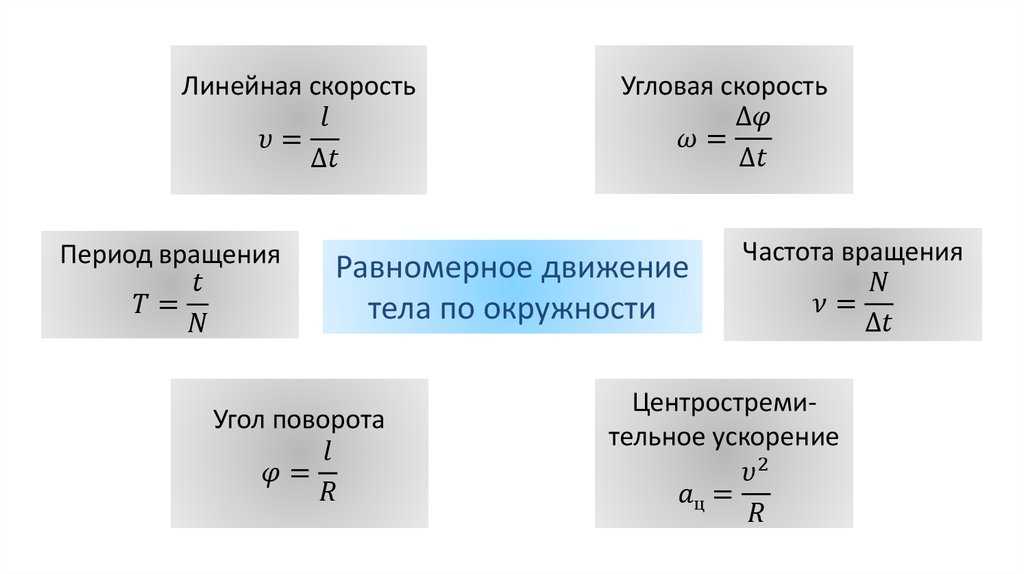 Поэтому если тело совершает движение по окружности радиуса с постоянной по величине скоростью (и соответственно угловой скоростью ), на него должна действовать сила, направленная к центру окружности и равная по величине


(7.6)

Силу (7.6) принято называть центростремительной. Отметим, что термин «центростремительная» связан не с природой этой силы, а с тем, как она действует: в разных ситуациях центростремительной силой может быть и сила тяжести, и сила трения, и сила реакции, и другие силы или их комбинации.

Перечисленных законов и определений достаточно для решения любых задач ЕГЭ на вращательное движение. Рассмотрим их применение к решению задач, приведенных в первой части.

Если период вращения тела задан, то его угловая скорость может быть однозначно определена независимо от размеров тела или радиуса орбиты для точечного тела. В частности, секундная стрелка любых часов поворачивается на угол за одну минуту (конечно, при условии, что они идут «правильно»). Поэтому угловая скорость секундных стрелок любых часов равна рад/мин (задача 7.1.1 – ответ 2).

Для нахождения линейной скорости конца секундной стрелки часов (задача 7.1.2) используем связь угловой и линейной скоростей (7.5). Имеем


(правильный ответ – 2).

Применяя определение угловой скорости к колесу (задача 7.1.3), получаем


(правильный ответ 1).

Из формулы (7.2) имеем


(задача 7.1.4 – правильный ответ 4).

Используя известное расстояние от первой точки до оси вращения и ее центростремительное ускорение (задача 7.1.5), из формулы (7.5) находим квадрат угловой скорости диска


А теперь по формуле (7. 5) для второй точки получаем


(ответ 2).

Поскольку скорость автомобиля в задаче 7.1.6 не меняется в процессе движения для сравнения центростремительных ускорений автомобиля в разных точках траектории следует использовать формулу (7.4), из которой находим, что ускорение тем больше, чем меньше радиус траектории (правильный ответ – 3).

Ускорение мальчика из задачи 7.1.7 будет равно нулю, если его скорость относительно земли будет равна нулю. Поэтому при движении мальчика против движения карусели, его скорость относительно карусели равна скорости карусели относительно земли . Если мальчик пойдет в другую сторону с той же скоростью относительно карусели, его скорость относительно земли будет равна . Поэтому центростремительное ускорение мальчика будет равно


(ответ 4).

Тело, находящееся на поверхности вращающегося диска и вращающееся вместе с ним (задача 7. 1.8), участвует в следующих взаимодействиях. Во-первых, тело притягивается к земле (сила тяжести), и на него действует поверхность диска (сила нормальной реакции и трения), причем сила трения в каждый момент времени направлена к оси вращения (см. рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия. Поэтому правильный ответ на вопрос задачи – 1. Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).

Поскольку тело в задаче 7.1.9 вращается с постоянной по величине скоростью по окружности, то его ускорение направлено к центру окружности, и, следовательно, согласно второму закону Ньютона, туда же направлена и результирующая сила, действующая на тело (ответ 2).

Применяя к данному в задаче 7.1.10 телу второй закон Ньютона и учитывая, что его ускорение равно м/с2, получим для равнодействующей =2 Н (ответ 2).

Используя формулу для центростремительного ускорения , находим отношение ускорений материальных точек из задачи 7.2.1


(ответ 1).

Для сравнения центростремительных ускорений материальных точек в задаче 7.2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем


(ответ 3).

Для сравнения центростремительных ускорений тел в задаче 7. 2.3 выразим ускорение через радиус окружности и период. Используя формулу (7.2) для периода и (7.5) для центростремительного ускорения, получим


(7.5)

Поэтому


(ответ 1).

Используя связь угловой и линейной скорости, находим скорости концов часовой и минутной стрелки (задача 7.2.4)


где и – угловые скорости часовой и минутной стрелки соответственно (в рад/час), и – длины часовой и минутной стрелок. Учитывая, что , получаем


(ответ 2).

Телу, вращающемуся вместе с диском на его горизонтальной поверхности (задача 7.2.5), центростремительное ускорение сообщается силой трения


Поэтому при увеличении угловой скорости вращения диска возрастает и сила трения между телом и диском. При некоторой угловой скорости сила трения достигнет максимально возможного для нее значения . Если еще увеличить угловую скорость диска, сила трения уже не сможет удержать тело на диске: тело начнет скользить по поверхности и слетит с поверхности диска. Поэтому значения угловой скорости, при которой тело может вращаться вместе с диском, находится из неравенства


(ответ 4).

В задаче 7.2.6 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем


(ответ 3).

В задаче 7.2.7 нужно использовать второй закон Ньютона для каждого тела. Силы, действующие на тела, показаны на рисунке. Проекция второго закона Ньютона для дальнего тела на координатную ось, направленную к центру диска, дает


(1)

На ближнее тело действуют силы натяжения и двух нитей (см. рисунок). Поэтому для него из второго закона Ньютона имеем


Подставляя в эту формулу силу из формулы (1), находим (ответ 2).


В задаче 7.2.8 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как и , имеем


где = 1 м/с и = 2 м/с – линейные скорости концов стержня, м – его длина. Решая эту систему уравнений, найдем расстояния и , а затем и угловую скорость стержня . В результате получим


(ответ 3).

Среднее ускорение тела за некоторый интервал времени (не обязательно малый) определяется по формуле (2.1):


где и – скорости тела в конце и начале интервала времени . За половину периода вектор скорости поворачивается на 180°, поэтому величина разности равна . Поэтому среднее ускорение тела за половину периода равно


(задача 7.2.9 – ответ 1).

Очевидно, при зубчатой передаче совпадают линейные скорости точек на ободе шестерней. Действительно, если бы эти скорости были разными, между поверхностями шестерней было бы проскальзывание, которому препятствуют зубцы шестерней (задача 7.2.10 – ответ 2).

Как рассчитывается линейная скорость?

Оглавление

Время чтения: 
4 минуты

647

Интуитивное понятие о скорости мы получаем ещё с детства. Например, глядя в окно или находясь на улице отмечаем про себя, что некоторые из людей идут быстрее, чем другие, а машины на проезжей части движутся быстрее, чем любой из пешеходов. Однако для физики, как науки, такого, бытового понимания о скорости недостаточно, поэтому вводится её точное определение.

Понятие скорости

Скоростью материальной точки (тела) при равномерном движении называется физическая величина, показывающая, какой путь точка (тело), проходит за единицу времени.

Подчеркнём, что речь идёт именно о пути, а не о перемещении. Перемещением называется вектор, соединяющий точку начала и точку конца движения. Его величина равна расстоянию между этими точками. Путь представляет собой длину траектории, по которой происходило движение. Наглядно это можно показать на рисунке.

Рис.1 Красная стрелка – перемещение. Коричневая кривая – путь.

Равномерным движением называют движение, при котором за одинаковые промежутки времени тело проходит одно и то же расстояние. Направление движения при этом может изменяться. В качестве примера можно привести равномерное перемещение точки по окружности.

Формула понятия скорости следующая:

\[\overline{\mathrm{v}}=s / t\]

Чёрточка над \[\overline{\mathrm{v}}\] свидетельство того, что скорость является векторной, т. е. имеющей направление, величиной. Путь s и время t являются скалярными величинами, такими, которые направления в пространстве не имеют.

Чёрточка над \[\overline{\mathrm{v}}\] свидетельство того, что скорость является векторной, т.е. имеющей направление, величиной. Путь s и время t являются скалярными величинами, такими, которые направления в пространстве не имеют.

Из приведённой формулы очень легко найти размерность скорости. Т. к. расстояние измеряется в метрах, а время в секундах, то единицей скорости будет метр в секунду м/с. Отметим, что на практике часто скорость измеряют не в метрах в секунду, а, например, в километрах в час.

Существует ещё так называемая средняя скорость – скалярная величина, равная скорости, с которой бы тело перемещалось, если бы преодолевало путь, двигаясь равномерно.

Примеры

Поезд длиной 300 метров, двигаясь равномерно, проезжает тоннель длиной 420 метров за 3 минуты. Найти скорость поезда.

Решение:
Длину поезда обозначим через l, а длину тоннеля через L.
Словосочетание «проезжает тоннель за 3 минуты» означает, что это время поезд входит в тоннель кабиной машиниста и выходит с концом последнего вагона. Пройденное им расстояние S в таком случае является суммой длины тоннеля и длины поезда.
\[S = I + L = 300 + 420 = 720 м/с.\]
Скорость поезда – это скорость любой из его точек. Для простоты будем считать, что это скорость кабины машиниста.
Переводим минуты в секунды: 3 * 60 = 180с.
Скорость получаем, разделив перемещение на время: 720/180 = 4 м/с.

Ответ: Скорость поезда равна 4 м/с.

Машина 3 часа едет со скоростью 4 км/ч, затем 4 часа со скоростью 61,2 км/ч. Требуется найти среднюю скорость движения машины на всем её пути.

Решение:
Обозначим время движения машины со скоростью 4 км/ч, как \[t_{1}\], а время движения машины со скоростью 61,2 км/ч, как \[t_{2}\].
Находим общий путь, который проехала машина. Обозначим его, как S. Общий равен сумме путей, которые ехала машина со скоростью 58,4 км/ч и 61,2 км/ч. Первый из них обозначим как \[S_{1}\], он равен \[S_{1}\] = 3*58,4 = 175,2 км
Второй из них обозначим как S2, он равен: \[S_{2} = 4*61,2 = 244,8 км\]
Складываем эти расстояния и получаем: S = 175,2 + 244,8 = 420 км
Это есть весь путь, пройденный нашей машиной.
Общее время t, которое она потратила будет \[t = t_{1} + t_{2} =3 + 4 = 7 ч\]
Чтобы узнать среднюю скорость, делим общее расстояние на общее время v = S/t = 420/7 = 60 км/ч.

Ответ: Средняя скорость машины равна 60 км/ч.
Обращать время в секунды, а скорость в метры в секунду здесь смысла не имеет, можно и так получить нужное решение.

Линейная скорость

Линейной скоростью именуют величину равную пути, проходимым телом за единицу времени. Движение тела при этом может быть как прямолинейным так и совершаться по криволинейной траектории, например, окружности. Отметим, что линейная скорость всегда направлена по касательной к траектории.

Формул для расчета линейной скорости существует множество, но общей можно назвать:

\[v=S / t\]

S – путь, который прошло тело, t – время, которое оно на это потратило.

Если тело вращается по окружности, то путь, проходимый им, равен её длине. Как известно из геометрии, указанная величина равна 2πR, где R – радиус окружности. Отсюда легко сообразить, что линейная скорость тела при равномерном движении по окружности будет \[\boldsymbol{v=2 \pi R / T}\].

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

О связи между линейной и угловой скоростями

Угловой скоростью называется векторная величина, показывающая, насколько быстро и в каком направлении вращается материальная точка или тело относительно центра вращения. {2} R\]

Оценить статью (39 оценок):

Поделиться

Окружная скорость лопасти на входе, соответствующая калькулятору диаметра

✖Скорость в об/мин — это количество оборотов объекта, деленное на время, указанное как обороты в минуту (об/мин).ⓘ Скорость в об/мин [Н]

+10%

-10%

AlnAngstromArpentAstronomical UnitAttometerAU of LengthBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (Long)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance from SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedReed (Long) RodRoman ActusВеревкаРусский АрчинПролет (Ткань)Радиус СолнцаТераметрTwipVara CastellanaVara ConuqueraVara De TareaЯрдYoctometerYottameterZeptometerZettameter

+10%

-10%

✖Периферическая скорость на входе — это скорость, с которой точка на окружности движется в секунду. ⓘ Окружная скорость лопасти на входе, соответствующая диаметру [u 1 ]

Сантиметр в часСантиметр в минутуСантиметр в секундуКосмическая скорость перваяКосмическая скорость втораяКосмическая скорость третьяСкорость ЗемлиФут в часФут в минутуФут в секундуКилометр в часКилометр в минутуКилометр в секундуУзелУзел (Великобритания)МахМах (стандарт SI)Метр в часМетр в минутуМетр в секундуМиль в час ДеньМиль в минутуМилль в секундуМиллиметр в секунду ЧасМиллиметр в минутуМиллиметр в секундуМорская миля в деньМорская миля в часСкорость звука в чистой водеСкорость звука в морской воде (20°C и глубина 10 метров)Ярд в часЯрд в минутуЯрд в секунду

⎘ Копировать

👎

Формула

Перезагрузить

👍

Периферическая скорость лопасти на входе, соответствующая решению диаметра

ШАГ 0: Сводка предварительного расчета

ШАГ 1: Преобразование входных данных в базовые единицы

Скорость в об/мин: 58,5 —> преобразование не требуется
Диаметр: 10 метров —> 10 метров преобразование не требуется

ШАГ 2: Вычисление формулы

ШАГ 3: Преобразование результата в единицу измерения выхода

30,6305283725005 Метр в секунду —> Преобразование не требуется

< 8 калькуляторов общей гидродинамики

Окружная скорость лопасти на входе, соответствующая формуле диаметра

Окружная скорость на входе = pi*скорость в об/мин*диаметр/60

и 1 = pi*N*D/60

Что такое Окружная скорость?

Окружная скорость определяется как скорость, с которой точка на окружности движется в секунду. Она имеет как величину, так и направление.

Как рассчитать окружную скорость лопасти на входе, соответствующую диаметру?

Окружная скорость лопасти на входе, соответствующая диаметру, калькулятор использует периферийной скорости на входе = pi*скорость в об/мин*диаметр/60 для расчета периферийной скорости на входе. Периферическая скорость лопасти на входе, соответствующая формуле диаметра, определяется как π, умноженное на произведение скорости ротора на диаметр, деленное на 60. Окружная скорость на входе обозначается u 1 символ.

Как рассчитать окружную скорость лопасти на входе, соответствующую диаметру, с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для периферийной скорости отвала на входе, соответствующей диаметру, введите скорость в об/мин (N) и диаметр (D) и нажмите кнопку расчета. Вот как можно объяснить окружную скорость лопасти на входе, соответствующую расчету диаметра, с заданными входными значениями -> 30,63053 = пи*58,5*10/60 .

Часто задаваемые вопросы

Какая окружная скорость лопасти на входе соответствует диаметру?

Окружная скорость лопасти на входе, соответствующая формуле диаметра, определяется как π, умноженное на произведение скорости ротора на диаметр, деленное на 60, и представляется как u 1 = pi*N*D/60 или Окружная скорость на входе = pi*скорость в об/мин*диаметр/60 . Скорость в об/мин — это количество оборотов объекта, деленное на время, выраженное в оборотах в минуту (об/мин). Диаметр — это прямая линия, проходящая из стороны в сторону через центр тела или фигуры, особенно круга или сферы.

Как рассчитать окружную скорость лопасти на входе, соответствующую диаметру?

Окружная скорость лопасти на входе, соответствующая формуле диаметра, определяется как π, умноженное на произведение скорости ротора на диаметр, деленное на 60, рассчитывается с использованием Окружная скорость на входе = pi*скорость в об/мин*диаметр/60 . Чтобы рассчитать окружную скорость лопасти на входе, соответствующую диаметру, вам нужно скорость в об/мин (N) и диаметр (D) . С помощью нашего инструмента вам нужно ввести соответствующее значение скорости в об/мин и диаметр и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.

Поделиться

Скопировано!

Определение скорости вращения наконечника рабочего колеса и формула

Определение скорости вращения конца рабочего колеса и формула

10692
Взгляды

1
Комментарий

Опубликовано:
16.10.2012

По

Стивен Шмидт

Скорость наконечника / Периферийная скорость

Скорость лезвия (скорость кончика) измеряет, насколько далеко точка на самом внешнем краю лезвия диспергатора проходит за заданный промежуток времени. Возможно, вы помните из первых уроков математики, что длина окружности (периметр) круга равна:

Длина окружности = Π × D

Итак, если мы возьмем лезвие диаметром 1 фут (D) и повернем его на один полный оборот, точка на его лезвии пройдет pi (Π) 3,14 фута.

Путем умножения на об/мин (n) получаем формулу скорости наконечника:

Скорость наконечника = Π × D × n

где:

  • Скорость вращения наконечника — скорость вращения наконечника рабочего колеса (об/мин)
  • D — диаметр рабочего колеса (футы)
  • n — скорость вращения крыльчатки (футов в минуту)

Скорость вращения лопастей высокоскоростного диспергатора составляет 5200 футов в минуту (футов в минуту).

Производители диспергаторов обычно ориентируются на максимальную скорость своих диспергаторов от 4000 до 6000 футов в минуту (футов в минуту). Как и в случае с диаметром лезвия, есть преимущества в изменении скорости кончика этих рассеивающих лезвий. Более высокие скорости наконечника могут обеспечить превосходный помол в трудно диспергируемых продуктах или компенсировать недостаточную текучесть в партиях с высокой вязкостью. Более низкие скорости уменьшат вихрь в партиях с низкой вязкостью.

С точки зрения оператора, одна лопасть может адекватно функционировать в нескольких резервуарах разного диаметра, что требует меньшего вмешательства оператора.

Наш калькулятор скорости наконечника учитывает наиболее распространенные случаи использования уравнения скорости наконечника.

  • Скорость наконечника — расчет скорости наконечника на основе известного диаметра лезвия и числа оборотов в минуту.
  • об/мин — расчет оборотов в минуту, необходимых для достижения желаемой скорости наконечника при известном диаметре лопасти.
  • Масштабирование — согласование скорости наконечника одного миксера со скоростью второго диспергатора с лопастями разного размера.

Калькулятор скорости наконечника

Калькуляторы скорости наконечника, оборотов в минуту и ​​масштабирования