Содержание
Задачи на нахождение КПД тепловых машин с использованием графиков
На этой странице вы узнаете
- В чем прелесть фазовых переходов?
- Что лучше выбрать: Mercedes или BMW?
Люди научились летать в космос, покорять недра Земли и погружаться в глубины океана. Эти и другие достижения возможны благодаря способности извлекать максимум пользы из имеющихся ресурсов,а именно получать тепловую энергию различными доступными способами. Сегодня мы разберем задачи, которые заставят тепловые процессы играть на нашей стороне.
Тепловые машины и их КПД
Рекомендация: перед тем как приступить к выполнению задач неплохо было бы повторить тему «Уравнение состояния идеального газа» . Но ключевую теорию, на которой основано решение задач, сейчас разберем вместе.
| В чем прелесть фазовых переходов? Вспомним, что фазовые переходы — это переход из одного агрегатного состояния в другое. Именно благодаря этому они и стали такими полезными для нас. Например, в ядерных реакторах воду используют в качестве рабочего тела, то есть она нагревается вследствие энергии, полученной из ядерных реакций, доходит до температуры кипения, а затем под большим давлением уже в качестве водяного пара воздействует на ротор генератора, который вращается и дает нам электроэнергию! На этом основан принцип работы атомных электростанций. А самый простой пример фазового перехода — образование льда на лужах в морозные ноябрьские дни. Правда о выделении тепла здесь речи не идет. |
Мы не почувствуем, как испарится капелька у нас на руке, потому что это не требует много тепла от нашего тела. Но мы можем наблюдать, как горят дрова в мангале, когда мы жарим шашлык, потому что выделяется огромное количество теплоты. А зачем мы вообще рассматриваем эти фазовые переходы? Все дело в том, что именно фазовые переходы являются ключевым звеном во всех процессах, где нас просят посчитать КПД, от них нашему рабочему телу и подводится теплота нагревателя.
Человечество придумало такие устройства, которые могут переработать тепловую энергию в механическую.
Тепловые двигатели, или тепловые машины, — устройства, способные преобразовывать внутреннюю энергию в механическую.
Их устройство довольно просто: они на входе получают какую-то энергию (в основном — энергию сгорания топлива), а затем часть этой теплоты расходуется на совершение работы механизмом. Например, в автомобилях часть энергии от сгоревшего бензина идет на движение. Схематично можно изобразить так:
Рабочее тело — то, что совершает работу — принимает от нагревателя количество теплоты Q1, из которой A уходит на работу механизма. Остаток теплоты Q2 рабочее тело отдает холодильнику, по сути — это потеря энергии.
Физика не была бы такой загадочной, если б все в ней было идеально. Как и в любом процессе или преобразовании, здесь возможны потери, зачастую очень большие. Поэтому «индикатором качества» машины является КПД, с которым мы уже сталкивались в механике:
Поэтому «индикатором качества» машины является КПД, с которым мы уже сталкивались в механике:
Коэффициент полезного действия (КПД) тепловой машины — это отношение полезной работы двигателя к энергии, полученной от нагревателя.
| \(\eta = \frac{A}{Q_1}\) , где \(\eta\) — КПД, |
Мы должны понимать, что КПД на практике никогда не получится больше 1, поскольку всегда будут тепловые потери.
Полезную работу можно расписать как Q1 — Q2 (по закону сохранения энергии). Тогда формула примет вид:
| \(\eta = \frac{Q_1 — Q_2}{Q_1} = 1 — \frac{Q_2}{Q_1}\) |
Давайте попрактикуемся в применении данной формулы на задаче номер 9 из ЕГЭ.
Задача. Тепловая машина, КПД которой равен 60%, за цикл отдает холодильнику 100 Дж. Какое количество теплоты за цикл машина получает от нагревателя? (Ответ дайте в джоулях).
Какое количество теплоты за цикл машина получает от нагревателя? (Ответ дайте в джоулях).
Решение:
Давайте сначала вспомним нашу формулу для КПД:
\(\eta = \frac{Q_1 — Q_2}{Q_1}\),
где \(Q_1\) — это теплота, которую тело получает от нагревателя, \(Q_2\) — теплота, которая подводится к холодильнику.
Тогда отсюда можно вывести искомую теплоту нагревателя:
\(\eta Q_1 =Q_1-Q_2\)
\(\eta Q_1 — Q_1= -Q_2\)
\(Q_1=\frac{- Q_2}{\eta-1}=\frac{-100}{0,6-1}=250 Дж\).
Ответ: 250 Дж
Цикл Карно
Мы знаем, что потери — это плохо, поэтому должны предотвращать их. Как это сделать? Нам ничего делать не нужно, за нас уже все сделал Сади Карно, французский физик, разработавший цикл, в котором машины достигают наивысшего КПД. Этот цикл носит его имя и состоит из двух изотерм и двух адиабат. Рассмотрим, как этот цикл выглядит в координатах p(V).
- Температура верхней изотермы 1-2 — температура нагревателя (так как теплота в данном процессе подводится).

- Температура нижней изотермы 3-4 — температура холодильника (так как теплота в данном процессе отводится).
- 2-3 и 4-1 — это адиабатические расширение и сжатие соответственно, в них газ не обменивается теплом с окружающей средой.
Цикл Карно — цикл идеальной тепловой машины, которая достигает наивысшего КПД.
Формула, по которой можно рассчитать ее КПД выражается через температуры:
| \(\eta = \frac{T_1 — T_2}{T_1} = 1 — \frac{T_2}{T_1}\), где T1 — температура нагревателя, |
| Что лучше выбрать: Mercedes или BMW? Не то круто, что красиво, а то, что по Карно работает! Поэтому присматривайте такой автомобиль, у которого высокий КПД. Интересно, что максимальный уровень КПД двигателя внутреннего сгорания автомобилей на данный момент всего около 43%. По официальным заявлениям компания Nissan Motor с 2021 года испытывает прообраз двигателя нового поколения с планируемым КПД 50%. |
Приступим к задачам
Задачи на данную тему достаточно часто встречаются в задании 27 из КИМа ЕГЭ. Давайте разберем некоторые примеры.
Задание 1. Одноатомный газ совершает циклический процесс, как показано на рисунке. На участке 1–2 газ совершает работу A12 = 1520 Дж. Участок 3–1 представляет собой адиабатный процесс. Количество теплоты, отданное газом за цикл холодильнику, равно |Qхол| = 4780 Дж. Найдите работу газа |A13| на адиабате, если количество вещества постоянно.
Решение:
Шаг 1. Первое, с чего лучше начинать задачи по термодинамике — исследование процессов.
Посмотрим на участок 1-2 графика: продолжение прямой проходит через начало координат, поэтому график функционально можно записать, как p = aV, где a — какое-то число, константа. Графиком является не изотерма, поскольку график изотермы в координатах p-V — гипербола. Из уравнения Менделеева-Клапейрона следует: \(\frac{pV}{T} = const\). Отсюда можно сделать вывод, что возрастает температура, так как растут давление и объем. Температура и объем растут, значит, увеличивается и внутренняя энергия и объем соответственно.
Из уравнения Менделеева-Клапейрона следует: \(\frac{pV}{T} = const\). Отсюда можно сделать вывод, что возрастает температура, так как растут давление и объем. Температура и объем растут, значит, увеличивается и внутренняя энергия и объем соответственно.
Участок 2-3: процесс изохорный, поскольку объем постоянен, следовательно, работа газом не совершается. Рассмотрим закон Шарля: \(\frac{p}{T} = const\). Давление в этом процессе растет, тогда растет и температура, поскольку дробь не должна менять свое значение. Делаем вывод, что внутренняя энергия тоже увеличивается.
Участок 3-1: адиабата по условию, то есть количество теплоты в этом переходе равна нулю из определения адиабатного процесса. Работа газа отрицательна, так как газ уменьшает объем.
Оформим все данные в таблицу.
Определим знаки Q, используя первый закон термодинамики: Q = ΔU + A.
Из этих данных сразу видно, что количество теплоты, отданное холодильнику — это количество теплоты в процессе 2-3.
Шаг 2. Первый закон термодинамики для процесса 1-2 запишется в виде:
Q12 = ΔU12 + A12.
Работа A12 — площадь фигуры под графиком процесса, то есть площадь трапеции:
\(A_{12} = \frac{p_0 + 2p_0}{2} * V0 =\frac{3p_0V_0}{2}\).
Запишем изменение внутренней энергии для этого процесса через давление и объем. Мы выводили эту формулу в статье «Первое начало термодинамики»:
\(\Delta U_{12} = \frac{3}{2}(2p_0 * 2V_0 — p_0V_0) = \frac{9p_0V_0}{2}\).
Заметим, что это в 3 раза больше работы газа на этом участке:
\(\Delta U_{12} = 3A_{12} \rightarrow Q_{12} = 4A_{12}\).
Шаг 3. Работа цикла — площадь фигуры, которую замыкает график, тогда . A = A12 — |A31|. С другой стороны, работа цикла вычисляется как разность между энергиями нагревателя и холодильника: A = Q12 — |Q31|.
Сравним эти формулы:
Q12 -|Q31| = A12 — |A31|,
подставим выражения из предыдущего пункта:
4A12 — |Q31| = A12 — |A31| \(\rightarrow\) |A31| = -3A12 + |Q31| = -31520 + 4780 = 220 Дж.
Ответ: 220 Дж
Задание 2. Найти КПД цикла для идеального одноатомного газа.
Решение:
Шаг 1. КПД цикла определим по формуле: \(\eta = \frac{A}{Q}\), где Q — количество теплоты от нагревателя, а А — работа газа за цикл. Найдем А как площадь замкнутой фигуры: A = (2p1 — p1)(3V1 — V1) = 2p1V1.
Шаг 2. Найдем процесс, который соответствует получению тепла от нагревателя. Воспользуемся теми же приемами, что и в прошлой задаче:
Посмотрим на участок 1-2 графика: давление растет, объем не меняется. По закону Шарля \(\frac{p}{T} = const\) температура тоже растет. Работа газа равна 0 при изохорном процессе, а изменение внутренней энергии положительное.
2-3: давление не меняется, растет объем, а значит, работа газа положительна. По закону Гей-Люссака \(\frac{V}{T} = const\) температура тоже растет, растет и внутренняя энергия.
3-4: давление уменьшается, следовательно, и температура уменьшается. При этом процесс изохорный и работа газа равна 0.
4-1: давление не меняется, объем и температура уменьшаются — работа газа отрицательна и внутренняя энергия уменьшается.
Оформим данные в таблицу:
Отметим, что необходимое Q = Q12 + Q23.
Шаг 3. Запишем первый закон термодинамики для процессов 1-2 и 2-3:
\(Q_{12} = U_{12} + A_{12} = \Delta U_{12} = \frac{3}{2}(2p_1V_1 -p_1V_1) = \frac{3}{2}p_1V_1\).
\(Q_{23} = \Delta U_{23} + A_{23}\), работу газа найдем как площадь под графиком: A23 = 2p1(3V1 — V1) = 4p1V1.
\(\Delta U_{12} = \frac{3}{2}(2p_1 * 3V_1 — 2p_1V_1) = 6p_1V_1\).
\(Q_{23} = \Delta U_{23} + A_{23} = 10p_1V_1\).
Шаг 4. Мы готовы считать КПД: \(\eta = \frac{A}{Q} = \frac{A}{Q_{12} + Q_{23}} = \frac{2p_1V_1}{\frac{3}{2}p_1V_1 + 10p_1V_1} = \frac{4}{23} \approx 0,17\).
Ответ: 17%
Теперь вас не должно настораживать наличие графиков в условиях задач на расчет КПД тепловых машин. Продолжить обучение решению задач экзамена вы можете в статьях «Применение законов Ньютона» и «Движение точки по окружности».
Фактчек
- Тепловые двигатели — устройства, способные преобразовывать внутреннюю энергию в механическую.
- Тепловая машина принимает тепло от нагревателя, отдает холодильнику, а рабочим телом совершает работу.
- Коэффициент полезного действия (КПД) тепловой машины — это отношение полезной работы двигателя к энергии, полученной от нагревателя.
\(\eta = \frac{A}{Q_1} = \frac{Q_1 — Q_2}{Q_1} = 1 — \frac{Q_2}{Q_1}\) - Цикл Карно — цикл с максимально возможным КПД: \(\eta = \frac{T_1 — T_2}{T_1} = 1 — \frac{T_2}{T_1}\)
- Не забываем, что работа считается, как площадь фигуры под графиком.
Проверь себя
Задание 1.
1 моль идеального газа переходит из состояния 1 в состояние 2, а потом — в состояние 3 так, как это показано графике. Начальная температура газа равна T0 = 350 К. Определите работу газа при переходе из состояния 2 в состояние 3, если k = 3, а n = 2.
- 5672 Дж
- 4731 Дж
- 5817 Дж
- 6393 Дж
Задание 2.
1 моль идеального одноатомного газа совершает цикл, который изображен на pV-диаграмме и состоит из двух адиабат, изохоры, изобары. Модуль отношения изменения температуры газа при изобарном процессе ΔT12 к изменению его температуры ΔT34 при изохорном процессе равен 1,5. Определите КПД цикла.
- 0,6
- 0,5
- 0,8
- 1
Задание 3.
В топке паровой машины сгорело 50 кг каменного угля, удельная теплота сгорания которого равна 30 МДж/кг. При этом машиной была совершена полезная механическая работа 135 МДж. Чему равен КПД этой тепловой машины? Ответ дайте в процентах.
Чему равен КПД этой тепловой машины? Ответ дайте в процентах.
- 6%
- 100%
- 22%
- 9%
Задание 4.
С двумя молями одноатомного идеального газа совершают циклический процесс 1–2–3–1 (см. рис.). Чему равна работа, совершаемая газом на участке 1–2 в этом циклическом процессе?
- 4444 Дж
- 2891 Дж
- 4986 Дж
- 9355 Дж
Ответы:1 — 3; 2 — 1; 3 — 4; 4 — 3.
26. Кпд тепловых машин, работа газа (в)
I:
26.01; t=0; k=В; ek=50; m=50; c=0;
S:
Цикл Карно состоит …
-:
из двух изотерм и двух изохор
-:
из двух изотерм и двух изобар
+:
из двух изотерм и двух адиабат
-:
из двух изобар и двух адиабат
-:
из двух изохор и двух адиабат
I:
26.02; t=0; k=В; ek=50; m=50; c=0;
S:
В идеальном тепловом двигателе абсолютная
температура холодильника в 5
раз меньше абсолютной температуры
нагревателя. КПД такого двигателя равен
КПД такого двигателя равен
…
-:
20 %
-:
100 %
+:
80 %
-:
50 %
-:
70 %
I:
26.03; t=0; k=В; ek=50; m=50; c=0;
S:
Идеальная тепловая машина за цикл
совершает работу 20
Дж.
КПД тепловой машины равен 40
%
. Количество теплоты, отданное холодильнику
равно …
-:
50 Дж
-:
20 Дж
+:
30 Дж
-:
70 Дж
-:
100 Дж
I:
26.04; t=0; k=В; ek=50; m=50; c=0;
S:
Если
идеальный тепловой двигатель, получив
200
Дж
теплоты от нагревателя при температуре
167С
, совершил работу 50
Дж,
то температура холодильника (С)
равна
+:
57
-:
110
-:
125
-:
150
-:
100
I:
26. 05; t=0; k=В; ek=50; m=50; c=0;
05; t=0; k=В; ek=50; m=50; c=0;
S:
В
идеальном тепловом двигателе абсолютная
температура холодильника в 5
раз меньше абсолютной температуры
нагревателя. Каким станет КПД этого
двигателя, если, не меняя температуры
холодильника, понизить температуру
нагревателя на 25%?
-:
0,67
+:
0,73
-:
0,83
-:
0,50
-:
0,25
I:
26.06; t=0; k=В; ek=50; m=50; c=0;
S:
В
идеальном тепловом двигателе за счёт
каждых 1200
Дж
энергии, полученной от нагревателя,
производится работа, равная 400
Дж.
Во сколько раз абсолютная температура
нагревателя больше абсолютной температуры
холодильника?
+:
1,5
-:
1,7
-:
1,2
-:
2,0
-:
2,5
I:
26.07; t=0; k=В; ek=50; m=50; c=0;
S:
Температура
струи, выходящей из сопла ракетного
двигателя, равна 1000
К.
Теоретически, КПД этого двигателя может
достичь значения в 70%.
Чему равна температура (K)
в его камере сгорания?
+:
3300
-:
3000
-:
1430
-:
700
-:
1750
I:
26.08; t=0;
k=В;
ek=50;
m=50;
c=0;
S:
Если количество теплоты, отдаваемое
рабочим телом холодильнику, увеличится
в 2
раза, то КПД тепловой машины…
+:
уменьшится на Q2
/ Q1
-:
увеличится на Q2
/ Q1
-:
уменьшится на Q2
/ 2Q1
-:
увеличится на Q2
/ 2Q1
-:
не изменится
I:
26.09; t=0;
k=В;
ek=50;
m=50;
c=0;
S:
Диаграмма циклического процесса
идеального одноатомного газа представлена
на рисунке. Отношение работы за весь
цикл к работе при охлаждении газа равно…
-:
3
-:
2,5
-:
2
+:
1,5
-:
5
I:
26. 10; t=0; k=В; ek=50; m=50; c=0;
10; t=0; k=В; ek=50; m=50; c=0;
S:
Диаграмма циклического процесса
идеального одноатомного газа представлена
на рисунке. Работа циклического процесса
равна…
-:
30 кДж
-:
15 кДж
-:
20 кДж
+:
90 кДж
-:
60 кДж
I:
26.11; t=0;
k=В;
ek=50;
m=50;
c=0;
S:
На диаграмме (p,
V)
изображен цикл Карно для идеального
газа.
Сравните
модули работ, совершаемых на участках
2-3 и 4-1.
+:
АI
= АII
-:
невозможно сравнить
-:
АI
> АII
-:
АI
< АII
I:
26.12; t=0; k=В;
ek=50; m=50; c=0;
S:
Идеальная тепловая машина за цикл
совершает работу 50
Дж
и отдает холодильнику количество
теплоты, равное 100
Дж.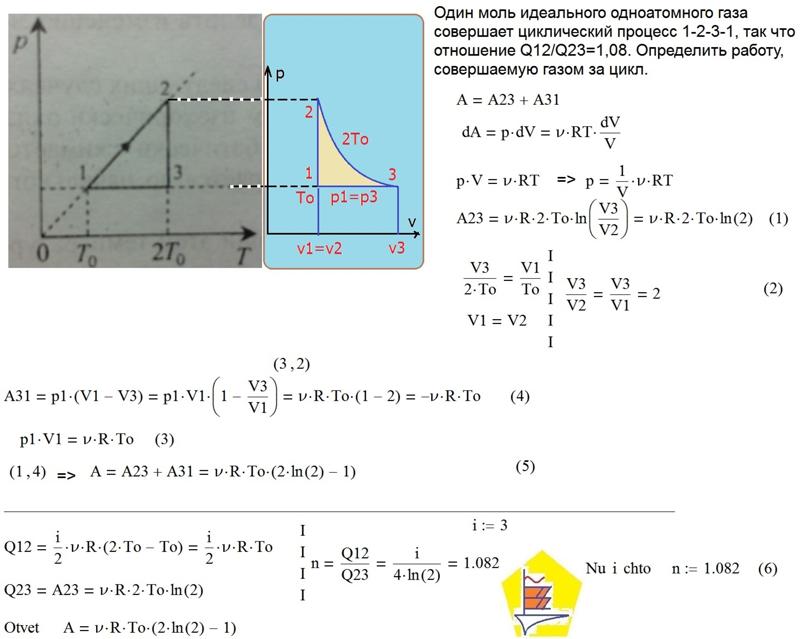
КПД тепловой машины равен …
-:
100 %
-:
50 %
+:
33 %
-:
67 %
-:
40%
I:
26.13; t=0;
k=В;
ek=50;
m=50;
c=0;
S:
КПД
идеальный тепловой машины, работающей
по циклу Карно, равен 30%.
Какую полезную работу (Дж)
совершает машина за цикл, если холодильнику
при этом передаётся 1400
Дж
теплоты?
-:
500
+:
600
-:
650
-:
1200
-:
300
I:
26.14; t=0;
k=В;
ek=50;
m=50;
c=0;
S:
В
камере сгорания ракетного двигателя
температура равна 3000
К.
Коэффициент полезного действия двигателя
при этом теоретически может достигнуть
70%.
Определите температуру газовой струи
(K),
вылетающей из сопла двигателя.
-:
10 000
-:
2100
+:
900
-:
700
-:
300
I:
26. 15; t=0;
15; t=0;
k=В;
ek=50;
m=50;
c=0;
S:
Диаграмма циклического процесса
идеального одноатомного газа представлена
на рисунке. Отношение работы за весь
цикл к работе при нагревании газа равно…
-:
3
-:
2,5
-:
2
-:
1,5
+:
0,6
Тепловые двигатели и холодильники
Тепловые двигатели и холодильники
Для преобразования теплоты в работу необходимо как минимум два места
с разными температурами. Если вы возьмете в Q максимум в
температура T высокая необходимо сбросить как минимум Q низкая при
температура T низкая . Объем работы, которую вы получаете от
тепловой двигатель W = Q высокий — Q низкий . Максимальный объем работы, который вы можете получить от
тепловой двигатель это сумма, которую вы получите
из реверсивного двигателя.
Вт макс. = (Q высокий — Q низкий ) реверсивный
= Q высокий — Q высокий T низкий /T высокий
= Q старший (1 — T низкий /T высокий ).
W является положительным, если T high больше T low .
КПД тепловой машины
отношение полученной работы к затраченной тепловой энергии
температура, e = W/Q высокий . Максимально возможное
КПД е макс такого двигателя
e макс = W макс /Q высокий = (1 — T низкий
/T старший ) = (T высокий — T низкий )/T высокий .
Паровые двигатели
Паровая машина — разновидность тепловой машины. Он забирает тепло от
горячий пар, преобразует часть этого тепла в полезную работу и сбрасывает
отдохнуть на более холодном окружающем воздухе. Максимальная доля тепла
которые можно превратить в работу, можно найти, используя законы
термодинамики, и она увеличивается с разницей температур между
горячий пар и окружающий воздух. Чем горячее пар и
чем холоднее воздух, тем эффективнее паровая машина при преобразовании
тепло в работу.
В типичном паровом двигателе поршень движется вперед и назад внутри
цилиндр. В котле вырабатывается горячий пар высокого давления.
этот пар поступает в цилиндр через клапан. Однажды внутри
цилиндр, пар выталкивается наружу на каждую поверхность, включая
поршень. Поршень движется. Пар совершает механическую работу над
поршень, а поршень совершает механическую работу над присоединенными механизмами
к этому. Расширяющийся пар передает часть своей тепловой энергии
это оборудование, так что пар становится холоднее, когда оборудование работает.
Когда поршень достигает конца своего диапазона, клапан останавливает
поток пара и открывает цилиндр для наружного воздуха.
после этого поршень может легко вернуться. Во многих случаях допускается использование пара.
введите другой конец цилиндра так, чтобы пар толкал поршень
вернуться в исходное положение. Как только поршень вернется в исходное положение
начальной точки, клапан снова впускает пар высокого давления в
цилиндр и весь цикл повторяется. В общем, тепло идет.
В общем, тепло идет.
от горячего котла к более прохладному окружающему воздуху и части этого тепла
преобразуется в механическую работу движущимся поршнем.
максимальный КПД паровой машины e max = (T пар
— T воздух )/T пар . Фактическая эффективность
обычно намного ниже.
Внешняя ссылка: Паровоз (Youtube)
Проблема:
Максимум
возможный КПД паровой машины, принимающей теплоту при 100 o C
и сброс его при комнатной температуре примерно 20 o C?
Решение:
- Обоснование:
Максимальный КПД любой тепловой машины равен КПД двигателя Карно. e max = (T высокий — T низкий )/T высокий . - Детали расчета:
100 o C = 373 K и 20
o С = 293 К.
максимально возможная эффективность
(T высокий — T низкий )/T высокий
= (373 —
293)/373 = 0,21 = 21%.
Двигатели внутреннего сгорания
Двигатель внутреннего сгорания сжигает смесь топлива и воздуха.
Наиболее распространенным типом является четырехтактный двигатель. Поршень скользит в
и из цилиндра. Два или более клапана позволяют топливу и
воздух для входа в цилиндр и газы, которые образуются, когда топливо и воздух
сжечь, чтобы покинуть цилиндр. Когда поршень скользит вперед и назад
внутри цилиндра изменяется объем, который могут занимать газы
кардинально.
Процесс преобразования теплоты в работу начинается, когда поршень
вытащили из цилиндра, расширив замкнутое пространство и позволив
топливо и воздух поступают в это пространство через клапан. Это движение
называется тактом впуска или тактом впуска . Далее топливо и
воздушная смесь сжимается, вдавливая поршень в
цилиндр. Это называется сжатием .
ход . В конце такта сжатия при
топливно-воздушная смесь сжата максимально плотно, свеча зажигания
в запаянном конце цилиндра срабатывает и воспламеняет смесь.
Горячее горящее топливо имеет огромное давление и толкает поршень.
из цилиндра. это рабочий ход — это то, что обеспечивает мощность двигателя и навесного оборудования.
Наконец, сгоревший газ выдавливается из цилиндра через другой
клапан в такте выпуска .
Эти четыре удара повторяются снова и снова. Самый внутренний
двигатели внутреннего сгорания имеют не менее четырех цилиндров и поршней. Там
всегда хотя бы один цилиндр проходит рабочий такт, и это
может нести другие цилиндры через нерабочие такты.
максимальный КПД такого двигателя е max = (T зажигание
— T воздух )/T зажигание где T зажигание
— температура топливно-воздушной смеси после воспламенения. К
максимизировать эффективность использования топлива, вы должны создать максимально горячую
топливно-воздушной смеси после зажигания. Самая высокая эффективность, которая
было достигнуто примерно 50% e max .
Внешняя ссылка: Внутреннее сгорание
двигатель (Ютуб)
Проблема:
Тепловая машина поглощает 360 Дж тепловой энергии и совершает 25 Дж работы в
каждый цикл. Найти
Найти
(а) КПД двигателя и
б) тепловая энергия, выделяемая в каждом цикле.
Решение:
- Обоснование:
Количество работы, которую вы получаете от тепловой машины, равно W = Q высокое — Q низкое .
КПД e = W/Q высокий . - Детали расчета:
Q высокий = 360 Дж. W = 25 Дж. Q низкий
= Q высокая — W = 335
J.
(a) Эффективность e = W/Q высокая = 6,9%.
(b) Излучаемая тепловая энергия Q низкая
= 335 Дж.
Теплота сама по себе не может течь от холодного объекта к горячему — это один из способов сформулировать второй
закон термодинамики. Если бы мог, то сбрасывал тепло на Т низкий
могли просто стекать обратно в водохранилище на Т высокий и сеть
эффектом будет количество тепла ΔQ = Q высокое — Q низкое
взято на Т хай и преобразовано в работу ни с чем другим
изменения в системе.
Предположим, вы хотите отобрать тепло из места с низкой температурой и сбросить
это в месте с более высокой температурой T и высокой . Вы хотите
построить холодильник или
кондиционер . Для
такое устройство мы определяем коэффициент
производительность КПД как отношение количества тепла, отводимого при
более низкая температура работы, вложенной в систему (т.е.
двигатель).
COP = Q низкий /(-W) = Q низкий /(Q высокий
— Q низкий ).
Наилучший возможный коэффициент полезного действия
COP макс. = Q низкий /(Q высокий
— Q низкий ) макс = Q младшая /(Q младшая (T высшая /T младшая ) — Q младшая ) = T младшая /(T высшая — T
3 младшая), 1
младшая
, если у нас есть реверсивный двигатель, перемещающий тепло. Для настоящего
Для настоящего
двигатель Q high больше, чем Q low T high /T low ,
и коэффициент полезного действия меньше.
Для холодильника, поддерживающего внутреннюю температуру 4 o С =
277 K в помещении при 22 o C = 299 K наилучшее возможное
коэффициент полезного действия COP max = 277/(299 — 277) =
12.6. Наилучшее соотношение количества отводимой теплоты к
проделанная работа равна 12,6. Тепло не может течь изнутри обычного
холодильник в более теплое помещение, если мы не подключим электродвигатель
который работает на хладагенте.
Кондиционер — это холодильник, внутри которого находится охлаждаемое помещение (T номер
= T низкий ) и чья внешняя сторона — это великолепная природа (T внешняя
= T высокий ). В кондиционере используется материал
называют «рабочей жидкостью» для передачи тепла из помещения в
свежий воздух. Рабочая жидкость – это материал, который преобразует
Рабочая жидкость – это материал, который преобразует
легко из газа в жидкость и наоборот в широком диапазоне
температуры и давления. Эта рабочая жидкость движется через
три основных компонента кондиционера, компрессор ,
конденсатор ,
и испаритель в непрерывном цикле.
- Рабочая жидкость поступает в испаритель внутри помещения в виде
жидкость низкого давления примерно при температуре наружного воздуха. - Испаритель обычно представляет собой змеевидную трубу. Жидкость
немедленно начинает испаряться и превращается в газ. В процессе
поэтому он использует свою тепловую энергию, чтобы отделить свои молекулы от одного
другой и становится очень холодно. Тепло поступает из помещения в
этот холодный газ. Рабочая жидкость покидает испаритель в виде
газ низкого давления немного ниже комнатной температуры и направляется в сторону
компрессор. - Поступает в компрессор в виде газа низкого давления
примерно при комнатной температуре. Компрессор сжимает молекулы
Компрессор сжимает молекулы
этого газа ближе друг к другу, увеличивая плотность и давление газа.
Поскольку сжатие газа связано с физической работой, компрессор передает
энергию рабочей жидкости, и эта жидкость становится более горячей.
рабочая жидкость выходит из компрессора в виде газа под высоким давлением значительно выше
наружная температура воздуха. - Затем рабочая жидкость поступает в
конденсатор снаружи, который обычно представляет собой змеевидную трубу.
Так как жидкость горячее окружающего воздуха, тепло уходит из
жидкости и в воздух. Затем жидкость начинает конденсироваться в
жидкость и отдает дополнительную тепловую энергию при конденсации.
Эта дополнительная тепловая энергия также передается в виде тепла в наружный воздух.
Рабочая жидкость выходит из конденсатора в виде жидкости под высоким давлением при
примерно температура наружного воздуха. Затем он протекает через
сужение трубы в испаритель. Когда жидкость идет
через сужение в трубе давление в ней падает и она попадает в
испарителя в качестве жидкости низкого давления. Цикл повторяется.
Цикл повторяется.
В целом тепло отводится из помещения и доставляется в
наружный воздух. Компрессор при этом потребляет электроэнергию.
процесс, и эта энергия также становится тепловой энергией в наружном воздухе.
Максимальный коэффициент такого кондиционера КПД max
= T комната /(T снаружи — T комната ).
Холодильники и тепловые насосы работают по одному и тому же принципу.
А тепловой насос — это холодильник, чей
внутри — это великолепная природа, а снаружи — комната, которую нужно отапливать.
коэффициент полезного действия теплового насоса – это отношение отдаваемой энергии
при более высокой температуре работы, вложенной в систему, COP = Q высокий / (Q высокий
— Q низкий ). Наилучший возможный коэффициент полезного действия
COP макс. (тепловой насос) = (Q высокий /(Q высокий
— Q низкий )) макс.
= T высокий /(T высокий — T низкий ) = T комнатный /(T комнатный
— Т снаружи )
Если наружная температура равна 41 o F = 5 o C = 278 K и
комнатная температура 77 o F = 25 o C = 298K, тогда COP макс.
= 298/(298 — 278) = 14,9. Однако, если температура наружного воздуха опустится до 14
или F = -10 или C = 263 K, тогда E max = 298/(298 — 263) = 8,5.
Примечание: КПД холодильника/кондиционера и
КПД теплового насоса определяются по-разному. Мы
всегда интересуются, сколько работы мы должны сделать или сколько полезной энергии
мы должны инвестировать, чтобы чего-то добиться. Для холодильника или воздуха
кондиционер нас интересует насколько эффективно отводится тепло от более холодного
внутри за заданный объем выполненной работы. Для теплового насоса нас интересует
в том, насколько эффективно тепло доставляется к более горячему внутри для данного количества
работа выполнена. Коэффициент полезного действия дает нам эти соотношения.
Коэффициент полезного действия дает нам эти соотношения.
Внешняя ссылка:
цикл охлаждения (Youtube)
Проблема:
Какой КПД холодильника, работающего с
Эффективность Карно между температурами от -3 o C и 27 o C?
Решение:
- Обоснование:
Для холодильника COP max
= T младшая /(T младшая — T младшая ). - Детали расчета:
Наилучший возможный коэффициент полезного действия
COP макс.
= T младшая /(T младшая — T младшая ) =
270/(300 — 270) = 9,
Проблема:
Холодильник имеет коэффициент полезного действия, равный 5. Если
холодильник поглощает 120 Дж тепловой энергии из холодного резервуара в каждом
цикл, найти
(a) работу, выполненную в каждом цикле и
б) тепловая энергия, отводимая в горячий резервуар.
Решение:
- Обоснование:
Для холодильника коэффициент полезного действия COP = Q low /(-Вт).
- Детали расчета:
(a) COP = Q low /(-W). (-W) = Q низкий /COP = 120/5 Дж = 24
Дж.
Работа выполняется в системе. Упорядоченная (электрическая) энергия
преобразуется в тепловую энергию.
(b) (-W) = 24 J = Q высокий — Q низкий . Q высокий
=
24 Дж + 120 Дж = 144 Дж.
Встроенный вопрос 2
Выходная мощность теплового насоса больше, чем энергия, используемая для работы
насос. Почему это утверждение не нарушает первый закон
термодинамика?
Обсудите это со своими однокурсниками на дискуссионном форуме!
4.5 Цикл Карно – University Physics Volume 2
Глава 4. Второй закон термодинамики
Цели обучения
- Описать цикл Карно с ролями всех четырех задействованных процессов
- Опишите принцип Карно и его последствия
- Продемонстрировать эквивалентность принципа Карно и второго закона термодинамики
В начале 1820-х годов французский инженер Сади Карно (1786–1832 гг. ) заинтересовался повышением эффективности практических тепловых двигателей. В 1824 году его исследования привели его к предложению гипотетического рабочего цикла с максимально возможной эффективностью между теми же двумя резервуарами, известного сейчас как 9-й.0015 Цикл Карно . Двигатель, работающий в этом цикле, называется двигателем Карно . Цикл Карно имеет особое значение по целому ряду причин. На практическом уровне этот цикл представляет собой обратимую модель для паровой электростанции и холодильника или теплового насоса. Тем не менее, он также очень важен теоретически, поскольку он играет важную роль в развитии другого важного утверждения второго закона термодинамики. Наконец, поскольку в его работе участвуют только два резервуара, его можно использовать вместе со вторым законом термодинамики для определения шкалы абсолютной температуры, которая действительно не зависит от какого-либо вещества, используемого для измерения температуры.
) заинтересовался повышением эффективности практических тепловых двигателей. В 1824 году его исследования привели его к предложению гипотетического рабочего цикла с максимально возможной эффективностью между теми же двумя резервуарами, известного сейчас как 9-й.0015 Цикл Карно . Двигатель, работающий в этом цикле, называется двигателем Карно . Цикл Карно имеет особое значение по целому ряду причин. На практическом уровне этот цикл представляет собой обратимую модель для паровой электростанции и холодильника или теплового насоса. Тем не менее, он также очень важен теоретически, поскольку он играет важную роль в развитии другого важного утверждения второго закона термодинамики. Наконец, поскольку в его работе участвуют только два резервуара, его можно использовать вместе со вторым законом термодинамики для определения шкалы абсолютной температуры, которая действительно не зависит от какого-либо вещества, используемого для измерения температуры.
С идеальным газом в качестве рабочего тела этапы цикла Карно, представленные на рис. 4.11, следующие.
4.11, следующие.
- Изотермическое расширение. Газ находится в тепловом контакте с тепловым резервуаром при температуре [латекс] {T} _ {\ text {h}}. [/latex] Газ поглощает тепло [латекс] {Q} _ {\ text {h }}[/latex] из теплового резервуара, и ему позволяют изотермически расширяться, совершая работу [латекс]{W}_{1}.[/latex] Поскольку внутренняя энергия [латекс]{E}_{\text{int }}[/latex] идеального газа является функцией только температуры, изменение внутренней энергии равно нулю, то есть [latex]\text{Δ}{E}_{\text{int}}= 0[/latex] во время этого изотермического расширения. Согласно первому закону термодинамики [латекс]\текст{Δ}{E}_{\text{int}}=QW,[/latex] мы находим, что теплота, поглощаемая газом, равна
[латекс] {Q} _ {\ text {h}} = {W} _ {1} = nR {T} _ {\ text {h}} \ phantom {\ rule {0.2em} {0ex}} \ text{ln}\frac{{V}_{N}}{{V}_{M}}.[/latex]
Рисунок 4.11 Четыре процесса цикла Карно. В качестве рабочего тела предполагается идеальный газ, термодинамическая траектория которого MNOP представлена на рис.
 {\gamma}=\phantom{\rule{0.2em}{0ex}}\text{constant}[/latex] и уравнения состояния для идеальный газ, [латекс]pV=nRT[/латекс], имеем 9{\gamma-1}.[/латекс]
{\gamma}=\phantom{\rule{0.2em}{0ex}}\text{constant}[/latex] и уравнения состояния для идеальный газ, [латекс]pV=nRT[/латекс], имеем 9{\gamma-1}.[/латекс] - Изотермическое сжатие . Газ находится в тепловом контакте с холодным резервуаром при температуре [латекс]{Т}_{\текст{с}}[/латекс] и подвергается изотермическому сжатию. В ходе этого процесса над газом совершается работа [латекс]{W}_{3}[/латекс] и он отдает тепло [латекс]{Q}_{\text{с}}[/латекс] холоду. резервуар. Рассуждения, использованные на шаге 1, теперь дают
[латекс]{Q}_{\text{c}}=nR{T}_{\text{c}}\phantom{\rule{0.2em}{0ex}}\ text{ln}\frac{{V}_{O}}{{V}_{P}},[/latex]
где [latex]{Q}_{\text{c}}[/latex] — тепло, отдаваемое газом холодному резервуару.
- Адиабатическое сжатие . Газ термически изолирован и возвращается в исходное состояние за счет сжатия. В этом процессе над газом совершается работа [латекс]{W}_{4}[/латекс]. Поскольку сжатие адиабатическое, температура газа повышается от [латекса] {T} _ {\ text {c}} \ phantom {\ rule {0,2em} {0ex}} \ text {to} \ phantom {\ rule{0.
 2em}{0ex}}{T}_{\text{h}}[/latex] в данном конкретном случае. Обоснование шага 2 теперь дает 9{\gamma-1}.[/латекс]
2em}{0ex}}{T}_{\text{h}}[/latex] в данном конкретном случае. Обоснование шага 2 теперь дает 9{\gamma-1}.[/латекс]Полная работа, выполненная газом в цикле Карно, равна
[латекс]W={W}_{1}+{W}_{2}-{W}_{3}-{W}_{4}.[/latex]
Эта работа равна площади, ограниченной контуром, показанным на диаграмме pV на рис. 4.12. Поскольку начальное и конечное состояния системы одинаковы, изменение внутренней энергии газа в цикле должно быть равно нулю, то есть [латекс]\текст{Δ}{Е}_{\текст{int} }=0[/латекс]. Тогда первый закон термодинамики дает
[латекс] W = Q- \ text {Δ} {E} _ {\ text {int}} = \ left ({Q} _ {\ text {h}} — {Q} _ {\ text {c} }\справа)-0,[/латекс]
и
[латекс] W = {Q} _ {\ text {h}} — {Q} _ {\ text {c}}. [/latex]
Чтобы найти эффективность этой машины, мы сначала разделим [латекс] {Q} _ {\ текст {с}} \ фантом {\ правило {0.2em} {0ex}} \ текст {на} \ фантом {\ правило { 0.2em}{0ex}}{Q}_{\text{h}}:[/latex]
[латекс]\frac{{Q}_{\text{c}}}{{Q}_{\text{h}}}=\frac{{T}_{\text{c}}}{{ T} _ {\ text {h}}} \ phantom {\ rule {0. 2em} {0ex}} \ frac {\ text {ln} {V} _ {O} \ text{/}{V} _ {P }}{\text{ln}{V}_{N}\text{/}{V}_{M}}.[/latex]
2em} {0ex}} \ frac {\ text {ln} {V} _ {O} \ text{/}{V} _ {P }}{\text{ln}{V}_{N}\text{/}{V}_{M}}.[/latex]
Когда постоянная адиабаты из шага 2 делится на постоянную из шага 4, мы находим
[латекс]\frac{{V}_{O}}{{V}_{P}}=\frac{{V}_{N}}{{V}_{M}}.[/latex]
Подставляя это в уравнение для [латекса]{Q}_{\text{c}}\text{/}{Q}_{\text{h}},[/latex], мы получаем
[латекс]\frac{{Q}_{\text{c}}}{{Q}_{\text{h}}}=\frac{{T}_{\text{c}}}{{ Т} _ {\ текст {ч}}}. [/латекс]
Наконец, с помощью уравнения 4.2 мы находим, что КПД этого двигателя Карно на идеальном газе равен
[латекс] e = 1- \ frac {{T} _ {\ text {c}}} {{T} _ {\ text {h}}}. [/latex]
Двигатель не обязательно должен следовать циклу двигателя Карно. Все двигатели, однако, имеют один и тот же чистый эффект , а именно поглощение тепла из горячего резервуара, производство работы и отвод тепла в холодный резервуар. Это заставляет нас задаться вопросом: имеют ли все обратимые циклы, работающие между одними и теми же двумя резервуарами, одинаковую эффективность? Ответ на этот вопрос дает второй закон термодинамики, который обсуждался ранее: Все реверсивные циклы двигателя имеют одинаковую эффективность . Кроме того, как и следовало ожидать, все реальные двигатели, работающие между двумя резервуарами, менее эффективны, чем реверсивные двигатели, работающие между теми же двумя резервуарами. Это также является следствием второго закона термодинамики, показанного ранее.
Кроме того, как и следовало ожидать, все реальные двигатели, работающие между двумя резервуарами, менее эффективны, чем реверсивные двигатели, работающие между теми же двумя резервуарами. Это также является следствием второго закона термодинамики, показанного ранее.
Цикл идеального газового холодильника Карно представлен диаграммой pV на рис. 4.13. Это двигатель Карно, работающий в обратном направлении. Холодильник извлекает тепло [латекс]{Q}_{\text{c}}[/latex] из резервуара с низкой температурой при [латексе]{T}_{\text{c}}[/latex], когда идеально газ изотермически расширяется. Затем газ адиабатически сжимается до тех пор, пока его температура не достигнет [латекс] {T} _ {\ text {h}}, [/ латекс], после чего изотермическое сжатие газа приводит к выделению тепла [латекс] {Q} _ {\ text {h}}[/latex] сбрасывается в высокотемпературный резервуар в [latex]{T}_{\text{h}}.[/latex] Наконец, цикл завершается адиабатическим расширением газа, в результате чего его температура падает до [латекс] {T} _ {\ text {c}}. [/latex]
[/latex]
Рисунок 4.13 Работа, совершаемая над газом за один цикл холодильника Карно, показана и представлена площадью, ограниченной петлей MPONM.
Работа, совершенная над идеальным газом, равна площади, ограниченной путем диаграммы pV . Из первого закона эта работа равна
.
[латекс] W = {Q} _ {\ text {h}} — {Q} _ {\ text {c}}. [/latex]
Анализ, аналогичный анализу двигателя Карно, дает
[латекс]\frac{{Q}_{\text{c}}}{{T}_{\text{c}}}=\frac{{Q}_{\text{h}}}{{ Т}_{\текст{ч}}}.[/латекс]
В сочетании с уравнением 4.3 это дает
[латекс] {K} _ {\ text {R}} = \ frac {{T} _ {\ text {c}}} {{T} _ {\ text {h}} — {T} _ {\ текст{c}}}[/латекс]
для коэффициента полезного действия идеального газового холодильника Карно. Точно так же мы можем вычислить коэффициент полезного действия теплового насоса Карно как
.
[латекс] {K} _ {\ text {P}} = \ frac {{Q} _ {\ text {h}}} {{Q} _ {\ text {h}} — {Q} _ {\ text{c}}}=\frac{{T}_{\text{h}}}{{T}_{\text{h}}-{T}_{\text{c}}}. [/ латекс]
[/ латекс]
Мы только что нашли уравнения, представляющие КПД двигателя Карно и коэффициент полезного действия холодильника Карно или теплового насоса Карно, предполагая, что в качестве рабочего тела в обоих устройствах используется идеальный газ. Однако эти уравнения являются более общими, чем следует из их выводов. Вскоре мы покажем, что они оба верны независимо от того, какое рабочее вещество.
Карно обобщил свое исследование двигателя Карно и цикла Карно в то, что теперь известно как Принцип Карно :
Принцип Карно
Никакой двигатель, работающий между двумя резервуарами при постоянных температурах, не может иметь больший КПД, чем реверсивный двигатель.
Этот принцип можно рассматривать как еще одно утверждение второго закона термодинамики, и можно показать, что он эквивалентен утверждению Кельвина и утверждению Клаузиуса.
Пример
Двигатель Карно
Двигатель Карно имеет КПД 0,60, а температура его холодного резервуара составляет 300 К. (a) Какова температура горячего резервуара? б) Если двигатель совершает работу 300 Дж за цикл, сколько теплоты отводится из высокотемпературного резервуара за цикл? в) Сколько тепла отводится в низкотемпературный резервуар за цикл?
(a) Какова температура горячего резервуара? б) Если двигатель совершает работу 300 Дж за цикл, сколько теплоты отводится из высокотемпературного резервуара за цикл? в) Сколько тепла отводится в низкотемпературный резервуар за цикл?
Стратегия
Из температурной зависимости теплового КПД двигателя Карно можно найти температуру горячего резервуара. Тогда из определения КПД мы можем найти отводимое тепло при заданной работе, совершаемой двигателем. Наконец, экономия энергии приведет к тому, сколько тепла должно быть сброшено в холодный резервуар.
Решение
- Из [латекс]e=1-{T}_{\text{c}}\text{/}{T}_{\text{h}}[/latex] имеем
[латекс] 0,60 = 1- \ frac {300 \ phantom {\ rule {0.2em} {0ex}} \ text {K}} {{T} _ {\ text {h}}}, [/latex]
так, чтобы температура горячего резервуара была
[латекс]{T}_{\text{h}}=\frac{300\phantom{\rule{0.2em}{0ex}}\text{ K}}{1-0,60}=750\phantom{\rule{0.2em}{0ex}}\text{K}. [/latex]
[/latex]
- По определению КПД двигателя равен [latex]e= W\text{/}Q[/latex], так что теплота, отводимая от высокотемпературного резервуара за цикл, равна
[латекс] {Q} _ {\ text {h}} = \ frac {W} {e} = \ frac {300 \ phantom {\ rule {0.2em} {0ex}} \ text {J}} { 0,60}=500\phantom{\rule{0.2em}{0ex}}\text{J}.[/latex]
- Из первого закона теплота, отводимая двигателем в низкотемпературный резервуар за цикл, равна
[латекс] {Q} _ {\ text {c}} = {Q} _ {\ text {h}} -W = 500 \ phantom {\ rule {0.2em} {0ex}} \ text {J} -300\phantom{\rule{0.2em}{0ex}}\text{J}=200\phantom{\rule{0.2em}{0ex}}\text{J}.[/latex]
Значение
Двигатель Карно имеет максимально возможную эффективность преобразования тепла в работу между двумя резервуарами, но это не обязательно означает, что он [latex]100\text{%}[/latex] эффективен. По мере увеличения разницы температур горячего и холодного резервуара КПД двигателя Карно увеличивается.
Пример
Тепловой насос Карно
Представьте, что тепловой насос Карно работает при температуре наружного воздуха [латекс]0\phantom{\rule{0. 2em}{0ex}}\text{°C}[/latex] и внутренняя температура [латекс] 20,0 \ фантом {\ правило {0.2em} {0ex}} \ текст {°C} [/латекс]. Какую работу нужно совершить, если теплота, переданная внутрь дома, равна 30,0 кДж?
2em}{0ex}}\text{°C}[/latex] и внутренняя температура [латекс] 20,0 \ фантом {\ правило {0.2em} {0ex}} \ текст {°C} [/латекс]. Какую работу нужно совершить, если теплота, переданная внутрь дома, равна 30,0 кДж?
Стратегия
Поскольку предполагается, что тепловой насос является насосом Карно, его коэффициент производительности определяется как [латекс] {K} _ {\ text {P}} = {Q} _ {\ text {h}} \ text{/}W={T}_{\text{h}}\text{/}\left({T}_{\text{h}}-{T}_{\text{c}}\right ).[/latex] Таким образом, мы можем найти работу Вт от подведенного тепла [латекс]{Q}_{\text{h}}.[/латекс]
Решение
Необходимая работа получается из
[латекс]W={Q}_{\text{h}}\text{/}{K}_{\text{P}}={Q}_{\text{h}}\left({ T} _ {\ text {h}} — {T} _ {\ text {c}} \ right) \ text{/} {T} _ {\ text {h}} = 30 \ phantom {\ rule {0,2 em}{0ex}}\text{кДж}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\left(293\phantom{\rule{0.2em}{0ex}}\text{K}-273\phantom{\rule{0.2em}{0ex}}\text{K}\right)\text{/}293\phantom {\rule{0. 2em}{0ex}}\text{K}=2\phantom{\rule{0.2em}{0ex}}\text{kJ}.[/latex]
2em}{0ex}}\text{K}=2\phantom{\rule{0.2em}{0ex}}\text{kJ}.[/latex]
Значение
Отметим, что это работа зависит не только от тепла, подаваемого в дом, но и от температуры снаружи и внутри. Зависимость от температуры на улице делает нецелесообразным их использование в помещениях, где температура на улице значительно ниже комнатной.
С точки зрения затрат на электроэнергию тепловой насос является очень экономичным средством для обогрева зданий (рис. 4.14). Сравните этот метод с преобразованием электрической энергии непосредственно в тепло с помощью резистивных нагревательных элементов. В этом случае одна единица электрической энергии дает не более одной единицы тепла. К сожалению, у тепловых насосов есть проблемы, ограничивающие их полезность. Их покупка довольно дорогая по сравнению с резистивными нагревательными элементами, и, как показывает коэффициент полезного действия теплового насоса Карно, они становятся менее эффективными при понижении температуры наружного воздуха. На самом деле, ниже [латекс]–10\фантом{\правило{0,2em}{0ex}}\текст{°C}[/латекс], выделяемое ими тепло меньше, чем энергия, используемая для их работы.
На самом деле, ниже [латекс]–10\фантом{\правило{0,2em}{0ex}}\текст{°C}[/латекс], выделяемое ими тепло меньше, чем энергия, используемая для их работы.
Рисунок 4.14 Фотография теплового насоса (большая коробка), расположенного снаружи дома. Этот тепловой насос расположен в районе с теплым климатом, например на юге Соединенных Штатов, поскольку он был бы слишком неэффективным в северной части Соединенных Штатов. (кредит: модификация работы Питера Стивенса)
Проверьте свое понимание
Двигатель Карно работает между резервуарами при температуре [латекс]400\phantom{\rule{0.2em}{0ex}}\text{°C}[/latex] и [латекс]30\phantom{\rule {0.2em}{0ex}}\text{°C}[/latex]. а) Каков КПД двигателя? б) Если двигатель совершает работу 5,0 Дж за цикл, сколько теплоты за цикл он поглощает из высокотемпературного резервуара? в) Какое количество теплоты за цикл отводится в резервуар с низкой температурой? г) Какие температуры в холодном резервуаре дадут минимальный и максимальный КПД?
Показать раствор
а. [латекс]e=1-{T}_{\text{c}}\text{/}{T}_{\text{h}}=0,55[/латекс]; б. [латекс] {Q} _ {\ текст {h}} = eW = 9,1 \ фантом {\ правило {0.2em} {0ex}} \ текст {J} [/латекс]; в. [латекс] {Q} _ {\ text {c}} = {Q} _ {\ text {h}} -W = 4.1 \ phantom {\ rule {0.2em} {0ex}} \ text {J} [/ латекс]; д. [латекс] -273\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] и [латекс]400\phantom{\rule{0.2em}{0ex}} \text{°}\text{C}[/латекс]
[латекс]e=1-{T}_{\text{c}}\text{/}{T}_{\text{h}}=0,55[/латекс]; б. [латекс] {Q} _ {\ текст {h}} = eW = 9,1 \ фантом {\ правило {0.2em} {0ex}} \ текст {J} [/латекс]; в. [латекс] {Q} _ {\ text {c}} = {Q} _ {\ text {h}} -W = 4.1 \ phantom {\ rule {0.2em} {0ex}} \ text {J} [/ латекс]; д. [латекс] -273\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex] и [латекс]400\phantom{\rule{0.2em}{0ex}} \text{°}\text{C}[/латекс]
Проверьте свое понимание
Холодильник Карно работает между двумя тепловыми резервуарами, температура которых равна [латекс]0\фантом{\правило{0.2em}{0ex}}\текст{°}\текст{C}[/латекс] и [ латекс] 25 \ фантом {\ правило {0.2em} {0ex}} \ текст {°} \ текст {C} [/латекс]. а) Чему равен КПД холодильника? б) Если за цикл над рабочим телом совершается работа 200 Дж, то какое количество теплоты за цикл отбирается из холодного резервуара? в) Какое количество теплоты за цикл отдается горячему резервуару?
Показать раствор
а. [латекс] {K} _ {\ text {R}} = {T} _ {\ text {c}} \ text{/} \ left ({T} _ {\ text {h}} — {T} _ {\text{c}}\right)=10,9[/латекс]; б. [латекс] {Q} _ {\ текст {c}} = {K} _ {\ текст {R}} W = 2,18 \ фантом {\ правило {0.2em} {0ex}} \ текст {кДж} [/латекс ]; в. [латекс] {Q} _ {\ text {h}} = {Q} _ {\ text {c}} + W = 2,38 \ phantom {\ rule {0.2em} {0ex}} \ text {кДж} [/ латекс]
[латекс] {Q} _ {\ текст {c}} = {K} _ {\ текст {R}} W = 2,18 \ фантом {\ правило {0.2em} {0ex}} \ текст {кДж} [/латекс ]; в. [латекс] {Q} _ {\ text {h}} = {Q} _ {\ text {c}} + W = 2,38 \ phantom {\ rule {0.2em} {0ex}} \ text {кДж} [/ латекс]
Резюме
- Цикл Карно является наиболее эффективным двигателем для обратимого цикла, разработанного между двумя резервуарами.
- Принцип Карно — это еще один способ сформулировать второй закон термодинамики.
Концептуальные вопросы
Чтобы повысить эффективность двигателя Карно, следует ли повысить или понизить температуру горячего резервуара? А холодный резервуар?
Показать решение
Для повышения эффективности температура горячего резервуара должна быть повышена, а холодного резервуара – максимально снижена. Это видно из уравнения 4.3.
Как можно разработать двигатель Карно с эффективностью [latex]100\text{%}[/latex]?
Какие процессы происходят в цикле Карно?
Show Solution
адиабатические и изотермические процессы
Задачи
Температура холодного и горячего резервуаров, между которыми работает холодильник Карно, составляет [латекс]-73\фантом{\правило{0. 2em}{0ex}}\text{°}\text{C}[/latex ] и [латекс]270\фантом{\правило{0.2em}{0ex}}\текст{°C}[/латекс] соответственно. Каков его коэффициент полезного действия?
2em}{0ex}}\text{°}\text{C}[/latex ] и [латекс]270\фантом{\правило{0.2em}{0ex}}\текст{°C}[/латекс] соответственно. Каков его коэффициент полезного действия?
Показать решение
2.0
Предположим, что холодильник Карно работает между [латекс]{T}_{\text{c}}\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex }}{T}_{\text{h}}.[/latex] Рассчитайте количество работы, необходимой для извлечения 1,0 Дж тепла из холодного резервуара, если (a) [латекс]{T}_{\text{c }} = 7 \ фантом {\ правило {0.2em} {0ex}} \ текст {°} \ текст {C} [/латекс], [латекс] {T} _ {\ текст {ч}} = 27 \ фантом {\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]; (b) [латекс] {T} _ {\ text {c}} = -73 \ phantom {\ rule {0.2em} {0ex}} \ text {°} \ text {C} [/latex], [латекс ]{T}_{\text{h}}=27\phantom{\rule{0.2em}{0ex}}\text{°}\text{C;}[/latex] (c) [латекс]{T }_{\text{c}}=-173\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex], [латекс]{T}_{\text {h}}=27\phantom{\rule{0.2em}{0ex}}\text{°}\text{C}[/latex]; и (d) [латекс] {T} _ {\ text {c}} = -273 \ phantom {\ rule {0. 2em} {0ex}} \ text {°} \ text {C} [/latex], [ латекс] {T} _ {\ текст {h}} = 27 \ фантом {\ правило {0.2em} {0ex}} \ текст {°} \ текст {C} [/латекс].
2em} {0ex}} \ text {°} \ text {C} [/latex], [ латекс] {T} _ {\ текст {h}} = 27 \ фантом {\ правило {0.2em} {0ex}} \ текст {°} \ текст {C} [/латекс].
Двигатель Карно работает между резервуарами при температуре 600 и 300 К. Если двигатель поглощает 100 Дж за цикл в горячем резервуаре, какова его работа за цикл?
Демонстрационный раствор
50 Дж
Двигатель мощностью 500 Вт приводит в действие холодильник Карно между [латекс]-5\фантом{\правило{0.2em}{0ex}}\текст{°}\текст{C}[/латекс] и [латекс]30\фантом {\rule{0.2em}{0ex}}\text{°C}[/latex]. а) Какое количество тепла в секунду извлекается из холодильника? б) Какое количество теплоты отдается наружному воздуху в секунду?
Нарисуйте цикл Карно на диаграмме объем-температура.
Показать раствор
Тепловой насос Карно работает между [латекс]0\фантом{\правило{0.2em}{0ex}}\text{°C}[/латекс] и [латекс]20\фантом{\правило{0.2em}{0ex }}\text{°C}[/латекс]. Какое количество теплоты уходит внутрь дома на каждые 1,0 Дж работы, совершаемой насосом?
Двигатель, работающий между тепловыми резервуарами в точках [латекс]20\phantom{\rule{0. 2em}{0ex}}\text{°}\text{C}[/latex] и [латекс]200\phantom{\rule {0.2em}{0ex}}\text{°}\text{C}[/latex] извлекает 1000 Дж за цикл из горячего резервуара. а) Какую максимальную работу может совершить двигатель за цикл? б) Какое количество теплоты отводится в холодный резервуар при выполнении этой максимальной работы за один цикл?
2em}{0ex}}\text{°}\text{C}[/latex] и [латекс]200\phantom{\rule {0.2em}{0ex}}\text{°}\text{C}[/latex] извлекает 1000 Дж за цикл из горячего резервуара. а) Какую максимальную работу может совершить двигатель за цикл? б) Какое количество теплоты отводится в холодный резервуар при выполнении этой максимальной работы за один цикл?
Показать раствор
а. 381 Дж; б. 619 Дж
Предположим, что двигатель Карно может работать между двумя резервуарами либо как тепловой двигатель, либо как холодильник. Как связан КПД холодильника с КПД тепловой машины?
Двигатель Карно используется для измерения температуры теплового резервуара. Двигатель работает между резервуаром тепла и резервуаром, состоящим из воды в его тройной точке. (a) Если 400 Дж за цикл удаляется из теплового резервуара, а 200 Дж за цикл накапливается в тройном резервуаре, какова температура теплового резервуара? (b) Если 400 Дж за цикл удаляется из резервуара с тройной точкой, а 200 Дж за цикл накапливается в тепловом резервуаре, какова будет температура теплового резервуара?
Показать раствор
а.
 При этом может выделяться большое количество теплоты.
При этом может выделяться большое количество теплоты.


 Компрессор сжимает молекулы
Компрессор сжимает молекулы Цикл повторяется.
Цикл повторяется.
 {\gamma}=\phantom{\rule{0.2em}{0ex}}\text{constant}[/latex] и уравнения состояния для идеальный газ, [латекс]pV=nRT[/латекс], имеем 9{\gamma-1}.[/латекс]
{\gamma}=\phantom{\rule{0.2em}{0ex}}\text{constant}[/latex] и уравнения состояния для идеальный газ, [латекс]pV=nRT[/латекс], имеем 9{\gamma-1}.[/латекс] 2em}{0ex}}{T}_{\text{h}}[/latex] в данном конкретном случае. Обоснование шага 2 теперь дает 9{\gamma-1}.[/латекс]
2em}{0ex}}{T}_{\text{h}}[/latex] в данном конкретном случае. Обоснование шага 2 теперь дает 9{\gamma-1}.[/латекс]