Содержание
Электродвигатель постоянного тока
- Постоянная момента
- Постоянная ЭДС
- Постоянная электродвигателя
- Жесткость механической характеристики
- Напряжение электродвигателя
- Мощность электродвигателя постоянного тока
- Механическая постоянная времени
Постоянная момента
,
- где M — момент электродвигателя, Нм,
- – постоянная момента, Н∙м/А,
- I — сила тока, А
Постоянная ЭДС
Направление ЭДС определяется по правилу правой руки. Направление наводимой ЭДС противоположно направлению протекающего в проводнике тока.
Наведенная ЭДС последовательно изменяется по направлению из-за перемещения проводников в магнитном поле. Суммарная ЭДС, равная сумме ЭДС в каждой катушке, прикладывается к внешним выводам двигателя. Это и есть противо-ЭДС. Направление противо-ЭДС противоположно приложенному к двигателю напряжению. Значение противо-ЭДС пропорционально частоте вращения и определяется из следующего выражения: [1]
Направление противо-ЭДС противоположно приложенному к двигателю напряжению. Значение противо-ЭДС пропорционально частоте вращения и определяется из следующего выражения: [1]
,
- где — электродвижущая сила, В,
- – постоянная ЭДС, В∙с/рад,
- — угловая частота, рад/с
Постоянные момента и ЭДС в точности равны между собой KT = KE. Постоянные KT и KE равны друг другу, если они определены в единой системе едениц.
Постоянная электродвигателя
Одним из основных параметров электродвигателя постоянного тока является постоянная электродвигателя Kм. Постоянная электродвигателя определяет способность электродвигателя преобразовывать электрическую энергию в механическую.
,
- где — постоянная электродвигателя, Нм/√Вт,
- R — сопротивление обмоток, Ом,
- – максимальный момент, Нм,
- — мощность потребляемая при максимальном моменте, Вт
Справка: Постоянная электродвигателя вместе с размерами электродвигателя являются основными параметрами для инженера при выборе электродвигателя с лучшим соотношением мощность / объем.
Постоянная электродвигателя не зависит от соединения обмоток, при условии, что используется один и тот же материал проводника. Например, обмотка двигателя с 6 ветками и 2 параллельными проводами вместо 12 одиночных проводов удвоят постоянную ЭДС, при этом постоянная электродвигателя останется не изменой.
Жесткость механической характеристики двигателя
,
- где — жесткость механической характеристики электродвигателя постоянного тока
Напряжение электродвигателя
Уравнение баланса напряжений на зажимах двигателя постоянного тока имеет вид (в случае коллекторного двигателя не учитывается падение напряжения в щеточно-коллекторном узле):
,
- где U — напряжение, В.
Уравнение напряжения выраженное через момент двигателя будет выглядеть следующим образом:
Соотношение между моментом и частотой вращения при двух различных напряжениях питания двигателя постоянного тока неизменно. При увеличении частоты вращения момент линейно уменьшается. Наклон этой функции KTKE/R постоянный и не зависит от значения напряжения питания и частоты вращения двигателя.
Наклон этой функции KTKE/R постоянный и не зависит от значения напряжения питания и частоты вращения двигателя.
Благодаря таким характеристикам упрощается управление частотой вращения и углом поворота двигателей постоянного тока. Это характерно для коллекторных и вентильных двигателей постоянного тока, что нельзя сказать о двигателях переменного тока и шаговых двигателях [1].
Мощность электродвигателя постоянного тока
Упрощенная модель электродвигателя выглядит следующим образом:
- где I – сила тока, А
- U — напряжение, В,
- M — момент электродвигателя, Н∙м
- R — сопротивление токопроводящих элементов, Ом,
- L — индуктивность, Гн,
- Pэл — электрическая мощность (подведенная), Вт
- Pмех — механическая мощность (полезная), Вт
- Pтеп — тепловые потери, Вт
- Pинд — мощность затрачиваемая на заряд катушки индуктивности, Вт
- Pтр — потери на трение, Вт
Механическая постоянная времени
Механическая постоянная времени — это время, отсчитываемое с момента подачи постоянного напряжения на электродвигатель, за которое частота вращения ненагруженного электродвигателя достигает уровня в 63,21% (1-1/e) от своего конечного значения.
,
- где — механическая постоянная времени, с
Смотрите также
Основные параметры электродвигателя
Общие параметры для всех электродвигателей
- Момент электродвигателя
- Мощность электродвигателя
- Коэффициент полезного действия
- Номинальная частота вращения
- Момент инерции ротора
- Номинальное напряжение
- Электрическая постоянная времени
- Т.Кенио, С.Нагамори. Двигатели постоянного тока с постоянными магнитами: Пер. с англ.-М.: Энергоатомиздат, 1989.
Библиографический список
Динамические свойства асинхронных исполнительных двигателей (Лекция 18)
§ 1.4. Динамические свойства асинхронных исполнительных двигателей
Одним из главных
требований, предъявляемых к исполнительным двигателям, является требование
высокого быстродействия,под которым понимают способность двигателя
достигать заданной частоты вращения за максимально короткое время.
Быстродействие
определяется скоростью протекания электромагнитных и электромеханических
переходных процессов, возникающих в двигателе при подаче сигнала управления.
Как известно, скорость
затухания переходных процессов зависит от постоянных времени -
электромагнитной и электромеханической. Благодаря большому активному
сопротивлению ротора, электромагнитная постоянная времени Тэм=
L/r становится на порядок меньше электромеханической. Поэтому электромагнитными
переходными процессами здесь можно пренебречь и считать, что быстродействие
исполнительного двигателя определяется только электромеханической постоянной
времени. Последнюю найдем из уравнения движения при пуске двигателя вхолостую M
= J×dw/dt. Здесь J — момент инерции вращающихся
частей.
Механические характеристики идеального асинхронного исполнительного двигателя линейные, что
позволяет описать их одной формулой М = Мп(1 — w/wо), где wо и Мп -
угловая скорость холостого хода и пусковой момент. Подставив эту формулу в
Подставив эту формулу в
уравнение движения и решив его относительно w,
получим
где Тм — электромеханическая
постоянная, времени
(1.11)
На рис. 1.13 показана
кривая разгона двигателя, из которой видно, что угловая скорость вращения
асимптотически приближается к установившемуся значению wо. При t = Tмугловая
скорость вращения w = wо(1 — е-1) =
0,633wо. Следовательно,
постоянную Тм можно рассматривать как время разгона двигателя до
скорости, соответствующей 0,633wо.
Рис. 1.13. Кривая разгона двигателя при пуске в холостую
При амплитудном
управлении
механические характеристики непараллельные, т.е. пусковой момент
пропорционален коэффициенту сигнала Мп = Мпкaэ, где Мпк -
пусковой
момент при круговом поле, а угловая скорость
идеального холостого хода — не пропорциональна aэ. Ее значение найдем из
Ее значение найдем из
(1.6), положив m
= 0
Подставим эти значения Мп
и wо в (1.11), получим
Из этой формулы видно, что с уменьшением коэффициента сигнала, электромеханическая
постоянная времени растет, а это значит — быстродействие исполнительного двигателя
ухудшается. Сказанное относится и к конденсаторному управлению, чьи
характеристики похожи на характеристики при амплитудном управлении.
При фазовом управлении механические
характеристики параллельные, т.е. пусковой момент и угловая скорость холостого
хода изменяются пропорционально коэффициенту сигнала (Мп = Мпкsinb, wо = w1sinb) . В этом случае электромеханическая
постоянная времени будет
т.е. при фазовом управлении постоянная времени и
быстродействие не зависят от коэффициента сигнала.
Так как механические характеристики реальных двигателей проходят выше идеальных, постоянные
времени реальных двигателей всегда получаются немного меньше идеальных.
Однако сказанное выше относительно влияния коэффициента сигнала на
быстродействие остается справедливым и здесь.
В выражения постоянных времени входит значение угловой скорости вращения wо = 2pf/p, следовательно, на
величину Тмвлияет частота сети и число пар полюсов машины.
По этой причине двигатели, рассчитанные на повышенную частоту, имеют большую
постоянную времени и худшее быстродействие, чем двигатели, спроектированные на
частоту 50 Гц (см. табл.1).
Таблица1. Электромеханические постоянные
времени асинхронных исполнительных двигателей
|
Тип двигателя | Тм,
| |
50 Гц | 400 Гц | |
АИД с полым немагнитным ротором | 0,005 ¸ 0,05 |
0,015 ¸ 0,10 |
|
АИД с полым ферромагнитным ротором
| 0,200 ¸ 1,00
|
0,300 ¸ 3,00
|
|
АИД с ротором «беличья клетка»
|
0,020 ¸ 0,10
| 0,050 ¸ 0,15
|
§ 1.
 5. Самоход и пути его устранения
5. Самоход и пути его устранения
Самоходом называется
вращение двигателя при отсутствии сигнала управления. На практике различают
два вида самохода: 1) технологический и 2) параметрический.
Технологический самоход проявляется в начале вращения двигателя при подаче только
напряжения возбуждения.
Причинами технологического самохода являются слабые эллиптические поля, возникающие в двигателе,
благодаря наличию короткозамкнутых контуров в сердечниках и обмотках из-за
их плохой изоляции, благодаря неравномерности воздушного зазора,
неодинаковой магнитной проводимости стали вдоль и поперек проката и другим
факторам технологического характера, приводящим к разделению магнитного
потока возбуждения на два, сдвинутых в пространстве и во времени. Как
известно, этого достаточно для возникновения вращающихся полей (см. асинхронный
двигатель с экранированными полюсами).
Для устранения
технологического самохода необходима тщательная технологическая проработка
двигателя и высокая культура его производства: хорошая изоляция обмотки и
листов стали, точная механическая обработка деталей, обязательна вееробразная
шихтовка пакетов — смещение каждого последующего листа на одно зубцовое
деление относительно предыдущего.
Параметрический самоход проявляется в продолжении вращения двигателя после снятия
сигнала управления.
При снятии сигнала управления исполнительный двигатель становится однофазным, который хотя и не
имеет собственного пускового момента, но, будучи раскрученным, продолжает
работать. Для исполнительного двигателя такое явление не допустимо.
С целью устранения
параметрического самохода асинхронные исполнительные двигатели
изготавливаются с роторами, имеющими большое активное сопротивление. В
результате момент однофазной машины становится не движущим (+) а тормозящим (-),
в чем легко убедиться, рассматривая характеристики двух однофазных двигателей с
различными критическими скольжениями: sк = 0,3 и sк = 1
(рис. 1.14,а и б).
Рис. 1.14. Механические характеристики однофазного двигателя с sk = 0,3 (а) и
sk = 1 (б)
Таким образом, критические скольжения асинхронных исполнительных двигателей должны быть
равными или большими единицы. В реальных двигателях sк= 2¸3, а отдельных случаях
В реальных двигателях sк= 2¸3, а отдельных случаях
даже sк = 7¸8.
Критерий (условие)
отсутствия самохода найдем на основании схемы замещения однофазного
асинхронного двигателя (рис. 1.15)
В отличии от известной
схемы [1], здесь отсутствуют индуктивные сопротивления ротора, которыми мы
пренебрегли ввиду их малости по сравнению с активными сопротивлениями rр.
Рис. 1.15. Схема замещения однофазного асинхронного двигателя
Преобразуем эту схему, заменив параллельные контуры последовательными (рис.1.16)
Рис. 1.16. Преобразованная схема замещения однофазного асинхронного
двигателя
Электромагнитная мощность однофазного двигателя с точки зрения превращения ее в полезную
механическую мощность равна разности электромагнитных мощностей прямой и
обратной последовательностей
Самоход будет отсутствовать, если электромагнитная мощность машины будет равна нулю или даже
отрицательной, т. е. Рэм <0. Это приводит к
е. Рэм <0. Это приводит к
условию
(1.12)
Полные сопротивления вторичного контура преобразованных схем замещения
Их активные составляющие соответственно
Подставляя значения R21
и R22 в (1.12), получим
Если учесть, что для режима электромагнитного тормоза начальное скольжение s = 1, окончательно
Таким образом, для устранения самохода исполнительный двигатель должен иметь
активное сопротивление ротора, приведенное к статору, большим или равным
реактивному сопротивлению взаимной индуктивности.
При этом еще раз следует
напомнить, что большое активное сопротивление ротора приводит к значительным
потерям в обмотках, снижению КПД и ухудшению использования машины.
§ 1.6. Конструкции асинхронных исполнительных двигателей
Асинхронные
исполнительные двигатели выпускаются следующих видов:
1) с полым немагнитным ротором; 2) с полым
ферромагнитным ротором; 3) с короткозамкнутым ротором типа «беличья
клетка».
Асинхронные исполнительные двигатели с полым немагнитным ротором. Сегодня это, пожалуй,
самые распространенные асинхронные исполнительные двигатели. Они применяются
в различных системах автоматического управления и выпускаются целым рядом
заводов. Их мощности — от десятых долей ватта до сотен ватт. Они
рассчитываются на промышленную частоту (50 Гц) и на повышенные частоты (200,
400, 500 Гц). Угловые скорости вращения колеблются от 1500 до 30000 об/мин.
Одна из конструктивных
схем двигателя с полым немагнитным ротором представлена на рис. 1.17. Двигатель
состоит из внешнего статора 1 с обмотками возбуждения и управления;
внутреннего статора-сердечника 2 без обмоток, служащего лишь для уменьшения
магнитного сопротивления на пути главного потока; полого немагнитного ротора
3, выполненного из материала с высоким удельным сопротивлением (чаще всего из
сплавов алюминия). Толщина стенок ротора составляет 0,1-1 мм. Весьма
небольшая масса ротора делает его малоинерционным, что придает двигателю
очень ценные свойства. Между стенками ротора и обоими статорами выполняются
Между стенками ротора и обоими статорами выполняются
воздушные зазоры, величина которых обычно не превосходит 0,15-0,25 мм.
Однако, эти зазоры вместе c немагнитным ротором создают большие немагнитные
промежутки между внешним и внутренним статорами, что приводит к большим
намагничивающим токам, достигающим 90 % от номинального значения.
Рис. 1.17. Асинхронный исполнительный двигатель с полым немагнитным
ротором
Двигатели мощностью 0,1-5 Вт изготавливают несколько иначе. Поскольку такие двигатели имеют
малые внутренние диаметры, то для облегчения укладки обмоток их размещают в
пазах внутреннего статора, а внешний делают без обмоток. Правда, это
приводит к некоторому увеличению диаметра ротора, а следовательно и его момента
инерции. Для устранения последнего недостатка иногда используют третью
конструкцию: одну из обмоток размещают на внутреннем, а другую — на внешнем
статоре.
Достоинства двигателей с полым немагнитным ротором.
1) Малый момент инерции, что в совокупности со
значительным пусковым моментом обеспечивает высокое быстродействие.
Электромеханические постоянные времени большинства их них лежат в пределах:
0,01-0,1 с. при f = 50 Гц и 0,02-0,15 с. при f = 400 Гц.
2) Сравнительно хорошая линейность
механических и регулировочных характеристик, чему в известной мере
способствуют весьма незначительные индуктивные сопротивления немагнитного
ротора [xр = (0,05-0,1)rр].
3) Высокая чувствительность — малое напряжение
трогания, что объясняется малым моментом инерции и отсутствием односторонних
сил магнитного притяжения, поскольку ротор выполнен из немагнитного материала.
Недостатки двигателей с полым немагнитным ротором.
1) Низкие энергетические показатели, что
объясняется большими намагничивающими токами, приводящими к значительным
потерям в обмотках.
2) Большие габариты и масса, обусловленные
первым недостатком.
Асинхронные исполнительные двигатели с полым немагнитным ротором выпускаются сериями АДП,
ДИД, ЭМ. Как правило, первая серия предназначена для устройств наземной
автоматики, вторая — для авиационной и космической техники, а третья — для
средств вычислительной техники.
Асинхронные
исполнительные двигатели с полым ферромагнитным ротором. В отличии от двигателей
первого типа ротор этого двигателя выполняется из магнитного материала с
толщиной стенок 0,3-3 мм, поэтому здесь отсутствует внутренний статор. Воздушный
зазор небольшой (0,2-0,3 мм). Однако намагничивающий ток (Im) этого двигателя
практически мало отличается от Im двигателя с полым
немагнитным ротором, т.к.проводимость
ротора и здесь невысокая вследствие его малой толщины.
Двигатель имеет большой
момент инерции и небольшой пусковой момент, что значительно ухудшает его
быстродействие. Приемы, связанные сомеднением ротора с целью увеличения пускового
момента, оказались малоэффективными. Существенным недостатком являются большие силы
Существенным недостатком являются большие силы
одностороннего магнитного притяжения, приводящие порой к залипанию ротора и
отказам вработе. Вцелом эти двигатели
значительно уступают двигателям с полымнемагнитным ротором, поэтому они не получили
широкого распространения.
Асинхронные двигатели с
короткозамкнутым ротором выпускаются обычного исполнения и специальной, так
называемой «сквозной» конструкции.
Первые отличаются от
силовых машин только повышенным активным сопротивлением ротора и используются в
тех установках, где требования высокого быстродействия не играют существенной
роли. Вторые имеют оригинальную конструкцию, суть которой состоит в том, что
диаметр расточки статора Di равен наружному диаметру
подшипника Dп (рис. 1.18) Такая конструкция позволяет
проводить окончательную обработку (шлифовку) внутренней поверхности статора
и отверстий под подшипники в подшипниковых щитах за одну установку двигателя на
станке.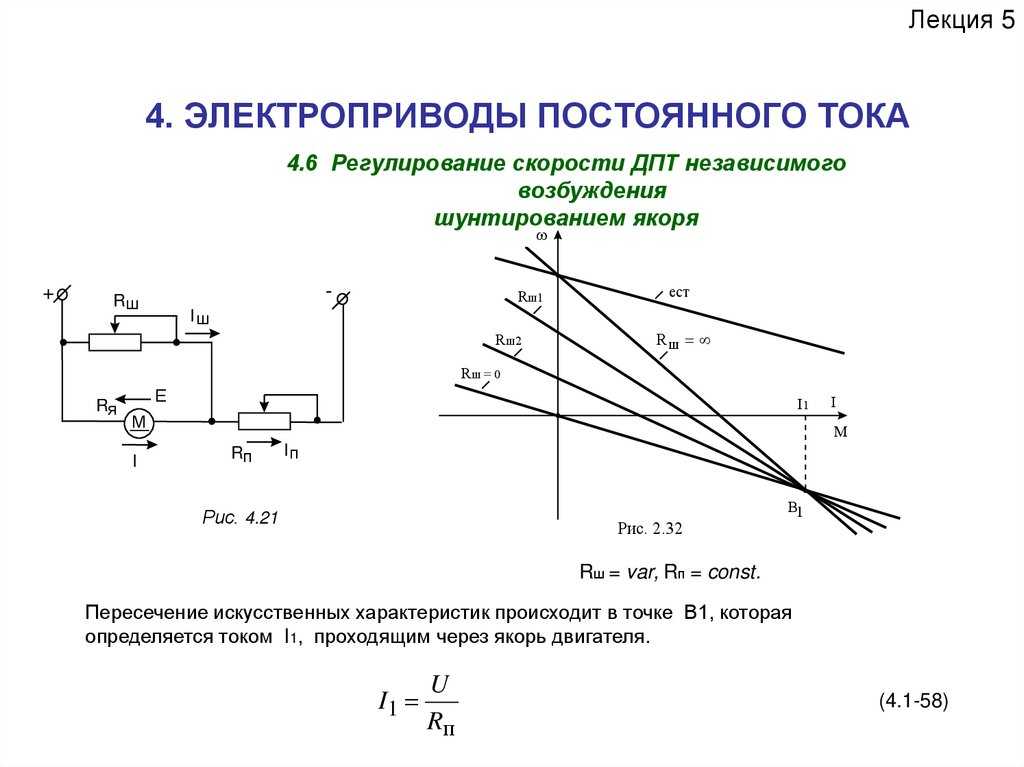 Конечно, перед этим подшипниковые щиты должны быть закреплены на
Конечно, перед этим подшипниковые щиты должны быть закреплены на
статоре. Обычно лобовые части покрывают специальным компаундом для
предохранения их от металлической стружки.
Рис. 1.18. Асинхронный исполнительный двигатель «сквозной»
конструкции
«Сквозная» конструкция позволяет получать воздушные зазоры в 0,03-0,05 мм, что на порядок
меньше, чем в двигателях традиционной конструкции. Кроме того, для уменьшения
момента инерции их выполняют с малым диаметром и увеличенной длиной ротора.
Обычно Lр/Dр = 2-3.
Малые воздушные зазоры
резко уменьшают намагничивающий ток, увеличивают КПД, cosj, вращающий момент
двигателя. Однако сравнительно большой момент инерции (по отношению к двигателям
с полым немагнитным ротором) приводит к увеличению электромеханической
постоянной времени.
Далее…
Константы пьезоэлектрического заряда
Поскольку пьезоэлектрическая керамика анизотропна, физические константы относятся как к направлению приложенной механической или электрической силы, так и к направлениям, перпендикулярным приложенной силе. Следовательно, каждая константа обычно имеет два нижних индекса, которые указывают направления двух связанных величин, таких как напряжение (сила, действующая на керамический элемент/площадь поверхности элемента) и деформация (изменение длины элемента/первоначальная длина элемента) для упругости. . Направление положительной поляризации обычно совпадает с осью Z прямоугольной системы осей X, Y и Z ( Рисунок 1.6 ). Направление X, Y или Z представлено нижними индексами 1, 2 или 3 соответственно, а сдвиг относительно одной из этих осей представлен нижними индексами 4, 5 или 6 соответственно. Здесь приведены определения наиболее часто используемых констант, а также уравнения для определения и взаимосвязи этих констант. Постоянная пьезоэлектрического заряда , d, постоянная пьезоэлектрического напряжения , g и диэлектрическая проницаемость , e являются факторами, зависящими от температуры.
Следовательно, каждая константа обычно имеет два нижних индекса, которые указывают направления двух связанных величин, таких как напряжение (сила, действующая на керамический элемент/площадь поверхности элемента) и деформация (изменение длины элемента/первоначальная длина элемента) для упругости. . Направление положительной поляризации обычно совпадает с осью Z прямоугольной системы осей X, Y и Z ( Рисунок 1.6 ). Направление X, Y или Z представлено нижними индексами 1, 2 или 3 соответственно, а сдвиг относительно одной из этих осей представлен нижними индексами 4, 5 или 6 соответственно. Здесь приведены определения наиболее часто используемых констант, а также уравнения для определения и взаимосвязи этих констант. Постоянная пьезоэлектрического заряда , d, постоянная пьезоэлектрического напряжения , g и диэлектрическая проницаемость , e являются факторами, зависящими от температуры.
Рисунок 1.6 – Направление положительной поляризации обычно совпадает с осью Z.
Константа пьезоэлектрического заряда
Постоянная пьезоэлектрического заряда , d, представляет собой поляризацию, создаваемую на единицу механического напряжения (T), приложенного к пьезоэлектрическому материалу, или, альтернативно, представляет собой механическое напряжение (S), испытываемое пьезоэлектрическим материалом на единицу приложенного электрического поля. Первый нижний индекс d указывает направление поляризации, создаваемой в материале, когда электрическое поле Е равно нулю, или, альтернативно, является направлением напряженности приложенного поля. Второй нижний индекс — это направление приложенного напряжения или индуцированной деформации соответственно. Поскольку деформация, вызываемая в пьезоэлектрическом материале приложенным электрическим полем, является произведением значения электрического поля и значения d, d является важным показателем пригодности материала для приложений, зависящих от деформации (привод).
| д 33 | индуцированная поляризация в направлении 3 (параллельно направлению, в котором поляризован керамический элемент) на единицу напряжения, приложенного в направлении 3 или индуцированная деформация в направлении 3 на единицу электрического поля, приложенного в направлении 3 |
| д 31 | индуцированная поляризация в направлении 3 (параллельно направлению поляризации керамического элемента) на единицу напряжения, приложенного в направлении 1 (перпендикулярно направлению поляризации керамического элемента) или индуцированная деформация в направлении 1 на единицу электрического поля, приложенного в направлении 3 |
| д 15 | индуцированная поляризация в направлении 1 (перпендикулярно направлению поляризации керамического элемента) на единицу напряжения сдвига, приложенного относительно направления 2 (направление 2 перпендикулярно направлению, в котором поляризован керамический элемент) или индуцированная деформация сдвига относительно направления 2 на единица электрического поля, приложенная в направлении 1 |
Пьезоэлектрическая постоянная напряжения
Постоянная пьезоэлектрического напряжения , г, представляет собой электрическое поле, создаваемое пьезоэлектрическим материалом на единицу приложенного механического напряжения, или, альтернативно, представляет собой механическое напряжение, испытываемое пьезоэлектрическим материалом на единицу приложенного электрического смещения. Первый нижний индекс g указывает направление электрического поля, создаваемого в материале, или направление приложенного электрического смещения. Второй нижний индекс — это направление приложенного напряжения или индуцированной деформации соответственно. Поскольку сила индуцированного электрического поля, создаваемого пьезоэлектрическим материалом в ответ на приложенное физическое напряжение, является произведением значения приложенного напряжения и значения g, g важно для оценки пригодности материала для сенсорных приложений. .
Первый нижний индекс g указывает направление электрического поля, создаваемого в материале, или направление приложенного электрического смещения. Второй нижний индекс — это направление приложенного напряжения или индуцированной деформации соответственно. Поскольку сила индуцированного электрического поля, создаваемого пьезоэлектрическим материалом в ответ на приложенное физическое напряжение, является произведением значения приложенного напряжения и значения g, g важно для оценки пригодности материала для сенсорных приложений. .
| г 33 | индуцированное электрическое поле в направлении 3 (параллельно направлению, в котором поляризован керамический элемент) на единицу напряжения, приложенного в направлении 3 или индуцированное напряжение в направлении 3 на единицу электрического смещения, приложенного в направлении 3 |
| г 31 | индуцируемое электрическое поле в направлении 3 (параллельно направлению поляризации керамического элемента) на единицу напряжения, приложенного в направлении 1 (перпендикулярно направлению поляризации керамического элемента) или Индуцированная деформация в направлении 1 на единицу электрического смещения, приложенного в направлении 3 |
| г 15 | индуцированное электрическое поле в направлении 1 (перпендикулярно направлению поляризации керамического элемента) на единицу напряжения сдвига, приложенное относительно направления 2 (направление 2 перпендикулярно направлению, в котором поляризован керамический элемент) или индуцированная деформация сдвига относительно направления 2 на единицу электрического смещения, приложенного в направлении 1 |
Постоянная диэлектрической проницаемости
Диэлектрическая проницаемость , или диэлектрическая проницаемость , ε, для пьезоэлектрического керамического материала представляет собой диэлектрическое смещение на единицу электрического поля. ε T — диэлектрическая проницаемость при постоянном напряжении, ε S — диэлектрическая проницаемость при постоянной деформации. Первый нижний индекс ε> указывает направление диэлектрического смещения; второй — направление электрического поля.
ε T — диэлектрическая проницаемость при постоянном напряжении, ε S — диэлектрическая проницаемость при постоянной деформации. Первый нижний индекс ε> указывает направление диэлектрического смещения; второй — направление электрического поля.
Относительная диэлектрическая проницаемость, К, представляет собой отношение количества заряда, которое элемент, изготовленный из керамического материала, может накапливать, к абсолютной диэлектрической проницаемости, 0, заряду, который может храниться теми же электродами, когда они разделены вакуум, при равном напряжении (0 = 8,85 х 10-12 фарад/метр).
| ε T 11 | диэлектрическая проницаемость диэлектрического смещения и электрического поля в направлении 1 (перпендикулярном направлению, в котором поляризован керамический элемент), при постоянном напряжении |
| ε S 33 | диэлектрическая проницаемость диэлектрического смещения и электрического поля в направлении 3 (параллельном направлению, в котором поляризован керамический элемент), при постоянной деформации |
Эластичность и соответствие
Упругая податливость , с, представляет собой деформацию, возникающую в пьезоэлектрическом материале на единицу приложенного напряжения, и для направлений 11 и 33 является обратной величиной модуля упругости (модуля Юнга, Y). с D – податливость при постоянном электрическом смещении; s E – податливость в постоянном электрическом поле. Первый нижний индекс указывает направление деформации, второй – направление напряжения.
с D – податливость при постоянном электрическом смещении; s E – податливость в постоянном электрическом поле. Первый нижний индекс указывает направление деформации, второй – направление напряжения.
| с Е 11 | эластичная податливость к напряжению в направлении 1 (перпендикулярно направлению полярности керамического элемента) и сопутствующей деформации в направлении 1 в постоянном электрическом поле (короткое замыкание) |
| с Д 33 | упругая податливость к напряжению в направлении 3 (параллельно направлению полярности керамического элемента) и сопутствующей деформации в направлении 3 при постоянном электрическом смещении (разомкнутая цепь) |
Модуль Юнга
Модуль Юнга , Y, является показателем жесткости (упругости) керамического материала. Y определяется путем деления значения напряжения, приложенного к материалу, на значение результирующей деформации в том же направлении.
Y определяется путем деления значения напряжения, приложенного к материалу, на значение результирующей деформации в том же направлении.
Коэффициент электромеханического сцепления
Коэффициент электромеханической связи , k, является показателем эффективности, с которой пьезоэлектрический материал преобразует электрическую энергию в механическую или преобразует механическую энергию в электрическую. Первый индекс к k обозначает направление, вдоль которого применяются электроды; второй обозначает направление, вдоль которого применяется или развивается механическая энергия.
Значения
k, указанные в спецификациях поставщиков керамики, обычно являются теоретическими максимальными значениями. При низких входных частотах типичная пьезоэлектрическая керамика может преобразовывать 30-75% энергии, поступающей к ней в одной форме, в другую форму, в зависимости от состава керамики и направления действующих сил.
Высокое значение k обычно желательно для эффективного преобразования энергии, но k не учитывает ни диэлектрические потери, ни механические потери, ни рекуперацию непреобразованной энергии. Точной мерой эффективности является отношение преобразованной полезной энергии, отдаваемой пьезоэлектрическим элементом, к общей энергии, потребляемой элементом. По этому показателю пьезоэлектрическая технология в хорошо спроектированных системах может демонстрировать КПД, превышающий 90%.
Точной мерой эффективности является отношение преобразованной полезной энергии, отдаваемой пьезоэлектрическим элементом, к общей энергии, потребляемой элементом. По этому показателю пьезоэлектрическая технология в хорошо спроектированных системах может демонстрировать КПД, превышающий 90%.
Размеры керамического элемента могут диктовать уникальные выражения k. Для тонкого диска из пьезоэлектрической керамики планарный коэффициент связи kp выражает радиальную связь — связь между электрическим полем, параллельным направлению поляризации керамического элемента (направление 3), и механическими воздействиями, вызывающими радиальные колебания относительно поверхности диска. направление поляризации (направление 1 и направление 2). Для диска или пластины из материала, размеры поверхности которого велики по сравнению с его толщиной, коэффициент связи толщины, kt, уникальное выражение k33, выражает связь между электрическим полем в направлении 3 и механическими вибрациями в том же направлении. Резонансная частота для толщины элемента такой формы намного выше, чем резонансная частота для поперечных размеров. В то же время сильно затухающие поперечные колебания на этой более высокой резонансной частоте в результате поперечного сжатия/расширения, сопровождающего расширение/сжатие по толщине, делают kt ниже k33, соответствующего коэффициента для продольных колебаний тонкого стержня тот же материал, для которого гораздо более низкая частота продольного резонанса более точно соответствует частоте поперечного резонанса.
Резонансная частота для толщины элемента такой формы намного выше, чем резонансная частота для поперечных размеров. В то же время сильно затухающие поперечные колебания на этой более высокой резонансной частоте в результате поперечного сжатия/расширения, сопровождающего расширение/сжатие по толщине, делают kt ниже k33, соответствующего коэффициента для продольных колебаний тонкого стержня тот же материал, для которого гораздо более низкая частота продольного резонанса более точно соответствует частоте поперечного резонанса.
| к 33 | коэффициент для электрического поля в направлении 3 (параллельно направлению, в котором поляризован керамический элемент) и продольных колебаний в направлении 3 (керамический стержень, длина >10 диаметров) |
| к т | коэффициент для электрического поля в направлении 3 и вибрации в направлении 3 (тонкий диск, размеры поверхности большие по сравнению с толщиной; k т < к 33 ) |
| к 31 | коэффициент для электрического поля в направлении 3 (параллельно направлению поляризации керамического элемента) и продольных колебаний в направлении 1 (перпендикулярно направлению поляризации керамического элемента) (керамический стержень) |
| к р | коэффициент для электрического поля в направлении 3 (параллельно направлению поляризации керамического элемента) и радиальных колебаний в направлениях 1 и 2 (оба направления перпендикулярны направлению поляризации керамического элемента) (тонкий диск) |
Коэффициент диэлектрических потерь
δ, tan δ, для керамического материала представляет собой тангенс угла диэлектрических потерь. tan δ определяется отношением эффективной проводимости к эффективной проводимости в параллельной цепи, измеренной с помощью импедансного моста. Значения тангенса δ обычно определяются на частоте 1 кГц.
tan δ определяется отношением эффективной проводимости к эффективной проводимости в параллельной цепи, измеренной с помощью импедансного моста. Значения тангенса δ обычно определяются на частоте 1 кГц.
Пьезоэлектрическая постоянная частоты
При воздействии на неограниченный пьезоэлектрический керамический элемент высокочастотного переменного электрического поля минимум импеданса, планарная или радиальная резонансная частота, совпадает с последовательной резонансной частотой, f с . Отношение между константой частоты резонанса радиальной моды , N P и диаметром керамического элемента, DΦ , выражается следующим образом: , встречается осевая резонансная частота . Постоянная частоты моды толщины, N T , связана с толщиной керамического элемента, h, соотношением:
N T = f с h
Третья постоянная частоты, постоянная частоты продольной моды , связана с длиной элемента:
N L = f с l
Наиболее часто используемые константы и уравнения
Скорость старения
Скорость старения = (Пар 2 — Пар 1 ) / ((Пар 1 ) (log t 2 — log t 1 ))
Полоса пропускания4 B 900≥40 или B ≡ kf с
Диэлектрическая проницаемость (относительная)
диэлектрическая проницаемость керамического материала / диэлектрическая проницаемость свободного пространства*
K T = ε T / <ε 0
*8,85 x 10-12 фарад/метр для параллельной схемы эквивалентно керамическому элементу;
тангенс угла потерь (тангенс d)
измерение непосредственно, как правило, на частоте 1 кГц
Упругое соответствие
развиваемая деформация/приложенное напряжение;
обратное значение модуля Юнга (упругости)
с = 1 / ν 2
с D 33 = 1 / Y D 33
с E 5 5 3 3 = E 33
с D 11 = 1 / Y D 11
s E 11 = 1 / Y E 11
Электромеханическая энергия
или
преобразованная электрическая энергия/ подводимая механическая энергия
Статические/низкие частоты
Керамическая пластина
k 31 2 = d 31 2 / (s E 11 3 Tε 035 )
керамический диск
k p 2 = 2d 31 2 / ((s E 11 + s E 12 )ε T 3 0 4)керамика стержень
k 33 2 = d 33 2 / (с Е 33 ε T 33 )
Более высокие частоты
керамическая пластина
керамический диск
k p ≅ √ [(2,51 (f
— 4 m 3 n 5) 5 / ф н ) — ( (f n — f m ) / f n ) 2 ]
керамический стержень
k 33 2 = (π / 3 м n 903 94 ) загар [(π / 2) ((f n — f m ) / f n )]
любая форма
k eff 2 = (f n 2 — f m 2 ) / f n 2
Частота Постоянная
резонансная частота 34 L (продольный режим) = f s l
N P (радиальная мода) = f s DΦ
N T (режим толщины) = f s h
Механическая добротность керамики
реактивное сопротивление / сопротивление для последовательной цепи элемент
Q м = f n 2 / (2πf м C 0 Z м (f n 5 м 2 139 2 ))
Константа пьезоэлектрического заряда
электрическое поле, создаваемое единицей площади керамики / приложенное напряжение
или
деформация керамического элемента / единица приложенного электрического поля
d = k√(s E ε T )
d 31 = k 31 √( с Е 11 ε Т 33 )
d 33 = k 33 √(s E 33 ε T 33 0 39035 33 0 39035 ) 9004 5 = k 15 E 55 ε T 11 )
Пьезоэлектрическая константа напряжения
генерируемое электрическое поле / приложенное напряжение
или
деформация керамического элемента / приложенное электрическое смещение
g = d / εT
g 31 = d 31 9013 9013 9013 9003 9013 33
г 33 = d 33 / ε T 33
г 15 = d 15 / ε T Young’s 5
приложенное напряжение / развиваемая деформация
Y = (F / A ) / (Δl / l) = T / S
Связь между d, ε T и g
g = d / ε T или d = gε T
Символы
| А | площадь поверхности керамического элемента (м 2 ) |
| Б | пропускная способность (частота) |
| д | Константа пьезоэлектрического заряда (C/N) |
| DΦ | диаметр керамического диска или стержня (м) |
| ε 0 | диэлектрическая проницаемость свободного пространства (8,85 х 10 -12 фарад/м) |
| е Т | диэлектрическая проницаемость керамического материала (фарад/м) (при постоянном напряжении |
| Ф | сила |
| е м | минимальная частота импеданса (резонансная частота) (Гц) |
| ж п | максимальная частота импеданса (антирезонансная частота) (Гц) |
| ф р | параллельная резонансная частота (Гц) |
| ж с | (Гц) |
| г | Константа пьезоэлектрического напряжения (Вм/Н) |
| ч | высота (толщина) керамического элемента (м) |
| к | коэффициент электромеханического сцепления |
| к эфф | эффективный коэффициент связи |
| К Т | относительная диэлектрическая проницаемость (при постоянном напряжении) |
| л | начальная длина керамического элемента (м) |
| Н | постоянная частоты (Гц * м) |
Пар. 1 1 | значение параметра Par при t 1 (дни) |
| Параметр 2 | значение параметра Par при t 2 (дни) |
| Q м | механическая добротность |
| р | плотность керамики (кг/м 3 ) |
| с | упругое соответствие (м 2 /Н) |
| С | штамм |
| т 1 | время 1 после поляризации (дни) |
| т 2 | время 2 после поляризации (дни) |
| тангенс δ | коэффициент диэлектрических потерь |
| Т | стресс |
| Т или | температура |
| Т С | Точка Кюри (°C) |
| ν> | скорость звука в керамическом материале (м/с) |
| с | ширина керамического элемента (м) |
| Д | Модуль Юнга (Н/м 2 ) |
| Z м | минимальное сопротивление при f м (Ом) |
Для получения более подробной информации о пьезокерамике и ее использовании закажите нашу книгу |
Есть вопросы о пьезоизделиях APC International? Свяжитесь с нами или позвоните по телефону (570) 726-6961, чтобы узнать больше информации.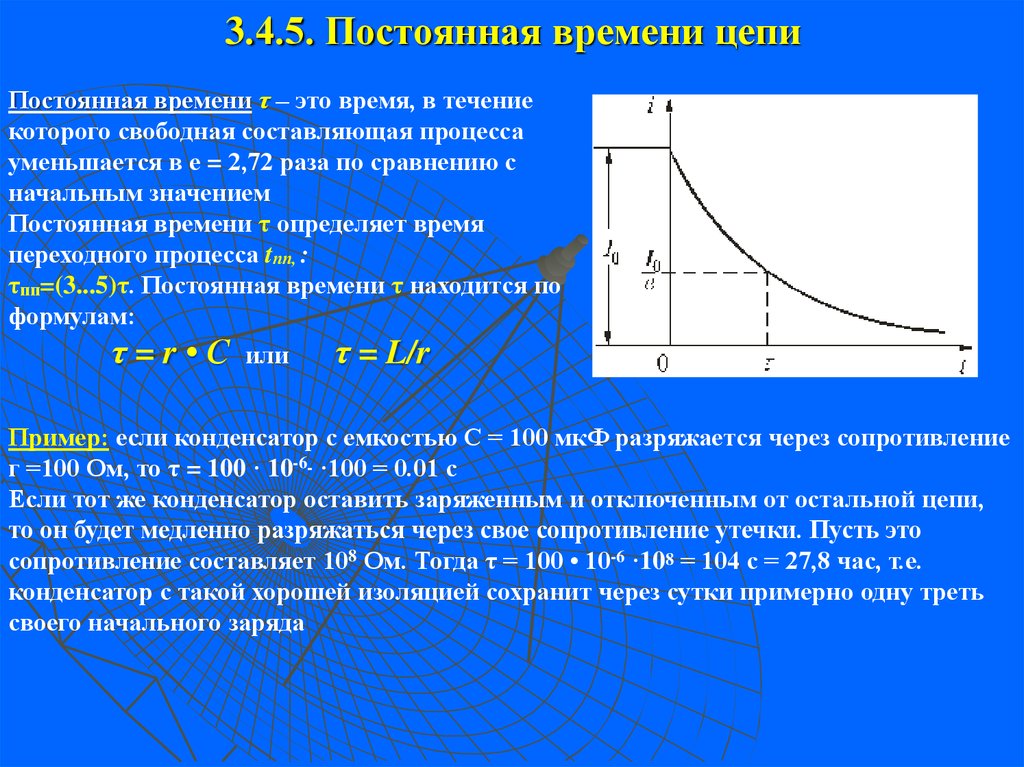
Интерфейс между электрическим и механическим вращающимся
домены
Перейти к содержимому
Основное содержание
Интерфейс между электрическим и механическим вращающимся
домены
Библиотека
Электрические элементы
Описание
Блок вращательного электромеханического преобразователя
обеспечивает интерфейс между электрическим и механическим вращательным
домены. Он преобразует электрическую энергию в механическую в
форму вращательного движения и наоборот. Преобразователь описан
со следующими уравнениями:
T=K·I
V=K·ω
где
В | ||
I | Ток через электрические порты преобразователя | |
T | Крутящий момент | |
| ω | K | Константа пропорциональности |
Блок Rotational Electromechanical Converter представляет
электромеханическое преобразование энергии без потерь, поэтому то же самое
в обоих уравнениях используется постоянная пропорциональности.
Соединения + и – сохраняют электрические порты, соответствующие
к положительной и отрицательной клеммам преобразователя соответственно.
Соединения C и R сохраняют механические поворотные порты. Если
ток, протекающий от плюса к минусу, равен
положительный, то результирующий крутящий момент положительный, действующий от порта C
к порту R. Это направление можно изменить, используя отрицательное значение
для К.
Переменные
Чтобы установить приоритет и начальные целевые значения для переменных блока перед моделированием, используйте
раздел Initial Targets в диалоговом окне блока или свойстве
Инспектор. Для получения дополнительной информации смотрите Приоритет Задания и Начальную Цель для Переменных Блока.
Номинальные значения позволяют указать ожидаемую величину переменной в модели.
Использование масштабирования системы на основе номинальных значений повышает надежность моделирования. Номинальный
значения могут поступать из разных источников, одним из которых является Номинал
Раздел Values в диалоговом окне блока или в инспекторе свойств. Для большего
Для большего
информацию см. в разделе Изменение номинальных значений для переменной блока.
Параметры
- Константа пропорциональности K
Константа пропорциональности для электромеханических преобразований.
Значение по умолчанию:0,1В/(рад/с).
Порты
Блок имеет следующие порты:
-
+ Электрический порт сохранения, связанный с положительным преобразователем
Терминал.-
- Электрический порт сохранения, связанный с отрицательным преобразователем
Терминал.-
C Механический поворотный порт консервации.
-
R Механический поворотный порт консервации.
Расширенные возможности
Генерация кода C/C++
Сгенерируйте код C и C++ с помощью Simulink® Coder™.
История версий
Представлено в R2007a
См.
