Содержание
Помогите решить / разобраться (Ф)
Сообщения без ответов | Активные темы | Избранное
randy |
| ||
23/10/12 |
| ||
| | |||
BISHA |
| |||
08/01/09 |
| |||
| | ||||
miflin |
| ||
27/02/12 |
| ||
| | |||
randy |
| ||
23/10/12 |
| ||
| | |||
_Ivana |
| ||
05/09/12 |
| ||
| | |||
randy |
| ||
23/10/12 |
| ||
| | |||
nestoronij |
| ||
09/02/12 |
| ||
| | |||
randy |
| ||
23/10/12 |
| ||
| | |||
phys |
| ||
05/05/11 |
| ||
| | |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 9 ] |
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
2.
 2. Вычисление скоростей точек тела, совершающего плоскопараллельное движение
2. Вычисление скоростей точек тела, совершающего плоскопараллельное движение
В любой момент времени скорости
любых двух точек плоской фигуры
исвязаны равенством
Рис. 2.3 |
(a)
Вектор
представляет собой скорость, полученную
точкойпри вращении плоской фигуры вокруг оси,
проходящей через полюсперпендикулярно плоской фигуре. Этот
вектор направлен перпендикулярно
отрезку(по касательной к окружности, которую
описывает точкапри вращении тела вокруг оси),
причем в сторону вращения тела (Рис.
2.3). В соответствии с формулой Эйлера
Пример 2.4
Пластина совершает плоскопараллельное
движение.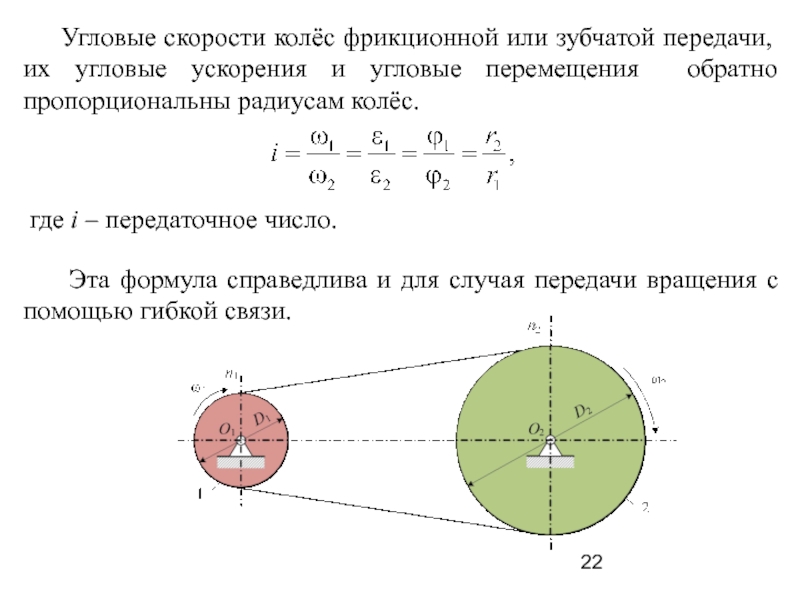 В данный момент времени угловая
В данный момент времени угловая
скорость пластины равна
,
проекция на осьскорости точкипластины равна.
Скорость точкиобразует с осьюугол(Рис. 2.4). Определить модули скоростей
точеки,
если.
Рис. 2.4 |
Запишем уравнение (a)
в проекциях на координатные оси:
или
Учитывая данные задачи, получаем:
или
Отсюда:
Следует заметить, что прямое
использование формулы (a)
целесообразно в довольно небольшом
числе случаев. В некоторых задачах имеет
смысл использовать так называемую
теорему о проекциях. Поскольку векторперпендикулярен отрезку,
из формулы (a) получаем
утверждение:
проекции скоростей концов отрезка,
соединяющего две точки абсолютно
твердого тела, на направление этого
отрезка равны.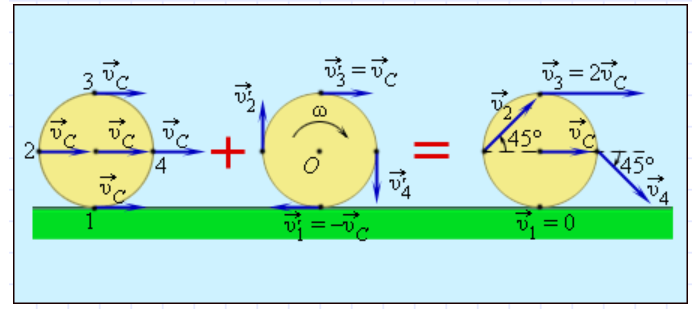
Пример 2.5
Стержень
движется в плоскости рисунка, причём
его конецвсё время находится на полуокружности,
а сам стержень всё время касается
неподвижного выступа,
расположенного на диаметре(Рис. 2.5). Определить скоростьточки стержня, касающейся выступа, в
тот момент времени, когда радиусперпендикулярен,
если известно, что скорость точкив этот момент.
Рис. 2.5 |
Заметим, что направления скоростей
точекив данный момент времени известны.
Скорость точкинаправлена по касательной к траектории,
т.е. по касательной к окружности в нижней
точке. Скорость точкинаправлена вдоль стержня, т.к. по условию
задачи стержень не отрывается от выступа.
Таким образом, для заданного положения
стержня известны углы, которые образуют
векторы скоростей точекис отрезком.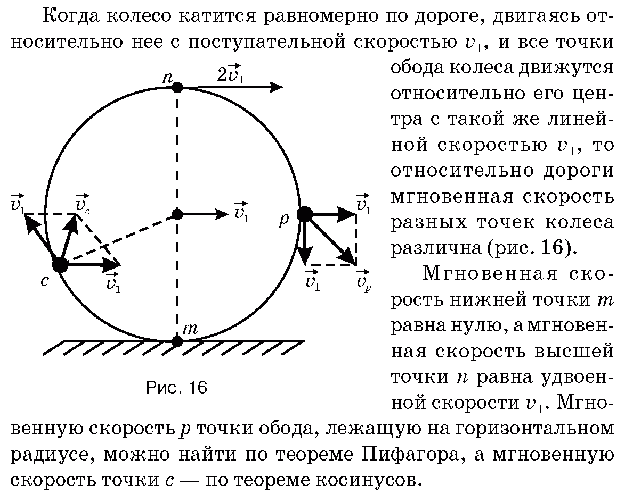
В таком случае целесообразно использовать
теорему о проекциях скоростей:
Решение задач с помощью мгновенного
центра скоростей. Основной способ
определения поля скоростей при
плоскопараллельном движении твёрдого
тела основан на использовании мгновенного
центра скоростей.
Как уже говорилось, за полюс можно
принять любую точку плоской фигуры. В
данный момент времени различные точки
тела имеют разные скорости. За полюс
имеет смысл принимать точку, скорость
которой в данный момент времени равна
нулю.
Точка, принадлежащая плоской фигуре
или неизменно с ней связанная, скорость
которой в данный момент времени равна
нулю, называется мгновенным центром
скоростей.
Рис. 2.6 |
Скорость любой точкиплоской фигуры определяется так же, как
если бы тело вращалось вокруг оси,
проходящей через мгновенный центр
скоростей перпендикулярно плоскости
движения плоской фигуры (Рис. 2.6):
2.6):
Пример 2.6
Кривошипн0-шатунный механизм связан
шарнирно в середине
шатуна со стержнем,
а последний – со стержнем,
который может вращаться вокруг оси.
Определить угловую скорость стержняв указанном на Рис. 2.7 положении механизма,
если точкиирасположены на одной вертикали; угловая
скоростькривошипаравна 8 рад/с,
Рис. 2.7 |
Стерженьвращается вокруг неподвижной оси.
Скорость точкиопределяем по формуле Эйлера:
Движение стержня
плоскопараллельное. Мгновенный центр
скоростей находится в точке.
Учитывая, что скорости точек тела
пропорциональны расстояниям до
мгновенного центра скоростей, получаем:
Отсюда:
Движение стержня
плоскопараллельное.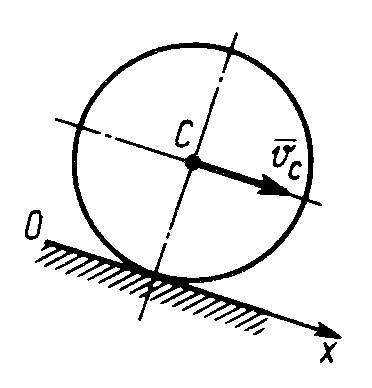 Скорость точкинаправлена по касательной к окружности
Скорость точкинаправлена по касательной к окружности
радиуса,
которая является траекторией точки.
При заданном положении механизма
направление скорости точкисовпадает с направлением стержня.
Для определения скорости точкиимеет смысл использовать теорему о
проекциях скоростей:
Остаётся определить угловую скорость
стержня
.
Поскольку движение этого стержня
вращательное, используем формулу Эйлера:
Пример 2.7
Колесо радиуса
катится без скольжения по неподвижной
поверхности (Рис. 2.8). Скорость центра
колеса.
Определить скорости точеки
Рис. 2.8 |
Мгновенный центр скоростейнаходится в точке касания колеса и
дороги. Зная скорость центра, находим
угловую скорость колеса:
Скорости точек колеса определяем по
формуле Эйлера:
Качение колеса представляет интерес
еще и в том отношении, что позволяет
проиллюстрировать смысл формулы (a).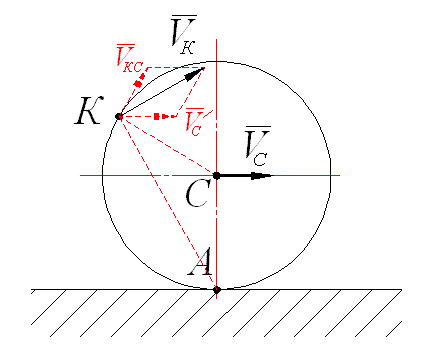
Пусть колесо, движение которого мы
рассматриваем, – ведущее колесо, т.е.
оно принудительно вращается некоторым
приводом. Рассмотрим возможные
режимы движения.
Может случиться так, что колесо
вращается, но автомобиль не перемещается
– буксует. В этом случае движение колеса
представляет собой вращение вокруг
неподвижной оси
.
Все точки колеса будут описывать
окружности с центром в точке,
радиусы которых равны расстояниям от
этих точек до оси колеса. Скорость любой
точки направлена по касательной к этой
окружности и определяется по формуле
Эйлера.
Другое возможное движение колеса
представляет собой качение с
проскальзыванием. Автомобиль при этом
перемещается, но колеса вращаются
несоразмерно быстро. Скорость оси колеса
отлична от нуля и вступает в свои права
формула (a). Скорость,
например, точки,
которая в первом случае была ее полной
скоростью, становится скоростью,
полученной точкойпри вращении колеса вокруг оси.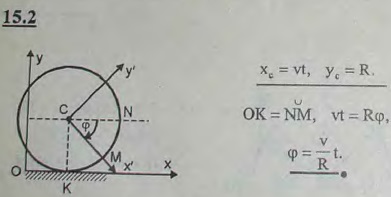
Полная же скорость точкитеперь геометрически складывается из
скорости точкии скорости, полученной точкойпри вращении колеса вокруг оси
Заметим, что в этом случае движение
оси (т.е. автомобиля) и вращение колеса
происходят независимо друг от друга и
каждое из них должно быть задано.
Последний режим движения колеса –
качение без скольжения. Именно этот
случай рассмотрен в примере 2.7. Движение
оси и вращение колеса оказываются
взаимосвязанными. В каждое мгновение
очевидно положение точки, скорость
которой равна нулю. В такой ситуации
при определении скоростей точек колеса
удобнее за полюс брать не точку
,
а мгновенный центр скоростей.
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В
АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 16.3;
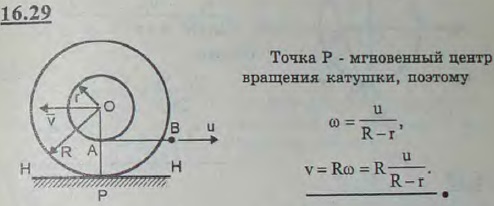
16.10; 16.15; 16.16; 16.19; 16.24; 16.28; 16.29; 16.31;
16.32; 16.33; 16.34; 16.35; 16.36; 16.38; 16.39.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА —
теория и практика»: комплект СР-20.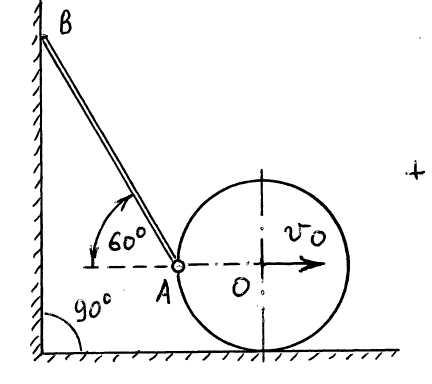
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 6
Пример 2.8
Определить скорость и ускорение ползуна
кривошипного механизма, а также угловую
скорость и угловое ускорение шатунав положении, изображенном на Рис. 2.9.
Кривошипвращается замедленно, имея в данный
момент времени угловую скоростьи угловое ускорение.
Ползун движется по криволинейной
направляющей, имеющей в данном положении
механизма радиус кривизны.
Дано:.
Зная направления скоростей точек
и,
построим мгновенный центр скоростейстержня,
после чего определим угловую скорость
стержня
и скорость точки
Попытка определить угловое ускорение
стержня
,
используя определение
закончится неудачей, поскольку зависимость
неизвестна.
Для определения ускорения точки
принимаем за полюс точку.
Поскольку известны траектории всех
точек во всех их движениях, представим
ускорения точек их составляющими:
Вычислим векторы, входящие в уравнение
.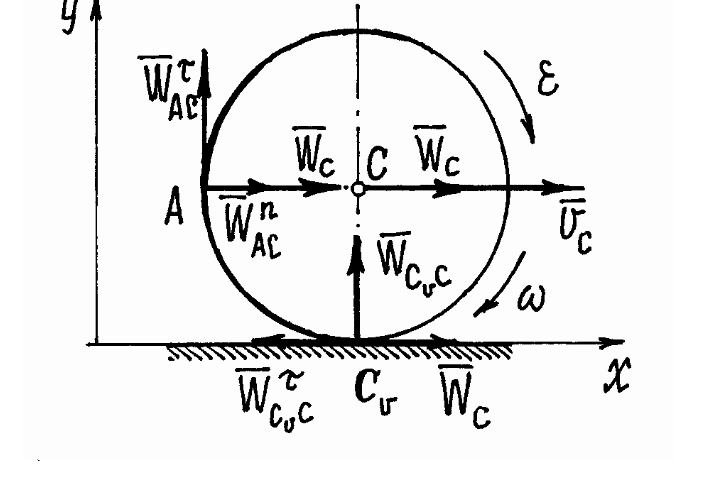
Рис. 2.9 |
Точка
принадлежит вращающемуся телу.
Определяем модули составляющих ускорения
этой точки:
направления векторов показаны на
Рис. 2.9.
Точка
движется по криволинейной направляющей.
Касательное и нормальное ускорения
точкиопределяются по формулам:
направления составляющих ускорения
показаны на Рис. 2.9. По приведенной
формуле не удается вычислить касательное
ускорение точки
,
поскольку неизвестны зависимости
расстоянийиот времени.
Находим составляющие ускорения,
полученного точкой
при вращении шатунавокруг оси.
Заметим, что вращательное ускорение
остается неизвестным по модулю, поскольку
неизвестно угловое ускорение шатуна:
Таким образом, из шести векторов,
входящих в равенство
,
только два неизвестны по модулю. Определим
Определим
эти неизвестные из уравнения.
Это уравнение можно решить аналитически
или геометрически. Рассмотрим оба
способа решения.
Имеет смысл выбрать координатные
оси так, чтобы в каждое уравнение в
проекциях входила только одна неизвестная.
Направим ось
вдоль(перпендикулярно),
а осьпо направлению(перпендикулярно).
Записывая уравнениев проекциях на ось,
получаем:
Отсюда
Отрицательный знак говорит о том,
что предполагаемое направление вектора
было выбрано ошибочно; в действительности
этот вектор направлен в противоположную
сторону.
Записывая уравнение
в проекциях на ось,
получаем:
Отсюда
Рис. 2.10 |
Вычислив,
можем определить угловое ускорение
стержня:
Рассмотрим геометрический способ
решения уравнения
.
Построим в масштабе сумму векторов,
стоящих в правой части уравнения.
От некоторой точкиотложим,
от его конца отложим,
а затем(Рис. 2.10). Остается построить,
модуль которого неизвестен. Проведем
через конецпунктирную прямую, параллельную.
Конец суммы векторов, стоящих в правой
части уравнения,
лежит на этой прямой.
Обратимся к левой части уравнения
.
Отложим от точкиизвестный вектор.
Через его конец проведем пунктирную
прямую, параллельную вектору.
Точка пересечения построенных прямых
определяет положение конца вектора
ускорения точки.
Пример 2.9
Колесо радиуса
катится без скольжения по прямолинейному
пути (Рис. 2.11). Ось колеса движется
ускоренно, имея в данный момент времени
скоростьи ускорение.
Определить проекции ускорение любой
точкиобода колеса на оси координат.
Принимая за полюс точку
,
получаем:
причем
где
– угловая скорость колеса;– его угловое ускорение.
Рис. 2.11 |
Зная положение мгновенного
центра скоростей колеса – точка касания
колеса и дороги, определяем угловую
скорость колеса:
В рассматриваемой задаче расстояние
от точки
,
скорость которой известна, до мгновенного
центра скоростейсо временем не изменяется. Это
обстоятельство позволяет найти угловое
ускорение колеса в данный момент времени
по определению углового ускорения:
,
так как
представляет собой проекцию вектора
ускорения точкина направление её вектора скорости,
которая в рассматриваемом случае равна.
Записывая уравнение
в проекциях на координатные оси, получаем
проекции вектора ускорения точки:
Пример 2. 10
10
Колесо радиуса
катится без скольжения по криволинейной
поверхности (Рис.2.12). Ось колеса движется
ускоренно, имея в данный момент времени
скоростьи касательное ускорение.
Определить проекции ускорения любой
точкиобода колеса на заданные координатные
оси, если радиус кривизны в точкеравен.
Рис. 2.12 |
Задача решается так же, как в
примере 2.9, но в отличие от предыдущей
задачи, траектория точки– кривая линия. У точкипоявляется вторая составляющая ускорения
– нормальная:
В результате получаем:
Пример 2.11
Колесо радиуса
катится без проскальзывания по
прямолинейному пути. Ось колеса движется
равномерно со скоростью(Рис. 2.13). Определить ускорение любой
2.13). Определить ускорение любой
точкиколеса.
Рис. 2.13 |
Ось колеса движется равномерно
и прямолинейно. Следовательно, точка– мгновенный центр ускорений. Для любой
точкиколеса получаем:
Но угловая скорость колеса
постоянна и, следовательно, угловое
ускорение колеса равно нулю.
Тогда
Таким образом, ускорение любой точки
совпадает с осестремительным ускорением,
полученным этой точкой при вращении
колеса вокруг оси, проходящей через
центр колеса
перпендикулярно плоскости движения.
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В
АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 18.11;
18.13; 18.16; 18. 18; 18.22; 18.23; 18.25; 18.26;
18; 18.22; 18.23; 18.25; 18.26;
18.28; 18.37; 18.38; 18.39; 18.40.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА —
теория и практика»: комплекты СР-21;
СР-22.
ПРАКТИЧЕСКИЕ
ЗАНЯТИЯ № 7-8
Калькулятор поступательной скорости центра колеса
✖Эффективный радиус колеса – это радиус части колеса, которая остается недеформированной при качении.ⓘ Эффективный радиус колеса [r d ] | AlnAngstromArpentАстрономическая единицаАттометрAU длиныЯчменьМиллиард светового годаБоровский радиусКабель (международный)Кабель (Великобритания)Кабель (США)КалибрСантиметрЦепьКубит (греческий)Кубит (длинный)Кубит (Великобритания)ДекаметрДециметрРасстояние от Земли до ЛуныРасстояние до Земли от СолнцаЭкваториальный радиус ЗемлиПолярный радиусЭлектронный радиус (классический)EllExa метрFamnFathomFemtometerFermiFinger (Ткань)Ширина пальцевFootFoot (Обследование США)ФурлонгГигаметрРукаШирина рукиГектометрДюймКенКилометрКилопарсекКилоярдЛигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекМетрМикродюймМикрометрМикронМилМиляМиля (Римская)Миля (Обзор США)МиллиметрМиллион Светового ГодаГвоздь (Ткань)НанометрМорская Лига (int)Морская Лига ВеликобританииМорская Миля (Международная) Морская миля (Великобритания)ПарсекОкуньПетаметрПикаПикометрДлина ПланкаТочкаПолюсКварталТростник (Длинный)РодРимский АктусВеревкаРусский АрчинПротяженность ( Ткань)Sun RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | +10% -10% | |
✖Скорость вала двигателя в силовой установке (двигатель или двигатель или их комбинация) — это скорость вращения вала двигателя или коленчатого вала (в случае двигатель ) вращается. | Градус в деньГрадус в часГрадус в минутуГрадус в месяцГрадус в секундуГрадус в неделюГрадус в годРадиан в деньРадиан в часРадиан в минутуРадиан в месяцРадиан в секундуРадиан в неделюРадиан в годРеволюция в деньОборот в часОборот в минутуОборот в секунду | +10% -10% | |
✖Передаточное число трансмиссии – это соотношение между числом оборотов коленчатого вала двигателя и числом оборотов вала, выходящего из коробки передач.ⓘ Gear Rat ио из Трансмиссия [i] | +10% -10% | ||
колес.ⓘ Передаточное число конечной передачи [i или ] | +10% -10% |
✖Скорость поступательного движения — это скорость центра колеса относительно земли. | Сантиметр в часСантиметр в минутуСантиметр в секундуКосмическая скорость ПерваяКосмическая скорость ВтораяКосмическая скорость ТретьяСкорость ЗемлиФут в часФут в минутуФут в секундуКилометр в часКилометр в минутуКилометр в секундуУзелУзел (Великобритания)МахМах (стандарт СИ)Метр в часМетр в минутуМетр в секундуМиль в часМиль в минутуМиль в секунду Миллиметр в деньМиллиметр в ЧасМиллиметр в минутуМиллиметр в секундуМорская миля в деньМорская миля в часСкорость звука в чистой водеСкорость звука в морской воде (20°C и глубина 10 метров)Ярд в часЯрд в минутуЯрд в секунду | ⎘ Копировать |
👎
Формула
Перезагрузить
👍
Поступательная скорость решения центра колеса
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовую единицу
Эффективный радиус колеса: 0,45 метра —> 0,45 метра Преобразование не требуется
Скорость вала двигателя в силовой установке: 4879 оборотов в секунду Минута —> 4879 оборотов в минуту Преобразование не требуется
Передаточное число трансмиссии: 2,55 —> Преобразование не требуется
Передаточное число главной передачи: 2 —> Преобразование не требуется
ШАГ 2: Оценка формулы
ШАГ 3 : Преобразование результата в единицу вывода
45,08185457
Метр в секунду —> 162,294676484449 Километр в час (Проверьте преобразование здесь)
< 13 Калькуляторы механики движения поездов
Поступательная скорость центра колеса
Идти
Скорость поступательного движения = (пи * Эффективный радиус колеса * Скорость вала двигателя в силовой установке) / (30 * Передаточное число трансмиссии * Передаточное число главной передачи)
Функция силы колеса
Идти
Функция силы на колесе = (передаточное число трансмиссии * передаточное число главной передачи * крутящий момент двигателя) / (2 * радиус колеса)
Скорость вращения ведомого колеса
Идти
Скорость вращения ведущих колес = (частота вращения вала двигателя в силовой установке)/(передаточное число трансмиссии * передаточное число главной передачи)
Аэродинамическая сила сопротивления
Идти
Сила сопротивления = Коэффициент сопротивления * ((Плотность массы * Скорость потока ^ 2) / 2) * Базовая площадь
График скорости
Идти
Скорость по расписанию = расстояние, пройденное поездом / (время движения поезда + время остановки поезда)
Пиковая скорость с учетом времени для ускорения
Идти
Пиковая скорость = время ускорения * ускорение поезда
Коэффициент сцепления
Идти
Коэффициент сцепления = Тяговое усилие/Вес поезда
Время ускорения
Идти
Время разгона = максимальная скорость/ускорение поезда
Запланировать время
Идти
Время расписания = время движения поезда + время остановки поезда
Задержка поезда
Идти
Замедление поезда = максимальная скорость/время замедления
Время для замедления
Идти
Время замедления = максимальная скорость/замедление поезда
Градиент поезда для правильного движения транспорта
Идти
Градиент = грех (угол D) * 100
Ускоряющийся вес поезда
Идти
Ускоряющий вес поезда = вес поезда * 1,10
Формула поступательной скорости центра колеса
Скорость поступательного движения = (пи * Эффективный радиус колеса * Скорость вала двигателя в силовой установке) / (30 * Передаточное число трансмиссии * Передаточное число главной передачи)
V t = (pi*r d *N pp )/(30*i*i o )
Разница между вращательным и поступательным движением?
Поступательное движение. Поступательное движение — это движение, которое включает скольжение объекта в одном или нескольких из трех измерений: x, y или z. Но объект все еще может двигаться, даже если он просто находится в определенных координатах x, y и z, он все еще может вращаться.
Поступательное движение — это движение, которое включает скольжение объекта в одном или нескольких из трех измерений: x, y или z. Но объект все еще может двигаться, даже если он просто находится в определенных координатах x, y и z, он все еще может вращаться.
Вращательное движение. Вращательное движение — это непрерывное вращение объекта вокруг внутренней оси. Конькобежец может сделать это, вращаясь на месте. Она отдаст себе вращательную энергию. И поскольку энергия всегда сохраняется, а меньший объект должен вращаться быстрее, чтобы иметь ту же энергию, когда она приближает руки к своему телу, скорость ее вращения будет увеличиваться — вращение будет становиться все быстрее и быстрее.
Как рассчитать поступательную скорость центра колеса?
Калькулятор поступательной скорости центра колеса использует Поступательная скорость = (pi * Эффективный радиус колеса * Скорость вала двигателя в силовой установке) / (30 * Передаточное число трансмиссии * Передаточное число главной передачи) для расчета поступательной скорости, Поступательная скорость Формула скорости центра колеса определяется как линейная скорость, с которой будет перемещаться центр колеса относительно земли, и вычисляется относительно скорости силовой установки, полезного радиуса и передаточных чисел трансмиссии и бортовой передачи. Поступательная скорость обозначается В т символ.
Поступательная скорость обозначается В т символ.
Как рассчитать поступательную скорость центра колеса с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для поступательной скорости центра колеса, введите эффективный радиус колеса (r d ) , скорость вала двигателя в силовой установке (N pp ) , передаточное отношение трансмиссии (i) & Передаточное число главной передачи (i o ) и нажмите кнопку расчета. Вот как можно объяснить расчет поступательной скорости центра колеса с заданными входными значениями -> 584,2608 = (пи*0,45*510,927685202802)/(30*2,55*2) .
Часто задаваемые вопросы
Что такое поступательная скорость центра колеса?
Формула поступательной скорости центра колеса определяется как линейная скорость, с которой центр колеса будет перемещаться относительно земли, и вычисляется относительно скорости силовой установки, эффективного радиуса и передаточных чисел трансмиссии и конечной диск и представлен как V t = (pi*r d *N pp )/(30*i*i o ) или Поступательная скорость = (pi*действующий радиус колеса*скорость вращения вала двигателя в силовой установке )/(30*Передаточное число коробки передач*Передаточное число главной передачи) . Эффективный радиус колеса — это радиус части колеса, которая остается недеформированной во время качения. Скорость вала двигателя в силовой установке (двигатель или двигатель или их комбинация) — это скорость вращения, с которой вал двигателя или коленчатый вал (в случае двигатель) вращается, Передаточное отношение трансмиссии — это отношение между оборотами коленчатого вала двигателя и оборотами вала, выходящего из коробки передач & Передаточное число главной передачи — это отношение между оборотами вала коробки передач и оборотами вала колеса.
Эффективный радиус колеса — это радиус части колеса, которая остается недеформированной во время качения. Скорость вала двигателя в силовой установке (двигатель или двигатель или их комбинация) — это скорость вращения, с которой вал двигателя или коленчатый вал (в случае двигатель) вращается, Передаточное отношение трансмиссии — это отношение между оборотами коленчатого вала двигателя и оборотами вала, выходящего из коробки передач & Передаточное число главной передачи — это отношение между оборотами вала коробки передач и оборотами вала колеса.
Как рассчитать поступательную скорость центра колеса?
Формула поступательной скорости центра колеса определяется как линейная скорость, с которой центр колеса будет перемещаться относительно земли, и вычисляется относительно скорости силовой установки, эффективного радиуса и передаточных чисел трансмиссии и конечной привод рассчитывается с использованием Поступательная скорость = (pi * Эффективный радиус колеса * Скорость вала двигателя в силовой установке) / (30 * Передаточное число трансмиссии * Передаточное число главной передачи) . Чтобы рассчитать поступательную скорость центра колеса, вам потребуется эффективный радиус колеса (r d ) , частота вращения вала двигателя в силовой установке (N pp ) , передаточное число трансмиссии (i) и передаточное число конечной передачи (i или ) . С помощью нашего инструмента вам необходимо ввести соответствующие значения эффективного радиуса колеса, частоты вращения вала двигателя в силовой установке, передаточного отношения трансмиссии и передаточного числа главной передачи и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Чтобы рассчитать поступательную скорость центра колеса, вам потребуется эффективный радиус колеса (r d ) , частота вращения вала двигателя в силовой установке (N pp ) , передаточное число трансмиссии (i) и передаточное число конечной передачи (i или ) . С помощью нашего инструмента вам необходимо ввести соответствующие значения эффективного радиуса колеса, частоты вращения вала двигателя в силовой установке, передаточного отношения трансмиссии и передаточного числа главной передачи и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Поделиться
Скопировано!
домашнее задание и упражнения — Если автомобиль движется с определенной скоростью, с какой скоростью вращается его колесо?
спросил
Изменено
8 лет, 5 месяцев назад
Просмотрено
3к раз
$\begingroup$
Допустим, в данном случае автомобиль движется со скоростью $v$ и рассмотрим любое колесо автомобиля. Как быстро движется и ? Верно ли, что центр колеса движется с той же скоростью, что и автомобиль, то есть $v$? Почему это?
Как быстро движется и ? Верно ли, что центр колеса движется с той же скоростью, что и автомобиль, то есть $v$? Почему это?
Колесо соединено с автомобилем через ось, которая проходит через центр круга, который является нашим колесом. Точка, которая соприкасается с землей, является мгновенным центром вращения , и именно эта точка на колесе имеет нулевую скорость. Ясно, что центр колеса имеет ненулевая скорость.
Итак, в любой момент движение есть вращение вокруг неподвижной оси, где неподвижная ось в рассматриваемый момент лежит в точке контакта с землей, а скорость равна нулю на неподвижной оси. Если угловая скорость колеса $\omega$ и колесо имеет радиус $R$, то скорость в центре колеса $v_C = \omega R$.
Почему эта скорость $v_C = \omega R$ такая же, как скорость автомобиля $v$? Может быть, это самоочевидно, но я действительно не понимаю, почему.
- домашние задания и упражнения
- скорость
- скорость
- вращательная кинематика
- угловая скорость
$\endgroup$
2
$\begingroup$
В системе отсчета автомобиля ось неподвижна, но земля движется под ней со скоростью $v_C$.
 11.2012, 20:07
11.2012, 20:07  11.2012, 20:40
11.2012, 20:40 
 А откуда радиус-то появился?
А откуда радиус-то появился?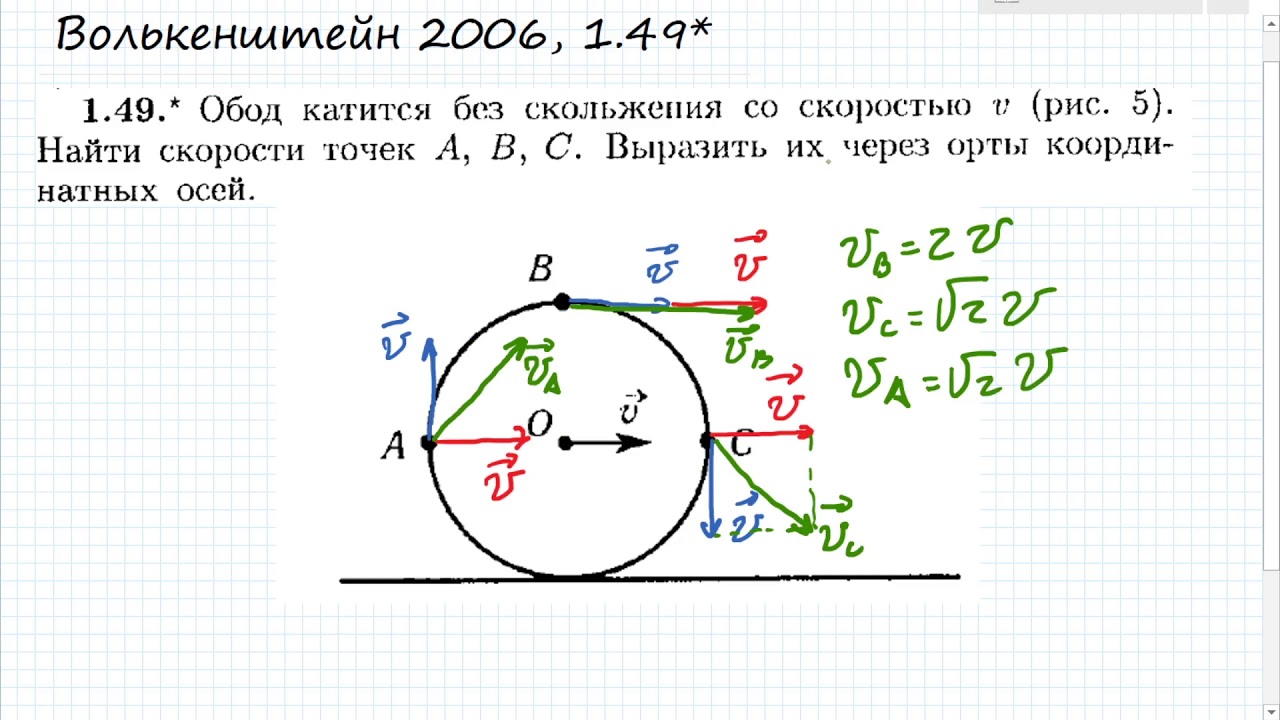 11.2012, 10:48
11.2012, 10:48 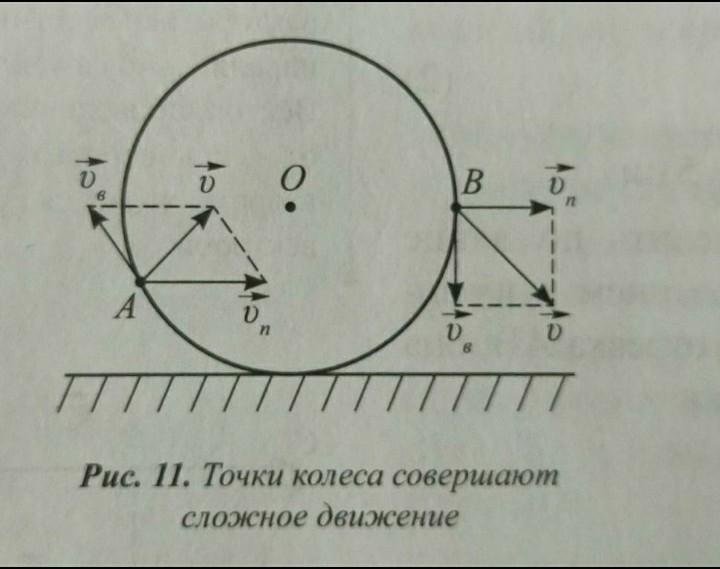 11.2012, 14:49
11.2012, 14:49 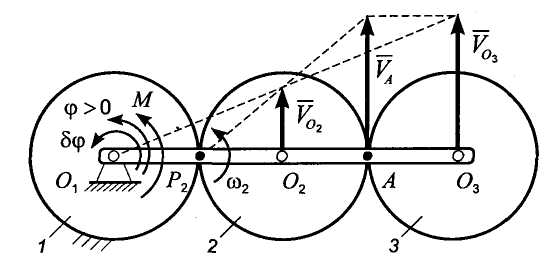
 ⓘ Скорость вала двигателя в силовой установке [N pp ]
ⓘ Скорость вала двигателя в силовой установке [N pp ] Ее также называют линейной скоростью.ⓘ Поступательная скорость центра колеса [V t ]
Ее также называют линейной скоростью.ⓘ Поступательная скорость центра колеса [V t ]