5. Постоянная времени

характеризует
длительность протекания переходного
процесса,
обычно это тот промежуток времени, в
течение которого реакция схемы на
единичный скачок убывает в «е»
раз (е≈2.718) и напряжение достигает 63,2 %
своего установившегося значения.
Постоянная времени связана с граничной
частотой, либо с частотой пропускания
фильтра
нижних частот.

.

6.Какие позитивные или негативные последствия переходных процессов в электрических приборах и системах.

При
коммутационных операциях выключателями
и разъединителями в
сети
высокого напряжения возникает
высокочастотный (ВЧ) переходный
процесс.
Параметры этого процесса индивидуальны
для каждого объекта и, более того, даже
для каждой конкретной коммутации. ВЧ
токи и
перенапряжения
через системы шин распространяются по
частям объекта. Они
создают
электромагнитные поля, способные
вызывать наводки во вторичных
кабелях
и даже во внутренних цепях аппаратуры.
Кроме того, проникновение
коммутационных
помех во вторичные кабели происходит
через трансформатор
тока,
трансформатор напряжения и т.п. Особенно
серьезна ситуация в
пускателях
взрывозащищенного исполнения, где
высоковольтное оборудование
и
подверженная влиянию электронная
аппаратура размещаются очень близко
друг
к другу.

Переходные
процессы являются причиной искажения
формы импульсов при прохождении их
через линейные цепи. Расчет и анализ
устройств автоматики, где происходит
непрерывная смена состояния электрических
цепей, немыслим без учета переходных
режимов.

В
ряде устройств возникновение переходных
процессов, в принципе, нежелательно и
опасно. Расчет переходных режимов в
этих случаях позволяет определить
возможные перенапряжения и увеличения
токов, которые во много раз могут
превышать напряжения и токи стационарного
режима. Это особенно важно для цепей со
значительной индуктивностью или большой
емкостью.

Тема 5. Основы теории четырехполюсников

1. Какая электрическая цепь называется четырехполюсником?

Четырехполюсник
— это электрическая цепь произвольной
конфигурации, которая имеет две пары
внешних зажимов (рис.5.1): два входных
зажима 1-2 для подключения источников и
два выходных зажима 1`-2` для подключения
приемников.

Рисунок
5.1 — Условное обозначение четырехполюсника
с подключенным источником

и приемником
.

Четырехполюсники
подразделяются на две группы — пассивные
и активные. Пассивный четырехполюсник
— это четырехполюсник, цепь которого
содержит только пассивные элементы
(например, трансформатор, пассивный
фильтр и т. п.). Активный четырехполюсник
— это четырехполюсник, цепь которого
включает независимые и зависимые
источники (например, транзисторный
усилитель, активный фильтр и т. п.).

2. Назовите формы записи уравнений четырехполюсника.

   

Уравнения
четырехполюсников — это зависимости
между двумя напряжениями и двумя токами,
которые определяют режим на первичных
и вторичных выводах четырехполюсника.

Уравнения
четырехполюсников выводятся на основе
рассмотрения цепи с одним источником
и нагрузкой (рис.5.1), для которой
составляется система уравнений по МКТ.
В результате получают пару уравнений
с четырьмя неизвестными. Описание цепи
по МКТ и последующие преобразования
позволяют определить шесть различных
математически эквивалентных вариантов
записи уравнений четырехполюсников в
формах A,
Z,
Y,
H,
G,
B.
Одна из них:

—
коэф.передачи
напряж. при х.х.на 2-2`

—
передат.сопр.
при к.з. 2-2`.

—
передат.пров. при х.х. на 2-2`

—
коэф.
передачи тока при к.з. 2-2`

1.5 Постоянная времени цепи и ее физический смысл

Закон
изменения множителя
зависит от величины.
Эта величина имеет размерность времени
и называется постоянной времени цепи.
Обозначается постоянная времени
греческой буквой .

Через
5
после коммутации любой ток или напряжение
цепи достигает 99,3% от своего предельного
значения (при t
).
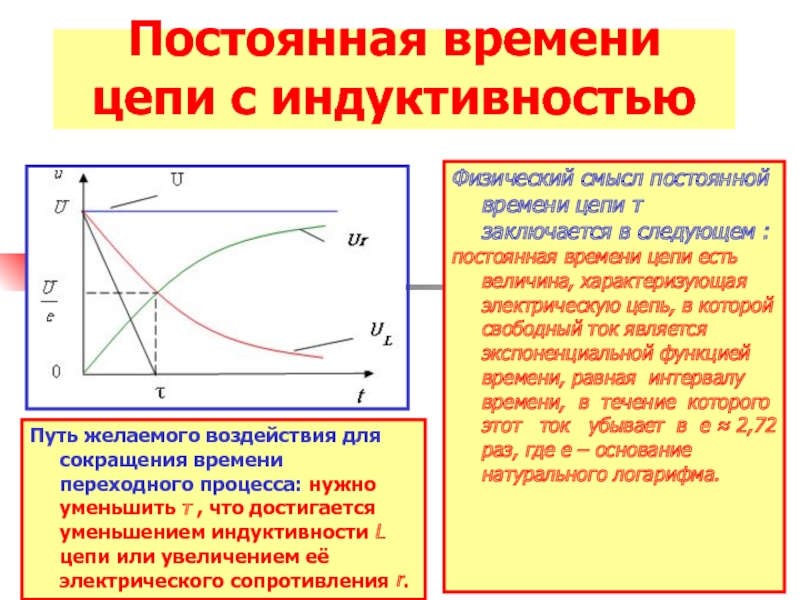
В неразветвленной RL-
цепи (рис.1.2):

(1.15)

Таким
образом, имеем решение для i_L(t)
при 0₊,
т.е. при всех t
переходного процесса:

.
(1.16)

Определяем
напряжение на резисторе R
и индуктивности L
в переходном режиме:

(1.17)

(1.18)

По
формулам (1.17),
(1.18) построим
графики изменения напряжений от времени
t.

1

2

3

4

Рис. 1.4

Из
рис. 1.4 видно, что при любом значении t
сумма напряжений u_R
и u_L
составляет величину входного напряжения
U,
что подтверждает второй закон Кирхгофа.

Анализ
полученных результатов показывает, что
при нулевых начальных условиях в момент
t=0₊
индуктивность ведет себя как бесконечно
большое сопротивление (разрыв цепи), а
при t,
как бесконечно малое сопротивление
(короткое замыкание цепи).

Постоянная
времени τ
– это время, в течение которого свободная
составляющая i_св
изменяется ровно в “e”
раз. Покажем это. Для этого сравним два
значения i_св
при
произвольном времени t,
взятых через время τ:

Таким
образом, величина τ
определяет скорость протекания
переходного процесса в цепи, т.к. через
(45)τ
он обычно практически заканчивается.

2.Расчет прохождения сигнала через линейные электрические цепи

Параметры сигнала:

длительность
импульса: 0,4 мс; период сигнала: 1,5 мс;
середина импульса: 0,014 мс; максимальное
и минимальное значение сигнала: 0,5 и 0
В.

2.1Разложение импульсных колебаний на гармонические составляющие

Результат
воздействия на электрическую цепь
синусоидального напряжения и тока можно
найти при помощи символического метода
решения уравнений Кирхгофа. Форма
синусоидального напряжения (или тока)
на выходе любой линейной электрической
цепи остается синусоидальной, а амплитуда
напряжений и его начальная фаза
изменяются. Поэтому при рассмотрении
воздействия на электрические цепи
несинусоидальных напряжений (токов) во
многих случаях целесообразно представить
их в виде некоторой суммы синусоидальных
колебаний.

Любое
периодическое несинусоидальное колебание
можно разложить в бесконечный
тригонометрический ряд, состоящий из
постоянной составляющей и синусоидальных
составляющих различной частоты, амплитуды
и фазы. Совокупность этих синусоидальных
или гармонических составляющих называется
частотным спектром.

Тригонометрический
ряд, получающийся при разложении
периодических несинусоидальных
колебаний, называется рядом Фурье [7,
с.7]:

Коэффициенты
ряда Фурье ( А₀,
a_k,
b_k
и
φ_k
)
рассчитываем по формулам [7, c.7]:

Где

f(t)
– несинусоидальная периодическая
функция;

Т
– период колебаний, т.е. наименьшее
время, по истечении которого колебания
полностью повторяются, 1/с;

ω₁
– скорость изменения фазы (угловая
частота) первой или основной гармоники,
рад/с;

k
– порядковый номер гармоники.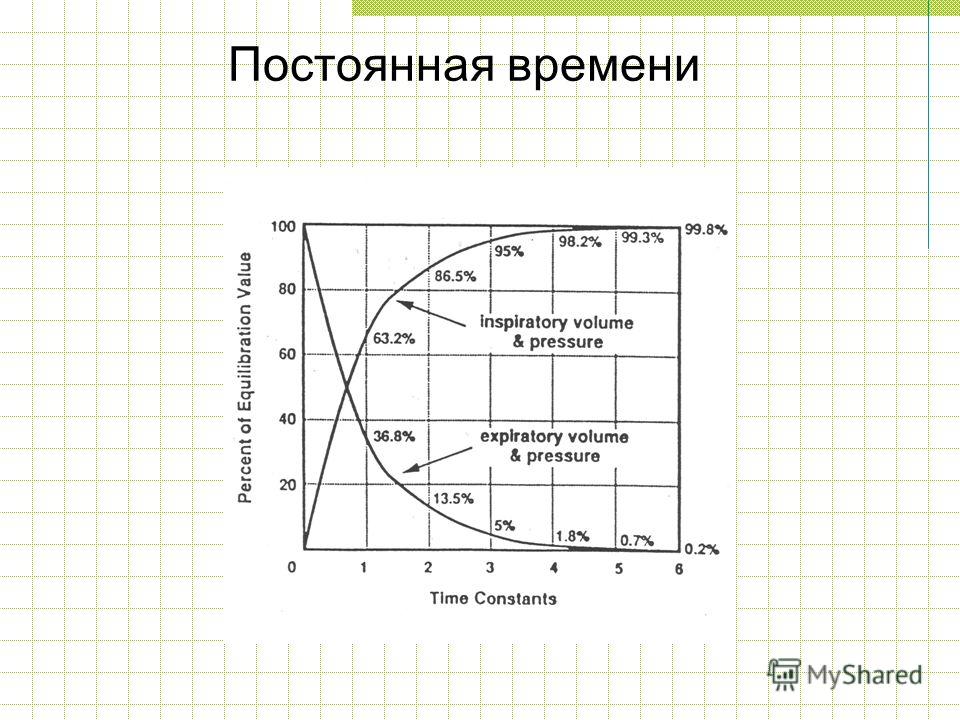

В
радиотехнике для определения отклика
цепи на негармоническое воздействие
f(t)
используют косинусную форму ряда Фурье
[1, с.276]:

которая
связана с рядом Фурье (2.1) следующими
соотношениями [1, с.276]:

где
A_mk
–это амплитуда
«k»-ой
гармоники, функция четная относительно
частоты;

φ_k
– начальная
фаза «k»-ой
гармоники, функция нечетная относительно
частоты и поэтому может принимать как
положительные значения, так и отрицательные;

А₀
– постоянная составляющая воздействия
f(t).

Амплитуды
всех гармоник разложения (A_mk)
вместе с постоянной составляющей
разложения (А₀)
образуют амплитудно-частотный спектр
(АЧС) воздействия f(t).

Начальные
фазы всех гармоник разложения (ψ_k)
образуют фазо-частотный спектр (ФЧС)
воздействия f(t).

Заданный импульс
напряжения выражается в пределах одного
периода функцией

0,5,

f(t)=

0,

т.е.
мы имеем импульсное напряжение
прямоугольной формы с периодом повторения
Т и длительностью импульса τ_И
со смещением середины импульса
относительно оси ординат.

Интегрирование
проводим в пределах от 0 до,
введя перед интегралом множитель 2.

Постоянная
составляющая ряда на основании формулы
(2.2) будет равна

Коэффициенты
а_k,
b_k
(формулы (2.3) и (2.4))
:

Рассчитываем
коэффициенты (амплитуды гармоник) при
косинусных составляющих ряда Фурье, а
также начальные фазы гармоник:

Тогда

Учитывая
то, что[2,
c. 98],

Подставляя
численные значения в формулы, получим
амплитуды и начальные фазы гармонических
составляющих ряда Фурье.

Таким
образом рассчитывают периодические
колебания функций четных относительно
частоты. При смещении момента отсчета
времени на любую величину, т.е. при
запаздывании или опережении процесса
на время t₀,
учитываем смещение середины импульса
относительно оси ординат. Смещение
периодической функции не изменяет
значений амплитуд гармоник. Начальные
фазы гармоник изменяются на угол
[2,с.276],

где
t₀
– время начала переднего фронта импульса.

t₀=—t_{смещения}=
— 0,2+0,014= — 0,186,

т.е.
начальные фазы гармонических составляющих
сигнала воздействия рассчитываются по
формуле:

.

Рассчитаем
постоянную составляющую

,

и
амплитуды и начальные фазы гармонических
составляющих:

для
первой гармоники (k=1)

для
второй гармоники (k
=2)

для
третьей гармоники (k
=3)

для
четвертой гармоники (k
=4)

для
пятой гармоники (k
=5)

для
шестой гармоники (k
=6)

для
седьмой гармоники (k
=7)

для
восьмой гармоники (k
=8)

для
девятой гармоники (k
=9)

для
десятой гармоники (k
=10)

Амплитудный
и фазовый спектр сигнала воздействия
изображен на рис. 2.1

Постоянная времени и ее значение

Резисторно-конденсаторные цепи не существуют в стабильных состояниях постоянно. Возможны колебания их состояния из-за изменения уровней напряжения и входа. Это может быть сделано путем размыкания или замыкания переключателя цепи. RC-цепи требуется некоторое время, чтобы отреагировать на изменения напряжения или входного сигнала. Это связано с наличием резисторов и конденсаторов. Скорость, с которой цепь переходит из одного устойчивого состояния в другое, определяется постоянной времени цепи. Эта постоянная времени является произведением сопротивления цепи в омах и емкости цепи в фарадах. Греческая буква тау представляет его.

Значение постоянной времени

Значение постоянной времени RC-цепи — это время, необходимое для зарядки конденсатора до 63,2% от значения приложенным постоянным напряжением.

𝜏 =RC

Где R – сопротивление цепи, а C – емкость цепи. Он используется в следующих формулах для определения напряжения на конденсаторе в зависимости от времени

• При зарядке до приложенного напряжения от нулевого напряжения (V0): V(t)=V0(1-e-t/𝜏)

Где 𝜏 — постоянная времени RC

• Разрядка до нулевого напряжения (V0): В (t)=V0(e-t/𝜏)

Постоянная времени RC

В RC-цепи сопротивление почти мгновенно реагирует на любое изменение напряжения, приложенного к цепи. Однако резистор не накапливает энергию. Это пассивное устройство, которое рассеивает энергию в виде тепловой энергии. С другой стороны, конденсатор может хранить энергию в виде электростатического поля. Он состоит из двух электродов, которые представляют собой пластины из проводящего материала. Эти пластины разделены изоляционным материалом. Этот материал является диэлектриком и может накапливать электростатическую энергию.

Конденсатор, в отличие от резистора, не может мгновенно реагировать на изменение напряжения, приложенного к цепи. Всегда будет короткий период времени сразу после первого приложения напряжения, чтобы ток цепи и напряжение на конденсаторе изменили состояние. Это означает, что будет определенная задержка в конденсаторе, изменяющем свою накопленную энергию в своем электрическом поле. Это справедливо как для случаев, когда энергия должна быть увеличена, так и для случаев, когда энергия должна быть уменьшена.

Время, необходимое цепи для реагирования на изменения, всегда кратно произведению сопротивления и емкости цепи. Это произведение омов и фарад, записанное в секундах. Следующее уравнение выражает ток, протекающий через конденсатор.

iC =C(dv/dt)

Здесь dv — изменение напряжения, а dt — изменение во времени.

Резисторно-конденсаторная цепь

Если цепь замкнута накоротко в цепи резистор-конденсатор, через нее не протекает ток, поскольку она не подключена к источнику напряжения. Когда переключатель цепи включен, в цепи подается определенное напряжение. В момент включения переключателя полностью разряженный конденсатор действует как короткое замыкание из-за резкого изменения состояния dv/dt.

Заключение

Постоянная времени — это время, за которое конденсатор заряжается примерно до 63,2% своего полного значения через резистор, подключенный к нему последовательно. Постоянная времени RC (𝜏) является произведением сопротивления цепи (R) и емкости цепи (C).

𝜏 =RC

И наоборот, постоянная времени также может быть определена как время, затрачиваемое конденсатором, подключенным последовательно к резистору, примерно до 36,8% от его полного значения. Это важное значение, потому что оно означает скорость роста или затухания цепи. Чем ниже значение постоянной времени цепи, тем выше скорость роста или затухания цепи. И чем выше значение постоянной времени цепи, тем ниже скорость нарастания или спада.

Постоянная времени RC-цепи: Определение

Если вы когда-нибудь видели автоматический резак для бумаги, вы, вероятно, задавались вопросом, как люди, работающие с этими устройствами, никогда не теряют палец или руку. Удивительно, но ответ на ваш вопрос содержится в постоянной времени RC-цепей! Это позволяет оператору машины щелкнуть выключателем «вкл.», а затем убрать руки от бумаги задолго до того, как резак для бумаги действительно начнет резать. Продолжайте читать, чтобы узнать больше о том, как эта временная задержка создается постоянной времени в RC-цепях.

Определение постоянной времени в RC-цепи

Чтобы понять, что такое постоянная времени RC-цепи, нам сначала нужно убедиться, что мы знаем, что такое RC-цепь.

Резистивно-емкостная цепь представляет собой электрическую цепь, содержащую сопротивления и конденсаторы.

Как и все другие электрические цепи, каждая RC-цепь, с которой вы столкнетесь, имеет общее сопротивление \(R\) и общую емкость \(C\). Теперь мы можем определить, что такое постоянная времени в такой цепи.

Постоянная времени \(\tau\) в RC-цепи определяется произведением полного сопротивления на общую емкость, \(\tau=RC\).

Проверим работоспособность агрегатов. Мы знаем, что емкость — это заряд \(Q\), деленный на напряжение \(V\), а сопротивление — это напряжение, деленное на ток \(I\). Таким образом, единицами измерения емкости являются \(\mathrm{\tfrac{C}{V}}\), а единицами сопротивления являются \(\mathrm{\tfrac{V}{A}}\). Следовательно, единицы постоянной времени равны 9.0003

\[\ mathrm {\ frac {C} {V}} \ mathrm {\ frac {V} {A}} = \ mathrm {\ frac {C} {A}} = \ mathrm {\ frac {A \ ,s}{A}}=\mathrm{s}.\]

Мы видим, что единицы постоянной времени действительно являются единицами времени!

Определение постоянной времени RC-цепи

Чтобы найти постоянную времени конкретной RC-цепи, нам нужно найти эквивалентное полное сопротивление и емкость цепи. Давайте вспомним, как мы их находим.

Чтобы найти эквивалентное общее сопротивление \(R\) \(n\) резисторов \(R_1,\dots,R_n\), соединенных последовательно, мы просто складываем их индивидуальные сопротивления: 9n C_i.\]

Обратите внимание, что способ сложения сопротивлений и емкостей точно переключается для одного и того же типа соединения!

Когда вы можете упростить схемы с помощью этих правил, заменив несколько резисторов и конденсаторов только одним резистором и одним конденсатором, у вас есть ключ к нахождению постоянной времени! Это связано с тем, что после упрощения у вас есть два магических значения для \(R\) и \(C\), эквивалентное общее сопротивление и емкость, поэтому вы можете просто перемножить эти значения, чтобы получить постоянную времени в соответствии с 9.0003

\[\tau=RC.\]

Получение постоянной времени RC-цепи

Чтобы понять, откуда берется эта постоянная времени, рассмотрим простейшую возможную схему, содержащую резисторы и конденсаторы, а именно схему, содержащую только один резистор и только один конденсатор (так что без батареи!), как показано на рисунке ниже.

Рис. 1. Простая схема, содержащая только конденсатор и резистор.

Допустим, мы начинаем с некоторого ненулевого напряжения \(V_0\) на конденсаторе с емкостью \(C\). Это означает, что по обе стороны конденсатора есть заряд \(Q_0\), и эти две стороны соединены друг с другом цепью, содержащей резистор с сопротивлением \(R\). Таким образом, будет протекать ток с одной стороны на другую сторону конденсатора, вызванный напряжением на нем. Этот ток изменит заряды \(Q\) по обе стороны конденсатора, поэтому он также изменит напряжение! Это означает, что мы хотим посмотреть на напряжение \(V\) на конденсаторе и заряд \(Q\) по обе стороны от него как на функцию времени. Напряжение на конденсаторе равно

\[V=\frac{Q}{C},\]

, поэтому ток \(I\) в цепи равен

\[I=\frac{V}{R}=\frac {Q}{RC}.\]

Но ток представляет собой изменение заряда во времени, поэтому он фактически равен производной по времени от заряда \(Q\) с обеих сторон конденсатора! Важно отметить, что суммарный заряд по обе стороны конденсатора уменьшается с (положительным) током, поэтому в нашем уравнении есть знак минус:

\[\frac{\mathrm{d}Q}{\mathrm {d}t}=-I=-\frac{Q}{RC}.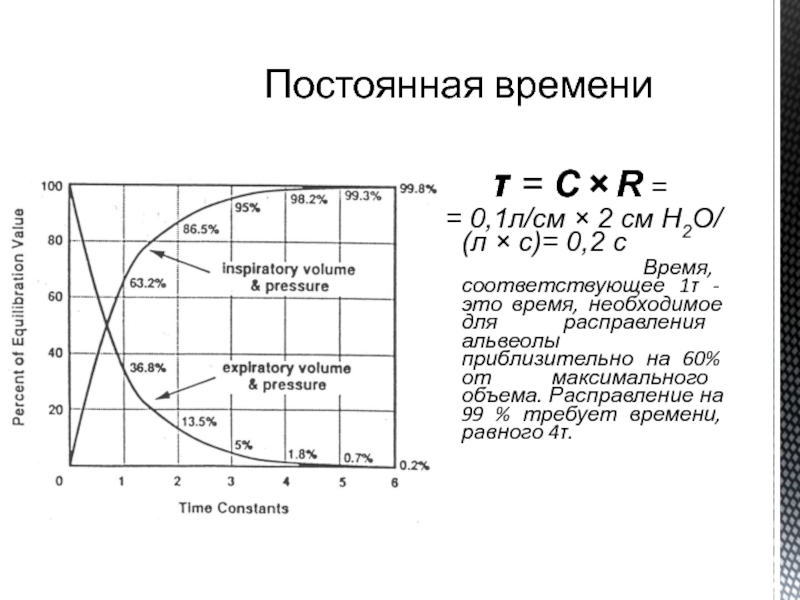 \] 9{-\tfrac{t}{RC}}.\]

Вот и все! Множитель \(RC\) просто говорит нам, насколько быстро идет этот процесс балансировки заряда конденсатора. Через время \(t=\tau=RC\) заряд по обе стороны конденсатора равен

\[Q(\tau)=\frac{1}{\mathrm{e}}Q_0,\]

и из уравнения мы видим, что в целом после каждого периода времени \(\tau\) заряд уменьшался с коэффициентом \(\mathrm{e}\).

При таком уменьшении заряда, согласно \(V=\tfrac{Q}{C}\), напряжение на конденсаторе также уменьшается в \(\mathrm{e}\) раз каждый раз длительность \(\ тау\). Пока сопротивление остается постоянным, ток \(I=\tfrac{V}{C}\) также испытывает такое же уменьшение. Таким образом, свойства всей цепи (заряд по обе стороны от конденсатора, ток в цепи и напряжение на конденсаторе) изменяются с коэффициентом \(\mathrm{e}\) каждый раз, когда длительность \(\tau\ )!

Постоянная времени RC-цепи с батареей

Рис. 2. Та же схема, но теперь она содержит батарею, которая подает напряжение.

Но что делать, если в схеме есть батарейка, как и в большинстве схем? Ну, тогда мы можем начать с конденсатора с нулевым зарядом с обеих сторон: это конденсатор, на котором нет напряжения. Если мы подключим его к батарее, напряжение будет переносить заряды на конденсатор, так что со временем на конденсаторе будет создаваться напряжение. Это напряжение \(В\) со временем будет выглядеть так: 9{-\tfrac{t}{RC}}\right).\]

В этой формуле мы видим ту же экспоненциальную зависимость, но теперь она идет в другую сторону: напряжение на конденсаторе растет.

При \(t=0\,\mathrm{s}\) имеем \(V(0\,\mathrm{s})=0\,\mathrm{V}\), как и ожидалось. На конденсаторе нет сопротивления ни от каких зарядов, поэтому на старте конденсатор ведет себя как «голый провод» с нулевым сопротивлением. Только после запуска, когда на конденсаторе накапливается заряд, для схемы становится очевидным, что это действительно конденсатор! Становится все труднее и труднее добавлять заряд к конденсатору, поскольку заряд на нем и, следовательно, электрическая сила, противодействующая току, растет.

По прошествии длительного времени (множественного постоянной времени \(\tau\)) экспонента приближается к нулю, а напряжение на конденсаторе приближается к \(V(\infty)=V_0\). Постоянное напряжение на конденсаторе также означает, что заряд на пластине постоянен, поэтому в конденсатор и из него не течет ток. Это означает, что конденсатор ведет себя как резистор с бесконечным сопротивлением.

• После включения аккумулятора конденсатор ведет себя как оголенный провод с нулевым сопротивлением.
• По прошествии длительного времени конденсатор ведет себя так, как будто это резистор с бесконечным сопротивлением.

Постоянная времени RC-цепи из графика

Все это означает, что мы должны быть в состоянии определить постоянную времени RC-цепи, если у нас есть график либо напряжения на конденсаторе, либо заряда по обе стороны конденсатор, или полный ток через цепь по отношению ко времени.

Ниже мы видим график напряжения на конденсаторе в цепи, показанной на рисунке 2. Сопротивление резистора равно \(12\,\mathrm{\Omega}\). Какова емкость конденсатора?

Рис. 3. Этот график зависимости напряжения на конденсаторе от времени дает нам достаточно информации для определения постоянной времени цепи.

Из рисунка видно, что напряжение на конденсаторе равно \(\left(1-\tfrac{1}{\mathrm{e}}\right)V_0\) (около \(63\%\)) в момент времени \(t=0,25\,\mathrm{s}\). Это означает, что постоянная времени этой RC-цепи равна \(\tau=0,25\,\mathrm{s}\). Мы также знаем, что \(\tau=RC\), поэтому емкость конденсатора равна

\[C=\frac{\tau}{R}=\frac{0,25\,\mathrm{s}}{12 \,\mathrm{\Omega}}=21\,\mathrm{мФ}.\]

Значение постоянной времени в RC-цепи

Тот факт, что в RC-цепи имеется характеристическая постоянная времени, очень полезен. Как видно из формул и графиков, в основном существует временная задержка напряжения на конденсаторе. Эту временную задержку можно использовать для получения временной задержки напряжения при любом параллельном соединении. Таким образом, вы можете создать временную задержку между поворотом выключателя и включением машины. Это особенно полезно в отраслях с высоким риском, где задержки могут избежать травм.

RC-цепь часто используется в (старых моделях) резаков для бумаги. Это создает временную задержку, так что у человека, использующего машину, есть некоторое время, чтобы убрать руки из опасной зоны после нажатия выключателя.

Постоянная времени RC-цепи — основные выводы

• RC-цепь — это цепь, содержащая резисторы и конденсаторы.
• Постоянная времени RC-цепи определяется произведением общего сопротивления на общую емкость: \[\tau=RC.\]
• Постоянная времени говорит нам, как быстро разряжается конденсатор, если он подключен только к резистору и ни к чему другому, и начинает заряжаться.
• Постоянная времени говорит нам, как быстро заряжается конденсатор, если он подключен к резистору и батарее и начинает работу незаряженным.
  • Сразу после включения аккумулятора конденсатор ведет себя так, как будто это оголенный провод с нулевым сопротивлением.
  • По прошествии длительного времени конденсатор ведет себя так, как будто это резистор с бесконечным сопротивлением.
• Если в цепи есть несколько резисторов или несколько конденсаторов, убедитесь, что вы сначала определили эквивалентное общее сопротивление и емкость, а затем умножили эти значения друг на друга, чтобы получить постоянную времени RC-цепи.