Измерение величин, меры, единицы измерения

  • Меры

  • Единицы измерения

  • Сокращённые наименования мер

  • Измерительные приборы

Величина — это то, что можно измерить. Такие понятия, как длина, площадь, объём, масса, время, скорость и т. д. называют величинами. Величина является результатом измерения, она определяется числом, выраженным в определённых единицах. Единицы, в которых измеряется величина, называют единицами измерения.

Для обозначения величины пишут число, а рядом название единицы, в которой она измерялась. Например,  5 см,  10 кг,  12 км,  5 мин.  Каждая величина имеет бесчисленное множество значений, например длина может быть равна:  1 см,  2 см,  3 см  и т. д.

Одна и та же величина может быть выражена в разных единицах, например килограмм, грамм и тонна — это единицы измерения веса. Одна и та же величина в разных единицах выражается разными числами. Например:

5 см = 50 мм (длина),

1 ч = 60 мин (время),

2 кг = 2000 г (вес).

Измерить величину — значит узнать, сколько раз в ней содержится другая величина того же рода, принятая за единицу измерения.

Например, мы хотим узнать точную длину какой-нибудь комнаты. Значит нам нужно измерить эту длину при помощи другой длины, которая нам хорошо известна, например при помощи метра. Для этого откладываем метр по длине комнаты столько раз, сколько можно. Если он уложится по длине комнаты ровно  7  раз, то длина её равна  7  метрам.

В результате измерения величины получается или именованное число, например  12  метров, или несколько именованных чисел, например  5  метров  7  сантиметров, совокупность которых называется составным именованным числом.

Меры

В каждом государстве правительство установило определённые единицы измерения для различных величин. Точно рассчитанная единица измерения, принятая в качестве образца, называется эталоном или образцовой единицей. Сделаны образцовые единицы метра, килограмма, сантиметра и т. п., по которым изготавливают единицы для обиходного употребления. Единицы, вошедшие в употребление и утверждённые государством, называются мерами.

Меры называются однородными, если они служат для измерения величин одного рода. Так, грамм и килограмм — меры однородные, так как они служат для измерения веса.

Единицы измерения

Ниже представлены единицы измерения различных величин, которые часто встречаются в задачах по математике:

Меры веса/массы:

  • 1 тонна = 10 центнеров;

  • 1 центнер = 100 килограмм;

  • 1 килограмм = 1000 грамм;

  • 1 грамм = 1000 миллиграмм.

Меры длины:

  • 1 километр = 1000 метров;

  • 1 метр = 10 дециметров;

  • 1 дециметр = 10 сантиметров;

  • 1 сантиметр = 10 миллиметров.

Меры площади (квадратные меры):

  • 1 кв. километр = 100 гектарам;

  • 1 гектар = 10000 кв. метрам;

  • 1 кв. метр = 10000 кв. сантиметров;

  • 1 кв. сантиметр = 100 кв. миллиметрам.

Меры объёма (кубические меры):

  • 1 куб. метр = 1000 куб. дециметров;

  • 1 куб. дециметр = 1000 куб. сантиметров;

  • 1 куб. сантиметр = 1000 куб. миллиметров.

Рассмотрим ещё такую величину как литр. Для измерения вместимости сосудов употребляется литр. Литр является объёмом, который равен одному кубическому дециметру  (1 литр = 1 куб. дециметру).

Меры времени:

  • 1 век (столетие) = 100 годам;

  • 1 год = 12 месяцам;

  • 1 месяц = 30 суткам;

  • 1 неделя = 7 суткам;

  • 1 сутки = 24 часам;

  • 1 час = 60 минутам;

  • 1 минута = 60 секундам;

  • 1 секунда = 1000 миллисекундам.

Кроме того, используют такие единицы измерения времени, как квартал и декада.

  • квартал — 3 месяца;

  • декада — 10 суток.

Месяц принимается за  30  дней, если не требуется определить число и название месяца. Январь, март, май, июль, август, октябрь и декабрь —  31  день. Февраль в простом году —  28  дней, февраль в високосном году —  29  дней. Апрель, июнь, сентябрь, ноябрь —  30  дней.

Год представляет собой (приблизительно) то время, в течении которого Земля совершает полный оборот вокруг Солнца. Принято считать каждые три последовательных года по  365  дней, а следующий за ними четвёртый — в  366  дней. Год, содержащий в себе  366  дней, называется високосным, а годы, содержащие по  365  дней — простыми. К четвёртому году добавляют один лишний день по следующей причине. Время обращения Земли вокруг Солнца содержит в себе не ровно  365  суток, а  365  суток и  6  часов (приблизительно). Таким образом, простой год короче истинного года на  6  часов, а  4  простых года короче  4  истинных годов на  24  часа, т. е. на одни сутки. Поэтому к каждому четвёртому году добавляют одни сутки  (29 февраля).

Об остальных видах величин вы узнаете по мере дальнейшего изучения различных наук.

Сокращённые наименования мер

Сокращённые наименования мер принято записывать без точки:





Меры длины

  • Километр — км

  • Метр — м

  • Дециметр — дм

  • Сантиметр — см

  • Миллиметр — мм
Меры веса/массы

  • тонна — т

  • центнер — ц

  • килограмм — кг

  • грамм — г

  • миллиграмм — мг


Меры площади (квадратные меры)

  • кв. километр — км2

  • гектар — га

  • кв. метр — м2

  • кв. сантиметр — см2

  • кв. миллиметр — мм2
Меры объёма (кубические меры)

  • куб. метр — м3

  • куб. дециметр — дм3

  • куб. сантиметр — см3

  • куб. миллиметр — мм3


Меры времени

  • век — в

  • год — г

  • месяц — м или мес

  • неделя — н или нед

  • сутки — с или д (день)

  • час — ч

  • минута — м

  • секунда — с

  • миллисекунда — мс
Мера вместимости сосудов

  • литр — л




1 мм1 см1 дм1 м1 км
1 мм21 см21 дм21 м21 км2
1 мм31 см31 дм31 м31 км3

Измерительные приборы

Для измерения различных величин используются специальные измерительные приборы. Одни из них очень просты и предназначены для простых измерений. К таким приборам можно отнести измерительную линейку, рулетку, измерительный цилиндр и др. Другие измерительные приборы более сложные. К таким приборам можно отнести секундомеры, термометры, электронные весы и др.

Измерительные приборы, как правило, имеют измерительную шкалу (или кратко шкалу). Это значит, что на приборе нанесены штриховые деления, и рядом с каждым штриховым делением написано соответствующее значение величины. Расстояние между двумя штрихами, возле которых написано значение величины, может быть дополнительно разделено ещё на несколько более малых делений, эти деления чаще всего не обозначены числами.

Определить, какому значению величины соответствует каждое самое малое деление, не трудно. Так, например, на рисунке ниже изображена измерительная линейка:

Цифрами  1,  2,  3,  4  и т. д. обозначены расстояния между штрихами, которые разделены на  10  одинаковых делений. Следовательно, каждое деление (расстояние между ближайшими штрихами) соответствует  1 мм.   Эта величина называется ценой деления шкалы измерительного прибора.

Перед тем как приступить к измерению величины, следует определить цену деления шкалы используемого прибора.

Для того чтобы определить цену деления, необходимо:

  1. Найти два ближайших штриха шкалы, возле которых написаны значения величины.

  2. Вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.

Пример:

Определим цену деления шкалы термометра, изображённого на рисунке слева.

Возьмём два штриха, около которых нанесены числовые значения измеряемой величины (температуры).

Например, штрихи с обозначениями  20 °С  и  30 °С.  Расстояние между этими штрихами разделено на  10  делений. Таким образом, цена каждого деления будет равна:

(30 °С — 20 °С) : 10 = 1 °С

Следовательно, термометр показывает  47 °С.

Измерять различные величины в повседневной жизни приходится постоянно каждому из нас. Например, чтобы прийти вовремя в школу или на работу, приходится измерять время, которое будет потрачено на дорогу. Метеорологи для предсказания погоды измеряют температуру, атмосферное давление, скорость ветра и т. д.

Таблица кубов

К содержанию

Куб числа — есть данное число, возведенное в третью степень. «Кубом» оно называется, потому что такая операция используется для нахождения объема куба (по аналогии с квадратом числа). То есть, чтобы найти объем куба, необходимо возвести в третью степень длину ребра куба. Точно также, чтобы найти куб числа нужно возвести его в третью степень. В таблице приведены значения кубов натуральных чисел от 1 до 100.

1
3
=
1

2
3
=
8

3
3
=
27

4
3
=
64

5
3
=
125

6
3
=
216

7
3
=
343

8
3
=
512

9
3
=
729

10
3
=
1000		 11
3
=
1331

12
3
=
1728

13
3
=
2197

14
3
=
2744

15
3
=
3375

16
3
=
4096

17
3
=
4913

18
3
=
5832

19
3
=
6859

20
3
=
8000		 21
3
=
9261

22
3
=
10648

23
3
=
12167

24
3
=
13824

25
3
=
15625

26
3
=
17576

27
3
=
19683

28
3
=
21952

29
3
=
24389

30
3
=
27000		 31
3
=
29791

32
3
=
32768

33
3
=
35937

34
3
=
39304

35
3
=
42875

36
3
=
46656

37
3
=
50653

38
3
=
54872

39
3
=
59319

40
3
=
64000		 41
3
=
68921

42
3
=
74088

43
3
=
79507

44
3
=
85184

45
3
=
91125

46
3
=
97336

47
3
=
103823

48
3
=
110592

49
3
=
117649

50
3
=
125000
51
3
=
132651

52
3
=
140608

53
3
=
148877

54
3
=
157464

55
3
=
166375

56
3
=
175616

57
3
=
185193

58
3
=
195112

59
3
=
205379

60
3
=
216000		 61
3
=
226981

62
3
=
238328

63
3
=
262144

64
3
=
262144

65
3
=
274625

66
3
=
287496

67
3
=
300763

68
3
=
314432

69
3
=
328509

70
3
=
343000		 71
3
=
357911

72
3
=
373248

73
3
=
389017

74
3
=
405224

75
3
=
421875

76
3
=
438976

77
3
=
456533

78
3
=
474552

79
3
=
493038

80
3
=
512000		 81
3
=
531441

82
3
=
551368

83
3
=
571787

84
3
=
592704

85
3
=
614125

86
3
=
636056

87
3
=
658503

88
3
=
681472

89
3
=
704969

90
3
=
729000		 91
3
=
753571

92
3
=
778688

93
3
=
804357

94
3
=
830584

95
3
=
857375

96
3
=
884736

97
3
=
912673

98
3
=
941192

99
3
=
970299

100
3
=
1000000

Другие заметки по алгебре и геометрии

Полезная информация?

Кубический сантиметр: Космическая мерная чаша

Все мы смотрим на просторы космоса с некоторым удивлением и трепетом. Изучение и понимание космоса требует, чтобы единицы выражали его размер, включая объем. Но из-за этой необъятности мы часто обращаемся к нестандартным метафорам, чтобы передать ее.

Чтобы выразить объем чего-то большого, как, например, Солнце, писатели обычно говорят, что внутри него поместился бы миллион планет Земли. Крошечные объекты требуют таких же творческих аналогий. Вселенная состоит в основном из атомов водорода, масса которых сосредоточена в ядре, обычно в виде одного протона. Этот протон в 1836 раз тяжелее вращающегося вокруг него электрона. Но истинная картина требует, чтобы мы также визуализировали ее структуру, которая в основном представляет собой пустое пространство. Нам бы удалось представить этот протон как изюминку посреди футбольного поля, а электрон — как едва заметную муху на верхней трибуне.

Но аналогии заходят так далеко. Для проведения подробных сравнений нам действительно нужна единая многоцелевая единица объема. Наука выбрала кубический сантиметр (см 3 ).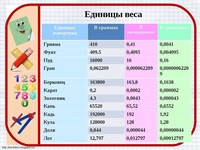 К счастью, есть земной объект именно такого размера: кубик сахара.

В США в 1960-х годах рабочий объем двигателей мотоциклов и автомобилей, который ранее выражался в кубических дюймах, все чаще стали указывать в кубических сантиметрах, сокращенно кубических сантиметрах. Вскоре большинство людей поняли, что такие мотоциклы, как Honda 50, имеют 50-кубовые двигатели, слабые, но дешевые и маневренные. И сегодня большинство американцев знают, что 600-кубовый мотоцикл — это мощная круизная машина, потому что мы привыкли к кубическим сантиметрам. Еще больше упрощая понимание, 1 кубический сантиметр воды весит ровно 1 грамм (тот же вес, что и банкнота в долларах США), поэтому плотность воды составляет 1 г/см 9 .0007 3 .

Это позволяет легко представить общую плотность Земли в 5,5 г/см 3 , что является самой высокой плотностью среди всех планет Солнечной системы. И зная, что плотность Сатурна составляет 0,7 г/см 3 , можно предположить, что он состоит из легких элементов, таких как гелий, и объясняет, почему он плавает на воде.

На самом деле, когда мы используем кубические сантиметры, возникают всевозможные откровения. Мы уже видели, что каждый атом в основном представляет собой пустое пространство, поэтому вполне логично, что в нашей жизни или в наших телах очень мало реального материала. Если мы возьмем всю человеческую расу, насчитывающую около 8 миллиардов человек, и удалим все пустые пространства внутри и между нашими атомами, одна только наша материя — по сути, объединенные атомные ядра всех — уместится в одном кусочке сахара. Правильно, весь наш вид составляет 1 кубический сантиметр твердого материала после того, как вы удалили пустые места. Плюх! Налейте нас в чашку чая.

Но мы здесь, чтобы расширить наши умы в основном неизвестными идеями, и вы, возможно, слышали об этом. Итак, как вам второй факт: яркость космоса, по сути, сводится к тому, сколько фотонов он содержит. Вселенная без фотонов была бы кромешной тьмой. Что ж, в космосе на каждый протон приходится миллиард фотонов. Но что это значит, учитывая огромное пустое пространство? Более полезным ответом будет то, что в среднем в нашем космосе 413 фотонов на кубический сантиметр! Вот почему мы видим красивые вещи в наши телескопы.

Наконец, поскольку мы любим превосходную степень, какую максимальную плотность мы можем выразить в кубических сантиметрах? Не плотность черной дыры, поскольку сама сингулярность может достигать бесконечной плотности, хотя многие физики возражают, что бесконечная плотность — это концепция, лишенная какого-либо физического смысла в реальном мире. Но нейтронные звезды разные. Это, как и Крабовидный пульсар, объекты со стабильной плотностью. Итак, какая плотность у нейтронной звезды? Ответ: 100 трлн г/см 3 . Это эквивалентно одному кубику сахара весом в сто миллионов тонн — кубику сахара, равному массе 640 круизных лайнеров.

Все еще думаете, что это не странная вселенная?

Преобразование кубических футов в кубические сантиметры (ft³ в cm³)

Кубический фут и кубический сантиметр — это единицы измерения объема. Объем трехмерного объекта или формы называется заключенным в них пространством. Например, предположим, что емкость кубической формы заполнена песком. Чтобы найти количество песка, засыпанного в контейнер, нам нужно рассчитать объем контейнера. Объем любого трехмерного объекта измеряется в кубических единицах. В зависимости от заданных единиц это может быть выражено как m 3 , cm 3 , in 3 , ft 3 и т. д. Однако кубический метр (m 3 ) считается единицей объема в системе СИ.

Кубический фут — единица измерения объема куба, длина каждой стороны которого равна одному футу. Это единица измерения объема, которая в основном используется в традиционной и имперской системах измерения Соединенных Штатов и символически представлена ​​​​как ft 3 . Мы можем записать 1 кубический фут как 1 куб. футов или 1 фут 3 , емкость которого составляет около 28,3168 л. Объем кубического фута в галлонах определяется как 1 кубический фут, эквивалентный 7,48052 жидких галлонов США.

Кубический сантиметр — единица измерения объема куба, длина каждой стороны которого равна одному сантиметру. Это единица измерения единичного объема, которая обычно используется для измерения меньших объемов и символически обозначается как см 3 . Мы можем записать 1 кубический сантиметр как 1 куб. см. или 1 см 3

Как преобразовать кубический фут в кубический сантиметр?

Значение 1 кубического фута приблизительно равно 28316,85 кубических сантиметров . Итак, чтобы преобразовать кубические футы в кубические метры, мы должны умножить данное значение фута на 28316,85 кубических сантиметра.

Например,

Чтобы преобразовать 15 кубических футов в кубические сантиметры, умножьте 15 на 28316,85 кубических сантиметра, т. е.

15 кубических футов = 15 × 28316,85 кубических сантиметра

15 кубических футов = 42475,275 кубических сантиметра.

Следовательно, 15 кубических футов приблизительно равны 42475,275 кубических сантиметра.

Таблица преобразования

Перевод кубических футов в кубические метры для определенных значений приведен ниже:

900 85

2

 кубический фут (футы 3 )

Кубический сантиметр

(см 3 )

0,01

283,1685

0,1

90 096

2831. 685

1

28316.85

56633.7

3

84950.55

4 9000 3

113267.4

5

141584.25

10

28316 8.5

20

566337

50

9009 6

1415842.5

100

283168,5

Примеры вопросов футов и кубических сантиметров.

Решение:

Кубические метры и кубические футы — единицы объема трехмерного объекта.

1 кубический фут ≈ 28316,85 кубических сантиметра

(или)

1 кубический сантиметр = 0,00003531466247 кубических футов.

Вопрос 2: Переведите 5 кубических футов в кубические сантиметры.

Решение:

Мы знаем, что

1 кубический фут ≈ 28316,85 кубических сантиметра.

Следовательно,

5 кубических футов = 5 × 28316,85 кубических сантиметров

5 футов 3 = 141584,25 см 3 .

Следовательно, 5 кубических футов примерно равны 141584,25 кубических сантиметра.

Вопрос 3: Переведите 0,73 кубических фута в кубические сантиметры.

Решение:

Мы знаем, что

1 кубический фут ≈ 28316,85 кубических сантиметра.

Следовательно,

0,73 фута 3  = 0,73 × 28316,85 см 3

0,73 фута 3 = 20671,3005 см 3 .

Таким образом, 0,73 кубических фута примерно равны 0,0206713005 кубических сантиметров.

Вопрос 4: Переведите 35 кубических футов в кубические сантиметры.

Решение:

Мы знаем, что

1 кубический фут ≈ 28316,85 кубических сантиметра.

Следовательно,

35 футов 3  = 35 × 28316,85 см 3

35 футов 3 = 991089,75 см 3 .

Таким образом, 35 ​​кубических футов примерно равны 991089,75 кубических сантиметров.

Вопрос 5: Найдите объем комнаты, имеющей размеры 6 футов × 8 футов × 10 футов, и переведите кубические футы в кубические сантиметры.

Решение:

Дано,

Размеры комнаты 6 футов, 8 футов и 10 футов.

Теперь объем комнаты (V) = l × b × h

В = 6×8×10 = 480 куб. футов

Мы знаем, что

1 кубический фут ≈ 28316,85 кубических сантиметра.

Следовательно,

480 футов 3  = 480 × 28316,85 см 3

480 футов 3 = 13592088 см 3 .

Таким образом, 480 кубических футов примерно равны 13592088 кубических сантиметров.

Вопрос 6: Переведите 128 кубических футов в кубические сантиметры.

Posted inКоробка передач