Содержание
Коэффициент полезного действия (кпд) — формулы, обозначение, расчет
КПД: понятие коэффициента полезного действия
Представьте, что вы пришли на работу в офис, выпили кофе, поболтали с коллегами, посмотрели в окно, пообедали, еще посмотрели в окно — вот и день прошел. Если вы не сделали ни одного дела по работе, то можно считать, что ваш коэффициент полезного действия равен нулю.
В обратной ситуации, когда вы сделали все запланированное — КПД равен 100%.
По сути, КПД — это процент полезной работы от работы затраченной.
Вычисляется по формуле:
Формула КПД η = (Aполезная/Aзатраченная) · 100% η — коэффициент полезного действия [%] Aполезная — полезная работа [Дж] Aзатраченная — затраченная работа [Дж] |
Есть такое философское эссе Альбера Камю «Миф о Сизифе». Оно основано на легенде о неком Сизифе, который был наказан за обман. Его приговорили после смерти вечно таскать огромный булыжник вверх на гору, откуда этот булыжник скатывался, после чего Сизиф тащил его обратно в гору. То есть он делал совершенно бесполезное дело с нулевым КПД. Есть даже выражение «Сизифов труд», которое описывает какое-либо бесполезное действие.
Оно основано на легенде о неком Сизифе, который был наказан за обман. Его приговорили после смерти вечно таскать огромный булыжник вверх на гору, откуда этот булыжник скатывался, после чего Сизиф тащил его обратно в гору. То есть он делал совершенно бесполезное дело с нулевым КПД. Есть даже выражение «Сизифов труд», которое описывает какое-либо бесполезное действие.
Давайте пофантазируем и представим, что Сизифа помиловали и камень с горы не скатился. Тогда, во-первых, Камю бы не написал об этом эссе, потому что никакого бесполезного труда не было. А во-вторых, КПД в таком случае был бы не нулевым.
Полезная работа в этом случае равна приобретенной булыжником потенциальной энергии. Потенциальная энергия прямо пропорционально зависит от высоты: чем выше расположено тело, тем больше его потенциальная энергия. То есть, чем выше Сизиф прикатил камень, тем больше потенциальная энергия, а значит и полезная работа.
Потенциальная энергия Еп = mg Еп — потенциальная энергия [Дж] m — масса тела [кг] g — ускорение свободного падения [м/с2] h — высота [м] На планете Земля g ≃ 9,8 м/с2 |
Затраченная работа здесь — это механическая работа Сизифа.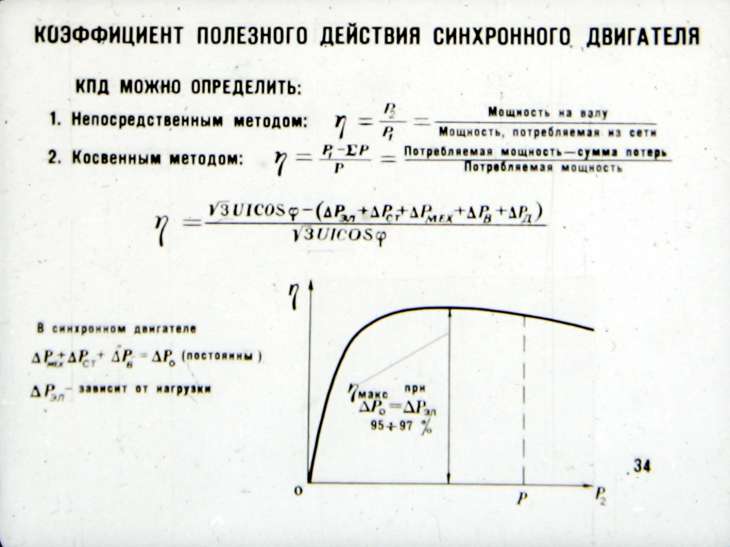 Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.
Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.
Механическая работа А = FS A — механическая работа [Дж] F — приложенная сила [Н] S — путь [м] |
И как же достоверно определить, какая работа полезная, а какая затраченная? Все очень просто! Задаем два вопроса:
В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы). |
Не отбрасываем!
Если КПД получился больше 100 — идем проверять на ошибки. Такое может получиться, если неправильно подставили в формулу или перепутали затраченную и полезную работу.
η = (Aполезная/Aзатраченная) · 100% η — коэффициент полезного действия [%] Aполезная — полезная работа [Дж] Aзатраченная — затраченная работа [Дж] |
Дальше мы просто заменяем полезную и затраченную работы на те величины, которые ими являются.
Давайте разберемся на примере задачи.
Задача
Чтобы вкатить санки массой 4 кг в горку длиной 12 метров, мальчик приложил силу в 15 Н. Высота горки равна 2 м. Найти КПД этого процесса. Ускорение свободного падения принять равным g ≃9,8 м/с2
Высота горки равна 2 м. Найти КПД этого процесса. Ускорение свободного падения принять равным g ≃9,8 м/с2
Запишем формулу КПД.
η = (Aполезная/Aзатраченная) · 100%
Теперь задаем два главных вопроса:
Ради чего все это затеяли?
Чтобы санки в горку поднять — то есть ради приобретения телом потенциальной энергии. Значит в данном процессе полезная работа равна потенциальной энергии санок.
Потенциальная энергия Еп = mg Еп — потенциальная энергия [Дж] m — масса тела [кг] g — ускорение свободного падения [м/с2] h — высота [м] На планете Земля g ≃ 9,8 м/с2 |
За счет чего процесс происходит?
За счет мальчика, он же тянет санки.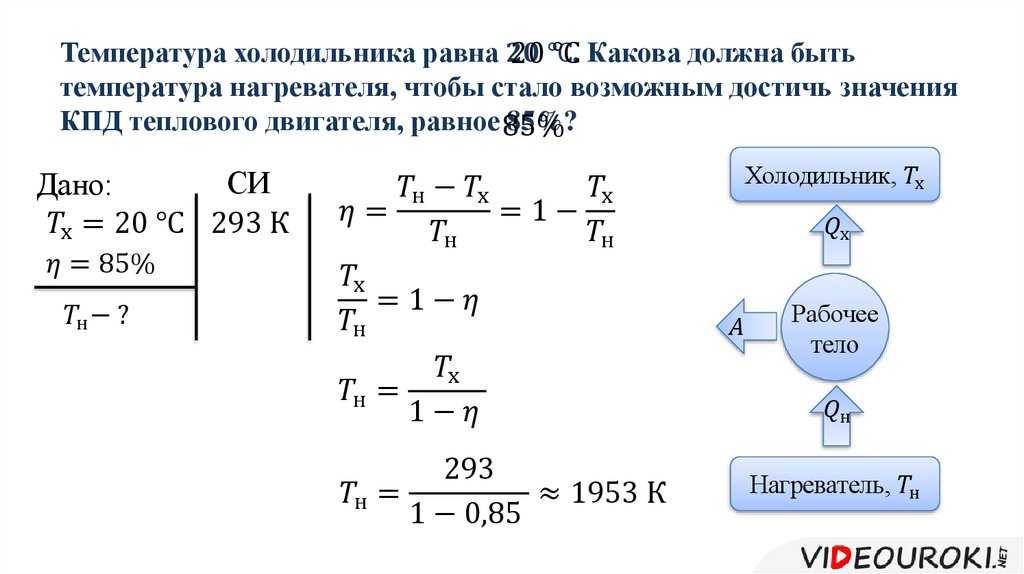 Значит затраченная работа равна механической работе
Значит затраченная работа равна механической работе
Механическая работа А = FS A — механическая работа [Дж] F — приложенная сила [Н] S — путь [м] |
Заменим формуле КПД полезную работу на потенциальную энергию, а затраченную — на механическую работу:
η = Eп/A · 100% = mgh/FS · 100%
Подставим значения:
η = 4 · 9,8 · 2/15 · 12 · 100% = 78,4/180 · 100% ≃ 43,6 %
Ответ: КПД процесса приблизительно равен 43,6%
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
КПД в термодинамике
В термодинамике КПД — очень важная величина. Она полностью определяет эффективность такой штуки, как тепловая машина.
- Тепловой двигатель (машина) — это устройство, которое совершает механическую работу циклически за счет энергии, поступающей к нему в ходе теплопередачи.

Схема теплового двигателя выглядит так:
У теплового двигателя обязательно есть нагреватель, который (не может быть!) нагревает рабочее тело, передавая ему количество теплоты Q1 или Qнагревателя (оба варианта верны, это зависит лишь от учебника, в котором вы нашли формулу).
- Рабочее тело — это тело, на котором завязан процесс (чаще всего это газ или топливо). Оно расширяется при подводе к нему теплоты и сжимается при охлаждении. Часть переданного Q1 уходит на механическую работу A. Из-за этого производится движение.
Оставшееся количество теплоты Q2 или Qхолодильника отводится к холодильнику, после чего возвращается к нагревателю и процесс повторяется.
КПД такой тепловой машины будет равен:
КПД тепловой машины η = (Aполезная/Qнагревателя) · 100% η — коэффициент полезного действия [%] Aполезная — полезная работа (механическая) [Дж] Qнагревателя — количество теплоты, полученное от нагревателя[Дж] |
Если мы выразим полезную (механическую) работу через Qнагревателя и Qхолодильника, мы получим:
A = Qнагревателя — Qхолодильника.
Подставим в числитель и получим такой вариант формулы.
КПД тепловой машины η = Qнагревателя − Qхолодильника/Qнагревателя · 100% η — коэффициент полезного действия [%] Qнагревателя — количество теплоты, полученное от нагревателя [Дж] Qхолодильника — количество теплоты, отданное холодильнику [Дж] |
А возможно ли создать тепловую машину, которая будет работать только за счет охлаждения одного тела?
Точно нет! Если у нас не будет нагревателя, то просто нечего будет передавать на механическую работу. Любой такой процесс — когда энергия не приходит из ниоткуда — означал бы возможность существования вечного двигателя.
Поскольку свидетельств такого процесса в мире не существует, то мы можем сделать вывод: вечный двигатель невозможен. Это второе начало термодинамики.
Это второе начало термодинамики.
Запишем его, чтобы не забыть:
Невозможно создать периодическую тепловую машину за счет охлаждения одного тела без изменений в других телах.
Задача
Найти КПД тепловой машины, если рабочее тело получило от нагревателя 20кДж, а отдало холодильнику 10 кДж.
Решение:
Возьмем формулу для расчета КПД:
η = Qнагревателя − Qхолодильника/Qнагревателя · 100%
Решать будем в системе СИ, поэтому переведем значения из килоджоулей в джоули и затем подставим в формулу:
η = 20 000 − 10 000/20 000 · 100% = 50%
Ответ: КПД тепловой машины равен 50%.
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Идеальная тепловая машина: цикл Карно
Давайте еще чуть-чуть пофантазируем: какая она — идеальная тепловая машина. Кажется, что это та, у которой КПД равен 100%.
Кажется, что это та, у которой КПД равен 100%.
На самом деле понятие «идеальная тепловая машина» уже существует. Это тепловая машина, у которой в качестве рабочего тела взят идеальный газ. Такая тепловая машина работает по циклу Карно. Зависимость давления от объема в этом цикле выглядит следующим образом
А КПД для цикла Карно можно найти через температуры нагревателя и холодильника.
КПД цикла Карно η = Tнагревателя − Tхолодильника / Tнагревателя · 100% η — коэффициент полезного действия [%] Tнагревателя — температура нагревателя [Дж] Tхолодильника — температура холодильника [Дж] |
КПД в электродинамике
Мы каждый день пользуемся различными электронными устройствами: от чайника до смартфона, от компьютера до робота-пылесоса — и у каждого устройства можно определить, насколько оно эффективно выполняет задачу, для которой оно предназначено, просто посчитав КПД.
Вспомним формулу:
КПД η = (Aполезная/Aзатраченная) · 100% η — коэффициент полезного действия [%] Aполезная — полезная работа [Дж] Aзатраченная — затраченная работа [Дж] |
Для электрических цепей тоже есть нюансы. Давайте разбираться на примере задачи.
Задачка, чтобы разобраться
Найти КПД электрического чайника, если вода в нем приобрела 22176 Дж тепла за 2 минуты, напряжение в сети — 220 В, а сила тока в чайнике 1,4 А.
Решение:
Цель электрического чайника — вскипятить воду. То есть его полезная работа — это количество теплоты, которое пошло на нагревание воды. Оно нам известно, но формулу вспомнить все равно полезно 😉
Оно нам известно, но формулу вспомнить все равно полезно 😉
Количество теплоты, затраченное на нагревание Q = cm(tконечная − tначальная) Q — количество теплоты [Дж] c — удельная теплоемкость вещества [Дж/кг · ˚C] m — масса [кг] tконечная — конечная температура [˚C] tначальная — начальная температура [˚C] |
Работает чайник, потому что в розетку подключен. Затраченная работа в данном случае — это работа электрического тока.
Работа электрического тока A = (I2) · Rt = (U2)/R · t = UIt A — работа электрического тока [Дж] I — сила тока [А] U — напряжение [В] R — сопротивление [Ом] t — время [c] |
То есть в данном случае формула КПД будет иметь вид:
η = Q/A · 100% = Q/UIt · 100%
Переводим минуты в секунды — 2 минуты = 120 секунд. Теперь нам известны все значения, поэтому подставим их:
Теперь нам известны все значения, поэтому подставим их:
η = 22176/220 · 1,4 · 120 · 100% = 60%
Ответ: КПД чайника равен 60%.
Давайте выведем еще одну формулу для КПД, которая часто пригождается для электрических цепей, но применима ко всему. Для этого нужна формула работы через мощность:
Работа электрического тока A = Pt A — работа электрического тока [Дж] P — мощность [Вт] t — время [c] |
Подставим эту формулу в числитель и в знаменатель, учитывая, что мощность разная — полезная и затраченная. Поскольку мы всегда говорим об одном процессе, то есть полезная и затраченная работа ограничены одним и тем же промежутком времени, можно сократить время и получить формулу КПД через мощность.
КПД η = Pполезная/Pзатраченная · 100% η — коэффициент полезного действия [%] Pполезная — полезная мощность [Дж] Pзатраченная — затраченная мощность [Дж] |
Как определить кпд генератора и двигателя
Содержание
- Коэффициент полезного действия
- Потери энергии и коэффициент полезного действия генераторов постоянного тока
- КПД электродвигателей
- Подписка на рассылку
- Определение КПД электродвигателя
- Факторы, влияющие на величину КПД
- Способы повысить КПД двигателя
- Понятие КПД электродвигателя
- Что такое КПД электродвигателя и его простейшая формула
- Величины КПД современных электродвигателей
- Факторы, влияющие на изменение КПД электрической машины
- Может ли КПД быть более 100%?
- Коэффициент полезного действия машины постоянного тока
- Общие положения
- Прямой и косвенный методы определения коэффициента полезного действия
- Условия максимума коэффициента полезного действия
- Видео
Коэффициент полезного действия
Зная потери в машине, можно определить коэффициент полезного действия (к. п. д.) машины.
п. д.) машины.
а) Коэффициент полезного действия генератора постоянного тока.
Для генераторов к. п. д. представляет собой отношение электрической полезной мощности к механической мощности на валу и определяется по формуле:
Механическую мощность на валу генератора можно представить как:
Электрическая полезная мощность генератора определяется по формуле:
где: ∑P — сумма всех потерь в машине;
Тогда для генератора коэффициент полезного действия можно определить по формулам:
б) Коэффициент полезного действия двигателя постоянного тока.
Коэффициентом полезного действия двигателя постоянного тока называется отношение механической мощности на валу двигателя Р2 к подводимой к двигателю электрической мощности Р1.
В двигателях подводимая мощность Р1 определяется по формуле:
Механическую мощность на валу двигателя можно представить как:
где: ∑P — сумма всех потерь в машине;
Тогда для двигателя коэффициент полезного действия можно определить по формулам:
При х. х. машин, когда полезная мощность равна нулю, к. п. д. = 0.
х. машин, когда полезная мощность равна нулю, к. п. д. = 0.
По мере увеличения нагрузки к. п. д. машины быстро увеличивается.
Наибольшее значение он имеет при нагрузке, равной (0,8-1) Рном когда постоянные потери равны переменным.
При значительных перегрузках вследствие увеличения потерь в сопротивлениях цепи якоря к. п. д. снова снижается.
Рис.20.1. Зависимость к.п.д. машины от нагрузки
Современные электрические машины имеют высокий к. п. д.
Так, для машин постоянного тока:
мощностью 10 кВт к. п. д. η = 0,83- 0,87;
мощностью 100 кВт; η =0,884-0,93;
мощностью 1000 кВт η = 0,92-0,96.
Машины малой мощности имеют меньшее значение к. п. д., например для двигателя мощностью 10 Вт η = 0,34-0,4
Дата добавления: 2014-12-24 ; просмотров: 1906 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
Потери энергии и коэффициент полезного действия генераторов постоянного тока
Любой процесс преобразования энергии из одного вида в другой сопровождается необратимыми потерями энергии, которые в конечном счете обращаются в тепло и рассеиваются в окружающую среду.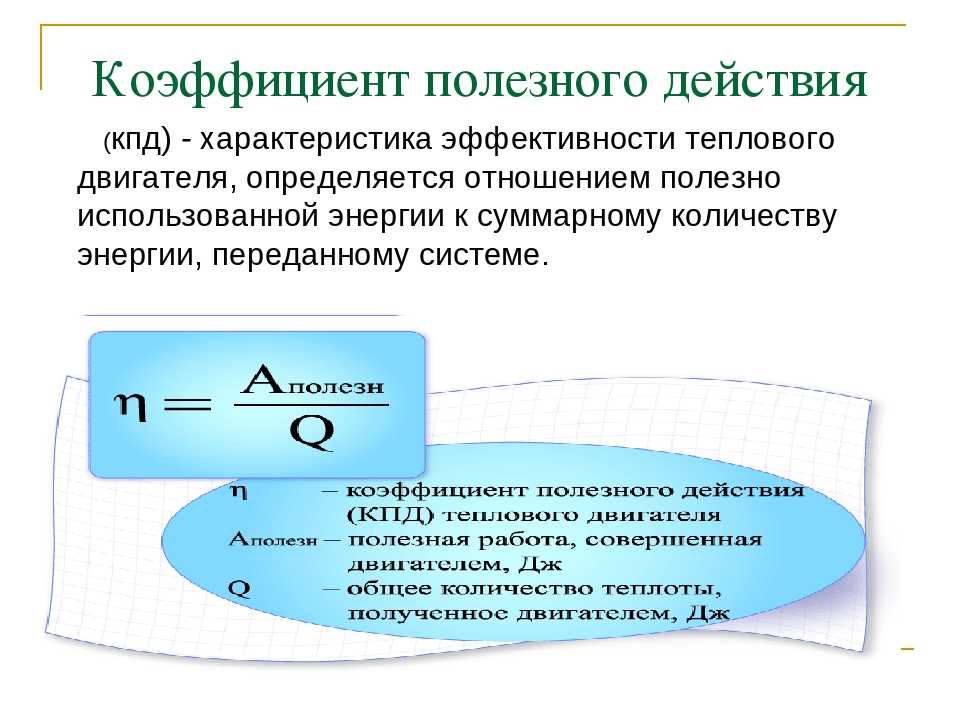
В генераторах постоянного тока различают следующие виды потерь:
Механические потери и потери в стали не зависят от нагрузки генератора. Потери в меди и щеточном контакте существенно изменяются при изменении нагрузки.
На энергетической диаграмме генератора (рис. 7.27) наглядно представ- лены различные виды потерь.
Коэффициентом полезного действия генератора (КПД) называют отношение электрической мощности Р2, отдаваемой генератором в сеть, к механической мощности Д, развиваемой приводным двигателем на валу генератора:
Подсчет КПД по этой формуле приводит к очень неточным результатам, так как погрешности измерения относительно высоких мощностей Д и Р2 выражаются в больших абсолютных цифрах.
Более точный результат дает формула, в которой потери выражены в явном виде:
Сумма (Ржк + Ра) составляет потери холостого хода и равна мощности, потребляемой генератором в режиме холостого хода за вычетом мощности, расходуемой в цепи возбуждения.
КПД генератора зависит от нагрузки (рис. 7.28). В частности, в режиме холостого хода КПД генератора равен нулю.
Генераторы рассчитывают таким образом, чтобы максимальный КПД достигался при значениях тока, близких к номинальному. Величина КПД генераторов постоянного тока мощностью до 100 кВт при номинальной нагрузке составляет 75—92%.
Чем больше мощность машины, тем выше ее КПД.
Потери энергии и коэффициент полезного действия генераторов постоянного тока
Какие виды потерь энергии существуют в генераторах постоянного тока?
Потери на трение, потери в стали
Потери в обмотках якоря и возбуждения
Потери в щеточных контактах, добавочные потери
Все виды потерь, перечисленные выше
Продолжение карт. №7.12
При увеличении скоро- сти вращения якоря в 2 раза как изменятся:
Как изменятся потери в обмотке якоря при увеличении нагрузки генератора в 2 раза?
Увеличатся в 2 раза
Увеличатся в 4 раза
Мощность, потребля- емая генератором от приводного двигателя, 50 кВт. Мощность, отдаваемая в сеть, 45 кВт. Определите КПД генератора, %.
Мощность, отдаваемая в сеть, 45 кВт. Определите КПД генератора, %.
Генератор отдает в сеть мощность 8 кВт. Суммарные потери мощ- ности в генераторе 2 кВт. Определите КПД генератора, %
Источник
КПД электродвигателей
Подписка на рассылку
Электрическими двигателями переменного или постоянного тока комплектуются приводы станков, насосов и вентиляторов, а также других механизмов, используемых на предприятиях тяжелой и легкой промышленности. Рентабельность производства напрямую зависит от себестоимости продукции, на которую в большой степени влияет эффективность эксплуатации оборудования, поэтому КПД и мощность электродвигателя являются основными параметрами, на основании которых выполняется подбор привода.
Определение КПД электродвигателя
Принцип работы любой электрической машины основан на преобразовании энергии тока, протекающего по обмоткам статора и создающего магнитное поле, во вращение ротора. Коэффициент полезного действия (КПД) электродвигателя определяется соотношением вырабатываемой им механической мощности на валу (p2) к полной мощности, потребляемой из сети (p1) и выражается в процентах:
Исходя из формулы, следует, что чем ближе этот параметр к единице, тем выше будет эффективность использования оборудования.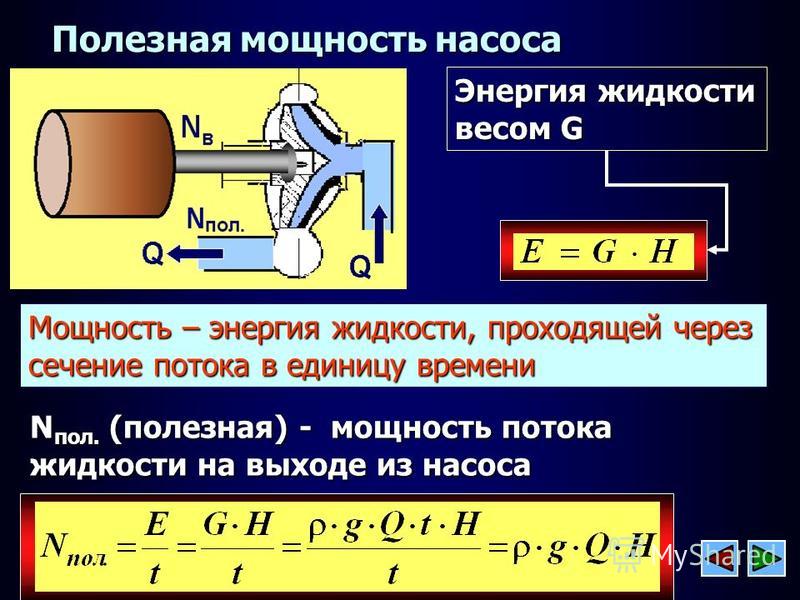
Факторы, влияющие на величину КПД
Коэффициент полезного действия никогда не может быть равным единице, так как существуют неизбежные потери, снижающие полезную мощность. Они делятся на три группы:
Электрические потери зависят от степени нагрузки двигателя и являются следствием нагрева обмоток статора, вызванного работой тока по преодолению электрического сопротивления проводников, из которых они выполнены. Поэтому максимальный КПД электродвигателя достигается, когда нагрузка на двигатель составляет 75% от максимальной расчетной величины.
Магнитные потери происходят из-за неизбежного перемагничивания активного железа статора и ротора, а также возникновения в нем вихревых токов.
Третья группа обусловлена наличием трения в подшипниках, на которых вращается вал, а также сопротивлением, оказываемым воздухом крыльчатке вентилятора и самому ротору (якорю). Из-за наличия щеточно-коллекторного узла КПД электродвигателя постоянного тока несколько ниже коэффициента полезного действия машин с короткозамкнутым ротором. Это также относится к асинхронным электродвигателям с фазным ротором из-за дополнительного трения щеток об контактные кольца.
Это также относится к асинхронным электродвигателям с фазным ротором из-за дополнительного трения щеток об контактные кольца.
Способы повысить КПД двигателя
Следует помнить, что реальный коэффициент полезного действия может несколько отличатся от паспортных величин, указанных на шильдике двигателя. Чтобы выполнить расчет КПД электродвигателя в реальных условиях эксплуатации, необходимо учитывать неравномерность распределения питающего напряжения в фазах. В зависимости от величины асимметрии падение полезной мощности может достигать 5-7%.
Увеличение КПД электрической машины возможно только за счет снижения потерь и контроля качества силовой сети.
Механические потери можно уменьшить благодаря более качественным подшипникам, установки крыльчатки вентилятора, выполненной из современных материалов для уменьшения сопротивлению воздуху. Нагрев обмоток можно уменьшить благодаря использованию обмоточных проводов, выполненных из очищенной меди, имеющих меньшее сопротивление.
Снизить потери на перемагничивание активного железа и минимизировать влияние вихревых токов можно используя для набора сердечника необходимо использовать качественную электромагнитную сталь с надежной изоляцией. Кроме того, ведутся работы по разработке наилучшей геометрии зубцов статора, благодаря которым будет увеличена концентрация магнитного поля.
В реальности КПД асинхронного электродвигателя можно несколько увеличить за счет использования частотного преобразователя, позволяющего оптимизировать расход электроэнергии. Следует помнить, что эффективность эксплуатации двигателя с КПД 98% сильно упадет, если его использовать для приведения в движения механизма, имеющего более низкий коэффициент полезного действия.
Источник
Понятие КПД электродвигателя
Что такое КПД электродвигателя и его простейшая формула
Эффективность работы любого электропривода, в первую очередь, определяется коэффициентом полезного действия электродвигателя (КПД). Говоря простым языком, электрическая машина, потребляя электрическую энергию, преобразует её в механическую для работы различных устройств, станков, инструментов и проч. Соотношение величин полезной механической мощности на валу двигателя (Р 2 ) к мощности, потребляемой из сети (Р 1 ), и есть КПД (η). КПД является номинальной величиной и указывается в процентах: η = (Р 2 / Р 1 ) х 100%.
Говоря простым языком, электрическая машина, потребляя электрическую энергию, преобразует её в механическую для работы различных устройств, станков, инструментов и проч. Соотношение величин полезной механической мощности на валу двигателя (Р 2 ) к мощности, потребляемой из сети (Р 1 ), и есть КПД (η). КПД является номинальной величиной и указывается в процентах: η = (Р 2 / Р 1 ) х 100%.
Важность такого показателя как КПД обусловлена прежде всего тем, что около 70% вырабатываемой во всём мире электроэнергии потребляется электродвигателями, начиная от простейших бытовых электроприборов до вентиляционных установок и приводов оборудования крупнейших предприятий.
Величины КПД современных электродвигателей
У большинства современных электродвигателей КПД лежит в пределах 80-90%. Нередко встречаются маломощные модели с КПД до 75%.
Для машин, работающих в особых условиях, современные технологии позволяют увеличивать КПД до 96%. Это достигается не только за счёт их высокоточного производства, но и благодаря использованию дорогостоящих материалов для сердечников, перемагничивание которых не сопряжено с высокими энергетическими затратами.
Факторы, влияющие на изменение КПД электрической машины
Сразу следует сделать уточнение: КПД электропривода никогда не превышает 100%.
Это объясняется расходом потребляемой мощности на нагрев обмоток двигателя, перемагничивание статора (в асинхронных двигателях), вихревые токи, механическое сопротивление при движении ротора.
Нагрев обмоток двигателя – явление закономерное. Из курса физики известно:
Если с первым пунктом всё ясно, то пункт 2 требует дополнительных объяснений. Традиционно внимание акцентируется на том, что пропитка обмоток статора делается для их защиты от влияния влаги или агрессивной среды. Но также следует учитывать, что после пропитки не остаётся свободных зазоров между обмоткой и сердечником статора, а это позволяет значительно увеличить теплоотдачу и снизить нагрев во время работы. Для этой же цели предусмотрена такая конструктивная особенность как монолитная отливка корпуса с охлаждающими рёбрами, что в значительной мере стабилизирует рабочий нагрев электропривода и препятствует снижению КПД.
Расчётная температура нагрева для двигателей класса “А” лежит в пределах 90℃, для класса “В” не превышает 110℃.
Вихревые токи или токи Фуко (иногда можно встретить термин “паразитарные токи”) возникают в металлических элементах там, где есть переменное магнитное поле. Согласно закону Ленца они являются причиной наведения магнитных потоков, противодействующих рабочему магнитному потоку вокруг катушек. Понятно, что это влияет на крутящий момент и вызывает дополнительный нагрев двигателя, снижая КПД.
Для уменьшения потерь от вихревых токов надо увеличить электрическое сопротивление магнитопровода. Поэтому магнитопроводы и сердечники якорей набирают (шихтуют) из очень тонких (до 0,5 мм) пластин электротехнической стали, иногда с добавлением кремния, покрытых специальным лаком для их изоляции друг от друга. До сих пор существуют производственные участки, где для этой цели применяют тяжёлый ручной труд.
Механические факторы снижения КПД электродвигателя возникают в результате конструктивных изменений, трения в подшипниках, воздушного сопротивления
Нередко в процессе эксплуатации наблюдаются искривление вала и другие дефекты, вызывающие вибрации на опорных подшипниках ротора, и, соответственно, увеличение механического сопротивления.
Бывает так, что в случае заводского брака при изготовлении обмоток (несоблюдении расчётного количества витков одной из обмоток) нарушается плавность хода ротора, что тоже сказывается на эффективности работы электродвигателя. (Утверждение, что опытный электромеханик определяет эту неполадку на слух, является правдой.)
Может ли КПД быть более 100%?
Если говорить об электродвигателях, то следует однозначно заявить: нет!
Выше уже отмечалось, что в электрических машинах мы сталкиваемся с энергией магнитного поля, электрической энергией, тепловой и механической. Достаточно минимальных знаний из области физики и основ электротехники, чтобы раз и навсегда усвоить: преобразованию одного вида энергии в другой всегда сопутствуют процессы обратной направленности. Для примера можно вспомнить токи Фуко.
Существует ещё один важный аргумент в пользу утверждения о невозможности достижения КПД свыше 100%. На данном этапе развития человечество не обладает технологиями производства универсальных материалов, которые не нагревались бы в процессе работы или демонстрировали молниеносное перемагничивание, а также не подвергались бы механической усталости.
Многочисленные энтузиасты не оставляют попыток создать устройства, которые могли бы, выполнять механическую работу и одновременно вырабатывать электроэнергию, покрывая потери и собственные энергозатраты. При этом они не учитывают элементарный принцип обратимости электрических машин: либо генератор, либо двигатель.
Источник
Коэффициент полезного действия машины постоянного тока
Общие положения
Коэффициент полезного действия определяется как отношение полезной, или отдаваемой, мощности P2 к потребляемой мощности P1:
Современные электрические машины имеют высокий коэффициент полезного действия (к. п. д.). Так, у машин постоянного тока мощностью 10 кВт к. п. д. составляет 83 – 87%, мощностью 100 кВт – 88 – 93% и мощностью 1000 кВт – 92 – 96%. Лишь малые машины имеют относительно низкие к. п. д.; например, у двигателя постоянного тока мощностью 10 Вт к. п. д. 30 – 40%.
Рисунок 1. Зависимость коэффициента полезного действия электрической машины от нагрузки Зависимость коэффициента полезного действия электрической машины от нагрузки |
Кривая к. п. д. электрической машины η = f(P2) сначала быстро растет с увеличением нагрузки, затем к. п. д. достигает максимального значения (обычно при нагрузке, близкой к номинальной) и при больших нагрузках уменьшается (рисунок 1). Последнее объясняется тем, что отдельные виды потерь (электрические Iа 2 rа и добавочные) растут быстрее, чем полезная мощность.
Прямой и косвенный методы определения коэффициента полезного действия
Прямой метод определения к. п. д. по экспериментальным значениям P1 и P2 согласно формуле (1) может дать существенную неточность, поскольку, во-первых, P1 и P2 являются близкими по значению и, во-вторых, их экспериментальное определение связано с погрешностями. Наибольшие трудности и погрешности вызывает измерение механической мощности.
Если, например, истинные значения мощности P1 = 1000 кВт и P2 = 950 кВт могут быть определены с точностью 2%, то вместо истинного значения к. п. д.
Поэтому ГОСТ 25941-83, «Машины электрические вращающиеся. Методы определения потерь и коэффициента полезного действия», предписывает для машин с η% ≥ 85% косвенный метод определения к. п. д., при котором по экспериментальным данным определяется сумма потерь pΣ.
Применив здесь подстановку P1 = P2 + pΣ, получим другой вид формулы:
Так как более удобно и точно можно измерять электрические мощности (для двигателей P1 и для генераторов P2), то для двигателей более подходящей является формула (3) и для генераторов формула (4). Методы экспериментального определения отдельных потерь и суммы потерь pΣ описываются в стандартах на электрические машины и в руководствах по испытанию и исследованию электрических машин. Если даже pΣ определяется со значительно меньшей точностью, чем P1 или P2, при использовании вместо выражения (1) формул (3) и (4) получаются все же значительно более точные результаты.
Если даже pΣ определяется со значительно меньшей точностью, чем P1 или P2, при использовании вместо выражения (1) формул (3) и (4) получаются все же значительно более точные результаты.
Условия максимума коэффициента полезного действия
Различные виды потерь различным образом зависят от нагрузки. Обычно можно считать, что одни виды потерь остаются постоянными при изменении нагрузки, а другие являются переменными. Например, если генератор постоянного тока работает с постоянной скоростью вращения и постоянным потоком возбуждения, то механические и магнитные потери являются также постоянными. Наоборот, электрические потери в обмотках якоря, добавочных полюсов и компенсационной изменяются пропорционально Iа², а в щеточных контактах – пропорционально Iа. Напряжение генератора при этом также приблизительно постоянно, и поэтому с определенной степенью точности P2 ∼ Iа.
Таким образом, в общем, несколько идеализированном случае можно положить, что
где коэффициент нагрузки
Определяет относительную величину нагрузки машины.
Суммарные потери также можно выразить через kнг:
где p0 – постоянные потери, не зависящие от нагрузки; p1 – значение потерь, зависящих от первой степени kнг при номинальной нагрузке; p2 – значение потерь, зависящих от квадрата kнг, при номинальной нагрузке.
Подставим P2 из (5) и pΣ из (7) в формулу к. п. д.
Установим, при каком значении kнг к. п. д. достигает максимального значения, для чего определим производную dη/dkнг по формуле (8) и приравняем ее к нулю:
Это уравнение удовлетворяется, когда его знаменатель равен бесконечности, т. е. при kнг = ∞. Этот случай не представляет интереса. Поэтому необходимо положить равным нулю числитель. При этом получим
Поэтому необходимо положить равным нулю числитель. При этом получим
Таким образом, к. п. д. будет максимальным при такой нагрузке, при которой переменные потери kнг² × p2, зависящие от квадрата нагрузки, становятся равными постоянным потерям p0.
Значение коэффициента нагрузки при максимуме к. п. д., согласно формуле (9),
Если машина проектируется для заданного значения ηмакс, то, поскольку потери kнг × p1 обычно относительно малы, можно считать, что
Изменяя при этом соотношение потерь p0 и p2, можно достичь максимального значения к. п. д. при различных нагрузках. Если машина работает большей частью при нагрузках, близких к номинальной, то выгодно, чтобы значение kнг [смотрите формулу (10)] было близко к единице. Если машина работает в основном при малых нагрузках, то выгодно, чтобы значение kнг [смотрите формулу (10)] было соответственно меньше.
Источник: Вольдек А. И., «Электрические машины. Учебник для технических учебных заведений» – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.
Источник
Видео
Измерение КПД генератора.
Тест КПД между классическим Генератор и ДСГМ
Как определить мощность, частоту вращения, двигателя без бирки или шильдика самому и просто
Генераторы на постоянных магнитах и их КПД
Про КПД генераторов, зависимость кпд от просадки напряжения
УЛЬТРАКРУТОЙ ГЕНЕРАТОР С НАИВЫСШИМ КПД😁
КПД двигателя и как его увеличить?
Стенд для измерение КПД генератора
Потери и кпд машин постоянного тока
Как самостоятельно рассчитать мощность генератора?
Определение полезной мощности источника тока физической формулой
Содержание
- Двухполюсник и его эквивалентная схема
- ÐдиниÑÑ Ð¸Ð·Ð¼ÐµÑÐµÐ½Ð¸Ñ Ð¼Ð¾ÑноÑÑи
- Принцип действия
- 21.Принцип работы центробежного насоса.
- Что такое КПД ИТ
- Вопросы и задания для самоконтроля
- 1.
 11. Работа и мощность тока
11. Работа и мощность тока - ФоÑмÑÐ»Ñ Ð¼Ð¾ÑноÑÑи Ñока
- Виды электродвигателей
- Общие характеристики двигателей
- МОЩНОСТЬ, ВЫДЕЛЯЕМАЯ ВО ВНЕШНЕЙ ЦЕПИ
- Реактивный коэффициент
- Вращательный момент
- Как найти активную, реактивную и полную мощность
- От чего зависит мощность тока
- Виды мощности постоянного тока
- Мгновенная мощность
- Активная мощность
- Реактивная мощность
- Полная мощность
- Формула работы в физике
- Формула для общего случая
- Разрядная емкость источника
- Отношение – полезная мощность
Двухполюсник и его эквивалентная схема
Двухполюсник представляет собой электрическую цепь, содержащую две точки присоединения к другим цепям. Бывает два вида электрических цепей:
- цепи, содержащие источник тока или напряжения;
- двухполюсники, не являющиеся источниками.
Первые характеризуются электрическими параметрами: силой тока, напряжением и импедансом. Для расчёта параметров таких двухполюсников предварительно производят замену реальных элементов цепи на идеальные элементы. Комбинация, которая получается в результате подобной замены, называется эквивалентной схемой.
Для расчёта параметров таких двухполюсников предварительно производят замену реальных элементов цепи на идеальные элементы. Комбинация, которая получается в результате подобной замены, называется эквивалентной схемой.
Внимание! При работе со сложными электрическими схемами с учётом того, что устройство работает на одной частоте, допустимо преобразовывать последовательные и параллельные ветви до получения простой схемы, доступной для расчёта параметров. Второй вид двухполюсников можно охарактеризовать только величиной внутреннего сопротивления
Второй вид двухполюсников можно охарактеризовать только величиной внутреннего сопротивления.
ÐдиниÑÑ Ð¸Ð·Ð¼ÐµÑÐµÐ½Ð¸Ñ Ð¼Ð¾ÑноÑÑи
1 ÐÑ (ваÑÑ) – моÑноÑÑÑ Ñока в 1 Ð (ампеÑ) в пÑоводнике, Ð¼ÐµÐ¶Ð´Ñ ÐºÐ¾Ð½Ñами коÑоÑого поддеÑживаеÑÑÑ Ð½Ð°Ð¿ÑÑжение 1 Ð (волÑÑ).
ÐÑÐ¸Ð±Ð¾Ñ Ð´Ð»Ñ Ð¸Ð·Ð¼ÐµÑÐµÐ½Ð¸Ñ Ð¼Ð¾ÑноÑÑи ÑлекÑÑиÑеÑкого Ñока назÑваеÑÑÑ Ð²Ð°ÑÑмеÑÑ. Также ÑоÑмÑла моÑноÑÑи Ñока позволÑÐµÑ Ð¾Ð¿ÑеделÑÑÑ Ð¼Ð¾ÑноÑÑÑ Ñ Ð¿Ð¾Ð¼Ð¾ÑÑÑ Ð²Ð¾Ð»ÑÑмеÑÑа и ампеÑмеÑÑа.
Также ÑоÑмÑла моÑноÑÑи Ñока позволÑÐµÑ Ð¾Ð¿ÑеделÑÑÑ Ð¼Ð¾ÑноÑÑÑ Ñ Ð¿Ð¾Ð¼Ð¾ÑÑÑ Ð²Ð¾Ð»ÑÑмеÑÑа и ампеÑмеÑÑа.
ÐнеÑиÑÑÐµÐ¼Ð½Ð°Ñ ÐµÐ´Ð¸Ð½Ð¸Ñа моÑноÑÑи – кÐÑ (киловаÑÑ), ÐÐÑ (гигаваÑÑ), мÐÑ (милливаÑÑ) и дÑ. С ÑÑим ÑвÑÐ·Ð°Ð½Ñ Ð¸ некоÑоÑÑе внеÑиÑÑемнÑе единиÑÑ Ð¸Ð·Ð¼ÐµÑÐµÐ½Ð¸Ñ ÑабоÑÑ, коÑоÑÑе ÑаÑÑо иÑполÑзÑÑÑ Ð² бÑÑÑ, напÑÐ¸Ð¼ÐµÑ (киловаÑÑ·ÑаÑ). ÐоÑколÑÐºÑ 1кÐÑ = 103ÐÑ, а 1Ñ = 3600Ñ, Ñо
1кÐÑÂ·Ñ = 103ÐÑ·3600Ñ = 3,6·106ÐÑÂ·Ñ = 3,6·106Ðж.
Принцип действия
По закону Архимеда ток в проводнике создает магнитное поле, в котором действует сила F1. Если из этого проводника изготовить металлическую рамку и поместить ее в поле под углом 90°, то края будут испытывать силы, направленные в противоположную сторону относительно друг друга. Они создают крутящий момент относительно оси, который начинает ее вращать. Витки якоря обеспечивают постоянное кручение. Поле создается электрическими или постоянными магнитами. Первый вариант выполнен в виде обмотки катушки на стальном сердечнике. Таким образом, ток рамки генерирует индукционное поле в обмотке электромагнита, которое порождает электродвижущую силу.
Поле создается электрическими или постоянными магнитами. Первый вариант выполнен в виде обмотки катушки на стальном сердечнике. Таким образом, ток рамки генерирует индукционное поле в обмотке электромагнита, которое порождает электродвижущую силу.
Рассмотрим более подробно работу асинхронных двигателей на примере установок с фазным ротором. Такие машины работают от переменного тока с частотой вращения якоря, не равной пульсации магнитного поля. Поэтому их еще называют индукционными. Ротор приводится в движение за счет взаимодействия электрического тока в катушках с магнитным полем.
Когда во вспомогательной обмотке отсутствует напряжение, устройство находится в состоянии покоя. Как только на контактах статора появляется электрический ток, образуется постоянное в пространстве магнитное поле с пульсацией +Ф и -Ф. Его можно представить в виде следующей формулы:
nпр = nобр = f1 × 60 ÷ p = n1
где:
nпр – количество оборотов, которое совершает магнитное поле в прямом направлении, об/мин;
nобр – число оборотов поля в обратном направлении, об/мин;
f1 – частота пульсации электрического тока, Гц;
p – количество полюсов;
n1 – общее число оборотов в минуту.
Испытывая пульсации магнитного поля, ротор получает начальное движение. По причине неоднородности воздействия потока, он будет развиваться крутящий момент. По закону индукции, в короткозамкнутой обмотке образуется электродвижущая сила, которая генерирует ток. Его частота пропорциональна скольжению ротора. Благодаря взаимодействию электрического тока с магнитным полем создается крутящий момент вала.
Для расчетов производительности существуют три формулы мощности асинхронного электродвигателя. По сдвигу фаз используют
S = P ÷ cos (alpha), где:
S – полная мощность, измеряемая в Вольт-Амперах.
P – активная мощность, указываемая в Ваттах.
alpha – сдвиг фаз.
Под полной мощностью понимаются реальный показатель, а под активной – расчетный.
21.Принцип работы центробежного насоса.
Устройство:
Основной
рабочий орган ц-б насоса – свободно
вращающееся внутри спиралевидного
корпуса колесо, насаженное на вал. Между
дисками колеса – лопасти, плавно
изогнутые в сторону, противоположную
направлению вращения колеса. Внутренние
Внутренние
поверхности дисков и поверхности лопаток
образуют т.н. межлопастные каналы колеса,
при работе заполненные перекачиваемой
жидкостью. Всасывание и нагнетание
жидкости происходит равномерно и
непрерывно под действием центробежной
силы, возникающей при вращении колеса.
Принцип
работы:
При
переходе жидкости из канала рабочего
колеса в корпус происходит резкое
снижение скорости, в результате чего
кинетическая энергия жидкости превращается
в потенциальную энергию давления,
которое необходимо для подачи жидкости
на заданную высоту. При этом в центре
колеса создается разрежение, и вследствие
этого жидкость непрерывно поступает
по всасывающему трубопроводу в корпус
насоса, а затем в межлопастные каналы
рабочего колеса. Если перед пуском ц-б
насоса всасывающий трубопровод и корпус
не залиты жидкостью, то возникающего
разрежения будет недостаточно для
подъема жидкости в насос (из-за зазоров
между колесом и корпусом). Чтобы жидкость
Чтобы жидкость
не выливалась из насоса, на всасывающем
трубопроводе устанавливают обратный
клапан. Для отвода жидкости в корпусе
насоса есть расширяющаяся спиралевидная
камера: жидкость сначала поступает в
эту камеру, а затем в нагнетательный
трубопровод.
Что такое КПД ИТ
Когда речь идёт о кпд источника тока, также рассматривают полезную и полную работу, совершаемую двухполюсником. Перемещая электроны во внешней цепи, он выполняет полезную работу, двигая их по всей цепи, включая и свою внутреннюю, он производит полную работу.
В виде формул это выглядит так:
- А полезн. = q*U = I*U*t = I2*R*t;
- А полн. = q*ε = I* ε*t = I2*(R+r)*t.
где:
- q – количество энергии, Дж;
- U – напряжение, В;
- ε – ЭДС, В;
- I – ток, А;
- R – сопротивление нагрузки, Ом;
- r – импеданс источника, Ом;
- t – время, за которое совершается работа, с.
С учётом этого можно выразить мощности двухполюсника:
- Р полезн.
 = А полезн./t = I*U = I2*R;
= А полезн./t = I*U = I2*R; - P полн. = А полн./t = I*ε = I2*(R+r).
Формула кпд источников тока имеет вид:
η = Р полезн./P полн.= U/ε = R/ R+r.
Вопросы и задания для самоконтроля
- Запишите закон Джоуля-Ленца в интегральной и дифференциальной формах.
- Что такое ток короткого замыкания?
- Что такое полная мощность?
- Как вычисляется к.п.д. источника тока?
- Докажите, что наибольшая полезная мощность выделяется при равенстве внешнего и внутреннего сопротивлений цепи.
- Верно ли утверждение, что мощность, выделяемая во внутренней части цепи, постоянна для данного источника?
- К зажимам батарейки карманного фонаря присоединили вольтметр, который показал 3,5 В.
- Затем вольтметр отсоединили и на его место подключили лампу, на цоколе которой было написано: Р=30 Вт, U=3,5 В. Лампа не горела.
- Объясните явление.
- При поочерёдном замыкании аккумулятора на сопротивления R1 и R2 в них за одно и то же время выделилось равное количество тепла.
 Определите внутреннее сопротивление аккумулятора.
Определите внутреннее сопротивление аккумулятора.
1.11. Работа и мощность тока
При протекании тока по однородному участку цепи электрическое поле совершает работу. За время Δt по цепи протекает заряд Δq = I Δt. Электрическое поле на выделенном учестке совершает работу
U12работой электрического тока
Если обе части формулы
RIt
Это соотношение выражает закон сохранения энергии для однородного участка цепи.
Работа ΔA электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в тепло ΔQ, выделяющееся на проводнике.
Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж. Джоулем и Э. Ленцем и носит название закона Джоуля–Ленца.
Мощность электрического тока равна отношению работы тока ΔA к интервалу времени Δt, за которое эта работа была совершена:
Работа электрического тока в СИ выражается в джоулях (Дж), мощность – в ваттах (Вт).
Рассмотрим теперь полную цепь постоянного тока, состоящую из источника с электродвижущей силой и внутренним сопротивлением r и внешнего однородного участка с сопротивлением R. записывается в виде
Умножив обе части этой формулы на Δq = IΔt, мы получим соотношение, выражающее закон сохранения энергии для полной цепи постоянного тока:
Первый член в левой части ΔQ = R I2Δt – тепло, выделяющееся на внешнем участке цепи за время Δt, второй член ΔQист = r I2Δt – тепло, выделяющееся внутри источника за то же время.
Выражение IΔt равно работе сторонних сил ΔAст, действующих внутри источника.
При протекании электрического тока по замкнутой цепи работа сторонних сил ΔAст преобразуется в тепло, выделяющееся во внешней цепи (ΔQ) и внутри источника (ΔQист).
Следует обратить внимание, что в это соотношение не входит работа электрического поля. При протекании тока по замкнутой цепи электрическое поле работы не совершает; поэтому тепло производится одними только сторонними силами, действующими внутри источника
Роль электрического поля сводится к перераспределению тепла между различными участками цепи.
Внешняя цепь может представлять собой не только проводник с сопротивлением R, но и какое-либо устройство, потребляющее мощность, например, электродвигатель постоянного тока. В этом случае под R нужно понимать эквивалентное сопротивление нагрузки. Энергия, выделяемая во внешней цепи, может частично или полностью преобразовываться не только в тепло, но и в другие виды энергии, например, в механическую работу, совершаемую электродвигателем. Поэтому вопрос об использовании энергии источника тока имеет большое практическое значение.
Полная мощность источника, то есть работа, совершаемая сторонними силами за единицу времени, равна
коэффициентом полезного действия источника
На рис. 1.11.1 графически представлены зависимости мощности источника Pист, полезной мощности P, выделяемой во внешней цепи, и коэффициента полезного действия η от тока в цепи I для источника с ЭДС, равной , и внутренним сопротивлением r. Ток в цепи может изменяться в пределах от I = 0 (при ) до (при R = 0).
| Рисунок 1.11.1.Зависимость мощности источника Pист, мощности во внешней цепи P и КПД источника η от силы тока |
Из приведенных графиков видно, что максимальная мощность во внешней цепи Pmax, равная
Rr
I → 0R → ∞P
ФоÑмÑÐ»Ñ Ð¼Ð¾ÑноÑÑи Ñока
Ðод моÑноÑÑÑÑ Ñока Ñак же, как и в меÑанике, понимаÑÑ ÑабоÑÑ, коÑоÑÐ°Ñ Ð²ÑполнÑеÑÑÑ Ð·Ð° единиÑÑ Ð²Ñемени. РаÑÑÑиÑаÑÑ Ð¼Ð¾ÑноÑÑÑ, Ð·Ð½Ð°Ñ ÑабоÑÑ, коÑоÑÑÑ Ð²ÑполнÑÐµÑ ÑлекÑÑиÑеÑкий Ñок за некоÑоÑÑй пÑомежÑÑок вÑемени, Ð¿Ð¾Ð¼Ð¾Ð¶ÐµÑ ÑизиÑеÑÐºÐ°Ñ ÑоÑмÑла.
Ток, напÑÑжение, моÑноÑÑÑ Ð² ÑлекÑÑоÑÑаÑике ÑвÑÐ·Ð°Ð½Ñ ÑавенÑÑвом, коÑоÑое можно вÑвеÑÑи из ÑоÑмÑÐ»Ñ A = UIt. Ðо ней опÑеделÑÑÑ ÑабоÑÑ, коÑоÑÑÑ Ð²ÑполнÑÐµÑ ÑлекÑÑиÑеÑкий Ñок:
P = A/t = UIt/t = UI Таким обÑазом, ÑоÑмÑла моÑноÑÑи поÑÑоÑнного Ñока на лÑбом ÑÑаÑÑке Ñепи вÑÑажаеÑÑÑ ÐºÐ°Ðº пÑоизведение ÑÐ¸Ð»Ñ Ñока на напÑÑжение Ð¼ÐµÐ¶Ð´Ñ ÐºÐ¾Ð½Ñами ÑÑаÑÑка.
Виды электродвигателей
По источнику питания приводы разделяют на работающие от:
- Постоянного тока.
- Переменного тока.
По принципу работы их, в свою очередь, делят на:
- Коллекторные.
- Вентильные.
- Асинхронные.
- Синхронные.
Вентильные двигатели не относят к отдельному классу, так как их устройство является вариацией коллекторного привода. В их конструкцию входит электронный преобразователь и датчик положения ротора. Обычно их интегрируют вместе с платой управления. За их счет происходит согласованная коммутация якоря.
Синхронные и асинхронные двигатели работают исключительно от переменного тока. Управление оборотами происходит с помощью сложной электроники. Асинхронные делятся на:
- Трехфазные.
- Двухфазные.
- Однофазные.
Теоретическая формула мощности трехфазного электродвигателя при соединении в звезду или треугольником
P = 3 * Uф * Iф * cos(alpha).
Однако для линейных значений напряжения и тока она выглядит как
P = 1,73 × Uф × Iф × cos(alpha).
Это будет реальный показатель, сколько мощности двигатель забирает из сети.
Синхронные подразделяются на:
- Шаговые.
- Гибридные.
- Индукторные.
- Гистерезисные.
- Реактивные.
В своей конструкции шаговые двигатели имеют постоянные магниты, поэтому их не относят к отдельной категории. Управление работой механизмов производится с помощью частотных преобразователей. Существуют также универсальные двигатели, которые функционируют от постоянного и переменного тока.
Общие характеристики двигателей
Все моторы имеют общие параметры, которые используются в формуле определения мощности электродвигателя. На их основе можно рассчитать свойства машины. В разной литературе они могут называться по-разному, но означают они одно и то же. В список таких параметров входит:
- Крутящий момент.
- Мощность двигателя.

- Коэффициент полезного действия.
- Номинальное количество оборотов.
- Момент инерции ротора.
- Расчетное напряжение.
- Электрическая константа времени.
Вышеуказанные параметры необходимы, прежде всего, для определения эффективности электрических установок, работающих за счет механической силы двигателей. Расчетные величины дают лишь приблизительное представление о реальных характеристиках изделия. Однако эти показатели часто используют в формуле мощность электродвигателя. Именно она определяет результативность машин.
МОЩНОСТЬ, ВЫДЕЛЯЕМАЯ ВО ВНЕШНЕЙ ЦЕПИ
. (2)
Из формулы (2) видно, что при коротком замыкании цепи (R0) и при Rэта мощность равна нулю. При всех других конечных значениях R мощность Р1> 0. Следовательно, функция Р1 имеет максимум. Значение R, соответствующее максимальной мощности, можно получить, дифференцируя Р1 по R и приравнивая первую производную к нулю:
. (3)
Из формулы (3), с учётом того, что R и r всегда положительны, а Е ? 0, после несложных алгебраических преобразований получим:
R= r. (4)
(4)
Следовательно, мощность, выделяемая во внешней цепи, достигает наибольшего значения при сопротивлении внешней цепи равном внутреннему сопротивлению источника тока.
При этом сила тока в цепи (5)
равна половине тока короткого замыкания. При этом мощность, выделяемая во внешней цепи, достигает своего максимального значения, равного
. (6)
Когда источник замкнут на внешнее сопротивление, то ток протекает и внутри источника и при этом на внутреннем сопротивлении источника выделяется некоторое количество тепла. Мощность, затрачиваемая на выделение этого тепла равна
. (7)
Следовательно, полная мощность, выделяемая во всей цепи , определится формулой
= I2(R+r) = IE (8)
Реактивный коэффициент
По-другому он называется коэффициентом мощности и является безразмерной величиной, вводимой для вычисления реактивной составляющей. Говоря научным языком, он показывает, насколько сдвигается фаза переменного тока, протекающего через нагрузку, от возникшего на ней напряжения. Численно он принимается равным косинусу сдвига. Математически это сдвиг интерпретируется как косинус угла между векторными значениями тока и напряжения.
Численно он принимается равным косинусу сдвига. Математически это сдвиг интерпретируется как косинус угла между векторными значениями тока и напряжения.
Простыми же словами, коэффициент мощности, обозначаемый φ, указывает на ту часть расходуемой электроэнергии, которая преобразуется в полезную работу. Например, при cos φ = 0,9 девяносто процентов от полной энергии уйдёт на совершение полезного действия, а остальные десять будут считаться потерями. Поэтому если в паспорте на какой-либо прибор указано, что мощность изделия составляет 500 Вт, а cos φ = 0,5, то полный расход его энергии будет составлять 500/0,5 = 250 ВА.
То есть коэффициент φ находится из отношения потребляемой устройством энергии к значению полной мощности. Нередко в паспорте оборудования указывается и составляющая φ (характер нагрузки). Она может быть резистивно-ёмкостной или резистивно-индуктивной. При этом сам коэффициент соответственно является опережающим или отстающим.
Если же напряжение в цепи изменяется по синусоидальному закону, а ток по несинусоидальному, то нагрузка никакой реактивной составляющей иметь не будет, а коэффициент принимается равным главной волне (первой гармонике).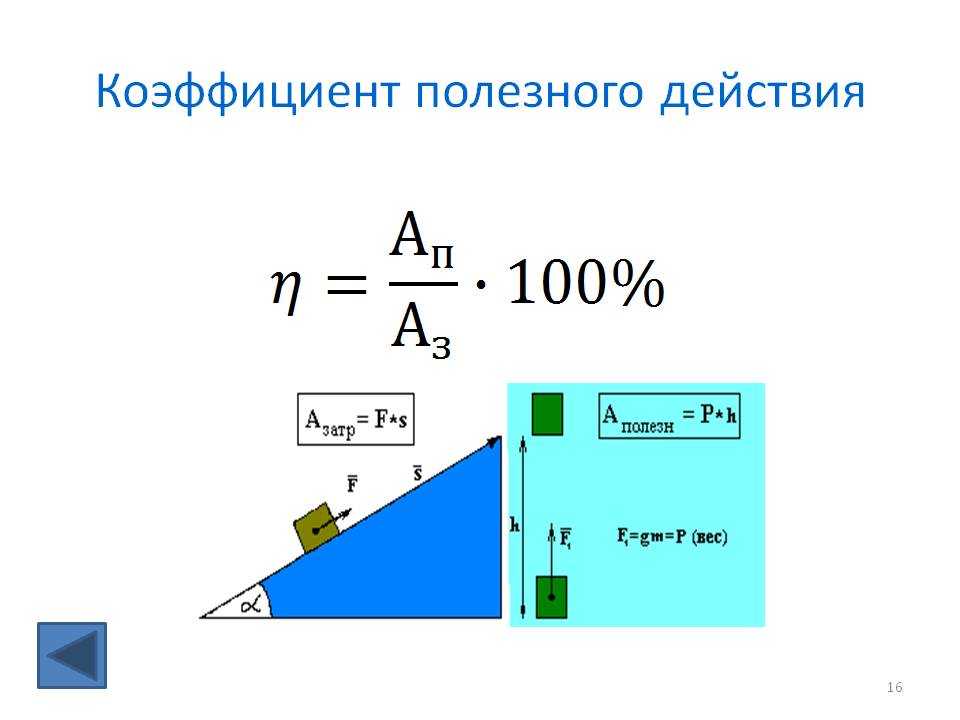 Под несинусоидальными понимаются искажения электрического сигнала, связанные с гармониками, преобладающими над основной частотой.
Под несинусоидальными понимаются искажения электрического сигнала, связанные с гармониками, преобладающими над основной частотой.
В математике формулой для нахождения коэффициента мощности является выражение: cos φ= P/S. Поэтому чем больше его значение, тем меньше потребляет устройство энергию из сети. Существуют различные способы поднятия значения cos φ, даже до максимального значения, равного единице, называемые коррекцией. Наиболее эффективным является добавление в схему сложного электронного узла, размещаемого на входе устройства.
Вращательный момент
Этот термин имеет несколько синонимов: момент силы, момент двигателя, Вращательный момент, вертящий момент. Все они используются для обозначения одного показателя, хотя с точки зрения физики эти понятия не всегда тождественны.
В целях унификации терминологии были разработаны стандарты, которые приводят все к единой системе. Поэтому в технической документации всегда используются словосочетание “крутящий момент”. Он представляет собой векторную физическую величину, которая равна произведению векторных значений силы и радиуса. Вектор радиуса проводится от оси вращения к точке приложенной силы. С точки зрения физики разница между крутящим и вращательным моментом заключается в точке прикладывания силы. В первом случае это внутреннее усилие, во втором – внешнее. Измеряется величина в ньютон-метрах. Однако в формуле мощности электродвигателя крутящий момент используется как основное значение.
Он представляет собой векторную физическую величину, которая равна произведению векторных значений силы и радиуса. Вектор радиуса проводится от оси вращения к точке приложенной силы. С точки зрения физики разница между крутящим и вращательным моментом заключается в точке прикладывания силы. В первом случае это внутреннее усилие, во втором – внешнее. Измеряется величина в ньютон-метрах. Однако в формуле мощности электродвигателя крутящий момент используется как основное значение.
Рассчитывается он как
M = F × r, где:
M – крутящий момент, Нм;
F – прикладываемая сила, H;
r – радиус, м.
Для расчета номинального вращающего момента привода используют формулу
Мном = 30Рном ÷ pi × нном, где:
Рном – номинальная мощность электрического двигателя, Вт;
нном – номинальное число оборотов, мин-1.
Соответственно, формула номинальной мощности электродвигателя бедует выглядеть следующим образом:
Рном = Мном * pi*нном / 30.
Обычно все характеристики указаны в спецификации. Но бывает, что приходится работать с совершенно новыми установками, информацию о которых найти очень сложно. Для расчета технических параметров таких устройств берут данные их аналогов. Также всегда известны только номинальные характеристики, которые даются в спецификации. Реальные данные необходимо рассчитывать самостоятельно.
Как найти активную, реактивную и полную мощность
Активная мощность относится к энергии, которая необратимо расходуется источником за единицу времени для выполнения потребителем какой-либо полезной работы. В процессе потребления, как уже было отмечено, она преобразуется в другие виды энергии.
В цепи переменного тока значение активной мощности определяется, как средний показатель мгновенной мощности за установленный период времени. Следовательно, среднее значение за этот период будет зависеть от угла сдвига фаз между током и напряжением и не будет равной нулю, при условии присутствия на данном участке цепи активного сопротивления. Последний фактор и определяет название активной мощности. Именно через активное сопротивление электроэнергия необратимо преобразуется в другие виды энергии.
Последний фактор и определяет название активной мощности. Именно через активное сопротивление электроэнергия необратимо преобразуется в другие виды энергии.
При выполнении расчетов электрических цепей широко используется понятие реактивной мощности. С ее участием происходят такие процессы, как обмен энергией между источниками и реактивными элементами цепи. Данный параметр численно будет равен амплитуде, которой обладает переменная составляющая мгновенной мощности цепи.
Существует определенная зависимость реактивной мощности от знака угла ф, отображенного на рисунке. В связи с этим, она будет иметь положительное или отрицательное значение. В отличие от активной мощности, измеряемой в ваттах, реактивная мощность измеряется в вар – вольт-амперах реактивных. Итоговое значение реактивной мощности в разветвленных электрических цепях представляет собой алгебраическую сумму таких же мощностей у каждого элемента цепи с учетом их индивидуальных характеристик.
Основной составляющей полной мощности является максимально возможная активная мощность при заранее известных токе и напряжении. При этом, cosф равен 1, когда отсутствует сдвиг фаз между током и напряжением. В состав полной мощности входит и реактивная составляющая, что хорошо видно из формулы, представленной выше. Единицей измерения данного параметра служит вольт-ампер (ВА).
При этом, cosф равен 1, когда отсутствует сдвиг фаз между током и напряжением. В состав полной мощности входит и реактивная составляющая, что хорошо видно из формулы, представленной выше. Единицей измерения данного параметра служит вольт-ампер (ВА).
Что такое активная и реактивная электроэнергия, мощность
Как найти реактивную мощность
Активное и реактивное сопротивление
Компенсация реактивной мощности в электрических сетях
Активное и индуктивное сопротивление кабелей – таблица
Онлайн калькулятор расчета тока по мощности
От чего зависит мощность тока
Мощность тока, различных приборов и оборудования зависит сразу от двух основных величин – силы тока и напряжения. Чем выше ток, тем больше значение мощности, соответственно, при повышении напряжения, мощность также возрастает. Если напряжение и сила тока увеличиваются одновременно, то мощность электрического тока будет возрастать как произведение той и другой величины: N = I x U.
Очень часто возникает вопрос, в чем измеряется мощность тока? Основной единицей измерения этой величины является 1 ватт (Вт). Таким образом, 1 ватт является мощностью устройства, потребляющего ток силой в 1 ампер, при напряжении 1 вольт. Подобной мощностью обладает, например, лампочка от обычного карманного фонарика.
Таким образом, 1 ватт является мощностью устройства, потребляющего ток силой в 1 ампер, при напряжении 1 вольт. Подобной мощностью обладает, например, лампочка от обычного карманного фонарика.
Расчетное значение мощности позволяет точно определить расход электрической энергии. Для этого необходимо взять произведение мощности и времени. Сама формула выглядит так: W = IUt где W является расходом электроэнергии, произведение IU – мощностью, а t – количеством отработанного времени. Например, чем больше продолжается работа электрического двигателя, тем большая работа им совершается. Соответственно возрастает и потребление электроэнергии.
Формула электрической мощности
В чем измеряется мощность электрического тока
Как найти мощность
Активная реактивная и полная мощность
Расчет тока по мощности и напряжению
Мощность (P) Время (T) Энергия (W)
Виды мощности постоянного тока
Любая мощностная величина определяется работой, которая совершается за определенную единицу времени. Чаще всего ею становится секунда. Она означает величину, характеризующую, насколько быстро совершается работа. Касаемо электрической мощности это расход электроэнергии за одну секунду.
Чаще всего ею становится секунда. Она означает величину, характеризующую, насколько быстро совершается работа. Касаемо электрической мощности это расход электроэнергии за одну секунду.
Мощностная характеристика тока соответствует отношению его работы ко времени
Работой тока называется процесс превращения электроэнергии в какую-либо другую энергию (механическую, тепловую или световую). Именно по мощности, которая обозначается буквой «P» или «W», и оценивается работоспособность электротока.
К сведению! Вообще у тока постоянного значения нет активной и реактивной P. Для этого вида сети характерна только мгновенная характеристика.
Мгновенная мощность
Если говорить о сетях переменного электротока, то рассматриваемая величина в них, как и электроток или напряжение, регулярно меняет свои значения. Это напрямую влияет на другие параметры. При константном течении зарядов все остается неизменным. Именно поэтому и возникает термин «мгновенная мощность».
Силы в сети регулярного тока остаются неизменными и равняются мгновенным их значениям, взятым в произвольный момент времени. Такую характеристику можно высчитать по мгновенным значениям. Для этого подходит формула мощности постоянного тока в цепи: P = I * U.
Такую характеристику можно высчитать по мгновенным значениям. Для этого подходит формула мощности постоянного тока в цепи: P = I * U.
Рассматриваемая величина может быть найдена из произведения силы электротока и напряжения
Если сеть пассивна и в ней соблюдается закон Ома, то справедливо равенство. В случае подключения источника ЭДС нужна другая формула: P = I * E, где E — это электродвижущая сила.
Активная мощность
Активная мощность — это среднее за период значение мгновенной P. При активной P происходит конвертация мощности тока в энергию любого вида (механическую, световую или тепловую). Подобный перевод электротока нельзя выполнить в обратном направлении. Активный тип также измеряется в ваттах. 1 Ватт равен 1 вольту умноженному на 1 ампер.
Работа неразрывно связана с определением мощностных характеристик
К сведению! В бытовых и уж тем более промышленных масштабах единицу измерения ватт никогда не используют. Для этих целей задействуют показатели на порядок выше: мегаватты в киловатты.
Реактивная мощность
Реактивная мощностная характеристика определяет нагрузку, которая создается электрическими устройствами определенными колебаниями энергии электромагнитного поля в сетях синусоидального тока переменной частоты. Она равна произведению среднеквадратичных значений напряжения и силы тока, умноженных на синус угла, на который сдвигается фаза между ними. Реактивный параметр неразрывно связан с полной P и активным параметром.
Все основные величины могут быть найдены с использованием закона Ома
Если говорить про физический смыл реактивности, то он представляет собой некую энергию, которая перекачивается из источника к реактивным элементам приемника (конденсатор, обмотка генератора, катушка индуктивности и т. д.), а потом возвращается обратно в источник за время одного периода колебаний.
Полная мощность
Полная P электротока представляет собой значение, соответствующее произведению силы электротока и напряжения в цепи. Она неразрывно связана с активной и реактивной величинами и определяется следующим уравнением: , где Sos = полная мощность, а P и Q — ее активная и реактивная характеристики соответственно.
Общая мощность, которую можно представить в виде кружки пива
Если говорить проще, то активная P есть везде, где присутствует нагрузка активного плана. Например, в спиральных нагревателях, сопротивлении проводов и т. д. Реактивный параметр характерен для реактивной нагрузки, которая имеется в элементах индуктивности или емкости.
Формула работы в физике
Для механической работы формула несложна: A = F x S. Если расшифровать, она равна приложенной силе на путь, на протяжении которого эта сила действовала. Например, мы поднимаем груз массой 15 кг на высоту 2 метра. Механическая работа по преодолению силы тяжести будет равна F x S = m x g x S. То есть, 15 x 9,8 x 2 = 294 Дж. Если речь идет о количестве теплоты, то A в этом случае равняется изменению количества теплоты. Например, на плите нагрели воду. Ее внутренняя энергия изменилась, она увеличилась на величину, равную произведению массы воды на удельную теплоемкость на количество градусов, на которое она нагрелась.
Формула для общего случая
Так как напряжение — это работа, то, умножив её на количество перенесённых зарядов, получится энергия, затраченная для перемещения частиц от одного края проводника к другому. Энергия, в общем понимании, это работа за единицу времени. Поэтому можно записать следующее выражение Pab = A/dt, где:
- dt — интервал времени, за который все свободные заряды были перенесены;
- A — непосредственно сама работа.
Исходя из определения, данного силе тока, она практически является зарядом. В случае изменения во времени ток можно описать выражением I = q/dt. Тогда, исходя из этой формулы, верным будет утверждение, что q = I*dt. Если подставить полученную формулу вместо q в выражение, описывающее мощность, получится Pab = U* (I*dt/dt) = U*I.
Если время изменения бесконечно мало, то можно принять, что напряжение и ток практически не изменяются. В результате мгновенная электрическая мощность будет равна P (t) = u (t)*i (t). Как видно из формулы, значение мощности для любой точки времени будет прямо пропорционально мгновенным значениям тока и разности потенциалов. При этом если цепь неидеальная, то она содержит определённое сопротивление. Используя закон Ома для участка цепи, формулу для нахождения мгновенной мощности можно переписать в виде P (t) = i (t)2*R = u (t)2/R.
При этом если цепь неидеальная, то она содержит определённое сопротивление. Используя закон Ома для участка цепи, формулу для нахождения мгновенной мощности можно переписать в виде P (t) = i (t)2*R = u (t)2/R.
Мощность одновременно связана сразу с несколькими величинами и соответствует полной работе, затрачиваемой на перемещение некоторого количества кулонов за единицу времени (одну секунду). Из определения следует, что одно и то же значение мощности можно получить разными способами, например, уменьшая силу тока, но увеличивая напряжение. Такой подход и используется при передаче энергии на большие расстояния. Для этого применяются трансформаторы, понижающие и повышающие ток.
Разрядная емкость источника
Величина, зависящая от силы тока разряда, называется разрядной ёмкостью источника. Это электрический заряд, который отдаёт источник в процессе эксплуатации в зависимости от тока нагрузки. Эту величину можно считать постоянной условно. Так, стартерный аккумулятор, имеющий разрядную ёмкость С = 55 А*ч, при токе разряда 5,5 А проработает 10 часов. При запусках холодного или имеющего неисправность автомобиля аккумулятор можно разрядить за несколько минут.
При запусках холодного или имеющего неисправность автомобиля аккумулятор можно разрядить за несколько минут.
Для того чтобы найти остаточную разрядную ёмкость, производят циклы «заряд – разряд». Они выполняются при помощи нагрузочных сопротивлений. Разряд на нагрузочное сопротивление производят до минимально допустимых значений плотности электролита. При этом замеряется время работы под нагрузкой. Это актуально при сезонном обслуживании аккумуляторов для выявления процессов саморазряда.
Разрядная ёмкость автомобильного аккумулятора
Внутреннее сопротивление источников тока – важная величина. Методы, применяемые для её снижения, являются прямыми путями увеличения отдаваемой мощности источника, значит, повышения производительности двухполюсников. Правильное измерение и вычисление импеданса эквивалентных схем позволяют приблизить двухполюсник к идеальному источнику.
Отношение – полезная мощность
Мощность, потребляемая двигателем из сети, всегда больше полезной мощности двигателя и зависит от типа двигателя. Отношение полезной мощности двигателя к мощности, потребляемой из сети, называется коэффициентом полезного действия двигателя. Мощность, получаемая в результате вычитания полезной мощности двигателя от мощности, потребляемой из сети, превращается в тепло и приводит к нагреванию двигателя.
Отношение полезной мощности двигателя к мощности, потребляемой из сети, называется коэффициентом полезного действия двигателя. Мощность, получаемая в результате вычитания полезной мощности двигателя от мощности, потребляемой из сети, превращается в тепло и приводит к нагреванию двигателя.
Основной характеристикой, определяющей достоинства двигателя, является его коэффициент полезного действия. Он равен отношению полезной мощности, развиваемой двигателем к полным энергетическим затратам. Если реактивный двигатель развивает силу тяги F и летит со скоростью и, то, очевидно, полезная мощность, развиваемая им, равна Fv. С другой стороны, полная затраченная энергия равна q GH, где G – расход горючего в единицу времени, а Н – теплотворная способность горючего.
Источник тока ( генератор) всегда должен создавать полную мощность, но только некоторая ее часть является полезной, а другая часть неизбежно теряется на внутреннем сопротивлении генератора.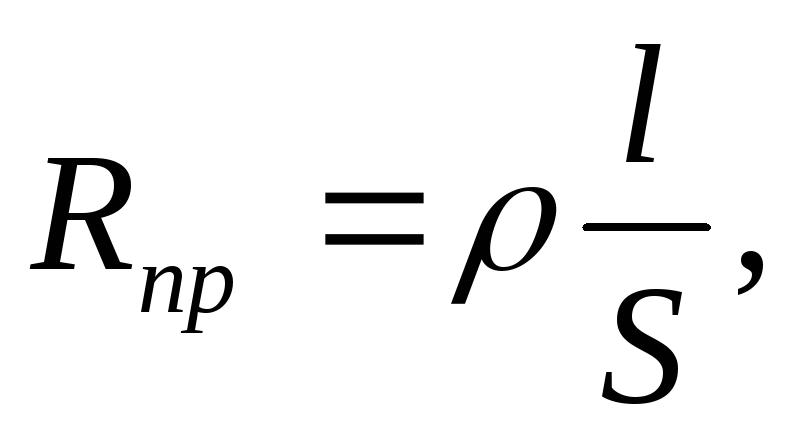 Он равен отношению полезной мощности к полной. Иначе говоря, кпд показывает, какую долю полной мощности составляет полезная мощность.
Он равен отношению полезной мощности к полной. Иначе говоря, кпд показывает, какую долю полной мощности составляет полезная мощность.
Коэффициент полезного действия ( КПД) учитывает все виды потерь, связанных с преобразованием механической энергии двигателя в энергию движущей жидкости. Определяется КПД отношением полезной мощности к мощности, потребляемой насосом.
Естественным способом улучшения cos cp является полная загрузка асинхронных двигателей. КПД определяется отношением полезной мощности ЛГ2 к подводимой NI. У большинства двигателей КПД достигает максимума ( 65 – 95 %) при нагрузке, равной 75 % номинальной. Благодаря этому обеспечивается экономичность двигателей при преобладающих на практике режимах нагружения.
Гидравлический КПД представляет собой отношение полезной мощности насоса к сумме полезной мощности и мощности, затраченной на преодоление гидравлических сопротивлений в насосе. Объемным КПД называют отношение полезной мощности насоса к сумме полезной мощности и мощности, потерянной с утечками. Механический КПД насоса есть величина, выражающая относительную долю механических потерь в насосе.
Механический КПД насоса есть величина, выражающая относительную долю механических потерь в насосе.
Под коэффициентом полезного действия приемной антенны понимается обычно отношение полезной мощности, выделенной на нагрузке ( на сопротивлении приемника), к полной мощности, принятой антенной из поля.
Такой подход к разделению потерь не изменяет общей картины процессов, происходящих в герметической машине, так как полный коэффициент полезного действия равен отношению полезной мощности, затрачиваемой на выполнение транспортировки жидкости или газа, к мощности, потребляемой электродвигателем из сети. Однако следует помнить, что потери на трение выделяются в виде тепла в небольшом пространстве между статором и ротором, и если не будет обеспечена надлежащая циркуляция жидкости, то очень скоро наступит сильный нагрев ее и, следовательно электродвигателя.
Различают мощность, потребляемую насосом, и полезную мощность насоса. Полезной называют мощность, сообщаемую насосом подаваемой жидкой среде. Отношение полезной мощности к потребляемой мощности насоса является КПД насоса.
Полезной называют мощность, сообщаемую насосом подаваемой жидкой среде. Отношение полезной мощности к потребляемой мощности насоса является КПД насоса.
| Режим усиления класса В в двухтактной ступени. |
А когда на сетке нет переменного напряжения, то нет полезной мощности, и вся подводимая мощность расходуется на нагрев анода. Теоретически кпд ступени в режиме класса А не выше 40 – 45 %, а практически он ниже. Таким образом, режим класса А невыгоден в отношении полезной мощности и характеризуется низким кпд. Второй режим, называемый усилением класса В, состоит в том, что рабочая точка устанавливается в начале нижнего изгиба характеристики. Импульсы анодного тока получаются только от положительных полуволн переменного напряжения сетки. График усиления в режиме класса В для одной лампы показан на рис. 9.35 а. Колебания анодного тока сильно искажены по сравнению с колебаниями на сетке.
Энергетические соотношения | Электротехника
Активная мощность и потери. Напомним, что потребляемая двигателем электрическая мощность преобразуется в механическую. Эта мощность представляет собой активную мощность. Как и в любой другой машине, мощность, потребляемая двигателем из сети Р1, отличается от мощности на валу двигателя Р2 на значение мощности потерь в самом двигателе ∆ Р, т. е. P1 = P2 + ∆P.
Естественно, что чем меньше потери ∆ Р , тем больше КПД двигателя. Мощность потерь, нагревающих машину, складывается из мощности электрических, магнитных и механических потерь. Электрические потери ∆ РЭ возникают в обмотках статора и ротора, т. е. ∆ РЭ = ∆ РЭ1 + ∆ РЭ2 (здесь ∆ РЭ1 — потери в обмотке статора и ∆ РЭ2 — потери в обмотке ротора). Магнитные потери в магнитопроводе ∆ РМ1 возникают за счет явлений гистерезиса и вихревых токов в статоре ∆ РМ1 и в роторе ∆ РМ2 , т. е. ∆РМ = ∆РМ1 + ∆РМ2.
е. ∆РМ = ∆РМ1 + ∆РМ2.
Потери механические вызваны силами трения в подшипниках, в скользящем контакте (щетка – кольцо), и ротора о воздушную среду ∆РМЕХ . На основе изложенного
Р1 = Р2 + ∆ РЭ1 +∆РЭ2 + ∆РМ1 + ∆РМ2 + ∆РМЕХ. (3.29)
Выражение (3.29) можно упростить, если пренебречь магнитными потерями в пакете ротора из-за их малости в сравнении с другими слагаемыми. Действительно, частота тока ротора в пределах до номинальной нагрузки составляет 1—4 Гц. При такой частоте тока, а значит, и поля потери из-за гистерезиса и вихревых токов в роторе весьма малы. Поэтому практически можно считать, что
Р1 = Р2 + ∆ РЭ1 +∆РЭ2 + ∆РМ1 + ∆РМ2 + ∆РМЕХ (3.30)
Электромагнитная мощность и мощность на валу. Мощность, передаваемая магнитным полем от статора к ротору РЭМ, есть мощность, потребляемая из сети за вычетом потерь в статоре, т. е.
Мощность, передаваемая магнитным полем от статора к ротору РЭМ, есть мощность, потребляемая из сети за вычетом потерь в статоре, т. е.
РЭМ = Р1 — ∆РЭ1 — ∆РМ1 (3.31)
Мощность может быть представлена как произведение момента на угловую скорость Ω1 , т. е.
РЭМ = Ω1М (3.32)
Механическая мощность ротора РМЕХ , вращающегося с угловой скоростью Ω, может быть представлена как
РМЕХ=ΩМ (3.33)
Потери в роторе составляют ∆РЭ2, поэтому
РЭМ = РМЕХ + ∆РЭ2(3.34)
Мощность на валу двигателя Р2отличается от механической на значение механических потерь ∆РМЕХ , т.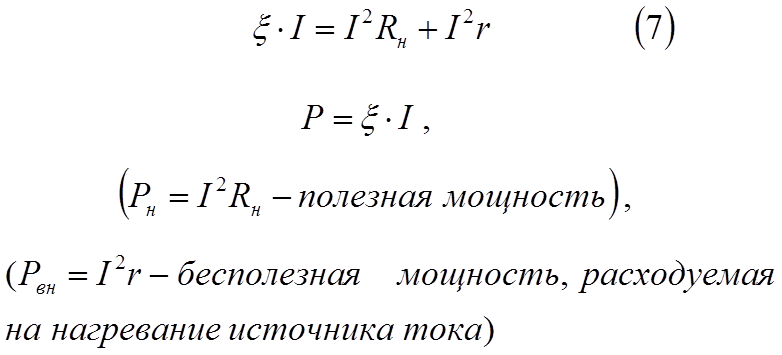 е.
е.
Р2 = РМЕХ – ∆РМЕХ (3.35)
Исходя из введенных понятий и формул (3.30)-(3.35), можно для лучшей наглядности показать при помощи энергетической диаграммы, представленной на рис. 3.20, распределение мощностей и потерь в асинхронном двигателе. Если подставить в формулу (3.34) значения мощностей через моменты (3.32) и (3.33), то можно показать, что электрические потери ротора пропорциональны скольжению.
Чем ближе частота вращения ротора к частоте вращения поля, тем электрические потери меньше. Следует отметить, что магнитные потери ∆РМ при изменении нагрузки двигателя от холостого хода до номинальной, так же как и в трансформаторе, являются постоянной величиной, т. е. не зависят от нагрузки.
Механические потери ∆РМЕХ также практически не зависят от нагрузки.
КПД двигателя. КПД двигателя есть отношение полезной мощности, т. е. мощности на валу двигателя (паспортной_мощности) Р2 , к потребляемой мощности из сети , т. е. .
КПД двигателя есть отношение полезной мощности, т. е. мощности на валу двигателя (паспортной_мощности) Р2 , к потребляемой мощности из сети , т. е. .
Если постоянные потери обозначать через ∆Рс(∆Рс=∆Рм+∆Рмех), а переменные потери ∆Рэ, то
КПД двигателя изменяется в зависимости от нагрузки двигателя, поэтому в формуле КПД следует учесть коэффициент загрузки . Так как переменные электрические потери ∆Рэпропорциональны квадрату тока, формула КПД аналогична формуле КПД для трансформатора, т. е.
. (3.36)
Обычно КПД асинхронного двигателя составляет 0,75 — 0,95.
Большее значение КПД имеет двигатель большей мощности. График ,построенный согласно (3.36) изображен на рис. 3.21.
График ,построенный согласно (3.36) изображен на рис. 3.21.
Коэффициент мощности. Кроме активной мощности P1, двигатель потребляет реактивную мощность Q1, в основном необходимую для образования вращающегося магнитного поля. Коэффициент мощности при синусоидальном токе
При холостом ходе cosφ1 имеет малое значение (примерно 0,1), так как активная мощность расходуется только на относительно небольшие потери в статоре и небольшие механические потери, а реактивная мощность имеет постоянное значение, так как магнитный поток постоянен.
С увеличением нагрузки активная мощность увеличивается, а реактивная мощность в пределах до номинальной нагрузки имеет неизменное значение. В результате cosφ1 увеличивается, однако при дальнейшем увеличении нагрузки сказывается увеличение потока рассеяния, т. е. реактивная мощность увеличивается и cosφ1 начинает уменьшаться. Кривая зависимости коэффициента мощности от загрузки двигателя показана на рис. 3.21.
е. реактивная мощность увеличивается и cosφ1 начинает уменьшаться. Кривая зависимости коэффициента мощности от загрузки двигателя показана на рис. 3.21.
Учитывая изложенное, следует сделать вывод, что необходимо стремиться к тому, чтобы двигатель работал при нагрузке, близкой к номинальной (β = 1).
Коэффициент полезного действия (КПД). Что такое коэффициент полезного действия (КПД) и как рассчитать его по формуле
Содержание
- 1 Что такое КПД
- 1.1 Примеры расчета КПД
- 1.2 Единицы измерения
- 2 От чего зависит величина КПД
- 2.1 Как обозначается
- 2.2 Символ, обозначающий КПД
- 3 Мощность и КПД
- 3.1 Формула работы в физике
- 4 Мощность и коэффициент полезного действия электродвигателей
- 4.1 Магнитные потери мощности
- 4.2 Механические и электрические потери
- 4.3 Добавочные потери
- 4.
 4 КПД и его зависимость от нагрузки
4 КПД и его зависимость от нагрузки
- 5 В чем измеряется КПД
- 5.1 Для чего нужен расчет КПД
- 5.2 Примеры расчета КПД
- 6 КПД в механике
- 6.1 Ради чего все это затеяли?
- 6.2 За счет чего процесс происходит?
- 7 КПД в термодинамике
- 7.1 Идеальная тепловая машина: цикл Карно
- 7.2 КПД в электродинамике
- 8 Физическая формула КПД
- 8.1 Применение в разных сферах физики
- 8.2 Видео
- 9 Как устроен тепловой двигатель
- 9.1 Идеальный тепловой двигатель Карно
- 10 Трактовка понятия
Что такое КПД
Коэффициент полезного действия машины или механизма – это важная величина, характеризующая энергоэффективность данного устройства. Понятие используется и в повседневной жизни. Например, когда человек говорит, что КПД его усилий низкий, это значит, что сил затрачено много, а результата почти нет. Величина измеряет отношение полезной работы ко всей совершенной работе.
Согласно формуле, чтобы найти величину, нужно полезную работу разделить на всю совершенную работу. Или полезную энергию разделить на всю израсходованную энергию. Этот коэффициент всегда меньше единицы. Работа и энергия измеряется в Джоулях. Поделив Джоули на Джоули, получаем безразмерную величину. КПД иногда называют энергоэффективностью устройства.
Если попытаться объяснить простым языком, то представим, что мы кипятим чайник на плите. При сгорании газа образуется определенное количество теплоты. Часть этой теплоты нагревает саму горелку, плиту и окружающее пространство. Остальная часть идет на нагревание чайника и воды в нем. Чтобы рассчитать энергоэффективность данной плитки, нужно будет разделить количество тепла, требуемое для нагрева воды до температуры кипения на количество тепла, выделившееся при горении газа.
Данная величина всегда ниже единицы. Например, для любой атомной электростанции она не превышает 35%. Причиной является то, что электростанция представляет собой паровую машину, где нагретый за счет ядерной реакции пар вращает турбину. Большая часть энергии идет на нагрев окружающего пространства. Тот факт, что η не может быть равен 100%, следует из второго начала термодинамики.
Большая часть энергии идет на нагрев окружающего пространства. Тот факт, что η не может быть равен 100%, следует из второго начала термодинамики.
Примеры расчета КПД
Пример 1. Нужно рассчитать коэффициент для классического камина. Дано: удельная теплота сгорания березовых дров – 107Дж/кг, количество дров – 8 кг. После сгорания дров температура в комнате повысилась на 20 градусов. Удельная теплоемкость кубометра воздуха – 1,3 кДж/ кг*град. Общая кубатура комнаты – 75 кубометров.
Чтобы решить задачу, нужно найти частное или отношение двух величин. В числителе будет количество теплоты, которое получил воздух в комнате (1300Дж*75*20=1950 кДж ). В знаменателе – количество теплоты, выделенное дровами при горении (10000000Дж*8 =8*107 кДж). После подсчетов получаем, что энергоэффективность дровяного камина – около 2,5%. Действительно, современная теория об устройстве печей и каминов говорит, что классическая конструкция не является энергоэффективной. Это связано с тем, что труба напрямую выводит горячий воздух в атмосферу. Для повышения эффективности устраивают дымоход с каналами, где воздух сначала отдает тепло кладке каналов, и лишь потом выходит наружу. Но справедливости ради, нужно отметить, что в процессе горения камина нагревается не только воздух, но и предметы в комнате, а часть тепла выходит наружу через элементы, плохо теплоизолированные – окна, двери и т.д.
После подсчетов получаем, что энергоэффективность дровяного камина – около 2,5%. Действительно, современная теория об устройстве печей и каминов говорит, что классическая конструкция не является энергоэффективной. Это связано с тем, что труба напрямую выводит горячий воздух в атмосферу. Для повышения эффективности устраивают дымоход с каналами, где воздух сначала отдает тепло кладке каналов, и лишь потом выходит наружу. Но справедливости ради, нужно отметить, что в процессе горения камина нагревается не только воздух, но и предметы в комнате, а часть тепла выходит наружу через элементы, плохо теплоизолированные – окна, двери и т.д.
Пример 2. Автомобиль проделал путь 100 км. Вес машины с пассажирами и багажом – 1400 кг. При этом было затрачено14 литров бензина. Найти: КПД двигателя.
Для решения задачи необходимо отношение работы по перемещению груза к количеству тепла, выделившемуся при сгорании топлива. Количество тепла также измеряется в Джоулях, поэтому не придется приводить к другим единицам.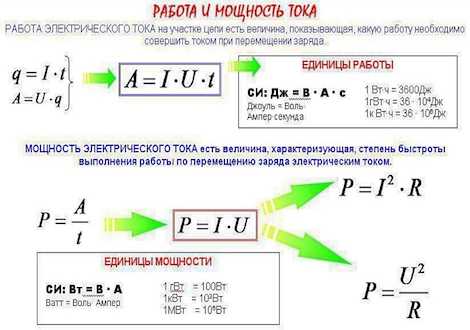 A будет равна произведению силы на путь( A=F*S=m*g*S). Сила равна произведению массы на ускорение свободного падения. Полезная работа = 1400 кг x 9,8м/с2 x 100000м=1,37*108 Дж
A будет равна произведению силы на путь( A=F*S=m*g*S). Сила равна произведению массы на ускорение свободного падения. Полезная работа = 1400 кг x 9,8м/с2 x 100000м=1,37*108 Дж
Удельная теплота сгорания бензина – 46 МДж/кг=46000 кДж/кг. Восемь литров бензина будем считать примерно равными 8 кг. Тепла выделилось 46*106*14=6.44*108 Дж. В результате получаем η ≈21%.
Единицы измерения
Коэффициент полезного действия – величина безразмерная, то есть не нужно ставить какую-либо единицу измерения. Но эту величину можно выразить и в процентах. Для этого полученное в результате деления по формуле число необходимо умножить на 100%. В школьном курсе математики рассказывали, что процент – этот одна сотая чего-либо. Умножая на 100 процентов, мы показываем, сколько в числе сотых.
От чего зависит величина КПД
Эта величина зависит от того, насколько общая совершенная работа может переходить в полезную. Прежде всего, это зависит от самого устройства механизма или машины. Инженеры всего мира бьются над тем, чтобы повышать КПД машин. Например, для электромобилей коэффициент очень высок – больше 90%.
Инженеры всего мира бьются над тем, чтобы повышать КПД машин. Например, для электромобилей коэффициент очень высок – больше 90%.
А вот двигатель внутреннего сгорания, в силу своего устройства, не может иметь η, близкий к 100 процентам. Ведь энергия топлива не действует непосредственно на вращающиеся колеса. Энергия рассеивается на каждом передаточном звене. Слишком много передаточных звеньев, и часть выхлопных газов все равно выходит в выхлопную трубу.
Как обозначается
В русских учебниках обозначается двояко. Либо так и пишется – КПД, либо обозначается греческой буквой η. Эти обозначения равнозначны.
Символ, обозначающий КПД
Символом является греческая буква эта η. Но чаще все же используют выражение КПД.
Мощность и КПД
Мощность механизма или устройства равна работе, совершаемой в единицу времени. Работа(A) измеряется в Джоулях, а время в системе Си – в секундах. Но не стоит путать понятие мощности и номинальной мощности. Если на чайнике написана мощность 1 700 Ватт, это не значит, что он передаст 1 700 Джоулей за одну секунду воде, налитой в него. Это мощность номинальная. Чтобы узнать η электрочайника, нужно узнать количество теплоты(Q), которое должно получить определенное количество воды при нагреве на энное количество градусов. Эту цифру делят на работу электрического тока, выполненную за время нагревания воды.
Это мощность номинальная. Чтобы узнать η электрочайника, нужно узнать количество теплоты(Q), которое должно получить определенное количество воды при нагреве на энное количество градусов. Эту цифру делят на работу электрического тока, выполненную за время нагревания воды.
Величина A будет равна номинальной мощности, умноженной на время в секундах. Q будет равно объему воды, умноженному на разницу температур на удельную теплоемкость. Потом делим Q на A тока и получаем КПД электрочайника, примерно равное 80 процентам. Прогресс не стоит на месте, и КПД различных устройств повышается, в том числе бытовой техники.
Напрашивается вопрос, почему через мощность нельзя узнать КПД устройства. На упаковке с оборудованием всегда указана номинальная мощность. Она показывает, сколько энергии потребляет устройство из сети. Но в каждом конкретном случае невозможно будет предсказать, сколько конкретно потребуется энергии для нагрева даже одного литра воды.
Например, в холодной комнате часть энергии потратится на обогрев пространства. Это связано с тем, что в результате теплообмена чайник будет охлаждаться. Если, наоборот, в комнате будет жарко, чайник закипит быстрее. То есть КПД в каждом из этих случаев будет разным.
Это связано с тем, что в результате теплообмена чайник будет охлаждаться. Если, наоборот, в комнате будет жарко, чайник закипит быстрее. То есть КПД в каждом из этих случаев будет разным.
Формула работы в физике
Для механической работы формула несложна: A = F x S. Если расшифровать, она равна приложенной силе на путь, на протяжении которого эта сила действовала. Например, мы поднимаем груз массой 15 кг на высоту 2 метра. Механическая работа по преодолению силы тяжести будет равна F x S = m x g x S. То есть, 15 x 9,8 x 2 = 294 Дж. Если речь идет о количестве теплоты, то A в этом случае равняется изменению количества теплоты. Например, на плите нагрели воду. Ее внутренняя энергия изменилась, она увеличилась на величину, равную произведению массы воды на удельную теплоемкость на количество градусов, на которое она нагрелась.
Мощность и коэффициент полезного действия электродвигателей
Электрические двигатели имеют высокий коэффициент полезного действия (КПД), но все же он далек от идеальных показателей, к которым продолжают стремиться конструкторы. Все дело в том, что при работе силового агрегата преобразование одного вида энергии в другой проходит с выделение теплоты и неминуемыми потерями. Рассеивание тепловой энергии можно зафиксировать в разных узлах двигателя любого типа. Потери мощности в электродвигателях являются следствием локальных потерь в обмотке, в стальных деталях и при механической работе. Вносят свой вклад, пусть и незначительный, дополнительные потери.
Все дело в том, что при работе силового агрегата преобразование одного вида энергии в другой проходит с выделение теплоты и неминуемыми потерями. Рассеивание тепловой энергии можно зафиксировать в разных узлах двигателя любого типа. Потери мощности в электродвигателях являются следствием локальных потерь в обмотке, в стальных деталях и при механической работе. Вносят свой вклад, пусть и незначительный, дополнительные потери.
Расчет КПД.
Магнитные потери мощности
При перемагничивании в магнитном поле сердечника якоря электродвигателя происходят магнитные потери. Их величина, состоящая из суммарных потерь вихревых токов и тех, что возникают при перемагничивании, зависят от частоты перемагничивания, значений магнитной индукции спинки и зубцов якоря. Немалую роль играет толщина листов используемой электротехнической стали, качество ее изоляции.
Механические и электрические потери
Механические потери при работе электродвигателя, как и магнитные, относятся к числу постоянных.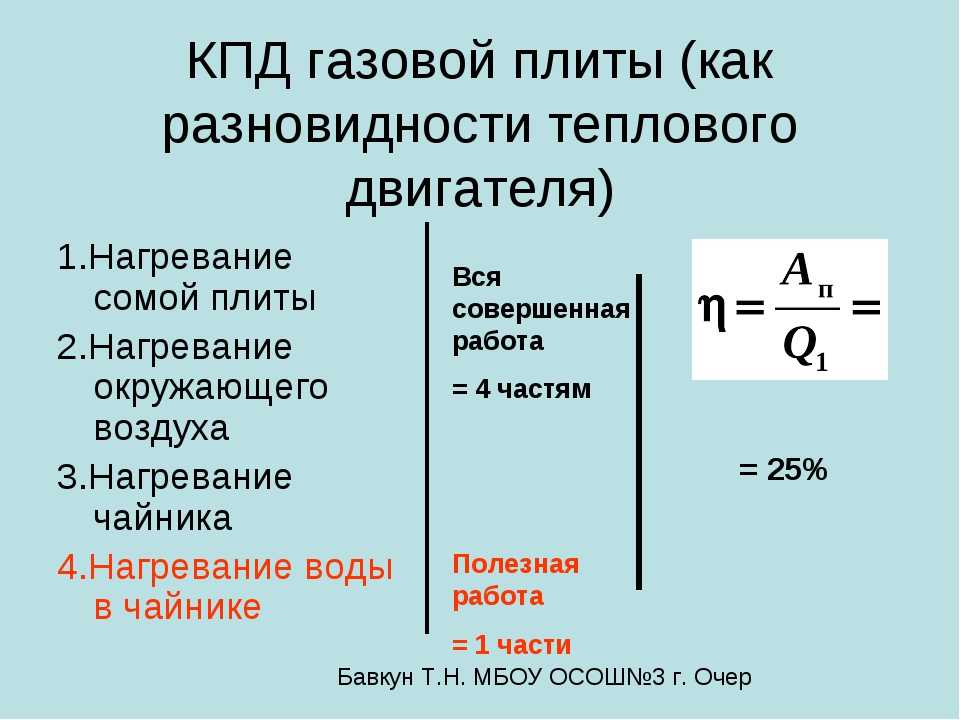 Они складываются из потерь на трение подшипников, на трение щеток, на вентиляцию двигателя. Минимизировать механические потери позволяет использование современных материалов, эксплуатационные характеристики которых совершенствуются из года в год. В отличие от них электрические потери не являются постоянными и зависят от уровня нагрузки электродвигателя. Чаще всего они возникают вследствие нагрева щеток, щеточного контакта.
Они складываются из потерь на трение подшипников, на трение щеток, на вентиляцию двигателя. Минимизировать механические потери позволяет использование современных материалов, эксплуатационные характеристики которых совершенствуются из года в год. В отличие от них электрические потери не являются постоянными и зависят от уровня нагрузки электродвигателя. Чаще всего они возникают вследствие нагрева щеток, щеточного контакта.
Падает коэффициент полезного действия (КПД) от потерь в обмотке якоря и цепи возбуждения. Механические и электрические потери вносят основной вклад в изменение эффективности работы двигателя.
Добавочные потери
Добавочные потери мощности в электродвигателях складываются из потерь, возникающих в уравнительных соединениях, из потерь из-за неравномерной индукции в стали якоря при высокой нагрузке. Вносят свой вклад в общую сумму добавочных потерь вихревые токи, а также потери в полюсных наконечниках. Точно определить все эти значения довольно сложно, поэтому их сумму принимают обычно равной в пределах 0,5-1%. Эти цифры используют при расчете общих потерь для определения КПД электродвигателя.
Эти цифры используют при расчете общих потерь для определения КПД электродвигателя.
КПД и его зависимость от нагрузки
Коэффициент полезного действия (КПД) электрического двигателя это отношение полезной мощности силового агрегата к мощности потребляемой. Этот показатель у двигателей, мощностью до 100 кВт находится в пределах от 0,75 до 0,9. для более мощных силовых агрегатов КПД существенно выше: 0,9-0,97. Определив суммарные потери мощности в электродвигателях можно достаточно точно вычислить коэффициент полезного действия любого силового агрегата. Этот метод определения КПД называется косвенным и он может применяться для машин различной мощности.
Для маломощных силовых агрегатов часто используют метод непосредственной нагрузки, заключающийся в измерениях потребляемой двигателем мощности. КПД электрического двигателя не является величиной постоянной, своего максимума он достигает при нагрузках около 80% мощности.
Достигает он пикового значения быстро и уверенно, но после своего максимума начинает медленно уменьшаться. Это связывают с возрастанием электрических потерь при нагрузках, более 80% от номинальной мощности. Падение коэффициента полезного действия не велико, что позволяет говорить о высоких показателях эффективности электродвигателей в широком диапазоне мощностей.
Это связывают с возрастанием электрических потерь при нагрузках, более 80% от номинальной мощности. Падение коэффициента полезного действия не велико, что позволяет говорить о высоких показателях эффективности электродвигателей в широком диапазоне мощностей.
В чем измеряется КПД
Коэффициент полезного действия (кпд), характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии; определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой; обозначается обычно h = Wпол/Wcyм.
В электрических двигателях кпд — отношение совершаемой (полезной) механической работы к электрической энергии, получаемой от источника; в тепловых двигателях — отношение полезной механической работы к затрачиваемому количеству теплоты; в электрических трансформаторах — отношение электромагнитной энергии, получаемой во вторичной обмотке, к энергии, потребляемой первичной обмоткой.
Для вычисления кпд разные виды энергии и механическая работа выражаются в одинаковых единицах на основе механического эквивалента теплоты, и др. аналогичных соотношений. В силу своей общности понятие кпд позволяет сравнивать и оценивать с единой точки зрения такие различные системы, как атомные реакторы, электрические генераторы и двигатели, теплоэнергетические установки, полупроводниковые приборы, биологические объекты и т. д.
аналогичных соотношений. В силу своей общности понятие кпд позволяет сравнивать и оценивать с единой точки зрения такие различные системы, как атомные реакторы, электрические генераторы и двигатели, теплоэнергетические установки, полупроводниковые приборы, биологические объекты и т. д.
Из-за неизбежных потерь энергии на трение, на нагревание окружающих тел и т. п. кпд всегда меньше единицы. Соответственно этому кпд выражается в долях затрачиваемой энергии, т. е. в виде правильной дроби или в процентах, и является безразмерной величиной. Кпд тепловых электростанций достигает 35—40%, двигателей внутреннего сгорания — 40—50%, динамомашин и генераторов большой мощности—95%, трансформаторов—98%.
В чем измеряется КПД.
Кпд процесса фотосинтеза составляет обычно 6—8%, у хлореллы он достигает 20—25%. У тепловых двигателей в силу второго начала термодинамики кпд имеет верхний предел, определяемый особенностями термодинамического цикла (кругового процесса), который совершает рабочее вещество. Наибольшим кпд обладает Карно цикл. Различают кпд отдельного элемента (ступени) машины или устройства и кпд, характеризующий всю цепь преобразований энергии в системе. Кпд первого типа в соответствии с характером преобразования энергии может быть механическим, термическим и т. д. Ко второму типу относятся общий, экономический, технический и др. виды кпд. Общий кпд системы равен произведению частных кпд, или кпд ступеней.
Наибольшим кпд обладает Карно цикл. Различают кпд отдельного элемента (ступени) машины или устройства и кпд, характеризующий всю цепь преобразований энергии в системе. Кпд первого типа в соответствии с характером преобразования энергии может быть механическим, термическим и т. д. Ко второму типу относятся общий, экономический, технический и др. виды кпд. Общий кпд системы равен произведению частных кпд, или кпд ступеней.
В технической литературе кпд иногда определяют т. о., что он может оказаться больше единицы. Подобная ситуация возникает, если определять кпд отношением Wпол/Wзатр, где Wпол — используемая энергия, получаемая на «выходе» системы, Wзатр — не вся энергия, поступающая в систему, а лишь та её часть, для получения которой производятся реальные затраты.
Например, при работе полупроводниковых термоэлектрических обогревателей (тепловых насосов) затрата электроэнергии меньше количества теплоты, выделяемой термоэлементом. Избыток энергии черпается из окружающей среды. При этом, хотя истинный кпд установки меньше единицы, рассмотренный кпд h = Wпол/Wзатр может оказаться больше единицы.
Примеры расчета КПД.
Для чего нужен расчет КПД
Коэффициент полезного действия электрической цепи – это отношение полезного тепла к полному. Для ясности приведем пример. При нахождении КПД двигателя можно определить, оправдывает ли его основная функция работы затраты потребляемого электричества. То есть его расчет даст ясную картину, насколько хорошо устройство преобразовывает получаемую энергию. Обратите внимание! Как правило, коэффициент полезного действия не имеет величины, а представляет собой процентное соотношение либо числовой эквивалент от 0 до 1. КПД находят по общей формуле вычисления, для всех устройств в целом. Но чтобы получить его результат в электрической цепи, вначале потребуется найти силу электричества.
По физике известно, что любой генератор тока имеет свое сопротивление, которое еще принято называть внутренняя мощность. Помимо этого значения, источник электричества также имеет свою силу. Дадим значения каждому элементу цепи: сопротивление – r; сила тока – Е; резистор (внешняя нагрузка) – R. Полная цепь Итак, чтобы найти силу тока, обозначение которого будет – I, и напряжение на резисторе – U, потребуется время – t, с прохождением заряда q = lt. Рассчитать работу источника тока можно по следующей формуле: A = Eq = EIt. В связи с тем, что сила электричества постоянна, работа генератора целиком преобразуется в тепло, выделяемое на R и r. Такое количество можно рассчитать по закону Джоуля-Ленца: Q = I2 + I2 rt = I2 (R + r) t.
Формулы расчета КПД.
Затем приравниваются правые части формулы: EIt = I2 (R + r) t. Осуществив сокращение, получается расчет: E = I(R + r). Произведя у формулы перестановку, в итоге получается: I = E R + r. Данное итоговое значение будет являться электрической силой в данном устройстве. Произведя таким образом предварительный расчет, теперь можно определить КПД.
Произведя таким образом предварительный расчет, теперь можно определить КПД.
Расчет КПД электрической цепи Мощность, получаемая от источника тока, называется потребляемой, определение ее записывается – P1. Если эта физическая величина переходит от генератора в полную цепь, она считается полезной и записывается – Р2. Чтобы определить КПД цепи, необходимо вспомнить закон сохранения энергии.
В соответствии с ним, мощность приемника Р2 будет всегда меньше потребляемой мощности Р1. Это объясняется тем, что в процессе работы в приемнике всегда происходит неизбежная пустая трата преобразуемой энергии, которая расходуется на нагревание проводов, их оболочки, вихревых токов и т.д. Чтобы найти оценку свойств превращения энергии, необходим КПД, который будет равен отношению мощностей Р2 и Р1.
Итак, зная все значения показателей, составляющих электроцепи, находим ее полезную и полную работу: А полезная. = qU = IUt =I2Rt; А полная = qE = IEt = I2(R+r)t. В соответствии этих значений, найдем мощности источника тока: Р2 = А полезная /t = IU = I2 R; P1 = А полная /t = IE = I2 (R + r). Произведя все действия, получаем формулу КПД: n = А полезная / А полная = Р2 / P1 =U / E = R / (R +r). У этой формулы получается, что R выше бесконечности, а n выше 1, но при всем этом ток в цепи остается в низком положении, и его полезная мощность мала.
Произведя все действия, получаем формулу КПД: n = А полезная / А полная = Р2 / P1 =U / E = R / (R +r). У этой формулы получается, что R выше бесконечности, а n выше 1, но при всем этом ток в цепи остается в низком положении, и его полезная мощность мала.
Каждый желает найти КПД повышенного значения. Для этого необходимо найти условия, при которых P2 будет максимален. Оптимальные значения будут: dP2 / dR = 0. Далее определить КПД можно формулами: P2 = I2 R = (E / R + r)2 R; dP2 / dR = (E2 (R + r)2 — 2 (r + R) E2 R) / (R + r)4 = 0; E2 ((R + r) -2R) = 0. В данном выражении Е и (R + r) не равны 0, следовательно, ему равно выражение в скобках, то есть (r = R). Тогда получается, что мощность имеет максимальное значение, а коэффициент полезного действия = 50 %. Как видно, найти коэффициент полезного действия электрической цепи можно самостоятельно, не прибегая к услугам специалиста. Главное –соблюдать последовательность в расчетах и не выходить за рамки приведенных формул.
youtube.com/embed/B0rBgKtPEZg?feature=oembed» frameborder=»0″ allowfullscreen=»» allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture»>
Примеры расчета КПД
Пример 1. Нужно рассчитать коэффициент для классического камина. Дано: удельная теплота сгорания березовых дров – 107Дж/кг, количество дров – 8 кг. После сгорания дров температура в комнате повысилась на 20 градусов. Удельная теплоемкость кубометра воздуха – 1,3 кДж/ кг*град. Общая кубатура комнаты – 75 кубометров.
Чтобы решить задачу, нужно найти частное или отношение двух величин. В числителе будет количество теплоты, которое получил воздух в комнате (1300Дж*75*20=1950 кДж ). В знаменателе – количество теплоты, выделенное дровами при горении (10000000Дж*8 =8*107 кДж). После подсчетов получаем, что энергоэффективность дровяного камина – около 2,5%. Действительно, современная теория об устройстве печей и каминов говорит, что классическая конструкция не является энергоэффективной. Это связано с тем, что труба напрямую выводит горячий воздух в атмосферу.
Это связано с тем, что труба напрямую выводит горячий воздух в атмосферу.
Для повышения эффективности устраивают дымоход с каналами, где воздух сначала отдает тепло кладке каналов, и лишь потом выходит наружу. Но справедливости ради, нужно отметить, что в процессе горения камина нагревается не только воздух, но и предметы в комнате, а часть тепла выходит наружу через элементы, плохо теплоизолированные – окна, двери и т.д.
Расчет коэффициента полезного действия.
Пример 2. Автомобиль проделал путь 100 км. Вес машины с пассажирами и багажом – 1400 кг. При этом было затрачено14 литров бензина. Найти: КПД двигателя.
Для решения задачи необходимо отношение работы по перемещению груза к количеству тепла, выделившемуся при сгорании топлива. Количество тепла также измеряется в Джоулях, поэтому не придется приводить к другим единицам. A будет равна произведению силы на путь( A=F*S=m*g*S). Сила равна произведению массы на ускорение свободного падения. Полезная работа = 1400 кг x 9,8м/с2 x 100000м=1,37*108 Дж
Удельная теплота сгорания бензина – 46 МДж/кг=46000 кДж/кг. Восемь литров бензина будем считать примерно равными 8 кг. Тепла выделилось 46*106*14=6.44*108 Дж. В результате получаем η ≈21%.
Восемь литров бензина будем считать примерно равными 8 кг. Тепла выделилось 46*106*14=6.44*108 Дж. В результате получаем η ≈21%.
КПД в механике
Главный секрет заключается в том, что эта формула подойдет для всех видов КПД.
Запоминаем!КПД не может быть больше 100%. В реальной жизни и 100 не встречается, но больше сотни даже в задачах нет. Это значит, что если в задаче получается значение больше 100%, то мы в ответ пишем 100. И никак иначе.
КПД η = (Aполезная/Aзатраченная) * 100% η — коэффициент полезного действия [%] Aполезная — полезная работа [Дж] Aзатраченная — затраченная работа [Дж] |
Дальше мы просто заменяем полезную и затраченную работы на те величины, которые ими являются.
Давайте разберемся на примере задачи.
Задача
Чтобы вкатить санки массой 4 кг в горку длиной 12 метров, мальчик приложил силу в 15 Н. 2
2
За счет чего процесс происходит?
За счет мальчика, он же тянет санки. Значит затраченная работа равна механической работе
Механическая работа А = FS A — механическая работа [Дж] F — приложенная сила [Н] S — путь [м] |
Заменим формуле КПД полезную работу на потенциальную энергию, а затраченную — на механическую работу:
η = Eп/A * 100% = mgh/FS * 100%
Подставим значения:
η = 4*9,8*2/15*12 * 100% = 78,4/180 * 100% ≃ 43,6 %
Ответ: КПД процесса приблизительно равен 43,6 %
КПД в термодинамике
В термодинамике КПД — очень важная величина. Она полностью определяет эффективность такой штуки, как тепловая машина.
- Тепловой двигатель (машина) – это устройство, которое совершает механическую работу циклически за счет энергии, поступающей к нему в ходе теплопередачи.

Схема теплового двигателя выглядит так:
У теплового двигателя обязательно есть нагреватель, который (не может быть!) нагревает рабочее тело, передавая ему количество теплоты Q1 или Qнагревателя (оба варианта верны, это зависит лишь от учебника, в котором вы нашли формулу).
- Рабочее тело — это тело, на котором завязан процесс (чаще всего это газ). Оно расширяется при подводе к нему теплоты и сжимается при охлаждении. Часть переданного Q1 уходит на механическую работу A. Из-за этого производится движение.
Оставшееся количество теплоты Q2 или Qхолодильника отводится к холодильнику, после чего возвращается к нагревателю и процесс повторяется.
КПД такой тепловой машины будет равен:
КПД тепловой машины η = (Aполезная/Qнагревателя) * 100% η — коэффициент полезного действия [%] Aполезная — полезная работа (механическая) [Дж] Qнагревателя — количество теплоты, полученное от нагревателя[Дж] |
Если мы выразим полезную (механическую) работу через Qнагревателя и Qхолодильника, мы получим:
A = Qнагревателя — Qхолодильника.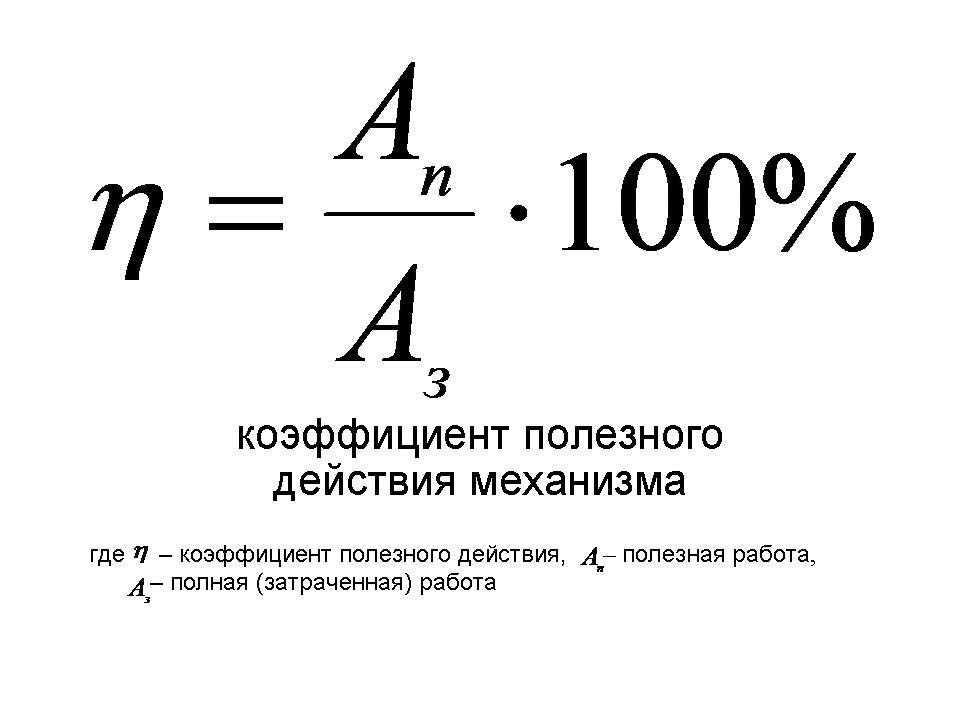
Подставим в числитель и получим такой вариант формулы.
КПД тепловой машины η = Qнагревателя — Qхолодильника/Qнагревателя * 100% η — коэффициент полезного действия [%] Qнагревателя — количество теплоты, полученное от нагревателя[Дж] Qхолодильника — количество теплоты, отданное холодильнику [Дж] |
А возможно ли создать тепловую машину, которая будет работать только за счет охлаждения одного тела? Точно нет! Если у нас не будет нагревателя, то просто нечего будет передавать на механическую работу. Любой такой процесс — когда энергия не приходит из ниоткуда — означал бы возможность существования вечного двигателя. Поскольку свидетельств такого процесса в мире не существует, то мы можем сделать вывод: вечный двигатель невозможен. Это второе начало термодинамики. |
Запишем его, чтобы не забыть:
Невозможно создать периодическую тепловую машину за счет охлаждения одного тела без изменений в других телах.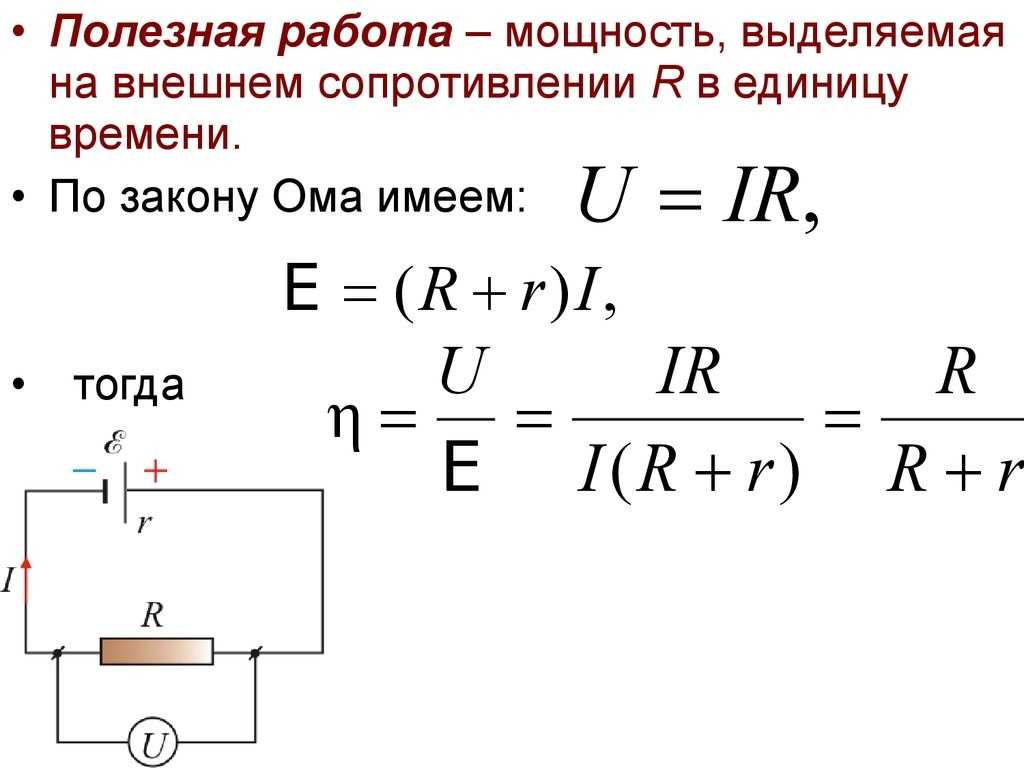
Задача
Найти КПД тепловой машины, если рабочее тело получило от нагревателя 20кДж, а отдало холодильнику 10 кДж.
Решение:
Возьмем формулу для расчета КПД:
η = Qнагревателя — Qхолодильника/Qнагревателя * 100%
Подставим значения:
η = 20 — 10/20 *100% = 50%
Ответ: КПД тепловой машины равен 50%
Идеальная тепловая машина: цикл Карно
Давайте еще чуть-чуть пофантазируем: какая она — идеальная тепловая машина. Кажется, что это та, у которой КПД равен 100%.
На самом деле понятие «идеальная тепловая машина» уже существует. Это тепловая машина, у которой в качестве рабочего тела взят идеальный газ. Такая тепловая машина работает по циклу Карно. Зависимость давления от объема в этом цикле выглядит следующим образом
А КПД для цикла Карно можно найти через температуры нагревателя и холодильника.
КПД цикла Карно η = Tнагревателя — Tхолодильника /Tнагревателя *100% η — коэффициент полезного действия [%] Tнагревателя — температура нагревателя[Дж] Tхолодильника — температура холодильника [Дж] |
КПД в электродинамике
Мы каждый день пользуемся различными электронными устройствами: от чайника до смартфона, от компьютера до робота-пылесоса — и у каждого устройства можно определить, насколько оно эффективно выполняет задачу, для которой оно предназначено, просто посчитав КПД.
Вспомним формулу:
КПД η = Aполезная/Aзатраченная *100% η — коэффициент полезного действия [%] Aполезная — полезная работа [Дж] Aзатраченная — затраченная работа [Дж] |
Для электрических цепей тоже есть нюансы. Давайте разбираться на примере задачи.
Задачка, чтобы разобраться
Найти КПД электрического чайника, если вода в нем приобрела 22176 Дж тепла за 2 минуты, напряжение в сети — 220 В, а сила тока в чайнике 1,4 А.
Решение:
Цель электрического чайника — вскипятить воду. То есть его полезная работа — это количество теплоты, которое пошло на нагревание воды. Оно нам известно, но формулу вспомнить все равно полезно
Количество теплоты, затраченное на нагревание Q = cm(tконечная-tначальная) Q — количество теплоты [Дж] c — удельная теплоемкость вещества [Дж/кг*˚C] m — масса [кг] tконечная — конечная температура [˚C] tначальная — начальная температура [˚C] |
Работает чайник, потому что в розетку подключен. 2)/R *t = UIt
2)/R *t = UIt
A — работа электрического тока [Дж]
I — сила тока [А]
U — напряжение [В]
R — сопротивление [Ом]
t — время [c]
То есть в данном случае формула КПД будет иметь вид:
η = Q/A *100% = Q/UIt *100%
Переводим минуты в секунды — 2 минуты = 120 секунд. Теперь намм известны все значения, поэтому подставим их:
η = 22176/220*1,4*120 *100% = 60%
Ответ: КПД чайника равен 60%.
Давайте выведем еще одну формулу для КПД, которая часто пригождается для электрических цепей, но применима ко всему. Для этого нужна формула работы через мощность:
Работа электрического тока A = Pt A — работа электрического тока [Дж] P — мощность [Вт] t — время [c] |
Подставим эту формулу в числитель и в знаменатель, учитывая, что мощность разная — полезная и затраченная. Поскольку мы всегда говорим об одном процессе, то есть полезная и затраченная работа ограничены одним и тем же промежутком времени, можно сократить время и получить формулу КПД через мощность.
КПД η = Pполезная/Pзатраченная *100% η — коэффициент полезного действия [%] Pполезная — полезная мощность [Дж] Pзатраченная — затраченная мощность [Дж] |
Физическая формула КПД
Существует определенная формула для нахождения КПД. Она звучит следующим образом: чтобы найти КПД в физике, нужно количество энергии разделить на проделанную системой работу. То есть КПД — это отношение затраченной энергии к выполненной работе. Отсюда можно сделать простой вывод, что тем лучше и эффективнее система или тело, чем меньше энергии затрачивается на выполнение работы.
Сама формула выглядит кратко и очень просто Ƞ будет равняться A/Q. То есть Ƞ = A/Q. В этой краткой формулы и фиксируют нужные нам элементы для вычисления. То есть A в этом случае является использованной энергией, которая потребляется системой во время работы, а большая буква Q, в свою очередь, будет являться затраченной A, или опять же затраченной энергией.
В идеале КПД равен единице. Но, как это обычно бывает, он её меньше. Так происходит по причине физики и по причине, конечно же, закона о сохранении энергии.
Все дело в том, что закон сохранения энергии предполагает, что не может быть получено больше А, чем получено энергии. И даже единице этот коэффициент будет равняться крайне редко, поскольку энергия тратится всегда. И работа сопровождается потерями: к примеру, у двигателя потеря заключается в его обильном нагреве.
Итак, формула КПД:
Ƞ=А/Q, где
- A — полезная работа, которую выполняет система.
- Q — энергия, которую потребляет система.
Применение в разных сферах физики
Примечательно, что КПД не существует как понятие нейтральное, для каждого процесса есть свой КПД, это не сила трения, он не может существовать сам по себе.
Рассмотрим несколько из примеров процессов с наличием КПД.
К примеру, возьмем электрический двигатель.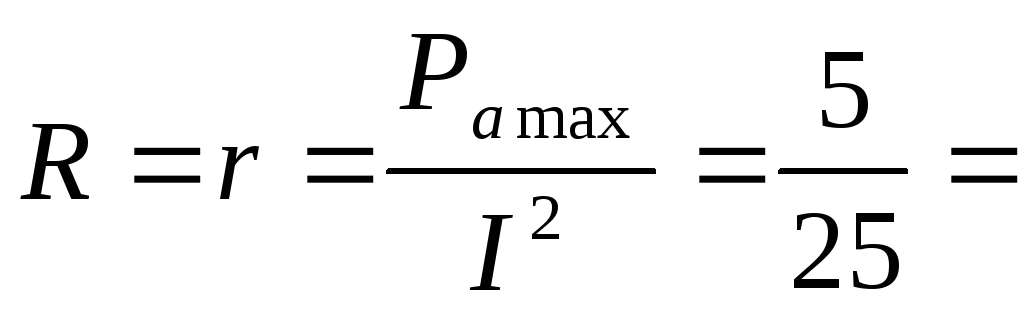 Задача электрического двигателя — преобразовывать электрическую энергию в механическую. В этом случае коэффициентом будет являться эффективность двигателя в отношении преобразования электроэнергии в энергию механическую. Для этого случая также существует формула, и выглядит она следующим образом: Ƞ=P2/P1. Здесь P1 — это мощность в общем варианте, а P2 — полезная мощность, которую вырабатывает сам двигатель.
Задача электрического двигателя — преобразовывать электрическую энергию в механическую. В этом случае коэффициентом будет являться эффективность двигателя в отношении преобразования электроэнергии в энергию механическую. Для этого случая также существует формула, и выглядит она следующим образом: Ƞ=P2/P1. Здесь P1 — это мощность в общем варианте, а P2 — полезная мощность, которую вырабатывает сам двигатель.
Нетрудно догадаться что структура формулы коэффициента всегда сохраняется, меняются в ней лишь данные, которые нужно подставить. Они зависят от конкретного случая, если это двигатель, как в случае выше, то необходимо оперировать затрачиваемой мощностью, если работа, то исходная формула будет другая.
Теперь мы знаем определение КПД и имеем представление об этом физическом понятии, а также об отдельных его элементах и нюансах. Физика — это одна из самых масштабных наук, но её можно разобрать на маленькие кусочки, чтобы понять. Сегодня мы исследовали один из этих кусочков.
Видео
Это видео поможет вам понять, что такое КПД.
Как устроен тепловой двигатель
Любой тепловой двигатель состоит из трех основных частей:
- рабочего тела;
- нагревателя;
- холодильника.
В основе работы двигателя лежит циклический процесс.
Нагреватель с помощью, например, сгорания топливной смеси выделяет большое количество теплоты и передает ее рабочему телу.
Рабочее тело, например пар, газ или жидкость, при нагревании расширяется и совершает работу, к примеру, вращает турбину или перемещает поршень.
Холодильник нужен, чтобы вернуть рабочее тело в начальное состояние. Он поглощает часть энергии рабочего тела. Таким образом обеспечивается цикличность, и тепловой двигатель работает непрерывно.
Идеальный тепловой двигатель Карно
Модель двигателя Карно разработал французский физик С. Карно.
Карно.
Рабочая часть двигателя Карно — поршень в заполненном газом цилиндре. Двигатель Карно — идеальная машина, она возможна только в теории. Поэтому в ней силы трения между поршнем и цилиндром и тепловые потери считаются равными нулю.
Механическая работа максимальна, если рабочее тело выполняет цикл, состоящий из двух изотерм и двух адиабат. При изотермическом расширении работа газа совершается за счет внутренней энергии нагревателя. При адиабатном процессе — за счет внутренней энергии расширяющегося газа. В этом цикле нет контакта тел с разной температурой, поэтому исключена теплопередача без совершения работы. Такой цикл называют циклом Карно.
Адиабатический процесс — это термодинамический процесс, происходящий без теплообмена с окружающей средой (Q=0).
Изотермический процесс — это термодинамический процесс, происходящий при постоянной температуре. Так как у идеального газа внутренняя энергия зависит только от температуры, то переданное газу количество тепла Q идет полностью на совершение работы A (Q=A).
Функционирует двигатель Карно следующим образом:
- Цилиндр вступает в контакт с горячим резервуаром, и газ расширяется при постоянной температуре. На этой фазе газ получает от горячего резервуара тепло.
- Цилиндр окружается теплоизоляцией, за счет чего количество тепла, имеющееся у газа, сохраняется. Газ продолжает расширяться, пока его температура не упадет до температуры холодного теплового резервуара.
- На третьей фазе теплоизоляция снимается. Газ в цилиндре, будучи в контакте с холодным резервуаром, сжимается, отдавая при этом часть тепла холодному резервуару.
- Когда сжатие достигает определенной точки, цилиндр снова окружается теплоизоляцией. Газ сжимается за счет поднятия поршня до тех пор, пока его температура не сравняется с температурой горячего резервуара. После этого теплоизоляция удаляется, и цикл повторяется вновь с первой фазы.
Примечание
Чем больше разница между температурами нагревателя и холодильника, тем больше КПД двигателя Карно.
Трактовка понятия
Электродвигатель и другие механизмы выполняют определённую работу, которая называется полезной. Устройство, функционируя, частично растрачивает энергию. Для определения эффективности работы применяется формула ɳ= А1/А2×100%, где:
- А1 — полезная работу, которую выполняет машина либо мотор;
- А2 — общий цикл работы;
- η – обозначение КПД.
Показатель измеряется в процентах. Для нахождения коэффициента в математике используется следующая формула: η= А/Q, где А — энергия либо полезная работа, а Q — затраченная энергия. Чтобы выразить значение в процентах, КПД умножается на 100%. Действие не несёт содержательного смысла, так как 100% = 1. Для источника тока КПД меньше единицы.
В старших классах ученики решают задачи, в которых нужно найти КПД тепловых двигателей. Понятие трактуется следующим образом: отношение выполненной работы силового агрегата к энергии, полученной от нагревателя. Расчет производится по следующей формуле: η= (Q1-Q2)/Q1, где:
- Q1 — теплота, полученная от нагревательного элемента;
- Q2 — теплота, отданная холодильной установке.

Максимальное значение показателя характерно для циклической машины. Она оперирует при заданных температурах нагревательного элемента (Т1) и холодильника (Т2). Измерение осуществляется по формуле: η= (Т1-Т2)/Т1. Чтобы узнать КПД котла, который функционирует на органическом топливе, используется низшая теплота сгорания.
Плюс теплового насоса как нагревательного прибора заключается в возможности получать больше энергии, чем он может затратить на функционирование. Показатель трансформации вычисляется путём деления тепла конденсации на работу, затрачиваемую на выполнение данного процесса.
Коэффициент полезного действия — FINDOUT.SU
Поможем в ✍️ написании учебной работы
Имя
Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой
Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно — исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое
Нажимая кнопку «Продолжить», я принимаю политику конфиденциальности
Каждая машина и механизм, совершая работу, тратит часть энергии на преодоление вредных сопротивлений.
Таким образом, машина (механизм) кроме полезной работы совершает еще и дополнительную работу.
Отношение полезной работы к полной работе или полезной мощности ко всей затраченной мощности называется коэффициентом полезного действия (КПД):
Полезная работа (мощность) расходуется на движение с заданной скоростью и определяется по формулам:
Тема 1.14. Работа и мощность. КПД 117
Затраченная мощность больше полезной на величину мощности, идущей на преодоление трения в звеньях машины, на утечки и тому подобные потери.
Чем выше КПД, тем совершеннее машина.
Примеры решения задач
Пример 1. Определить потребную мощность мотора лебедки для подъема груза весом 3 кН на высоту 10 м за 2,5 с (рис. 16.3). КПД механизма лебедки 0,75.
Решение
1. Мощность мотора используется на подъем груза с заданной скоростью и преодоление вредных сопротивлений механизма лебедки.
Мощность мотора используется на подъем груза с заданной скоростью и преодоление вредных сопротивлений механизма лебедки.
Полезная мощность определяется по формуле Р = Fvcosα. В данном случае α = 0; груз движется поступательно.
S 10
2. Скорость подъема груза v = —; v = — = 4 м/с.
T 2,5
3. Необходимое усилие равно весу груза (равномерный подъем).
4. Полезная мощность Р = 3000 ∙ 4 = 12 000 Вт.
5. Полная мощность, затрачиваемая мотором,
Пример 2. Судно движется со скоростью 56 км/ч (рис. 16.4). Двигатель развивает мощность 1200 кВт. Определить силу сопротивления воды движению судна. КПД машины 0,4.
Решение
1. Определяем полезную мощность, используемую на движение с заданной скоростью:
118 Лекция 16
2. По формуле для полезной мощности можно определить движущую силу судна с учетом условия α = 0. При равномерном движении движущая сила равна силе сопротивления воды: F дв = Fconp .
По формуле для полезной мощности можно определить движущую силу судна с учетом условия α = 0. При равномерном движении движущая сила равна силе сопротивления воды: F дв = Fconp .
Сила сопротивления воды движению судна Fсопр = 48 кН.
Пример 3. Точильный камень прижимается к обрабатываемой детали с силой 1,5 кН (рис. 16.5). Какая мощность затрачивается на обработку детали, если коэффициент трения материала камня о деталь 0,28; деталь вращается со скоростью 100 об/мин, диаметр детали 60 мм.
Решение
1. Резание осуществляется за счет трения между точильным камнем и обрабатываемой деталью:
3. Угловая скорость вращения детали
4. Мощность, необходимая для обработки детали:
Контрольные вопросы и задания
1. Запишите формулы для расчета работы при поступательном и вращательном движениях.
Тема 1.14. Работа и мощность. КПД 119
2. Вагон массой 1000 кг перемещают по горизонтальному пути
на 5 м, коэффициент трения 0,15. Определите работу силы тяжести.
3. Колодочным тормозом останавливают барабан после отключения двигателя (рис. 16.6). Определите работу торможения за 3 оборота, если сила прижатия колодок к барабану 1 кН, коэффициент трения 0,3.
4. Натяжение ветвей ременной передачи S 1 = 700 Н, S2 = 300 Н
(рис. 16.7). Определите вращающий момент передачи.
5. Запишите формулы для расчета мощности при поступательном и вращательном движениях.
6. Определите мощность, необходимую для подъема груза весом 0,5 кН на высоту 10 м за 1 мин.
7. Определите общий КПД механизма, если при мощности двигателя 12,5 кВт и общей силе сопротивления движению 2 кН скорость движения 5 м/с.
8. Ответьте на вопросы тестового задания.
Тема 1. 14. Динамика.
14. Динамика.
Работа и мощность
120 Лекция 16
Тема 1.15. Общие теоремы динамики 121
ЛЕКЦИЯ 17
Тема 1.15. Общие теоремы динамики
Иметь представление о понятиях «импульс силы», «количество движения», «кинетическая энергия»; о системе материальных точек, о внутренних и внешних силах системы.
Знать основные теоремы динамики, основные уравнения динамики при поступательном и вращательном движениях твердого тела, формулы для расчета моментов инерции некоторых однородных твердых тел.
Уметь определять параметры движения с помощью теорем динамики.
Теорема об изменении количества движения
Количеством движения материальной точки называется векторная величина, равная произведению массы точки на ее скорость mv .
Вектор количества движения совпадает по направлению с вектором скорости. Единица измерения [ mv ] — кг∙м/с.
Произведение постоянного вектора силы на некоторый промежуток времени, в течение которого действует эта сила, называется импульсом силы Ft .
Вектор импульса силы по направлению совпадает с вектором силы.
Использовав основное уравнение динамики, после преобразования можно получить соотношение между количеством движения и импульсом силы (рис. 17.1).
122 Лекция 17
Полученное соотношение выражает теорему об изменении количества движения точки:
Изменение количества движения точки за некоторый промежуток времени равно импульсу силы, действующему на точку в течение того же промежутка времени.
Теорема об изменении кинетической энергии
Энергией называется способность тела совершать механическую работу.
Существуют две формы механической энергии: потенциальная энергия, или энергия положения, и кинетическая энергия, или энергия движения.
Потенциальная энергия (П) определяет способность тела совершать работу при опускании с некоторой высоты до уровня моря. Потенциальная энергия численно равна работе силы тяжести.
П = Gh , где h — высота точки над уровнем моря.
Кинетическая энергия (К) определяется способностью движущегося тела совершать работу. Для материальной точки кинетическая энергия рассчитывается по формуле
Кинетическая энергия — величина скалярная, положительная.
Единицы измерения:
Энергия имеет размерность работы.
Запишем для материальной точки (рис. 17.2) основное уравнение движения
Спроектируем обе части векторного равенства на направление скорости:
Тема 1.15. Общие теоремы динамики 123
Умножив обе части полученного выражения на некоторое перемещение dS , получим:
Полученное равенство выражает теорему об изменении кинетической энергии точки:
Изменение кинетической энергии на некотором пути равно работе всех действующих на точку сил на том же пути.
Основы динамики системы материальных точек
Совокупность материальных точек, связанных между собой силами взаимодействия, называется механической системой.
Любое материальное тело в механике рассматривается как механическая система, образуемая совокупностью материальных точек.
Из определения механической системы следует, что движение каждой из точек, входящих в систему, зависит от движения остальных точек.
Силы, действующие на точки системы, делятся на внешние и внутренние. Силы взаимодействия между точками этой системы называют внутренними. К внешним силам относятся силы, действующие со стороны точек, не входящих в эту систему.
Примерами внешних сил являются сила тяжести, сила давления, сила трения и др.
К внутренним силам относятся силы упругости.
Движение механической системы зависит не только от внешних сил, но и от
n
суммарной массы системы m = ∑ Δ m k, где Δ m k — м асса отдельных точек
0
механической системы.
124 Лекция 17
Движение системы зависит и от положения центра масс системы — условной точки, в которой сосредоточена вся масса тела. Обычно считают, что в центре масс приложены все внешние силы.
Движение центра масс определяет движение всей системы только при поступательном движении, при котором все точки тела движутся одинаково.
Основное уравнение динамики при поступательном движении тела
Для определения движения тела (системы материальных точек) можно использовать второй закон динамики
где m — суммарная масса тела; ас— ускорение центра масс тела.
В поле земного притяжения центр масс совпадает с центром тяжести.
PLAN 2, Torque and Power
By Steven De Groote on
Введение
В моей первой книге я писал в основном о двигателях, особенно о высокоскоростных двигателях, производящих высокую удельную мощность, и в этом случае «удельной» была выходная мощность при заданной мощности двигателя или «лошадиная сила на литр мощности».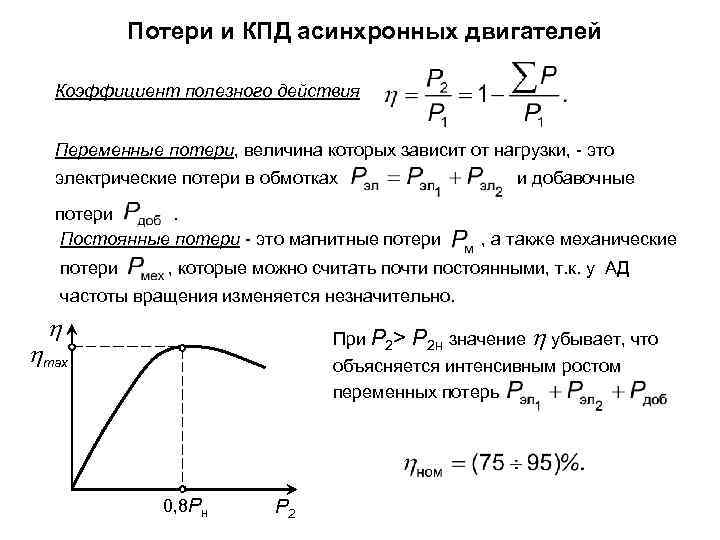 В этом повествовании на тему крутящего момента и мощности я более подробно рассмотрю динамику 4-х тактов типичного атмосферного двигателя.
В этом повествовании на тему крутящего момента и мощности я более подробно рассмотрю динамику 4-х тактов типичного атмосферного двигателя.
Вместимость в этой теме — это рабочий объем цилиндров, составляющих двигатель, и на них приходится A площадь поршня и L длина хода, которую на данный момент мы можем считать фиксированной. Это оставляет P и N в качестве двух других переменных для дальнейшего обсуждения, с которыми сейчас имеет дело I . Вопрос длины шатуна по отношению к радиусу кривошипа можно рассмотреть отдельно. Он не связан напрямую с общепризнанной формулой расчета лошадиных сил, но имеет некоторое влияние на выходную мощность двигателя.
ПЛАН относится к формуле для расчета лошадиных сил, где P представляет эффективное (среднее) давление в цилиндре во время рабочего хода. L и A — длина хода и площадь поршня. N — это скорость двигателя в оборотах в минуту (или секунду в некоторых формулах), и значения этих 4 переменных перемножаются. В моем первом повествовании я объяснил, что стиль письма был таким, чтобы дать понимание очень сложных вопросов тем, у кого есть искренний общий интерес, но с ограниченными техническими/математическими знаниями, и в то же время отважиться на высокотехнологичные вопросы с опытными техническими специалистами, где бы они ни находились. Я был подготовлен для этого. Общая цель заключалась в том, чтобы объединить понимание и обсуждение для людей из самых разных слоев общества, и я продолжаю придерживаться этого подхода.
В моем первом повествовании я объяснил, что стиль письма был таким, чтобы дать понимание очень сложных вопросов тем, у кого есть искренний общий интерес, но с ограниченными техническими/математическими знаниями, и в то же время отважиться на высокотехнологичные вопросы с опытными техническими специалистами, где бы они ни находились. Я был подготовлен для этого. Общая цель заключалась в том, чтобы объединить понимание и обсуждение для людей из самых разных слоев общества, и я продолжаю придерживаться этого подхода.
Когда я учился, мне напомнили, что некоторые из нас мастера на все руки, а некоторые специалисты. Мои современники называли первых теми, кто очень мало знал о многих вещах, а вторых — теми, кто знал больше всего практически ни о чем. В конце концов, речь идет о командной работе, и мастер на все руки может стать катализатором, который может дать специалистам нестандартное мышление, чтобы они могли сосредоточиться и углубиться в него. Никто из нас не может быть всем во всех технических вопросах, но, как и в случае с двигателем, мы можем настроить наши знания на максимум там, где это необходимо, в то же время сохраняя широкую кривую мощности или перспективу, чтобы охватить целый ряд вопросов.
В этом кратком повествовании я хочу исследовать вопрос о крутящем моменте и мощности. Крутящий момент напрямую связан с P, а крутящий момент, умноженный на скорость вращения, является способом расчета мощности или выполненной работы. При использовании PLAN выполненная работа рассчитывается путем умножения силы (давление X площадь) на расстояние, на котором эта сила действует (L, длина хода), умноженного на скорость, с которой это происходит, N.
Мощность двигателя зависит от энергии, содержащейся в топливе, которое он потребляет. Энергия топлива сжигается для выработки тепла, а двигатель преобразует это тепло в механическую энергию настолько эффективно, насколько это возможно. Эффективность теряется, когда часть тепла уходит через выхлопную трубу, а часть теряется из-за необходимости охлаждения двигателя. Имеются значительные потери на трение, в основном вызванные боковой силой трения поршня о стенку цилиндра, а также в других местах. Например, если клапаны двигателя приводятся в действие винтовыми пружинами, то сам процесс сжатия пружины вызывает нагрев самого материала пружины, а контакт между кулачком и толкателем кулачка будет выделять тепло.
Если та часть механической мощности от сгорания топлива, которая «теряется» из-за трения между поршнем и стенкой цилиндра, составляет 10 %, то механический КПД двигателя не может превышать 90 %. В 1963 году 3-литровый двигатель V12 потерял около 55 л.с. Для V8 это было бы около 52. Я не сомневаюсь, что за прошедшие полвека вопрос трения был хорошо изучен и что материалы, используемые в настоящее время, как физические компоненты, так и смазочные материалы, значительно снизили коэффициент трения. Эта «потеря» механической мощности возникает из-за того, что часть тепловой энергии остается в виде тепловой энергии, энергии, с которой мы не можем работать с пользой, но которую мы вынуждены выбрасывать в системах охлаждения, тем самым нагревая атмосферу вокруг себя. Энергия не может быть уничтожена, она существует постоянно в той или иной форме (каждое действие имеет равное и противоположное противодействие). Вообще говоря, топливо на 95 или 100 Octane содержат одинаковое количество энергии.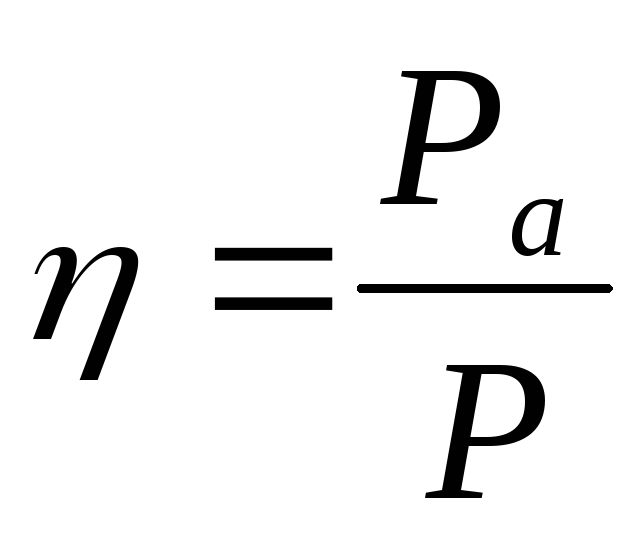 Проще говоря, октановое число относится к способности подавлять предварительное зажигание, чтобы повысить эффективность двигателя.
Проще говоря, октановое число относится к способности подавлять предварительное зажигание, чтобы повысить эффективность двигателя.
Я подтверждаю то, что я сказал в ПЛАН: «При заданном механическом КПД, чем быстрее двигатель может потреблять топливо, тем больше выходная мощность». Это было движущей целью, при которой в 1963 году была разработана конструкция узкоугольной 4-клапанной технологии. Эта конструкция камеры сгорания заменила полусферическую головку в качестве предпочтительной конструкции двигателей на следующие полвека.
Но механический КПД также варьируется не только в зависимости от конструкции и скорости двигателя, но и при различных настройках двигателя, и поэтому я продолжаю (как мастер на несколько профессий и начинающий специалист в нескольких интересующих меня областях) обсудите некоторые вещи, которые способствуют крутящему моменту и мощности.
Крутящий момент и мощность
Вопреки распространенному мнению, крутящий момент, создаваемый двигателем, не является постоянным на протяжении 360 градусов одного оборота и не является постоянным на протяжении 720 градусов четырехтактного двигателя.
Точно так же мощность, генерируемая за цикл из 4 тактов, непостоянна. Это может быть одинаковое количество для каждой последующей группы из 4 тактов, когда двигатель находится на постоянном дросселе и скорости, но участники форума говорили об ускорении, полученном за счет крутящего момента и мощности. И специалисты как бы отличались от универсалов (мастеров на все руки).
Крутящий момент (или механическое усилие) создается взрывной силой, создаваемой в цилиндре, за счет геометрии кривошипа и шатуна. Усилие, производящее мощность, приложенное к кривошипу, обычно прикладывается не на одной линии с цилиндром и не под прямым углом к углу кривошипа. Эти ситуации возникают только в ВМТ и НМТ и в двух случаях, когда шатун образует прямой угол с кривошипом. Эти два положения, в которых кривошип и шатун находятся под прямым углом, не совпадают, когда кривошип находится в положении 9.0 градусов, ни когда поршень находится на полпути своего хода, но изменен из-за геометрии длины шатуна и хода кривошипа.
В моей работе по проектированию Shell Twin в 1963 году (до электронных калькуляторов и задолго до компьютеров) я рассчитал силы, действующие внутри цилиндра в различных положениях вокруг 720 градусов, и нанес их на миллиметровую бумагу, чтобы измерения можно было проводить с позиций на кривые между каждым из положений, которые были измерены и рассчитаны.
При работе с этими силами необходимо понимать, что мощность в лошадиных силах (механическая мощность) рассчитывается путем умножения давления или нагрузки на поршень на пройденное расстояние. Таким образом, используемая шкала X представляет собой ход поршня. Также необходимо иметь шкалу X, показывающую относительный угол поворота коленчатого вала, чтобы определить нагрузки на шатун в виде векторов.
Две отдельные силы, действующие на группу поршень/шатун, давление газа и инерция, могут быть нанесены на график в одних и тех же терминах. Я выбрал эквивалентное давление газа, поэтому силы инерции, измеренные в фунтах усилия (масса, умноженная на ускорение), были преобразованы в давление газа путем деления на площадь поршня. Рабочее давление и силы инерции затем были нанесены на тот же график, шкала X в дюймах, шкала Y в фунтах на квадратный дюйм.
Рабочее давление и силы инерции затем были нанесены на тот же график, шкала X в дюймах, шкала Y в фунтах на квадратный дюйм.
Поскольку кривые относятся к одному и тому же измерению, силы можно суммировать, чтобы показать результирующую силу, действующую вдоль линии цилиндра. Отсюда, используя геометрию угла шатуна, силы, действующие на кривошип, и их направление можно отобразить на полярной диаграмме.
Графическое представление
Во-первых, я включил три грубо нарисованные диаграммы, A, B и C, которые показывают:
A – Силы инерции, которые одинаковы для всех 4 гребков, хотя и в двух разных направлениях
B – Давление газа на такте 2 и 3. Такты 1 и 4 по сравнению с ним практически нулевые.
C – Результирующие 4 хода при суммировании инерции и давления газа.
Приведенные выше ориентировочные кривые предназначены для облегчения интерпретации фактического графика 1A.
Боковая тяга
Боковая тяга теперь рассчитывается по приведенному выше графику с использованием сил, приложенных к геометрии, для получения следующей диаграммы.
При использовании этих шкал потери работы/мощности представляют собой площадь под кривыми, то есть давление (нагрузку), умноженное на пройденное расстояние и умноженное на коэффициент трения.
По мере увеличения скорости силы инерции и, следовательно, потери на трение увеличиваются на разность между квадратами скоростей.
Полярная диаграмма, нагрузка на большой конец
В моем примере, который следует ниже, полярная диаграмма имеет 24 положения кривошипа, каждое из которых смещается на 30 градусов, чтобы завершить 720 градусов 4-тактного цикла. 6 позиций для хода вниз и так далее.
На следующей диаграмме показаны 24 положения коленчатого вала, использованные при построении полярной диаграммы сил, действующих на шатунную шейку.
Эффективная нагрузка от давления, изображенная на полярной диаграмме, берется из шкалы Y на графике с использованием угла поворота кривошипа, показанного на шкале X. Эта сила нанесена под углом силы, приложенной к кривошипу через шатун от положения поршня, что также видно на графике. Из точек с 1 по 3 видно, что поршень сначала движется медленно, но проходит половину пути по отверстию, прежде чем кривошип достигает 90 градусов.
Из точек с 1 по 3 видно, что поршень сначала движется медленно, но проходит половину пути по отверстию, прежде чем кривошип достигает 90 градусов.
Следующая полярная диаграмма показывает фактический угол, под которым сила приложена большим концом шатуна к кривошипу при каждом из 24 углов кривошипа, принимая во внимание как направленную вниз силу поршня, так и боковую тягу со стороны кривошипа. боковая стенка цилиндра.
Мне не нужно было преобразовывать эти силы в крутящий момент. На этом этапе проектирования целью было определить нагрузки на подшипники и компоненты, и это можно было сделать, используя информацию, представленную в предыдущем материале.
Следующим этапом проектирования является применение данных ко всем шейкам двигателя и расчет нагрузок на коренные подшипники. Таким образом, аналогичным образом можно суммировать все силы, вызывающие нагрузку/крутящий момент. Это упражнение продемонстрирует, что создаваемый крутящий момент является очень неустойчивым и непостоянным в пределах 720 градусов одного цикла. Важен крутящий момент, измеряемый на выходе на маховик, на динамометре или на колесах.
Важен крутящий момент, измеряемый на выходе на маховик, на динамометре или на колесах.
Двигатель, для которого приведенный выше материал был конструктивными данными, представлял собой 3-литровый V 12, цилиндры которого были увеличены на 6% по сравнению с Shell Twin, а ход поршня увеличился примерно на 18% и составил 250 куб. см на цилиндр.
Несколько замечаний
1). Пока напряжения/нагрузки максимальны, работа не совершается без движения в ВМТ, точка 24, это просто мгновенное измерение. Работа связана с нагрузкой и движением. Сила, направленная вдоль цилиндра, не создает крутящего момента, хотя и создает его непосредственно перед и сразу после него.
2).Направление нагрузок – это линия между центром и контрольной точкой.
3).Величина нагрузки является мерой расстояния от центра до контрольной точки, шкала представляет собой круговые весы 2500 и 5000 фунтов.
4). Направление опорного вектора и угол поворота кривошипа не обязательно совпадают, опорная точка является одной из 24, изображенных выше, а вектор с тем же номером находится под показанным углом.
5). Кривая между точками 11 и 13, включая точки 12а и 12б, отражает значительное изменение давления при сжатии и воспламенении заряда. Кривая (линия) между 12а и 12b не будет производить механическую мощность, если это не позволяет геометрия шатуна и кривошипа. Позднее сгорание приведет к смещению точек 12а и 12b вправо от центра и повлияет на их значения. В то же время давление, продолжающееся после ВМТ, будет создавать увеличивающийся крутящий момент по мере увеличения угла поворота коленчатого вала. Эта кривая будет значительно изменять форму при изменении частоты вращения двигателя.
6). Давление в Shell Twin во время начальных испытаний было измерено со следующими основными данными:
- 1660 фунтов на кв. дюйм при 11 градусах ВМТ при 9500 об/мин
- 1360 фунтов на кв. дюйм при 15 градусах ВМТ при 10 000 об/мин
- 927 фунтов на кв. дюйм при 20 градусах ВМТ при 11 200 об/мин
- 820 фунтов на кв. дюйм при 30 градусах ВМТ при 11 400 об/мин
7). BMEP — Effective, Brake, что означает «Давление после учета потерь», трения, тепла и т. д.
BMEP — Effective, Brake, что означает «Давление после учета потерь», трения, тепла и т. д.
Я не могу здесь предоставить более полное отображение данных, подобных приведенным выше в таблице, с которыми можно работать, это усложняется из-за других переменных, таких как угол опережения зажигания , настройка впуска и выхлопа и т. д. Проект, над которым я работал, был выполнен с использованием очень раннего оборудования для мониторинга, ничего похожего на то, что доступно сегодня, но у меня есть данные о лошадиных силах, которые являются важной частью информации, необходимой для этого обсуждения.
Если рассматривать динамику во времени, то при 15 000 об/мин или 250 оборотов в секунду половина хода поршня занимает всего одну тысячную долю секунды, предел измерения времени в Гран-при. Я бы еще добавил, что этот мастер на все руки, ничего не смыслящий в датчиках холла, считает, что динамическое измерение крутящего момента на маховике, предложенное швалью, было бы делом для спецов, динамометр, или Тормоз как в БМЭП, кажется гораздо более спокойным и подходящим для меня.
На полярной диаграмме видно, что механическая мощность собирается между точками 13 и 17, а точка 15, вероятно, находится там, где крутящий момент будет максимальным в течение 720 градусов. Оптимизированное сгорание приведет к более высокому BMEP, улучшенному механическому КПД и меньшей мощности топлива, выкачиваемого из выхлопных труб. На следующем графике показано увеличение скорости на 25% с 10 до 12,5 тыс.
Крутящий момент/BMEP, об/мин и мощность
Кривые BMEP и Power для Shell Twin в мае 1965 года были такими, как показано здесь:
Показывает выходную мощность двигателя после периода развития плоской кривой крутящего момента/BMEP, отличной от пиковой мощности.
Этот конкретный график можно использовать для развития ваших аргументов о крутящем моменте и ускорении, тем более, что записанное BMEP/крутящий момент показывает незначительные пики при 7 и 10 тысячах оборотов в минуту и соответствующих мощностях от 35 до 50 лошадиных сил. Рост мощности между 9и 10 тысяч оборотов в минуту могут быть полезны для выхода автомобиля из поворота, в то время как продолжающееся увеличение мощности до 13 тысяч оборотов в минуту поможет разогнать автомобиль до возрастающего сопротивления воздуха и большего сцепления шин.
Этот двигатель развивал мощность 160 л.с. на литр в мае 1965 года, всего через полтора года после начала проекта с чистого листа. Он был рассчитан на 15 000 об/мин, но временно ограничен абсолютным максимумом в 13 000 об/мин, поскольку поршни были изготовлены из литого сплава, поковки в то время были за горизонтом, а литые поршни могли отделить материал над верхним кольцом из-за 7940 г напряжения в ВМТ.
Любые предложения «усилить» прочность этого участка материала вызовут связанное с этим увеличение требований к прочности во всех возвратно-поступательных частях, что приведет к общему снижению потенциала.
Текст и изображения Роя Франклина
Механика предыдущая | следующий
Эффективность двигателя
Эффективность двигателя
Ханну Яаскеляйнен
Это предварительный просмотр статьи, ограниченный некоторым исходным содержанием. Для полного доступа требуется подписка DieselNet.
Пожалуйста, войдите в систему , чтобы просмотреть полную версию этого документа.
Abstract : Преобразование энергии топлива в полезную работу в двигателе внутреннего сгорания сопряжено с рядом потерь. К ним относятся потери химической энергии с выбросами, потери тепла двигателем и через выхлопные газы, а также потери на перекачку газа и потери на трение в двигателе. Соответственно, общий тепловой КПД торможения двигателя является продуктом сгорания, термодинамического, газообменного и механического КПД.
- Потери энергии двигателя
- Сводка убытков
- Топливная энергия
- Эффективность сгорания
- Термодинамическая эффективность
- Тепловые потери
- Эффективность газообмена
- Механический КПД
- Эффективность с точки зрения топлива
Сводка потерь
Преобразование энергии топлива в полезную работу в двигателе внутреннего сгорания сопряжено с рядом потерь. Основные потери энергии двигателя и соответствующие коэффициенты эффективности показаны на рис. 1 9.0169 [3038] . Другие исследования факторов, влияющих на КПД двигателя, с акцентом на низкотемпературное сгорание, можно найти в литературе [4886] .
1 9.0169 [3038] . Другие исследования факторов, влияющих на КПД двигателя, с акцентом на низкотемпературное сгорание, можно найти в литературе [4886] .
Рисунок 1 . Обзор потерь энергии в типичном двигателе внутреннего сгорания
Начиная со сжигания углеводородного топлива и выделения его энергии, небольшое количество топлива не превращается полностью в идеальные продукты сгорания CO 2 и H 2 O. Энергия, остающаяся в несгоревшем топливе и промежуточных продуктах сгорания, равна приходится на эффективность сгорания .
Второй закон термодинамики определяет, что из энергии, высвобождаемой в процессе горения, только часть ее может быть преобразована в полезную работу. Эта доля объясняется термодинамическим КПД , который зависит от деталей цикла, используемого для преобразования тепла в работу. Для двигателей внутреннего сгорания верхний предел термодинамического КПД обычно определяют с помощью расчетов циклов Отто и Дизеля. Энергия сгорания, которая не преобразуется в механическую работу, теряется в виде тепла либо за счет выброса горячих выхлопных газов в окружающую среду, либо за счет передачи тепла через поверхности камеры сгорания. валовая указанная эффективность равна произведению эффективности сгорания и термодинамической эффективности и отражает общую работу, произведенную при сгорании топлива.
Энергия сгорания, которая не преобразуется в механическую работу, теряется в виде тепла либо за счет выброса горячих выхлопных газов в окружающую среду, либо за счет передачи тепла через поверхности камеры сгорания. валовая указанная эффективность равна произведению эффективности сгорания и термодинамической эффективности и отражает общую работу, произведенную при сгорании топлива.
Из энергии, которая была преобразована в работу, часть этой работы используется для подачи всасываемых газов в двигатель и вытеснения выхлопных газов. Эти насосные потери учитываются с помощью эффективности газообмена . Чистая указанная эффективность регулирует общую указанную эффективность с учетом работы, необходимой для перемещения газов в двигатель и из него.
Некоторая работа также должна быть использована для преодоления трения между скользящими поверхностями, такими как поршневые кольца и подшипники, и для привода необходимых вспомогательных устройств, таких как масляные насосы и насосы охлаждающей жидкости. Последнее учитывается с механическим КПД . Как ни странно, потери при газообмене и потери на трение иногда объединяются в одну потерю, которая используется для определения механического КПД. Это обсуждается ниже.
Последнее учитывается с механическим КПД . Как ни странно, потери при газообмене и потери на трение иногда объединяются в одну потерю, которая используется для определения механического КПД. Это обсуждается ниже.
Таким образом, оставшаяся работа, работа торможения, может быть получена от двигателя для выполнения полезной работы. Эффективность торможения (или термическая эффективность тормоза) может быть выражена как:
η тормоз = η сжигание · η термодинамический · η газообмен · η механический (1)
Еще один способ выразить эффективность торможения: [3980] :
.
η тормоз = η закрытый цикл · η открытый цикл · η механический
(2)
где:
η закрытый цикл – эффективность замкнутого цикла, причем закрытый цикл является частью 4-тактного цикла, когда впускной и выпускной клапаны закрыты. η закрытый цикл = η сгорание · η термодинамический
η открытый цикл — КПД открытого цикла, причем открытый цикл является частью 4-тактного цикла, когда впускной или выпускной клапаны открыты. η открытый цикл = η газообмен
η открытый цикл = η газообмен
Следует отметить, что это обсуждение КПД двигателя ведется с точки зрения процесса, используемого для преобразования тепла в работу, т. е. оно ограничено определенным типом машины и отражает ограничения машины или термодинамического цикла, используемого для преобразования тепла. работать. Эффективность также можно рассматривать с точки зрения топлива и количества топливной эксергии, которая может быть преобразована в работу. Более поздний подход, обсуждаемый позже, является более общим и не ограничивается каким-либо конкретным термодинамическим циклом.
Топливная энергия
В двигателе внутреннего сгорания воздух и топливо смешиваются, образуя горючую смесь, которая воспламеняется и выделяет энергию в виде тепла. Количество выделяемого тепла зависит от ряда факторов. В то время как количество топлива, попавшего в цилиндр, является основным фактором, определяющим содержание энергии в попавшей воздушно-топливной смеси и, следовательно, общее количество тепла, которое может быть выделено, ряд вторичных факторов также важен. Эти вторичные факторы включают детали о составе топлива, такие как тип элементов, содержащихся в топливе, и характер связей, соединяющих элементы вместе.
Эти вторичные факторы включают детали о составе топлива, такие как тип элементов, содержащихся в топливе, и характер связей, соединяющих элементы вместе.
Для двигателей чистая энергия, выделяемая при сгорании, обычно представлена низшей теплотворной способностью (LHV) топлива, поскольку предполагается, что вода, образующаяся при сгорании, остается в парообразном состоянии. На рис. 2 показана LHV ряда видов топлива, которые можно использовать в двигателе внутреннего сгорания, в зависимости от их стехиометрического соотношения воздух-топливо. Обратите внимание, что для углеводородного топлива значения LHV очень похожи и значительно выше, чем для топлива, содержащего кислород. Кислородсодержащие функциональные группы дают меньшую чистую энергию во время сгорания, внося значительный вклад в массу и объем топлива.
Рисунок 2 . Более низкая теплотворная способность (LHV) различных видов топлива по сравнению со стехиометрическим соотношением воздух-топливо
Данные с [391]
После того, как выбор топлива определен, мощность двигателя определяется содержанием энергии воздушно-топливной смеси, попавшей в цилиндр перед сгоранием. Для двигателей, в которых смешивание воздуха и топлива осуществляется до поступления всасываемого заряда в цилиндр, эта энергия связана с количеством воздушно-топливной смеси, которая может быть введена и захвачена в цилиндре. Для двигателей, в которых смешивание воздуха и топлива происходит в цилиндре после IVC, это зависит от количества воздуха, которое может быть введено и захвачено в цилиндре. Можно показать, что [4730] :
Для двигателей, в которых смешивание воздуха и топлива осуществляется до поступления всасываемого заряда в цилиндр, эта энергия связана с количеством воздушно-топливной смеси, которая может быть введена и захвачена в цилиндре. Для двигателей, в которых смешивание воздуха и топлива происходит в цилиндре после IVC, это зависит от количества воздуха, которое может быть введено и захвачено в цилиндре. Можно показать, что [4730] :
Hport=ρmixLHVfλ·AFRstoich+1H_port = {ρ_mix LHV_f} по {λ AFR_stoich +1}
(3)
где:
H порт = энергоемкость на единицу объема цилиндра смеси, образующейся до поступления в цилиндр, МДж/м 3
ρ смесь = плотность смеси, кг/м 3
LHV f = низшая теплота сгорания топлива, МДж/кг
λ = относительная воздушно-топливная смесь
AFR стех = стехиометрическая воздушно-топливная смесь
и
HDI=ρairLHVfλ·AFRstoichH_DI = {ρ_air LHV_f} над {λ AFR_stoich}
(4)
где:
H DI = энергоемкость единицы объема цилиндра смеси, образующейся в цилиндре после ВВК, МДж/м 3
ρ воздух = плотность воздуха, кг/м 3
Следует отметить, что для большинства жидких топлив разница между H порт и H DI невелика. Однако для газообразного топлива, такого как метан, основной компонент природного газа, разница может быть более существенной, рис. 3. Кроме того, в некоторых случаях, когда воздух и топливо смешиваются в цилиндре перед IVC, H порт больше отражает энергию, которая может быть захвачена в цилиндре. Влияние повышения давления на входе с помощью турбонагнетателя или нагнетателя в уравнении (3) и уравнении (4) учитывается через член плотности.
Однако для газообразного топлива, такого как метан, основной компонент природного газа, разница может быть более существенной, рис. 3. Кроме того, в некоторых случаях, когда воздух и топливо смешиваются в цилиндре перед IVC, H порт больше отражает энергию, которая может быть захвачена в цилиндре. Влияние повышения давления на входе с помощью турбонагнетателя или нагнетателя в уравнении (3) и уравнении (4) учитывается через член плотности.
Рисунок 3 . Энергия сгорания на единицу объема цилиндра смеси метана и воздуха в зависимости от λ
При 0°C, 101,325 кПа
На рис. 4 показаны значения H порта и H DI стехиометрических смесей нескольких видов топлива при стандартных условиях в зависимости от их стехиометрического соотношения воздух-топливо и на основе наиболее распространенных средств их смешивания с всасываемым воздухом 9.0169 [4730] . Хотя существуют важные различия, следует отметить, что выходная мощность двигателя, работающего на любом из этих видов топлива, исходя только из плотности энергии смеси, будет удивительно схожей. Однако следует отметить, что одной плотности энергии смеси недостаточно для определения максимальной мощности двигателя.
Однако следует отметить, что одной плотности энергии смеси недостаточно для определения максимальной мощности двигателя.
Рисунок 4 . Энергия сгорания на единицу объема цилиндра смеси топлива и воздуха при λ=1 в зависимости от стехиометрического соотношения воздух-топливо
При 0°C, 101,325 кПа
###
Мощность
Количественная работа связана с силой, вызывающей перемещение. Работа не имеет ничего общего с количеством времени, в течение которого эта сила действует, вызывая смещение. Иногда работа выполняется очень быстро, а иногда работа выполняется довольно медленно. Например, скалолазу требуется аномально много времени, чтобы поднять свое тело на несколько метров вверх по склону утеса. С другой стороны, турист (который выбирает более легкий путь в гору) может поднять свое тело на несколько метров за короткий промежуток времени. Два человека могут выполнить один и тот же объем работы, но турист сделает ее за значительно меньшее время, чем скалолаз. Величина, связанная со скоростью, с которой выполняется определенный объем работы, называется мощностью. У туриста больше номинальная мощность , чем скалолаз.
Величина, связанная со скоростью, с которой выполняется определенный объем работы, называется мощностью. У туриста больше номинальная мощность , чем скалолаз.
Мощность — это скорость выполнения работы. Это соотношение работа/время. Математически это вычисляется с использованием следующего уравнения.
или
P = Вт / т
Стандартной метрической единицей мощности является Вт . Как следует из уравнения мощности, единица мощности эквивалентна единице работы, деленной на единицу времени. Таким образом, ватт эквивалентен джоулю в секунду. По историческим причинам л.с. иногда используется для описания мощности, выдаваемой машиной. Одна лошадиная сила эквивалентна примерно 750 Вт.
Большинство машин спроектированы и изготовлены для работы с объектами. Все машины обычно описываются номинальной мощностью. Номинальная мощность указывает скорость, с которой эта машина может работать с другими объектами. Таким образом, мощность машины — это отношение работы к времени для этой конкретной машины. Автомобильный двигатель является примером машины, которой присваивается номинальная мощность. Номинальная мощность относится к тому, насколько быстро автомобиль может разогнать автомобиль. Предположим, что двигатель мощностью 40 лошадиных сил может разогнать автомобиль с 0 до 60 миль/ч за 16 секунд. Если бы это было так, то автомобиль, мощность которого в четыре раза превышала бы мощность, мог бы выполнить тот же объем работы за четверть времени. То есть 160-сильный двигатель мог разогнать тот же автомобиль с 0 до 60 миль/ч за 4 секунды. Дело в том, что при одном и том же объеме работы мощность и время обратно пропорциональны. Уравнение мощности предполагает, что более мощный двигатель может выполнить тот же объем работы за меньшее время.
Таким образом, мощность машины — это отношение работы к времени для этой конкретной машины. Автомобильный двигатель является примером машины, которой присваивается номинальная мощность. Номинальная мощность относится к тому, насколько быстро автомобиль может разогнать автомобиль. Предположим, что двигатель мощностью 40 лошадиных сил может разогнать автомобиль с 0 до 60 миль/ч за 16 секунд. Если бы это было так, то автомобиль, мощность которого в четыре раза превышала бы мощность, мог бы выполнить тот же объем работы за четверть времени. То есть 160-сильный двигатель мог разогнать тот же автомобиль с 0 до 60 миль/ч за 4 секунды. Дело в том, что при одном и том же объеме работы мощность и время обратно пропорциональны. Уравнение мощности предполагает, что более мощный двигатель может выполнить тот же объем работы за меньшее время.
Человек также является машиной с номинальной мощностью . Некоторые люди обладают большей силой, чем другие. То есть некоторые люди способны выполнять тот же объем работы за меньшее время или больший объем работы за то же время. Обычная физическая лаборатория включает в себя быстрый подъем по лестнице и использование информации о массе, росте и времени для определения личной силы студента. Несмотря на диагональное движение по лестнице, часто предполагается, что горизонтальное движение является постоянным, и вся сила от ступеней используется для подъема ученика вверх с постоянной скоростью. Таким образом, вес ученика равен силе, совершающей работу над учеником, а высота лестницы — смещению вверх. Предположим, что Бен Пумпинирон поднимает свое 80-килограммовое тело по 2,0-метровой лестнице за 1,8 секунды. Если бы это было так, то мы могли бы вычислить 9 Бена.0181 номинальная мощность . Можно предположить, что Бен должен приложить к лестнице направленную вниз силу в 800 ньютонов, чтобы поднять свое тело. При этом лестница будет толкать тело Бена вверх с достаточной силой, чтобы поднять его тело вверх по лестнице. Также можно предположить, что угол между силой лестницы, действующей на Бена, и смещением Бена равен 0 градусов.
Обычная физическая лаборатория включает в себя быстрый подъем по лестнице и использование информации о массе, росте и времени для определения личной силы студента. Несмотря на диагональное движение по лестнице, часто предполагается, что горизонтальное движение является постоянным, и вся сила от ступеней используется для подъема ученика вверх с постоянной скоростью. Таким образом, вес ученика равен силе, совершающей работу над учеником, а высота лестницы — смещению вверх. Предположим, что Бен Пумпинирон поднимает свое 80-килограммовое тело по 2,0-метровой лестнице за 1,8 секунды. Если бы это было так, то мы могли бы вычислить 9 Бена.0181 номинальная мощность . Можно предположить, что Бен должен приложить к лестнице направленную вниз силу в 800 ньютонов, чтобы поднять свое тело. При этом лестница будет толкать тело Бена вверх с достаточной силой, чтобы поднять его тело вверх по лестнице. Также можно предположить, что угол между силой лестницы, действующей на Бена, и смещением Бена равен 0 градусов.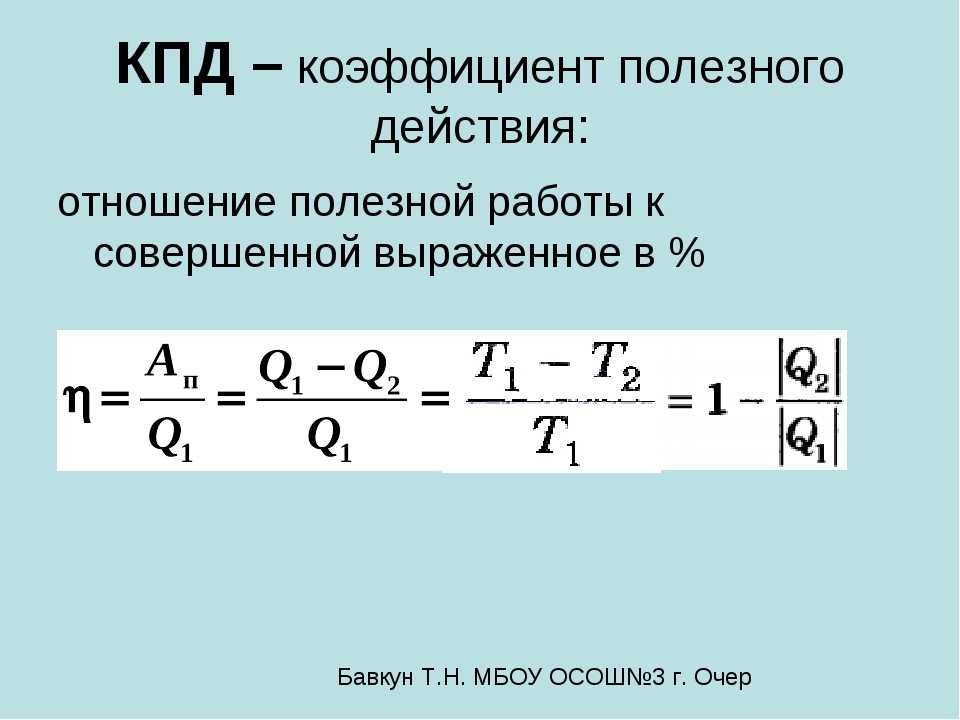 С этими двумя приближениями номинальная мощность Бена может быть определена, как показано ниже.
С этими двумя приближениями номинальная мощность Бена может быть определена, как показано ниже.
Мощность Бена составляет 871 Вт. Он довольно лошадь .
Другая формула мощности
Выражением мощности является работа/время. А поскольку выражение для работы есть сила*смещение, выражение для мощности можно переписать как (сила*смещение)/время. Поскольку выражение для скорости есть перемещение/время, выражение для мощности можно еще раз переписать как сила*скорость. Это показано ниже.
Это новое уравнение для мощности показывает, что мощная машина одновременно мощная (большая сила) и быстрая (большая скорость). Мощный автомобильный двигатель силен и быстр. Мощная сельскохозяйственная техника надежна и быстра. Мощный тяжелоатлет силен и быстр. Сильный лайнсмен в футбольной команде силен и быстр. А 9Машина 0181 , которая достаточно мощна, чтобы приложить большую силу, чтобы вызвать перемещение за небольшой промежуток времени (т. е. с большой скоростью), является мощной машиной.
е. с большой скоростью), является мощной машиной.
Проверьте свое понимание
Используйте свое понимание работы и мощности, чтобы ответить на следующие вопросы. Когда закончите, нажмите кнопку, чтобы просмотреть ответы.
1. Два студента-физика, Уилл Н. Эндэйбл и Бен Пампинирон, в зале тяжелой атлетики. Уилл поднимает над головой 100-фунтовую штангу 10 раз за одну минуту; Бен поднимает 100-фунтовую штангу над головой 10 раз за 10 секунд. Кто из учеников больше всего работает? ______________ Кто из учеников проявляет наибольшую силу? ______________ Объясните свои ответы.
2. Во время физического кабинета Джек и Джилл взбежали на холм. Джек вдвое массивнее Джилл; однако Джилл преодолевает то же расстояние вдвое быстрее. Кто работал больше всех? ______________ Кто приложил больше всего усилий? ______________ Объясните свои ответы.
3. Уставшая белка (массой около 1 кг) отжимается, прикладывая силу, поднимающую ее центр масс на 5 см, чтобы совершить работу всего лишь в 0,50 Дж. Если усталая белка проделает всю эту работу за 2 секунды, то определите ее мощность.
4. Подтягиваясь , студент-физик поднимает свое тело массой 42,0 кг на расстояние 0,25 метра за 2 секунды. Какую силу развивают бицепсы студента?
5. Ежемесячный счет за электричество в вашей семье часто выражается в киловатт-часах. Один киловатт-час – это количество энергии, отдаваемое потоком 1 киловатт электроэнергии за один час. Используйте коэффициенты преобразования, чтобы показать, сколько джоулей энергии вы получаете, когда покупаете 1 киловатт-час электроэнергии.
6. Эскалатор используется для перемещения 20 пассажиров каждую минуту с первого этажа универмага на второй. Второй этаж расположен на 5,20 м выше первого этажа. Средняя масса пассажира 54,9 кг. Определить мощность эскалатора, необходимую для перемещения такого количества пассажиров за это время.
Второй этаж расположен на 5,20 м выше первого этажа. Средняя масса пассажира 54,9 кг. Определить мощность эскалатора, необходимую для перемещения такого количества пассажиров за это время.
Перейти к следующему уроку:
Двигатель внутреннего сгорания в сравнении с газовой турбиной — скорость изменения скорости
Гибкость электростанции признана жизненно важным инструментом для управления изменчивостью электрических нагрузок и предоставления услуг по поддержке сети. Одним из показателей этой гибкости является скорость линейного изменения — скорость, с которой электростанция может увеличивать или уменьшать мощность. Двигатели Wärtsilä могут развивать скорость более 100 % в минуту, что намного быстрее, чем газовые турбины, обеспечивая сверхбыструю мощность, необходимую для интеграции возобновляемых источников энергии.
Гибкие генераторные установки помогают обеспечить стабильность электросети, увеличивая или уменьшая мощность при изменении спроса и нагрузки системы. Поскольку генерация солнечной и ветровой энергии может измениться в течение нескольких минут, операторы электросетей полагаются на электростанции, которые могут обеспечить дополнительную нагрузку (или снизить нагрузку) в том же временном масштабе, что и изменения в мощности возобновляемых источников. Увеличение или уменьшение производительности в минуту в режиме вращения называется скоростью изменения скорости и обычно выражается либо в % в минуту, либо в МВт в минуту.
Поскольку генерация солнечной и ветровой энергии может измениться в течение нескольких минут, операторы электросетей полагаются на электростанции, которые могут обеспечить дополнительную нагрузку (или снизить нагрузку) в том же временном масштабе, что и изменения в мощности возобновляемых источников. Увеличение или уменьшение производительности в минуту в режиме вращения называется скоростью изменения скорости и обычно выражается либо в % в минуту, либо в МВт в минуту.
Скорость изменения скорости вращения большинства моделей газовых турбин с промышленной рамой составляет около 20 % в минуту и около 50 % в минуту для авиационных газовых турбин. Для газовых турбин с комбинированным циклом типичная скорость линейного изменения составляет около 10 % в минуту. В качестве альтернативы скорость линейного изменения иногда выражается в МВт/минуту. Скорость линейного изменения зависит от мощности энергоблока, условий эксплуатации (будь то блок только запускается или работает в точке удержания минимальной нагрузки) и дополнительных технологий для сокращения времени запуска и увеличения скорости линейного изменения. Скорость нарастания мощности электростанции также зависит от количества агрегатов и конфигурации. Например, скорость изменения скорости 110 МВт/мин основана на проектах многотурбинных установок с большой единичной мощностью, , такой как парогазовая установка с комбинированным циклом (ПГУ) (полезная выходная мощность 880 МВт), где каждая газовая турбина рассчитана на разгон до 55 МВт/мин. Хотя скорость нарастания в МВт/минуту является ценным показателем, важно понимать рабочие условия, при которых могут быть достигнуты заявленные скорости нарастания.
Скорость нарастания мощности электростанции также зависит от количества агрегатов и конфигурации. Например, скорость изменения скорости 110 МВт/мин основана на проектах многотурбинных установок с большой единичной мощностью, , такой как парогазовая установка с комбинированным циклом (ПГУ) (полезная выходная мощность 880 МВт), где каждая газовая турбина рассчитана на разгон до 55 МВт/мин. Хотя скорость нарастания в МВт/минуту является ценным показателем, важно понимать рабочие условия, при которых могут быть достигнуты заявленные скорости нарастания.
Пусковая нагрузочная способность в зависимости от скорости линейного изменения
Пусковая нагрузочная способность часто сильно отличается от рекламируемой скорости линейного изменения для газовых турбин. Скорости рампы газовой турбины обычно достижимы только после того, как установка достигла самоподдерживающейся скорости. Двигатели внутреннего сгорания Wärtsilä обладают по-настоящему быстрым запуском, достигая полной нагрузки в течение 2 минут после команды запуска.
Пусковая нагрузка электростанций Wärtsilä и типичных газовых турбин сравнивается на рис. 1. Быстрое время запуска двигателей Wärtsilä обеспечивает значительное эксплуатационное преимущество по сравнению с газовыми турбинами. Поскольку газовые турбины только вырабатывают мощность, обе электростанции Wärtsilä уже вышли на полную мощность.
Факторы, влияющие на скорость линейного изменения мощности ПГУ электростанции
Скорость линейного изменения мощности ПГУ ограничена для предотвращения термического напряжения в компонентах парогенератора-утилизатора (HRSG) и паровой турбины. В обычных парогазовых установках газовая турбина плавно изменяется до точек удержания (где газовая турбина удерживается при постоянной нагрузке), чтобы позволить температуре и давлению пара медленно повышаться в допустимых пределах материала. Особую озабоченность вызывают толстостенные компоненты, такие как паровой барабан высокого давления, которые могут испытывать термическую усталость при слишком быстром повышении температуры и давления. Однако недавние достижения ПГУ, включая улучшенную конструкцию котлов, байпасные системы для изоляции паровой турбины и пароохладители, которые поддерживают температуру пара в соответствующих пределах, позволяют газовой турбине работать независимо от паровой турбины. Такие технологии, как системы сжигания со сверхнизким выбросом NOx и резервный нагрев котла-утилизатора, используются для сокращения выбросов при линейном увеличении мощности. Эти улучшения привели к сокращению времени запуска и более высокой скорости изменения скорости, но такая быстрая цикличность влечет за собой увеличение затрат на техническое обслуживание ПГУ.
Однако недавние достижения ПГУ, включая улучшенную конструкцию котлов, байпасные системы для изоляции паровой турбины и пароохладители, которые поддерживают температуру пара в соответствующих пределах, позволяют газовой турбине работать независимо от паровой турбины. Такие технологии, как системы сжигания со сверхнизким выбросом NOx и резервный нагрев котла-утилизатора, используются для сокращения выбросов при линейном увеличении мощности. Эти улучшения привели к сокращению времени запуска и более высокой скорости изменения скорости, но такая быстрая цикличность влечет за собой увеличение затрат на техническое обслуживание ПГУ.
Фактический опыт эксплуатации
Электростанции Wärtsilä идеально подходят для работы в циклическом режиме, поскольку возможность быстрого увеличения и уменьшения нагрузки не влияет на график технического обслуживания. В дополнение к быстрому запуску двигатели Wärtsilä могут останавливаться в течение одной минуты и имеют более низкие выбросы благодаря технологии сжигания обедненной смеси. Даже в комбинированном цикле двигатели Wärtsilä сохраняют свою способность реагировать на нагрузку, поскольку паровая часть силовой установки рассчитана на низкие температуры и давления газа, которые можно поддерживать лишь при небольшом количестве работающих двигателей. Из-за модульная конструкция электростанций Wärtsilä , двигатели могут загружаться и разгружаться по отдельности, обеспечивая высокую эффективность установки даже при частичной нагрузке .
Даже в комбинированном цикле двигатели Wärtsilä сохраняют свою способность реагировать на нагрузку, поскольку паровая часть силовой установки рассчитана на низкие температуры и давления газа, которые можно поддерживать лишь при небольшом количестве работающих двигателей. Из-за модульная конструкция электростанций Wärtsilä , двигатели могут загружаться и разгружаться по отдельности, обеспечивая высокую эффективность установки даже при частичной нагрузке .
После запуска и при номинальных рабочих температурах электростанции Wärtsilä могут быстро увеличивать или уменьшать мощность. Электростанции Wärtsilä могут увеличивать нагрузку (или снижать) с 10 % до 100 % всего за 42 секунды, при этом эффективная рабочая скорость разгона превышает 100 % в минуту.
Разница в производительности газовых турбин и электростанций Wärtsilä очевидна на Рисунке 2, на котором представлен снимок экрана из реального диспетчерского центра в Колорадо, США. Wärtsilä 9Электростанция 0010 Plains End (красная и белая кривые нагрузки) использовалась для компенсации падения мощности ветра, быстрого запуска и выхода на полную нагрузку в течение нескольких минут. Напротив, газовые турбины (фиолетовая кривая нагрузки) разгонялись гораздо медленнее. Это иллюстрирует гибкость, обеспечиваемую электростанциями Wärtsilä, и подчеркивает, что стандартные показатели скорости разгона не всегда отражают эксплуатационные возможности.
Напротив, газовые турбины (фиолетовая кривая нагрузки) разгонялись гораздо медленнее. Это иллюстрирует гибкость, обеспечиваемую электростанциями Wärtsilä, и подчеркивает, что стандартные показатели скорости разгона не всегда отражают эксплуатационные возможности.
Рис. 2: На снимке экрана из диспетчерского центра показано снижение ветрогенерации (зеленая линия) и быстрый рост на Электростанция Wärtsilä’s Plains End для компенсации. По сравнению с быстрым линейным изменением мощности завода Wärtsilä мощность газовой турбины (фиолетовая линия) увеличивается медленнее.
лошадиных сил и крутящий момент: в чем разница?
Что лучше? Вот как можно подавить эти дебаты в барах.
Йоги Берра, никогда не останавливавшийся на деталях двигателя, пришел бы к выводу, что крутящий момент и мощность — это одно и то же, только разные. На самом деле, это упрощение частично верно.
Крутящий момент и мощность — это то, что производят двигатели, когда вы поворачиваете ключ и нажимаете на педаль акселератора. Воздух и топливо, воспламеняющиеся в камерах сгорания, заставляют коленчатый вал, трансмиссию и ведущие оси вращаться. Это чудо преобразования энергии: потенциальная энергия, содержащаяся в галлоне переработанного динозавра, эффективно преобразуется в кинетическую энергию, необходимую для движения.
Воздух и топливо, воспламеняющиеся в камерах сгорания, заставляют коленчатый вал, трансмиссию и ведущие оси вращаться. Это чудо преобразования энергии: потенциальная энергия, содержащаяся в галлоне переработанного динозавра, эффективно преобразуется в кинетическую энергию, необходимую для движения.
Копнув глубже, рассмотрите следующие определения из учебника:
Энергия — это способность выполнять работу. В этом случае двигатели выполняют тяжелую работу (работу), которую раньше выполняли лошади.
Работа является результатом действия силы на некотором расстоянии. Американская единица измерения работы (а также энергии) — футо-фунты. В Международной системе (СИ) работа измеряется в джоулях и, в редких случаях, в ньютон-метрах.
Крутящий момент — вращающая сила, создаваемая коленчатым валом двигателя. Чем больше крутящий момент выдает двигатель, тем больше его способность выполнять работу. Измерение такое же, как и работа, но немного другое. Поскольку крутящий момент представляет собой вектор (действующий в определенном направлении), он измеряется в фунтах-футах и ньютон-метрах.
Поскольку крутящий момент представляет собой вектор (действующий в определенном направлении), он измеряется в фунтах-футах и ньютон-метрах.
Конечно, всегда есть исключения. В этом случае разница заключается в статическом крутящем моменте , который вы применяете с помощью гаечного ключа, чтобы затянуть болты с головкой. Во избежание путаницы единицами измерения статического крутящего момента традиционно являются футо-фунты. Наоборот, система СИ использует ньютон-метры как для статических, так и для динамических измерений крутящего момента.
Мощность — это скорость выполнения работы. Шотландский изобретатель восемнадцатого века Джеймс Уатт дал нам эту удобную эквивалентность: одна лошадиная сила — это мощность, необходимая для того, чтобы поднять 33 000 фунтов ровно на один фут за одну минуту. В честь этого вклада единицей измерения мощности в системе СИ является киловатт.
Вернёмся к теореме Берра. Крутящий момент — это способность выполнять работу, а мощность — это скорость, с которой можно выполнить тяжёлую задачу. Другими словами, мощность — это скорость выполнения работы (или приложения крутящего момента) за заданный промежуток времени. Математически мощность равна крутящему моменту, умноженному на число оборотов в минуту. H = T x об/мин/5252, где H — мощность в лошадиных силах, T — фунт-фут, об/мин — скорость вращения двигателя, а 5252 — константа, заставляющая единицы измерения колебаться. Таким образом, чтобы увеличить мощность, двигатель должен генерировать больший крутящий момент, работать на более высоких оборотах или и то, и другое.
Другими словами, мощность — это скорость выполнения работы (или приложения крутящего момента) за заданный промежуток времени. Математически мощность равна крутящему моменту, умноженному на число оборотов в минуту. H = T x об/мин/5252, где H — мощность в лошадиных силах, T — фунт-фут, об/мин — скорость вращения двигателя, а 5252 — константа, заставляющая единицы измерения колебаться. Таким образом, чтобы увеличить мощность, двигатель должен генерировать больший крутящий момент, работать на более высоких оборотах или и то, и другое.
В то время как миниатюрные определения отлично подходят для учебников, их применение к реальным двигателям — совсем другое дело. Одна из проблем заключается в том, что у каждого автомобильного двигателя есть рабочий диапазон от холостого хода до красной черты. Например, 6,2-литровый V-8 Hellcat Dodge Challenger выдает 707 лошадиных сил ТОЛЬКО при 6000 об/мин. Он производит значительно меньше мощности на холостом ходу (достаточно только для вращения вспомогательного оборудования с приводом от двигателя) и чуть менее 700 лошадиных сил при красной черте 6200 об / мин. И он развивает свой максимальный крутящий момент в 650 фунт-футов ТОЛЬКО при 4000 об/мин.
И он развивает свой максимальный крутящий момент в 650 фунт-футов ТОЛЬКО при 4000 об/мин.
Другой проблемой является точное определение мощности и крутящего момента вращающегося коленчатого вала. Инструментом для этой задачи является динамометр двигателя. Хотя это слово означает «устройство измерения мощности», на практике измеряются крутящий момент и число оборотов двигателя, а его мощность рассчитывается по приведенной выше формуле.
Вихретоковые динамометры используют магнитное поле для передачи крутящего момента от вращающегося коленчатого вала к подшипнику рычага против датчика статической силы (известного как тензодатчик), расположенного на точном расстоянии от центра кривошипа. Другой широко используемый тип динамометра — водяной тормоз; он использует один вращающийся и один статический набор лопастей насоса для передачи крутящего момента коленчатого вала через плечо рычага на тензодатчик.
Идеальный двигатель развивает достаточный крутящий момент на низких оборотах и поддерживает его до красной отметки. Величина создаваемого крутящего момента прямо пропорциональна количеству воздуха, проходящего через двигатель. Большие двигатели перекачивают больше воздуха и, следовательно, создают больший крутящий момент. Бустеры — нагнетатели, турбокомпрессоры — подают дополнительный воздух, чтобы помочь маленьким двигателям действовать большими. Конечно, в камеры сгорания должно подаваться соответствующее количество топлива, но это несложно, особенно при впрыске с электронным управлением.
Величина создаваемого крутящего момента прямо пропорциональна количеству воздуха, проходящего через двигатель. Большие двигатели перекачивают больше воздуха и, следовательно, создают больший крутящий момент. Бустеры — нагнетатели, турбокомпрессоры — подают дополнительный воздух, чтобы помочь маленьким двигателям действовать большими. Конечно, в камеры сгорания должно подаваться соответствующее количество топлива, но это несложно, особенно при впрыске с электронным управлением.
Чтобы облегчить впрыск нужного количества топлива, конструкторы двигателей сталкиваются с рядом сложных задач. Один из них — сделать все компоненты достаточно прочными, чтобы выдерживать нагрузки, которым они подвергаются из-за давления сгорания, а в случае движущихся частей — из-за собственной инерции. Потребности в охлаждении и смазке примерно пропорциональны производимой мощности. А нагнетание воздуха в любой двигатель, через него и из него на сверхвысоких оборотах — это то, где инженерное дело становится искусством. Учтите топливную экономичность и чистоту выхлопа в уравнении разработки, и станет ясно, почему волшебники по двигателю редко тусуются у охладителя воды.
Учтите топливную экономичность и чистоту выхлопа в уравнении разработки, и станет ясно, почему волшебники по двигателю редко тусуются у охладителя воды.
К этому моменту обсуждения должно быть ясно, что крутящий момент и лошадиная сила подобны разлученным братьям и сестрам; они тесно связаны, но не имеют много общего. Но как насчет более серьезной моральной проблемы, стоящей перед человечеством в целом и перед автолюбителями в частности: что лучше?
Мы ответим так, как это оценил бы Йоги Берра. В бейсбольной игре, если крутящий момент аналогичен кетчеру, то лошадиная сила — это питчер. И то, и другое необходимо для игры в мяч, но обязанности питчера — определение скорости и траектории каждого брошенного мяча — определяют игру. Крутящий момент жизненно важен для работы любого двигателя, но мощность — это то, что отличает отличный двигатель от хорошего.
Этот контент импортирован из OpenWeb. Вы можете найти тот же контент в другом формате или найти дополнительную информацию на их веб-сайте.
Поправочный коэффициент Dyno и относительная мощность в лошадиных силах
Поправочный коэффициент Dyno и относительная мощность
Лошадиная сила
Так что же это за поправочный коэффициент?
Мощность и крутящий момент, доступные от внутреннего
двигатель внутреннего сгорания зависит от плотности воздуха… более высокая плотность
означает больше молекул кислорода и больше энергии… более низкая плотность означает меньше кислорода
и меньше мощность.
Относительная мощность и поправочный коэффициент динамометра позволяют математически
расчет влияния плотности воздуха на мощность при полностью открытой дроссельной заслонке
и крутящий момент. Поправочный коэффициент динамометрического стенда — это просто математическое
величина, обратная относительному значению лошадиных сил.
Первоначально все основные производители автомобилей в США находились в Детройте или его окрестностях, штат Мичиган, и показания динамометрического стенда, снятые в Детройте, считались стандартом. Однако, как
Однако, как
Автомобильная промышленность распространилась как по стране, так и по всему миру, автопроизводителям нужен был способ соотнести данные о мощности и крутящем моменте, полученные на этих «нестандартных» автомобилях.
локации с данными, взятыми в «стандартной» локации. Поэтому SAE создал J1349для того, чтобы преобразовать (или «исправить») данные динамометра, взятые, например,
в Калифорнии или в Токио, чтобы быть сопоставимыми с данными, полученными
в стандартных условиях в Детройте.
Для чего это нужно?
Поправочный коэффициент динамометрического стенда часто используется для стандартизации лошадиных сил.
и показания крутящего момента, так что влияние температуры окружающей среды и давления
удаляются из показаний. Используя поправочный коэффициент динамометра, мощность и
показания крутящего момента можно напрямую сравнить с показаниями, снятыми на некоторых других
день или даже на какой-то другой высоте.
То есть скорректированные показания совпадают с результатом, который вы бы получили
доведя автомобиль (или двигатель) до определенной контролируемой температуры, влажности
динамометрический цех с регулируемым давлением, где измеряют «стандарт»
мощность на основе тщательно контролируемой температуры, влажности и
давление.
Если вы отвезете свою машину на диностенде в холодный день на малой высоте, это заставит
много силы. И если вы возьмете точно такую же машину обратно на тот же динамометрический стенд на
жаркий день, это сделает меньше энергии. Но если взять точно такую же машину в
«стандартный» динамометрический стенд (где температура, влажность и давление тщательно
контролируемый) в эти разные дни, он всегда будет производить одинаковую мощность.
Иногда вам может понадобиться узнать, сколько энергии вы на самом деле зарабатываете на этом
конкретный день из-за температуры, влажности и давления в этот день; в
В этом случае вам следует посмотреть на нескорректированные показания мощности.
Но когда вы хотите увидеть, насколько больше у вас мощности исключительно за счет нового
коллекторы или новый кулачок, то вы обнаружите, что скорректированная мощность больше
полезно, так как устраняет влияние температуры, влажности и
атмосферное давление и просто показывает, насколько больше (или меньше) мощность у вас есть
чем в ваших предыдущих тестах.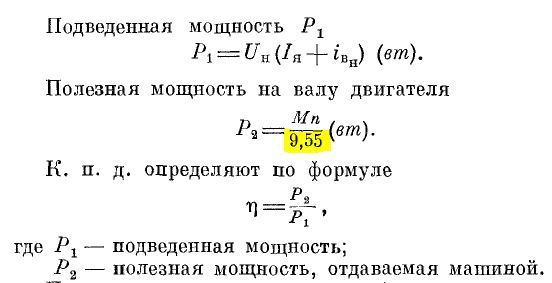
Нет «правильного» ответа… это просто вопрос того, как вы хотите использовать
Информация.
Если вы хотите знать, собираетесь ли вы сжечь транссексуал слишком много
мощности в прохладный влажный день, затем подойдите к динамометру и посмотрите на нескорректированную мощность, чтобы
посмотрите, сколько именно энергии у вас есть в этих условиях.
Но если вы хотите сравнить эффекты, вызванные модификациями, или вы хотите
сравнить несколько разных машин в разное время, потом скорректированные показания
«стандартный» дино будет полезнее.
Как это рассчитывается?
Общество автомобильных инженеров (SAE) разработало стандартный метод SAE J1349 JUN90 для
корректировка показаний мощности и крутящего момента, чтобы они выглядели так, как будто
все показания были сняты в одной и той же «стандартной» испытательной камере, где воздух
давление, влажность и температура воздуха поддерживаются постоянными. Кроме того,
Стандарт SAE J1349 JUN90 включает предполагаемый механический КПД 85%, чтобы обеспечить
оценка реальной мощности двигателя (без аксессуаров).
Уравнение для поправочного коэффициента динамометра, приведенное в SAE J1349 JUN90 (для
бензиновые двигатели с искровым зажиганием, работающие на полном газу (WOT),
в пересчете на давление в мб, составляет:
где: cf = коэффициент динамической коррекции
.
Pd = давление сухого воздуха, мб
Tc = температура окружающей среды, град C
Давление сухого воздуха Pd, находится путем вычитания давления пара Pv
от фактического давления воздуха. Для получения дополнительной информации о давлениях и
расчет давления пара, см. Воздух
Плотность и плотность высоты.
Относительная мощность — это просто математическая величина, обратная
поправочный коэффициент.
Обновление SAE J1349:
В августе 2004 г. SAE выпустила J1349, пересмотренный в августе 2004 г.
который указывает, что предпочтительный метод определения
мощность трения, используемая аксессуарами двигателя, является фактической
измерение, и что предположение о 85% механическом
эффективность (как ранее использовалось в SAE J1349 Revision JUN90) должна
использовать только тогда, когда фактические данные о трении недоступны.
Уравнение для расчета тормозной мощности (для искрового зажигания
бензиновые двигатели, работающие на полном газу (WOT), при условии, что 85%
механический КПД, был очень незначительно пересмотрен (и
представлено здесь в пересчете на использование давления в мб) как:
Раздел 5.1 SAE J1349, редакция от августа 2004 г., также разъясняет, что это исправление
фактор не предназначен для обеспечения точных поправок за
чрезвычайно широкий диапазон, а скорее, что предполагаемый диапазон воздуха
температура составляет от 15 до 35 ° C, а предполагаемый диапазон сухой
давление воздуха 9от 00 до 1050 мб.
Примечание. SAE J607 — это более старый стандарт, который не
попытка включить любое внутреннее трение двигателя
потери. Следовательно, J607 дает более высокие значения, которые не
включить потери на трение. SAE J1349 — это
более новый стандарт, который определяет различные способы включения
внутренние потери двигателя, и поэтому представляет собой более
точная индикация мощности двигателя.
Мощность и крутящий момент:
Мощность — это скорость выполнения работы. Когда крутящий момент двигателя поворачивается
коленчатый вал и мощность подаются, результирующая мощность может быть
выражается как:
, который можно упростить как
где: л.с. = лошадиная сила,
л.с.
t = крутящий момент, фут-фунт
об/мин = частота вращения двигателя, число оборотов в минуту
Это отличная формула. В основном это говорит о том, что если вы можете сохранить то же самое
количество крутящего момента, то чем больше оборотов вы можете крутить, тем больше лошадиных сил вы получаете!
Вот почему двигатели Formula One, CART и IRL развивают невероятные обороты.
чем быстрее вращается двигатель, тем больше мощности он может развить (если он правильно настроен на
работать на этой скорости).
Рассмотрим, например: двигатель внутреннего сгорания без наддува
обычно производит от 1 до 1,5 футо-фунтов крутящего момента на кубический дюйм, когда
должным образом настроены для работы на любых конкретных оборотах. С 2-литровым (около 122 кубических дюймов) двигателем, развивающим крутящий момент 1,5 фунта-фута на кубический дюйм, вы
С 2-литровым (около 122 кубических дюймов) двигателем, развивающим крутящий момент 1,5 фунта-фута на кубический дюйм, вы
ожидал получить около 180 л.с. при 5200 об/мин… но вы получите колоссальные 415
л.с., если вы можете заставить его работать на 12000 об/мин.
Сообщается, что 3,5-литровый двигатель IRL развивает мощность около 650 л.с. при 10 700 об/мин.
Это будет около 1,5 футо-фунтов на кубический дюйм при пиковых оборотах.
По слухам, 3,0-литровый двигатель Ferrari Formula One развивает мощность около 860 л.с.
при 18500 об/мин. Это было бы о
1,33 фут-фунта на кубический дюйм при пиковых оборотах.
Сообщается, что двигатель NASCAR Cup объемом 5,86 л производит
около 850 л.с. при 9000 об/мин, что примерно 1,39
ft-lbs на куб.
дюйм на пиковых оборотах.
Откровенно говоря, кажется, что эти нелепые значения оборотов — одна из
причины, по которым гонки CART, IRL и F1 так плохо воспринимаются
здесь, в США. Люди хотят видеть и слышать гоночные машины, которые они
могут идентифицировать себя с автомобилями, которые имеют что-то общее с
собственные автомобили зрителей, а не эти глупые маленькие моторы, которые звучат как
злые пчелы.
 Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.
Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.
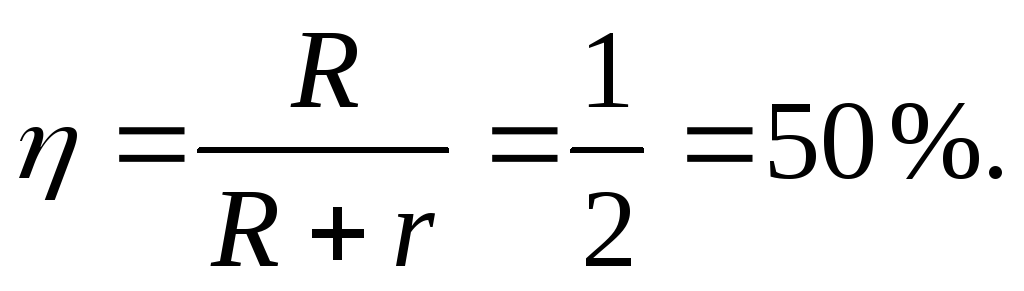 11. Работа и мощность тока
11. Работа и мощность тока = А полезн./t = I*U = I2*R;
= А полезн./t = I*U = I2*R; Определите внутреннее сопротивление аккумулятора.
Определите внутреннее сопротивление аккумулятора.
 4 КПД и его зависимость от нагрузки
4 КПД и его зависимость от нагрузки
