Содержание
§79. Характеристики асинхронных двигателей | Электротехника
Характеристики асинхронных двигателей.
Для правильной эксплуатации асинхронного двигателя необходимо знать его характеристики: механическую и рабочие.
Механическая характеристика.
Зависимость частоты вращения ротора от нагрузки (вращающегося момента на валу) называется механической характеристикой асинхронного двигателя (рис. 262, а). При номинальной нагрузке частота вращения для различных двигателей обычно составляет 98—92,5 % частоты вращения n1 (скольжение sном = 2 – 7,5 %). Чем больше нагрузка, т. е. вращающий момент, который должен развивать двигатель, тем меньше частота вращения ротора.
Как показывает кривая на рис. 262, а, частота вращения асинхронного двигателя лишь незначительно снижается при увеличении нагрузки в диапазоне от нуля до наибольшего ее значения. Поэтому говорят, что такой двигатель обладает жесткой механической характеристикой.
Наибольший вращающий момент Mmax двигатель развивает при некотором скольжении skp, составляющем 10—20%. Отношение Mmax/Mном определяет перегрузочную способность двигателя, а отношение Мп/Мном — его пусковые свойства.
Рис. 262. Механические характеристики асинхронного двигателя: а — естественная; б — при включении пускового реостата
Двигатель может устойчиво работать только при обеспечении саморегулирования, т. е. автоматическом установлении равновесия между приложенным к валу моментом нагрузки Мвн и моментом М, развиваемым двигателем. Этому условию соответствует верхняя часть характеристики до достижения Mmax (до точки В).
Если нагрузочный момент Мвн превысит момент Mmax, то двигатель теряет устойчивость и останавливается, при этом по обмоткам машины будет длительно проходить ток в 5—7 раз больше номинального, и они могут сгореть.
При включении в цепь обмоток ротора пускового реостата получаем семейство механических характеристик (рис. 262,б). Характеристика 1 при работе двигателя без пускового реостата называется естественной. Характеристики 2, 3 и 4, получаемые при подключении к обмотке ротора двигателя реостата с сопротивлениями R1п (кривая 2), R2п (кривая 3) и R3п (кривая 4), называют реостатными механическими характеристиками.
262,б). Характеристика 1 при работе двигателя без пускового реостата называется естественной. Характеристики 2, 3 и 4, получаемые при подключении к обмотке ротора двигателя реостата с сопротивлениями R1п (кривая 2), R2п (кривая 3) и R3п (кривая 4), называют реостатными механическими характеристиками.
При включении пускового реостата механическая характеристика становится более мягкой (более крутопадающей), так как увеличивается активное сопротивление цепи ротора R2 и возрастает sкp. При этом уменьшается пусковой ток. Пусковой момент Мп также зависит от R2. Можно так подобрать сопротивление реостата, чтобы пусковой момент Мп был равен наибольшему Мmax.
В двигателе с повышенным пусковым моментом естественная механическая характеристика приближается по своей форме к характеристике двигателя с включенным пусковым реостатом. Вращающий момент двигателя с двойной беличьей клеткой равен сумме двух моментов, создаваемых рабочей и пусковой клетками.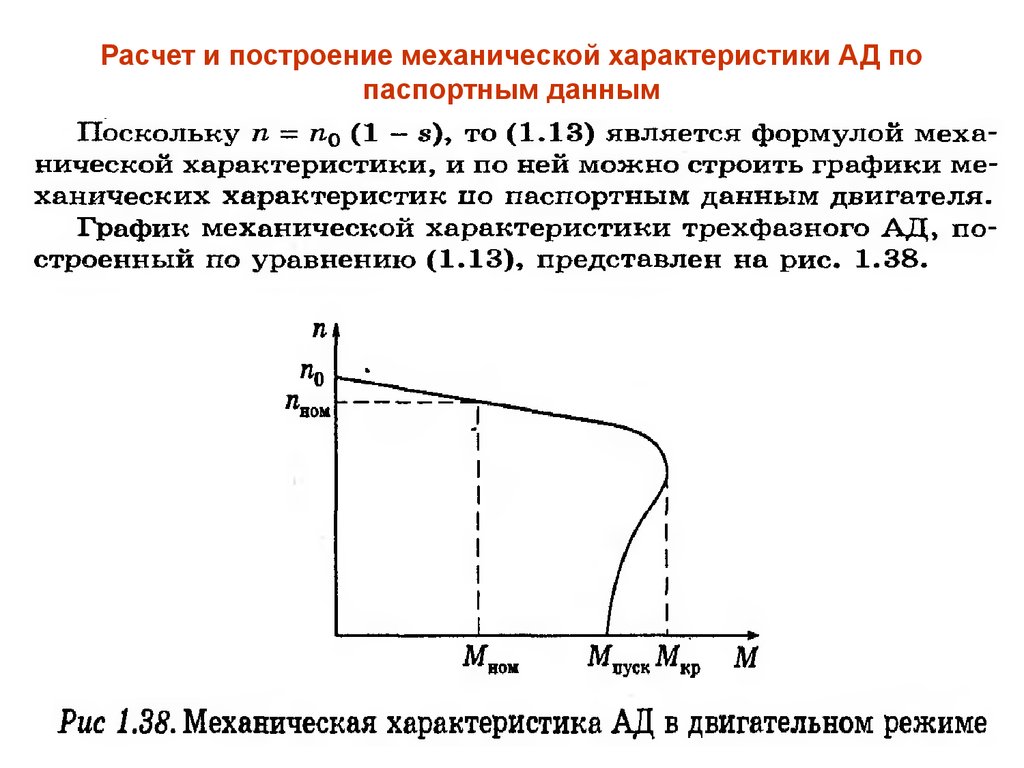
Поэтому характеристику 1 (рис. 263) можно получить путем суммирования характеристик 2 и 3, создаваемых этими клетками. Пусковой момент Мп такого двигателя значительно больше, чем момент М’п обычного короткозамкнутого двигателя. Механическая характеристика двигателя с глубокими пазами такая же, как и у двигателя с двойной беличьей клеткой.
Рис. 263. Механическая характеристика асинхронного двигателя с повышенным пусковым моментом (с двойной беличьей клеткой)
Рабочие характеристики.
Рабочими характеристиками асинхронного двигателя называются зависимости частоты вращения n (или скольжения s), момента на валу М2, тока статора I1 коэффициента полезного действия η и cosφ1, от полезной мощности Р2 = Рmx при номинальных значениях напряжения U1 и частоты f1 (рис. 264).
Рис. 264. Рабочие характеристики асинхронного двигателя
Они строятся только для зоны практической устойчивой работы двигателя, т.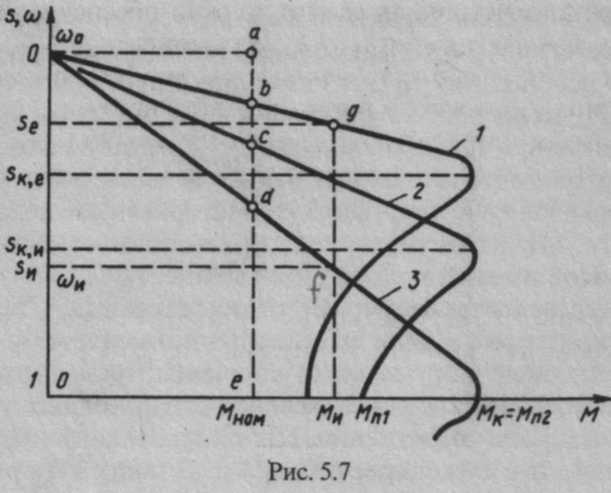 е. от скольжения, равного нулю, до скольжения, превышающего номинальное на 10—20%. Частота вращения n с ростом отдаваемой мощности Р2 изменяется мало, так же как и в механической характеристике; вращающий момент на валу М2 пропорционален мощности Р2, он меньше электромагнитного момента М на значение тормозящего момента Мтр, создаваемого силами трения.
е. от скольжения, равного нулю, до скольжения, превышающего номинальное на 10—20%. Частота вращения n с ростом отдаваемой мощности Р2 изменяется мало, так же как и в механической характеристике; вращающий момент на валу М2 пропорционален мощности Р2, он меньше электромагнитного момента М на значение тормозящего момента Мтр, создаваемого силами трения.
Ток статора I1, возрастает с увеличением отдаваемой мощности, но при Р2 = 0 имеется некоторый ток холостого хода I0. К. п. д. изменяется примерно так же, как и в трансформаторе, сохраняя достаточно большое значение в сравнительно широком диапазоне нагрузки.
Наибольшее значение к. п. д. для асинхронных двигателей средней и большой мощности составляет 0,75—0,95 (машины большой мощности имеют соответственно больший к. п. д.). Коэффициент мощности cosφ1 асинхронных двигателей средней и большой мощности при полной нагрузке равен 0,7—0,9.
Следовательно, они загружают электрические станции и сети значительными реактивными токами (от 70 до 40% номинального тока), что является существенным недостатком этих двигателей.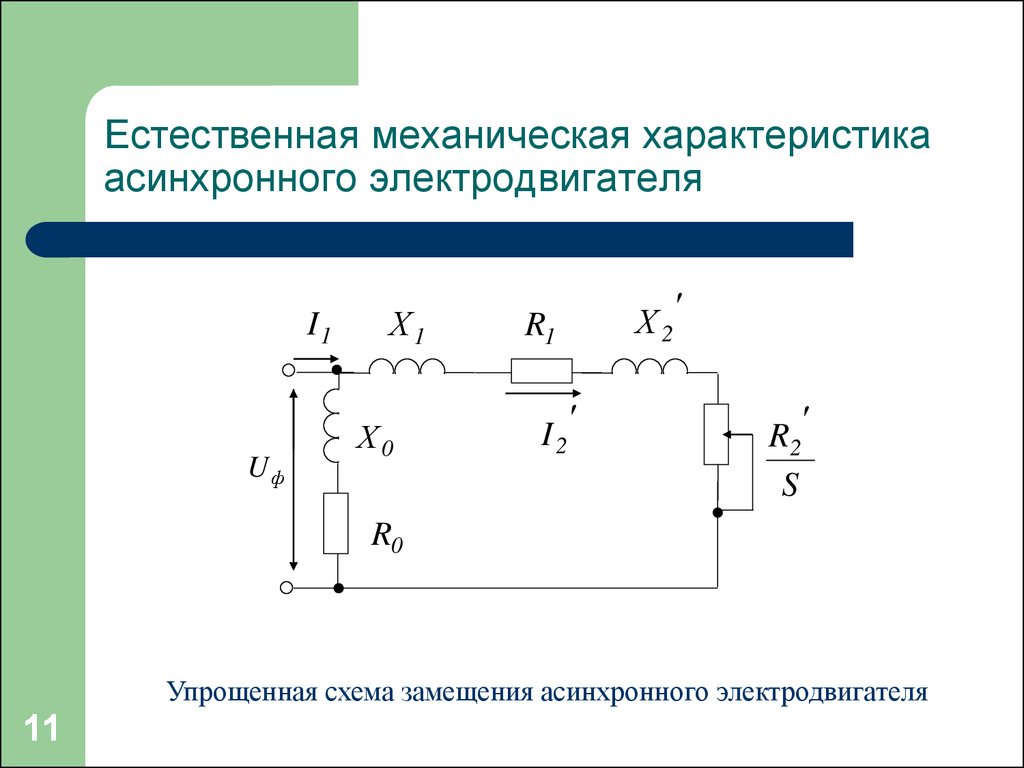
При нагрузках 25—50 % номинальной, которые часто встречаются при эксплуатации различных механизмов, коэффициент мощности уменьшается до неудовлетворительных с энергетической точки зрения значений (0,5—0,75).
При снятии нагрузки с двигателя коэффициент мощности уменьшается до значений 0,25—0,3, поэтому нельзя допускать работу асинхронных двигателей при холостом ходе и значительных недогрузках.
Работа при пониженном напряжении и обрыве одной из фаз.
Понижение напряжения сети не оказывает существенного влияния на частоту вращения ротора асинхронного двигателя. Однако в этом случае сильно уменьшается наибольший вращающий момент, который может развить асинхронный двигатель (при понижении напряжения на 30% он уменьшается примерно в 2 раза). Поэтому при значительном падении напряжения двигатель может остановиться, а при низком напряжении — не включиться в работу.
На э. п. с. переменного тока при уменьшении напряжения в контактной сети соответственно уменьшается и напряжение в трехфазной сети, от которой питаются асинхронные двигатели, приводящие во вращение вспомогательные машины (вентиляторы, компрессоры, насосы).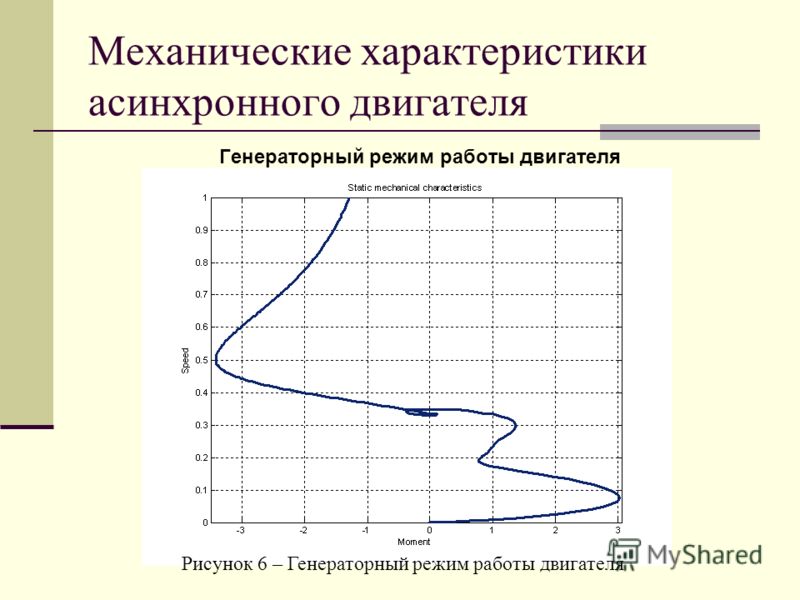
Для того чтобы обеспечить нормальную работу асинхронных двигателей при пониженном напряжении (они должны нормально работать при уменьшении напряжения до 0,75Uном), мощность всех двигателей вспомогательных машин на э. п. с. берется примерно в 1,5—1,6 раза большей, чем это необходимо для привода их при номинальном напряжении.
Такой запас по мощности необходим также из-за некоторой несимметрии фазных напряжений, так как на э. п. с. асинхронные двигатели питаются не от трехфазного генератора, а от расщепителя фаз.
При несимметрии напряжений фазные токи двигателя будут неодинаковы и сдвиг между ними по фазе не будет равен 120°. В результате по одной из фаз будет протекать больший ток, вызывающий увеличенный нагрев обмоток данной фазы. Это заставляет ограничивать нагрузку двигателя по сравнению с работой его при симметричном напряжении.
Кроме того, при несимметрии напряжений возникает не круговое, а эллиптическое вращающееся магнитное поле и несколько изменяется форма механической характеристики двигателя. При этом уменьшаются его наибольший и пусковой моменты.
При этом уменьшаются его наибольший и пусковой моменты.
Несимметрию напряжений характеризуют коэффициентом несимметрии, который равен среднему относительному (в процентах) отклонению напряжений в отдельных фазах от среднего (симметричного) напряжения. Систему трехфазных напряжений принято считать практически симметричной, если этот коэффициент меньше 5 %.
При обрыве одной из фаз двигатель продолжает работать, но по неповрежденным фазам будут протекать повышенные токи, вызывающие увеличенный нагрев обмоток; такой режим не должен допускаться. Пуск двигателя с оборванной фазой невозможен, так как при этом не создается вращающееся магнитное поле, вследствие чего ротор двигателя не будет вращаться.
Использование асинхронных двигателей для привода вспомогательных машин э. п. с. обеспечивает значительные преимущества по сравнению с двигателями постоянного тока. При уменьшении напряжения в контактной сети частота вращения асинхронных двигателей, а следовательно, и подача компрессоров, вентиляторов, насосов практически не изменяются.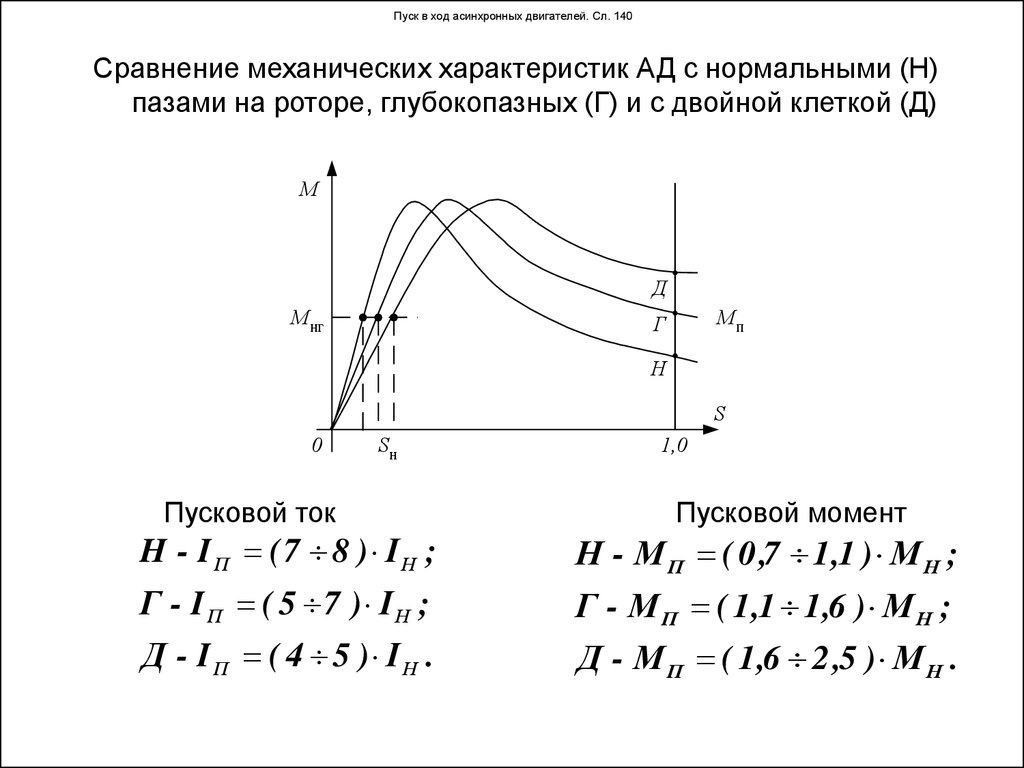 В двигателях же постоянного тока частота вращения пропорциональна питающему напряжению, поэтому подача этих машин существенно уменьшается.
В двигателях же постоянного тока частота вращения пропорциональна питающему напряжению, поэтому подача этих машин существенно уменьшается.
Механическая характеристика асинхронного двигателя
Асинхронный двигатель преобразовывает электрическую энергию в механическую. Механическая характеристика асинхронного двигателя, электромеханическая и другие содержат информацию, без которой невозможна его правильная эксплуатация.
Эта конструкция достаточно широко применяется в различных сферах человеческой жизнедеятельности. Без них немыслима работа станков, транспортеров, подъемно-транспортных машин. Двигатели, обладающие небольшой мощностью, широко используются в автоматике.
ОГЛАВЛЕНИЕ
- Устройство асинхронной машины
- Принцип работы асинхронной машины
- Механическая характеристика
- Электромеханическая характеристика
- Рабочие характеристики
Устройство асинхронной машины
Схематичное устройство асинхронной машины
Классическая асинхронная машина состоит из 2 основных частей: ротора (подвижной) и статора (неподвижной). Три отдельные фазы составляют обмотку статора. С1, С2 и С3 — обозначения начала фаз. С3, С4 и С5 — соответственно концы фаз. Все они подсоединены к клеммному разъему по схеме звезда или треугольник, что показано на рисунках а, б, в. Схему выбирают учитывая паспортные данные двигателя и сетевое напряжение.
Три отдельные фазы составляют обмотку статора. С1, С2 и С3 — обозначения начала фаз. С3, С4 и С5 — соответственно концы фаз. Все они подсоединены к клеммному разъему по схеме звезда или треугольник, что показано на рисунках а, б, в. Схему выбирают учитывая паспортные данные двигателя и сетевое напряжение.
Статор создает внутри электродвигателя магнитное поле, которое постоянно вращается.
Ротор различают короткозамкнутый и фазный.
В короткозамкнутом скорость вращения не регулируется. Конструкция с ним проще и дешевле. Однако пусковой момент у него слишком мал по сравнению с машинами, у которых фазный ротор. Здесь скорость вращения регулируется за счет возможности ввода дополнительного сопротивления.
Принцип работы асинхронной машины
Подавая напряжение на обмотку статора, по каждой фазе можно наблюдать изменяющиеся магнитные потоки, которые по отношению друг к другу смещены на 120 градусов. Общий результирующий поток получается вращающимся и создает ЭДС внутри проводников ротора.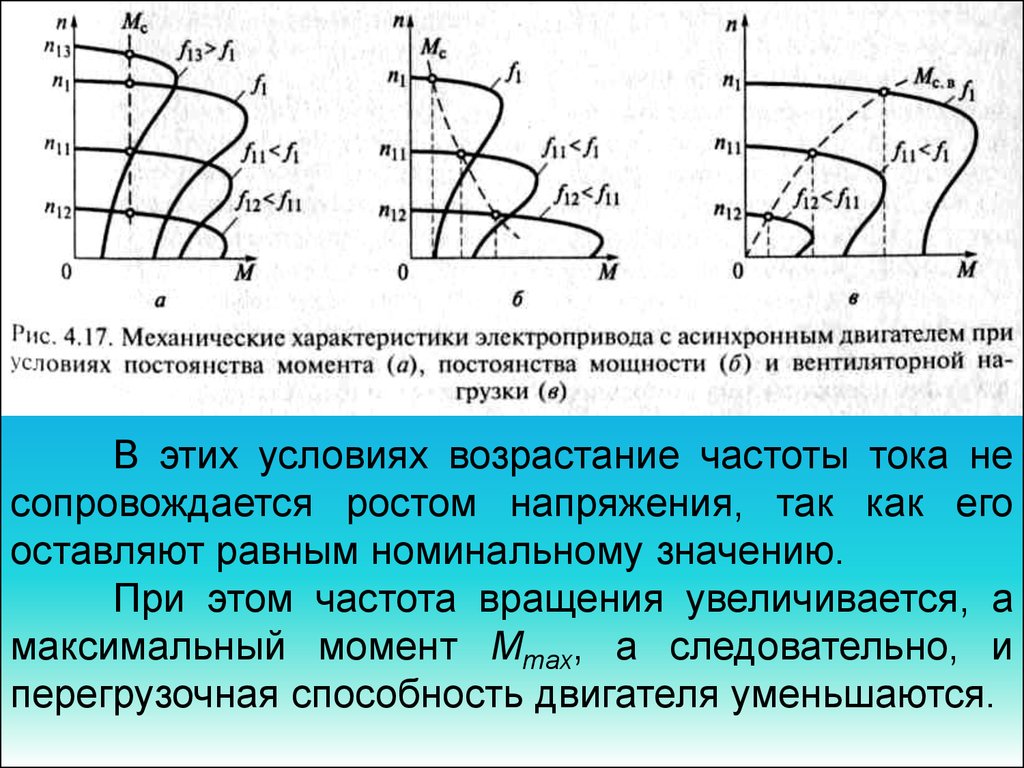
Там появляется ток, который во взаимодействии с результирующим потоком создает пусковой момент. Это приводит к вращению ротора.
Возникает скольжение S, т. е. разность между частотой вращения самого ротора n2 и частотой магнитного поля статора n1. Первоначально оно равно 1. Впоследствии частота возрастает, разность n1 – n2 уменьшается. Это ведет к уменьшению вращающего момента.
На холостом ходу скольжение минимально. Оно достигает критического значения Sкр, когда увеличивается статический момент. Превышение Sкр ведет к нестабильной работе машины.
Механическая характеристика
Как основная, помогает проводить детальный анализ работы электродвигателя. Она выражает непосредственную зависимость частоты вращения самого ротора от электромагнитного момента n=f (M).
Из графика видно, что на участке 1-3 машина работает устойчиво. 3-4 — непосредственный отрезок неустойчивой работы. Идеальный холостой ход соответствует точке 1.
Идеальный холостой ход соответствует точке 1.
Точка 2 — номинальный режим работы. Точка 3 — частота вращения достигла критического значения. Пусковой момент Мпуск — точка 4.
Наши читатели рекомендуют! Для экономии на платежах за электроэнергию наши читатели советуют ‘Экономитель энергии Electricity Saving Box’. Ежемесячные платежи станут на 30-50% меньше, чем были до использования экономителя. Он убирает реактивную составляющую из сети, в результате чего снижается нагрузка и, как следствие, ток потребления. Электроприборы потребляют меньше электроэнергии, снижаются затраты на ее оплату.
Существуют технические способы расчетов и построения механической характеристики с учетом данных паспорта.
В первоначальной точке 1 n0=60f/p (p – количество пар полюсов). Поскольку nн и Mн непосредственно координаты точки 2, расчет номинального момента производится по формуле Mн=9,55*Рн/ nн, где Рн — номинальная мощность. Значение nн указано в паспорте двигателя. В точке 3 Mкр=Mнλ. Пусковой момент в точке 4 Mпуск=Mн*λпуск (значения λ, λпуск — из паспорта).
Пусковой момент в точке 4 Mпуск=Mн*λпуск (значения λ, λпуск — из паспорта).
Механическая характеристика, построенная таким образом, называется естественной. Изменяя другие параметры можно получить искусственную механическую характеристику.
Полученные результаты дают возможность проанализировать и согласовать механические свойства самого двигателя и рабочего механизма.
Электромеханическая характеристика
Она являет собой зависимость угловой скорости вращения от тока статора. Используя несколько опорных точек можно построить электромеханическую характеристику. Номинальный ток рассчитывается по формуле:
Ток холостого хода составляет 30—40% от номинального.
Формула расчета при критическом скольжении:
Ток в начальный момент пуска:
Все значения отражают электромеханическую характеристику.
Рабочие характеристики
Рабочие характеристики асинхронного электродвигателя — это взаимосвязь нескольких параметров от полезной мощности P2. В их число входят: частота вращения самого ротора n2, момент на валу М, скольжение S, ток статора I1, расходуемая мощность P, коэффициент мощности СОSφ и КПД.
В их число входят: частота вращения самого ротора n2, момент на валу М, скольжение S, ток статора I1, расходуемая мощность P, коэффициент мощности СОSφ и КПД.
Причем частота электрического тока и напряжение неизменны, в отличие от нагрузки.
Как правило, рабочие характеристики асинхронного двигателя строятся в диапазоне значений скольжения от 0 до значения, превышающего номинальное на 10%. Это зона, где машина работает устойчиво.
Частота вращения ротора n2 уменьшается при возрастании нагрузки на валу. Но эти изменения не превышают 5%. Ток I1 растет, поскольку при последующем увеличении нагрузки его активная составляющая превышает реактивную.
СОSφ при холостом ходе мал. Но затем он возрастает. При повышенных нагрузках СОSφ уменьшается из-за возрастающего внутри обмотки ротора реактивного сопротивления.
КПД холостого хода равен 0. С увеличением нагрузки наблюдается его резкий рост, а впоследствии, снижение.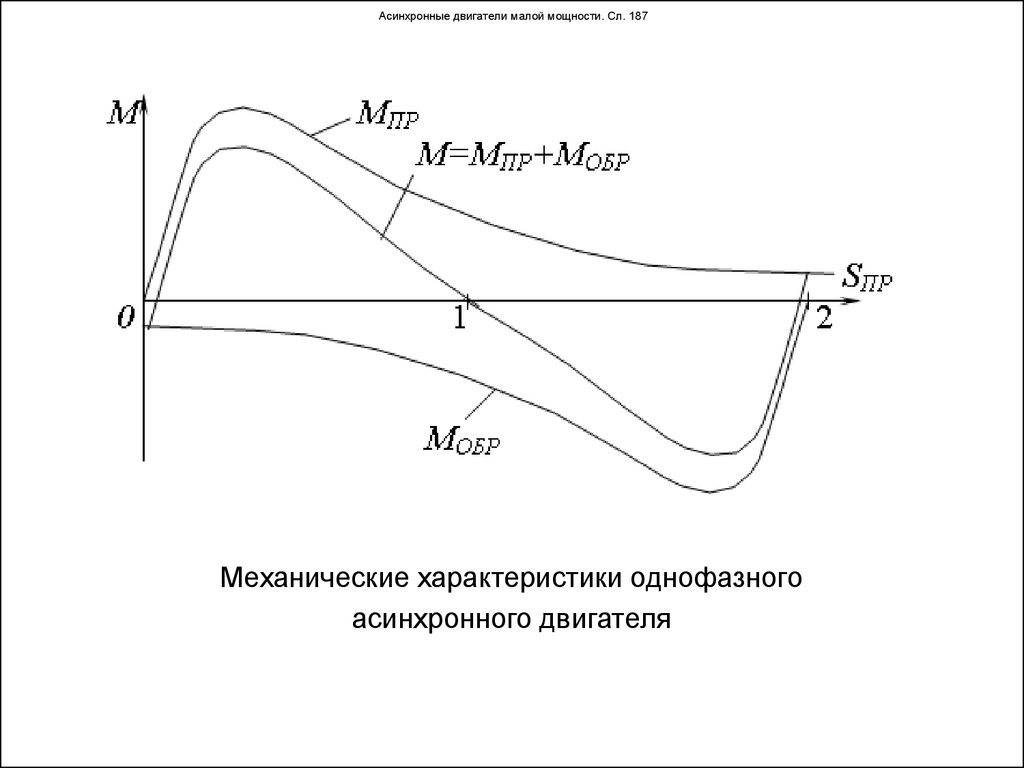
Механическая характеристика асинхронного двигателя
Механической характеристикой называется зависимость скорости асинхронного двигателя от момента на его валу.
Выражение механической характеристики можно получить из выражения потерь для асинхронного двигателя.
Δp2 = Pэм – P2 = M·ω0 – M·ω = M·(ω0 – ω) = M·ω0·s
Pэм – электромагнитная мощность – мощность, передаваемая через воздушный зазор из статора двигателя в ротор. Она может быть электрической и механической.
P2 – полезная мощность, может быть только механическая, и равна произведению момента на валу двигателя на его скорость.
ω0 – ω0·(1 – s) = ω0 – ω0 + ω0·s
Δp2 = 3·(I2’)2·r2’
3·(I2’)2·r2’ = M·ω0·s
Упрощенная формула механической характеристики асинхронного двигателя:
M = [3·(I2’)2·r2’] / [ω0·s] (1)
Подставим в формулу (1) значения тока I2’, определенного по схеме замещения.
Выражение полной формулы механической характеристики:
M = [3·Uф2·(r2’/s)] / [ω0·[(r1 + r2’/s)2 + xк2]] (2)
Если в формулу (2) подставить s от 0 до ±∞, то получится механическая характеристика асинхронного двигателя.
Механическая характеристика асинхронного двигателя.
Как видно из механической характеристики, она имеет два экстремума: первый в области положительных скольжений, второй в области отрицательных скольжений.
dM/ds = 0, можно определить максимальное значение момента, которое называют критическим моментом.
Mmax = Mкр = [3·Uф2] / [2·ω0·(r1 ± √(r12 + xк2))] (3)
sкр = ±(r2’/xк) (4)
Как видно из формулы (3), момент критический будет иметь разные значения, в области скольжений больше нуля будет знак «+», в области скольжений меньше нуля будет знак «–».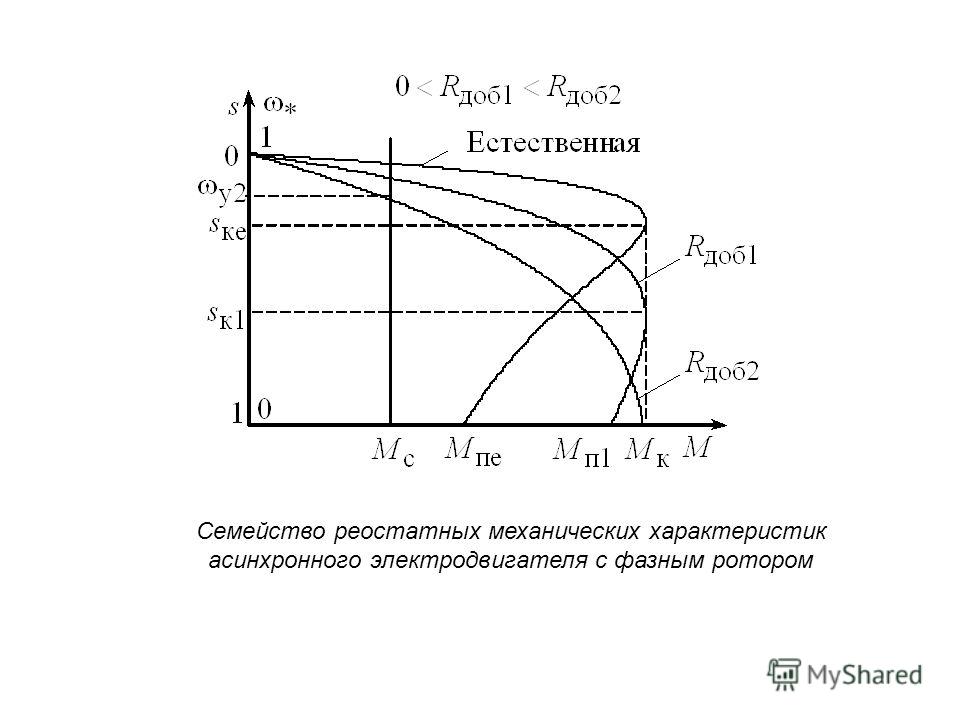
Величина критического скольжения одинаковая и в двигательном и в генераторном режимах, только имеет разные знаки.
Если выражение (1) разделить на выражение (2), можно получить, так называемую, формулу Клосса:
M = [2·Mк·(1 + a·sкр)] / [s/sкр + sкр/s + 2·a·sкр] (5)
a – это коэффициент.
a = r1/r2’
Обычно у асинхронных двигателей активное сопротивление статора r1 на порядок меньше активного сопротивления ротора r2’, поэтому с достаточной степенью точности можно записать, что r1=0, и тогда a=0.
M = [2·Mк] / [s/sкр + sкр/s] (6)
Если (5) называется полной формулой Клосса, то (6) называется упрощенной формулой Клосса.
Упрощенная формула критического момента:
Mкр = [3·Uф2] / [2·ω0·xкр]
В двигательном режиме скольжение изменяется от 1 до 0.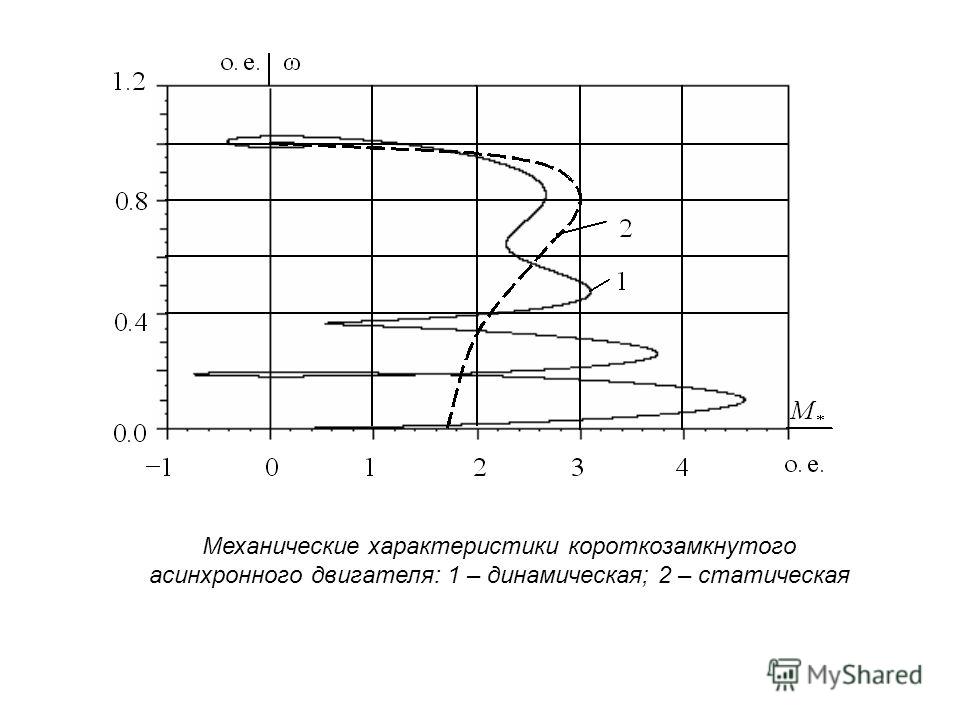
Рассмотрим анализ формулы Клосса для двигательного режима работы. Как видно из характеристики, ее можно разбить на два участка: s > sкр и s < sкр.
Рассмотрим участок s > sкр, тогда отношением sкр/s можно пренебречь:
M = 2·Mк· sкр / s = A/s
Как видно из получившейся формулы, связь между моментом и скольжением носит гиперболический характер. Это нелинейная не рабочая часть механической характеристики.
Рассмотрим участок s < sкр, тогда отношением s/sкр можно пренебречь:
M = 2·Mк·s / sкр = B·s
На участке s < sкр связь между моментом и скольжением линейная.
Из анализа формулы Клосса видно, что механическая характеристика имеет два участка: линейный рабочий и нелинейный нерабочий.
Для того чтобы определить характеристику двигателя в генераторном режиме, которая имеет также два участка: линейный и нелинейный, достаточно знать значение критического момента в генераторном режиме.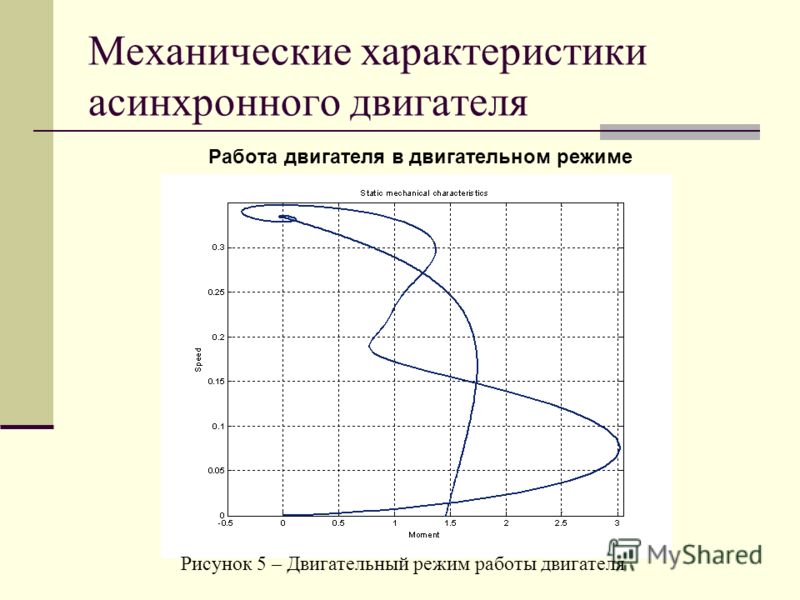 Нелинейная область в генераторном режиме не может быть использована из-за больших значений токов и моментов.
Нелинейная область в генераторном режиме не может быть использована из-за больших значений токов и моментов.
λ = Mкр.д./Mн
Критический момент можно определить для двигательного режима по паспортным данным, в них задается отношение Mкр.д./Mн.
Mкр.г. = Mкр.д. · [r1 + √(r12 + xк2)] / [r1 – √(r12 + xк2)]
- Схема включения и электромеханическая характеристика асинхронного двигателя
38. Механическая характеристика двигателя.
Механической характеристикой
двигателяназывается зависимость
частоты вращения ротора от момента на
валуn=f(M2). Так как при нагрузке
момент холостого хода мал, тоM2 ≈M и механическая
характеристика представляется
зависимостьюn=f(M). Если учесть взаимосвязьs= (n1 -n) /n1,
то механическую характеристику можно
получить, представив ее графическую
зависимость в координатахn и
М (рис.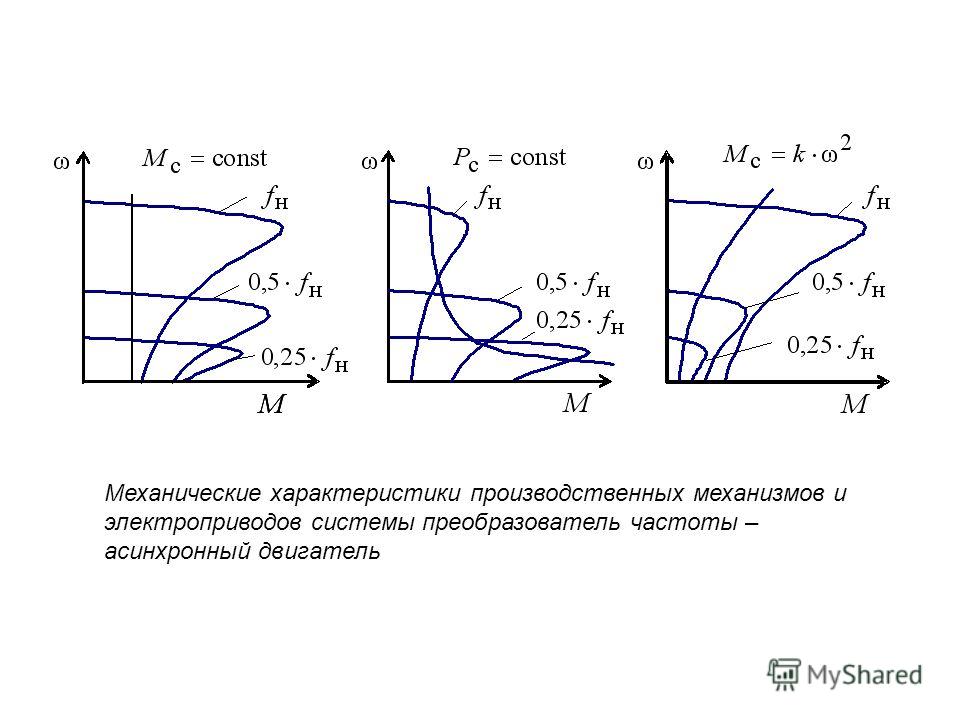 1).
1).
Рис. 1. Механическая характеристика
асинхронного двигателя
Естественная механическая характеристика
асинхронного двигателясоответствует
основной (паспортной) схеме его включения
и номинальным параметрам питающего
напряжения.Искусственные
характеристики получаются, если
включены какие-либо дополнительные
элементы: резисторы, реакторы, конденсаторы.
При питании двигателя не номинальным
напряжением характеристики также
отличаются от естественной механической
характеристики.
Механические характеристики являются
очень удобным и полезным инструментом
при анализе статических и динамических
режимов электропривода.
39.Основные точки механической характеристики: критическое скольжение и частота, максимальный момент, пусковой момент, номинальный момент.
Механическая
характеристика – это зависимость
вращающего момента от скольжения, или,
иначе говоря, от числа оборотов:
Из выражения
видно, что эта зависимость очень
сложна, поскольку, как показывают
формулы)и,
скольжение входит также в выражения
дляI2иcosϕ2.
Механическая характеристика асинхронного
двигателя дается обычно графически
Начальная точка
характеристики соответствует n=
0 иs= 1: это первое мгновение
пуска двигателя. Величина пускового
вращающего моментаMn–
очень важная характеристика эксплуатационных
свойств двигателя. ЕслиMnмал,
меньше номинального рабочего момента,
двигатель может запускаться только
вхолостую или при соответственно
сниженной механической нагрузке.
Обозначим
символом Mnpпротиводействующий
(тормозной) момент, создаваемый
механической нагрузкой на валу, при
которой двигатель пускается. Очевидным
условием для возможности запуска
двигателя является:Mn>Mnp.
Если это условие выполнено, ротор
двигателя придет в движение, число
оборотов егоnбудет возрастать,
а скольжениеsуменьшаться.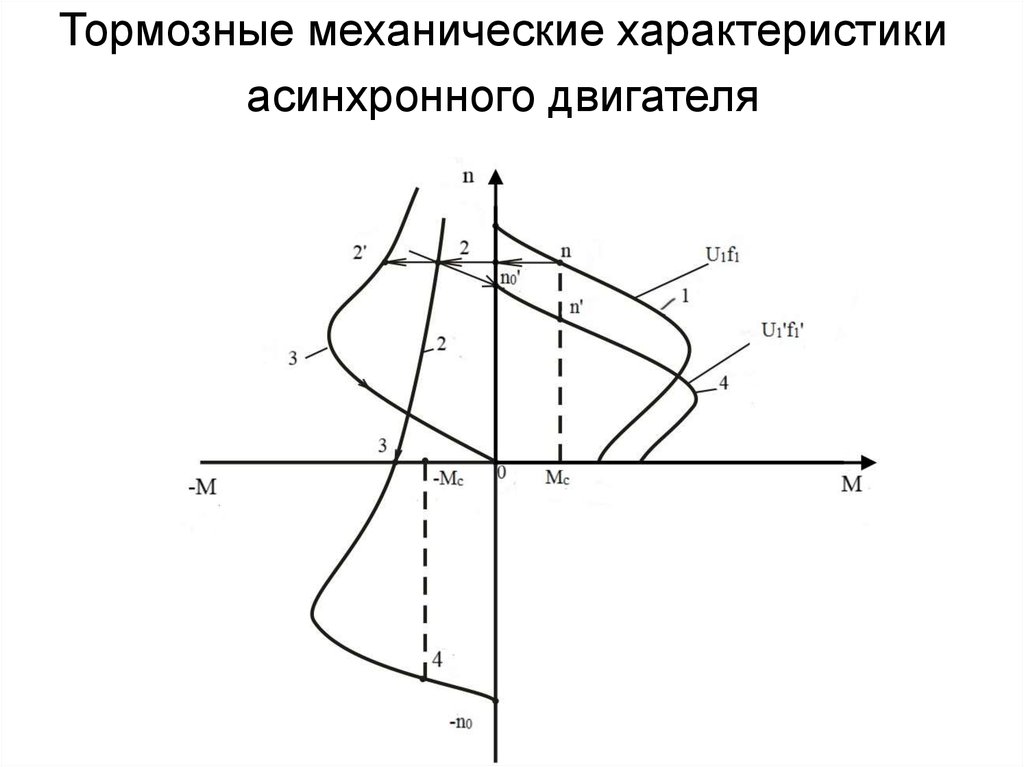
Как видно из изображения выше, вращающий
момент двигателя при этом растет отMnдо
максимальногоMm,
соответствующего критическому
скольжениюskp,
следовательно, растет и избыточная
располагаемая мощность двигателя,
определяемая разностью моментовMиMnp.
Чем больше разность
между располагаемым моментом двигателя
(возможным при данном скольжении по
рабочей характеристике) Ми
противодействующимМnp,
тем легче режим запуска и тем быстрее
двигатель достигает установившейся
скорости вращения.
Как показывает
механическая характеристика, при
некотором числе оборотов (при s=skp)
располагаемый вращающий момент двигателя
достигает максимально возможного для
данного двигателя (при данном напряженииU)
значенияMт.
Далее двигатель продолжает увеличивать
скорость вращения, но располагаемый
вращающий момент его быстро уменьшается.
При каких-то значенияхnиsвращающий
момент двигателя становится равным
противодействующему: пуск двигателя
заканчивается, число оборотов его
устанавливается на значении, соответствующем
соотношению:
Это соотношение
является обязательным для всех нагрузочных
режимов двигателя, то есть для всех
значений Mnp, не
выходящих за пределы максимального
располагаемого вращающего момента
двигателяМт.
В этих пределах двигатель сам автоматически
приспосабливается ко всем колебаниям
нагрузки: если во время работы двигателя
его механическая нагрузка увеличивается,
на какое-то мгновениеMnpстанет
больше момента, развиваемого двигателем.
Обороты двигателя начнут снижаться, а
момент увеличиваться.
Скорость вращения
установится на новом уровне, отвечающем
равенству MиMnp.
При снижении нагрузки процесс перехода
к новому нагрузочному режиму будет
обратным.
Если нагрузочный
момент MnpпревыситМт,
двигатель сразу остановится, так как с
дальнейшим уменьшением оборотов
вращающий момент двигателя уменьшается.
Поэтому максимальный
момент двигателя Мтназывается
еще опрокидывающим или критическим
моментом.
Если в формулу
момента подставить:
и
то получим:
Взяв первую
производную от Мпои
приравняв ее к нулю, найдем, что
максимальное значение вращающего
момента наступает при условии:
то есть при таком
скольжении s=skp,
при котором активное сопротивление
ротора равно индуктивному сопротивлению
Значения skpу
большинства асинхронных двигателей
лежат в пределах 10 – 25%.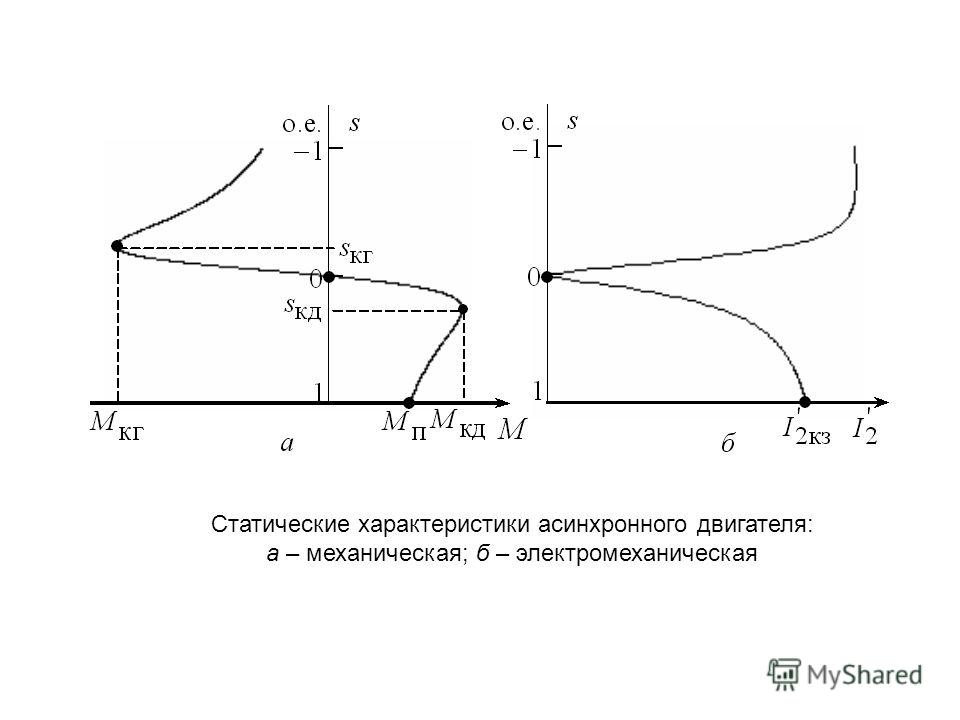
Если в написанную
выше формулу момента вместо активного
сопротивления r2подставить
индуктивное по формуле
получим:
Максимальный
вращающий момент асинхронного двигателя
пропорционален квадрату магнитного
потока (а значит, и квадрату напряжения)
и обратно пропорционален индуктивности
рассеяния обмотки ротора.
При постоянстве
напряжения, подводимого к двигателю,
его поток Фостается
практически неизменным.
Индуктивность
рассеяния роторной цепи тоже практически
постоянна. Поэтому при изменении
активного сопротивления в цепи ротора
максимальное значение вращающего
момента Mтизменяться
не будет, но будет наступать при разных
скольжениях (с увеличением активного
сопротивления ротора – при больших
значениях скольжения).
Очевидно, что
максимум возможной нагрузки двигателя
определяется значением его Mт.
Рабочая часть характеристики двигателя
лежит в узком диапазоне чисел оборотов
отn, соответствующегоMт,
до. Приn=n1(конечная
точка характеристики)М=
0, так как при синхронной скорости
ротораs= 0 иI2=
0.
Номинальный
вращающий момент, определяющий значение
паспортной мощности двигателя, принимается
обычно равным 0,4 – 0,6 от Mт.
Таким образом, асинхронные двигатели
допускают кратковременные перегрузки
в 2 – 2,5 раза.
Основным параметром,
характеризующим режим работы асинхронного
двигателя, является скольжение s –
относительная разность частоты вращения
ротора двигателя n и его поля nо:
s = (no —
n) / no.
Область механической
характеристики, соответствующая 0 ≤ s
≤ 1 – область двигательных режимов,
причем при s < sкр работа
двигателя устойчива, при s > sкр –
неустойчива.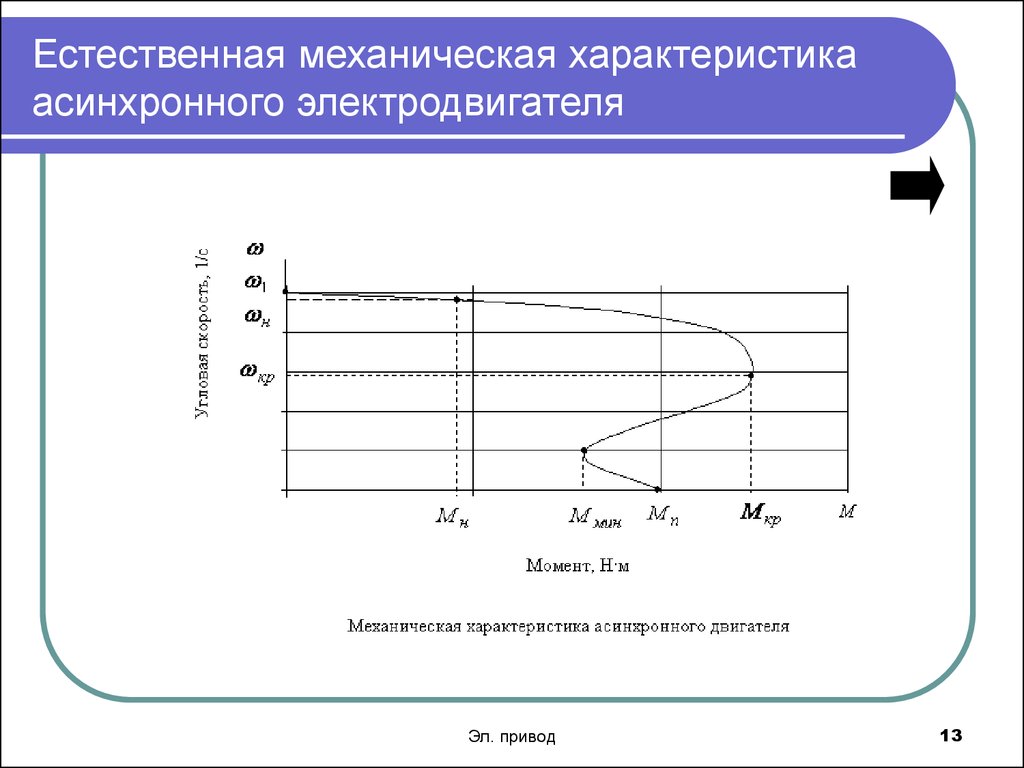 При s < 0 и s > 1 момент
При s < 0 и s > 1 момент
двигателя направлен против направления
вращения его ротора (соответственно
рекуперативное торможение и торможение
противовключением).
Устойчивый участок
механической характеристики двигателя
часто описывается формулой Клосса,
подстановкой в которую параметров
номинального режима можно определить
критическое скольжение sкр:
,
где: λ = Mkp /
Mн –
перегрузочная способность двигателя.
Механическая
характеристика по данным справочника
или каталога приближенно может быть
построена по четырем точкам (рис.7.1):
точка 1 – идеальный
холостой ход, n = no =
60 f / p, М = 0, где: р — число пар полюсов
магнитного поля двигателя;точка 2 — номинальный,
режим: n = nн,
М = Мн =
9550 Pн /
nн,
где Pн –
номинальная мощность двигателя в кВт;точка 3 – критический
режим: n = nкр,
М = Мкр =λ
Мн ;точка 4 – режим
пуска: n = 0, М = Мпуск =
β Мн.
При анализе работы
двигателя в диапазоне нагрузок до Мн и
несколько больше устойчивый участок
механической характеристики можно
приближенно описать уравнением прямой
линии n=n0-вМ,
где коэффициент “в” легко определяется
подстановкой в уравнение параметров
номинального режима nн и
Мн.
Механические характеристики асинхронных электродвигателей (лекция 4)
Похожие презентации:
Технология перевозочного процесса
3D печать и 3D принтер
Организация работы и расчет техникоэкономических показателей участка механической обработки детали
Грузоподъемные машины. (Лекция 4.1.2)
Видеокарта. Виды видеокарт
Безопасное проведение работ на высоте
Анализ компании Apple
Геофизические исследования скважин
Трансформаторы тока и напряжения
Транзисторы
1. Механические характеристики асинхронных электродвигателей
Курс1. Часть2. Регулирование
Часть2. Регулирование
частоты вращения
электроприводов постоянного и
переменного тока
Механические характеристики
асинхронных
электродвигателей
1.
2.
3.
1
Модель асинхронного электродвигателя.
Естественная механическая характеристика
асинхронного электродвигателя.
Управление пуском асинхронных
электродвигателей. Расчет пусковых реостатов
2. Модель асинхронного электродвигателя.
Достоинства асинхронного электродвигателя:
простота конструкции;
низкая металлоемкость;
допускает прямой пуск от сети;
повышенная надежность;
простота в ремонте и эксплуатации.
2
3. Модель асинхронного электродвигателя.
Асинхронного электродвигатели
изготавливают двух типов с фазным
и короткозамкнутым ротором.
0
3
4. Модель асинхронного электродвигателя.
Электродвигатели с короткозамкнутым ротором
имеют обмотку ротора в виде «беличьей клетки». Она
постоянна замкнута в лобовых частях ротора при
помощи короткозамкнутых колец.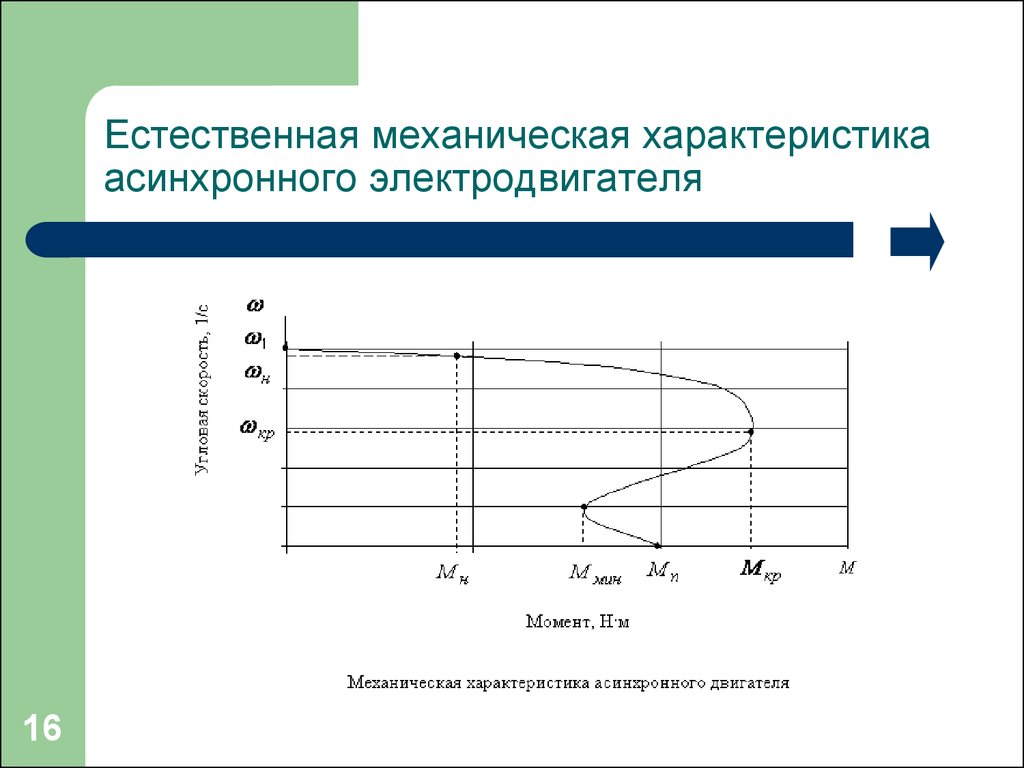 К ним подсоединены
К ним подсоединены
стержни проводники, которые размещены в пазах
сердечника ротора.
4
5. Модель асинхронного электродвигателя.
а)
б)
в)
5
г)
6. Модель асинхронного электродвигателя.
Пусть на статоре расположена катушка А-Х по
которой протекает переменный ток
iА = Im sin t; = 2 f1.
МДС FА, созданная этим током, будет пульсировать по
оси обмотки
FА = Fm sin t.
6
7. Модель асинхронного электродвигателя.
Если добавить катушку В-Y, расположенную под углом
900 и пропускать по ней ток
iВ = Im cos t, то
МДС FВ будет пульсировать по оси этой обмотки
FВ = Fm cos t.
7
8. Модель асинхронного электродвигателя.
Вектор результирующей МДС имеет модуль
F
2
FA
2
FB
Fm const .
Его фаза определится из условия
FA
tg
tg t
FB
Таким образом, вектор результирующей МДС
вращается с угловой скоростью
8
2 f 1 .
9. Модель асинхронного электродвигателя.

Частота вращения магнитного поля n1 как и
угловая скорость ω1 находится в строгой зависимости от
частоты подводимого напряжения сети f1 и числа пар
полюсов р двигателя:
60 f 1
п1
,
p
9
2 f 1
1
.
p
10. Модель асинхронного электродвигателя.
Наведение в обмотке ротора ЭДС и появление
вращающего или тормозящего момента асинхронного
Двигателя возможно только при наличии разности
Между угловыми скоростями вращения магнитного
поля статора и ротора. Это различие оценивают в
относительных единицах и называют скольжением
10
1 2
S
.
1
11. Естественная механическая характеристика асинхронного электродвигателя
I1
Uф
Х1
Х0
R1
I 2
Х 2
R2
S
R0
Упрощенная схема замещения асинхронного электродвигателя
11
12. Естественная механическая характеристика асинхронного электродвигателя
2
Uф
R2 2
( R1
) ( X 1 X 2 )2
S
Вращающий момент асинхронного двигателя может
быть определен из выражения потерь :
1 S 3( 2
12
3( 2 ) 2 R2
) R2
.
1 S
3U ф 2 R2
2
R2 2
2
1 ( R1
) ( X 1 X 2 ) S
S
13. Естественная механическая характеристика асинхронного электродвигателя
2
13
1
1
2
14. Естественная механическая характеристика асинхронного электродвигателя
R2/ R12 S 2 ( X 1 X 2/ )2 S 2
dM 3 U ф R2
0,
2
/
2
/
2
2
dS
1
( R1 S R2 ) ( X 1 X 2 ) S
2
/
R2/ R12 S 2 ( X 1 X 2/ )2 S 2 0 R2/ R12 S 2 ( X 1 X 2/ )2 S 2
sк
Mк
14
R2
R12 ( X 1 X 2 )2
3U 2
2 0 R1 R12 ( X 1 X 2 )2
15. Естественная механическая характеристика асинхронного электродвигателя
Разделив уравнение механической характеристики на
выражение для максимального момента получим
2М к ( 1 Sк )
R1
М
, /.
S Sк
R2
2 S к
Sк
S
Приняв
2 S к q ,
окончательно получаем
15
М дв
М кр ( 2 q )
S кр
S
q
S кр
S
.
16. Естественная механическая характеристика асинхронного электродвигателя
16
17.
 Естественная механическая характеристика асинхронного электродвигателя
Естественная механическая характеристика асинхронного электродвигателя
Характерными точками механической характеристики
являются:
• пусковая точка – М=Мп; ω=0;
• точка провала на пусковой ветви, угловая скорость,
• в которой соответствует скольжению S=0,8; М=Ммин;
• критическая точка с координатами ωк, Мк;
• номинальная точка – ωн, Мн;
• точка холостого хода – ω=ω1; М=0.
17
18. Управление пуском асинхронных электродвигателей. Расчет пусковых реостатов
Кратность начального пускового момента двигателя
составляет
Мп
kм
1…1,8
Мн
а кратность начального пускового тока
Iп
k I 5…7
Iн
Отсутствие пропорциональности между моментом
двигателя и током статора во время пуска объясняется
значительным снижением магнитного потока.
18
19. Управление пуском асинхронных электродвигателей. Расчет пусковых реостатов
Для повышения начального пускового момента и
снижения пускового тока применяются
короткозамкнутые двигатели специальных конструкций,
у которых ротор имеет две клетки, расположенные
концентрически, или глубокие пазы с высокими и
узкими стержнями.
19
20. Управление пуском асинхронных электродвигателей. Расчет пусковых реостатов
У двигателей с контактными кольцами начальный
пусковой момент увеличивается по мере возрастания
до известных пределов сопротивления реостата.
величина начального пускового момента может быть
доведена до величины критического момента.
пусковой ток при увеличении сопротивления
уменьшается.
20
21. Управление пуском асинхронных электродвигателей. Расчет пусковых реостатов
Mн
К расчету пускового реостата асинхронного двигателя
21
22. Управление пуском асинхронных электродвигателей. Расчет пусковых реостатов
Методика расчета:
•на характеристике Мдв=f( ), наносятся границы пуска;
•через точки d и d1 естественной механической
характеристики, соответствующие значениям моментов
Мпуск макс и Мпуск мин, проводится прямая до пересечения
с линией синхронной скорости (S=0) в точке t;
•из полученной точки проводится пусковая
характеристика до точки с координатами Мпуск макс, ω=0;
22
23.
 Управление пуском асинхронных электродвигателей. Расчет пусковых реостатов
Управление пуском асинхронных электродвигателей. Расчет пусковых реостатов
•в точке с координатами Мпуск мин, ω=ω3 происходит
отключение первой ступени реостата;
•в точке с координатами Мпуск мин, ω=ω2 происходит
отключение второй ступени реостата;
•отрезок [ed] пропорционален величине активного
сопротивления одной фазы ротора. Соответственно
отрезок [dc] в относительных единицах пропорционален
сопротивлению первой ступени пускового реостата,
отрезок [bс] – второй ступени.
23
24. Управление пуском асинхронных электродвигателей. Расчет пусковых реостатов
Измерив длины этих отрезков, определяют величины
сопротивления каждой ступени пускового реостата:
R1
где
24
dc R
ed рот
R рот
U 2 н Sн
3I 2 н
.
R2
или
cb R
ed рот
R рот
Рн S н
3 2н н
2
.
25. Управление пуском асинхронных электродвигателей. Расчет пусковых реостатов
При реостатном пуске асинхронного электродвигателя
с контактными кольцами поочередное закорачивание
ступеней пускового сопротивления может
производиться автоматически при помощи контакторов,
управление включением которых может осуществляться
в функции времени, частоты вращения, тока или
частоты тока ротора.
25
26. Управление пуском асинхронного электродвигателя. Расчет пусковых реостатов
Для обеспечения заданной диаграммы пуска необходима
фиксация моментов подачи команд на включение
контакторов. Это может осуществляться следующими
способами:
•путем отсчета промежутков времени Δt1, Δt2, Δt3,
для чего используются реле времени;
• посредством контроля значения скорости двигателя
или ЭДС ротора, что может быть сделано при помощи
датчиков скорости или ЭДС;
•применением датчиков тока;
•посредством контроля частоты тока ротора .
26
27. Управление пуском асинхронного электродвигателя. Расчет пусковых реостатов
SB1
KM1
KM1
SB2
KM1
KT1
M2
KM4
M1
KM4
KM4
KT1:1
KT1:2
KM2
KM3
R31…R33
KM3
R21…R23
27
KM2
R11…R13
KT1:3
KM4
Схема электрическая принципиальная управления
пуском асинхронного двигателя в функции времени
28. Управление пуском асинхронного электродвигателя.
 Расчет пусковых реостатов
Расчет пусковых реостатов
Время пребывания на каждой ступени пускового
реостата определяется по следующему соотношению:
ti
о S нi
Мн
ln
М дин 1i
М дин 2i
,
Мдин 1i=Мпуск макс–Мсi; M дин 2i=Мпуск мин–Мсi.
28
English
Русский
Правила
Расчет механической характеристики асинхронного электродвигателя для работы в составе приводов буровых установок
Автор:
Филин Виталий Андреевич
Рубрика: Технические науки
Опубликовано
в
Молодой учёный
№38 (328) сентябрь 2020 г.
Дата публикации: 15.09.2020
2020-09-15
Статья просмотрена:
164 раза
Скачать электронную версию
Скачать Часть 1 (pdf)
Библиографическое описание:
Филин, В. А. Расчет механической характеристики асинхронного электродвигателя для работы в составе приводов буровых установок / В. А. Филин. — Текст : непосредственный // Молодой ученый. — 2020. — № 38 (328). — С. 15-19. — URL: https://moluch.ru/archive/328/73610/ (дата обращения: 13.09.2022).
А. Расчет механической характеристики асинхронного электродвигателя для работы в составе приводов буровых установок / В. А. Филин. — Текст : непосредственный // Молодой ученый. — 2020. — № 38 (328). — С. 15-19. — URL: https://moluch.ru/archive/328/73610/ (дата обращения: 13.09.2022).
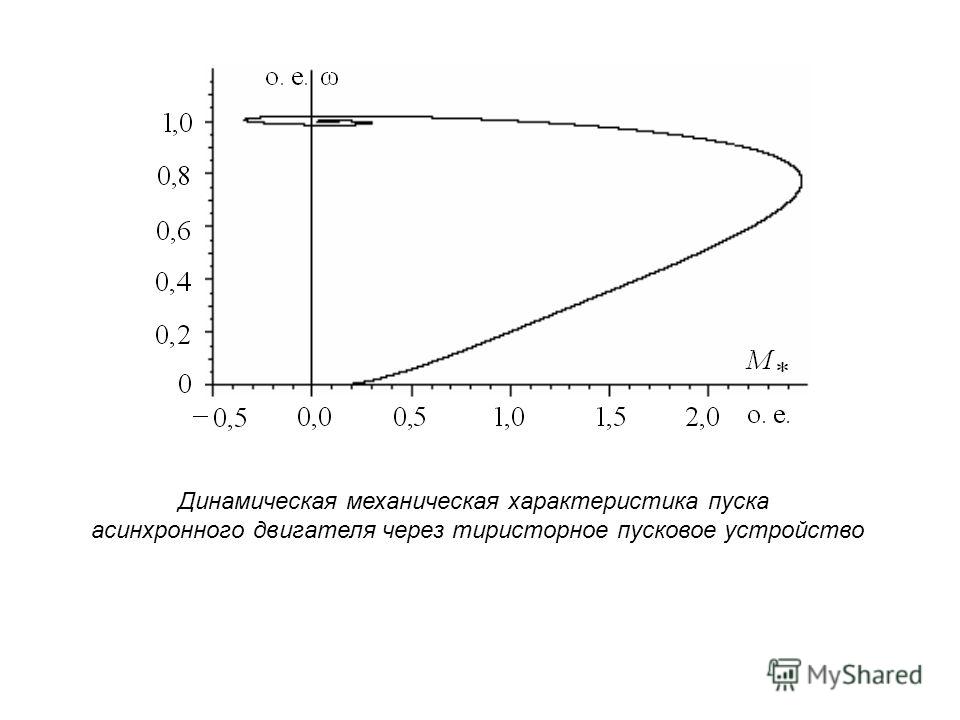
В статье представлен расчет механической характеристики асинхронного электродвигателя в составе буровой установки. Целью работы является построение механической характеристики асинхронного электродвигателя с помощью программы. В ходе работы выполняется построение зависимостей частоты вращения от момента, зависимостей момента от скольжения на основе аналитического метода и математического моделирования.
Ключевые слова:
асинхронный двигатель, механическая характеристика, электрический привод.
Ярко выраженной тенденцией производства электроприводов буровой установки является все более широкое применение асинхронных двигателей (АД). [6] Во многом это связанно с конструктивными особенностями АД, а именно простая конструкция, низкая стоимость из-за небольшого количества цветного металла, неприхотливые эксплуатационные условия. Основным соображением для проектировщика асинхронного двигателя является конструкция двигателя с высоким пусковым моментом, лучшим КПД и коэффициентом мощности.
[6] Во многом это связанно с конструктивными особенностями АД, а именно простая конструкция, низкая стоимость из-за небольшого количества цветного металла, неприхотливые эксплуатационные условия. Основным соображением для проектировщика асинхронного двигателя является конструкция двигателя с высоким пусковым моментом, лучшим КПД и коэффициентом мощности.
Но требования к энергоэффективности из года в год ужесточаются, что заставляет производителей идти на вынужденную модернизацию имеющихся моделей либо проектировать абсолютно новые. Для правильной эксплуатации двигателя силового привода важно знать, как будут меняться его основные параметры, т. е. крутящий момент М, частота вращения n и мощность N, в зависимости от нагрузки и изменения напряжения и частоты тока в питающейся сети.
Расчет механической характеристики возможно произвести тремя способами: аналитический методом, на основе формул и зависимостей, построение математической модели, экспериментальное исследование.
Таблица 1
Основные параметры АД при частоте сети 50 Гц
| |
Полезная мощности, кВт | 1200 |
Частота вращения (синхронная), об/мин | 500 |
Частота вращения, об/мин | 480 |
Отношение макс. момента к номинальному, о.е. | 1,8 |
Моменты, создаваемые двигателем и исполнительным органом рабочей машины, могут иметь разные значения при различных частотах вращения. При выборе электродвигателя необходимо, чтобы его электромеханические свойства соответствовали технологическим требованиям приводимой им рабочей машины. К электромеханическим свойствам в первую очередь относится механическая характеристика. Механической характеристикой электродвигателя называют зависимость между частотой вращения вала двигателя и развиваемым им
К электромеханическим свойствам в первую очередь относится механическая характеристика. Механической характеристикой электродвигателя называют зависимость между частотой вращения вала двигателя и развиваемым им
n = f(М)
. Вместо частоты вращения вала
n
можно записать
ω = f(М)
, так как эти величины пропорциональны
ω = πn/30
. [1] Под скольжением подразумевается величина в относительных единицах, которая характеризует отставание скорости вращения ротора от синхронной скорости вращения поля статора, создаваемого трехфазной обмоткой [2]
Скольжением асинхронной машины выражается отношением:
(1)
Электромагнитный момент М на валу асинхронной машины пропорционален величине магнитного потока и активной составляющей тока в обмотке ротора, которая зависит от величины скольжения.
(2)
где
m
— число фаз обмотки статора;
U
— фазное напряжение сети;
R
c
-активное сопротивление фазы обмотки статора;
R
p
— активное сопротивление фазы обмотки ротора, приведённое к статору;
Х
с
— индуктивное сопротивление фазы обмотки статора;
Х
р
— индуктивное сопротивление фазы обмотки ротора, приведённое к статору.
Критическое скольжение по параметрам обмоток двигателя определяется по формуле
(3)
Подставив (2) и (3) получим выражение для определения критического момента
(4)
Номинальный момент АД (Н∙м) вычисляется по формуле
(5)
где
P
ном
— номинальная мощность двигателя,
n
ном
— номинальная частота вращения.
Для расчета механической характеристики АД мощностью более 100 кВт пользуются упрощенной формулой Клосса.
(6)
Значение пускового момента АД можно определить постановкой
s = 1
в формулу (2) или по данным каталога, используя формулу
M
п
= K
м
M
ном
, где
K
м
— кратность пускового момента по отношению к номинальному.
Уравнения (6) в достаточной мере описывает механические свойства АД. В асинхронных электродвигателях с короткозамкнутым ротором в той или иной мере наблюдается явление вытеснения тока в стержнях ротора, в связи с чем их параметры непостоянны и механические характеристики значительно отличаются от характеристик, рассчитанных по формулам Клосса. В частности, у некоторых электродвигателей с КЗ ротором при малых скоростях вращения наблюдается снижение момента, вызванное влиянием высших гармоник поля. [3]
В частности, у некоторых электродвигателей с КЗ ротором при малых скоростях вращения наблюдается снижение момента, вызванное влиянием высших гармоник поля. [3]
Таблица 2
Численные расчетные значения вращающегося момента
| 0,04 | 0,065 | 0,131 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
| 23,87 | 34,38 | 42,97 | 39,49 | 31,66 | 25,55 | 21,19 | 18,01 | 15,01 | 13,79 | 12,32 | 11,14 |
| 480 | 467 | 434 | 400 | 350 | 300 | 250 | 200 | 150 | 100 | 50 | 0 |
Выдвигаем гипотезу, что при математическом моделировании будет более высокая точность расчета механической характеристики.
Для достижения поставленных задач воспользуемся пакетом прикладных программ Elcut Студенческая версия. Elcut — это программное обеспечение для моделирования мультифизических задач. К его преимуществам относятся довольно простой процесс моделирования, дружественный интерфейс и незначительное потребление ресурсов. Также стоит отметить: это ПО является продуктом отечественной компании, что благоприятно сказывается на его доступности в условиях сложной политической обстановки. [5]
Расчет машины проводился методом конечных элементов. В основе электромагнитного расчета лежит модель, включающая в себя геометрию машины, магнитные и электрические свойства её активных материалов, режимные параметры и действующие нагрузки. В ходе расчёта определяются индукции и токи в сечениях модели. Затем определяются силы и моменты, а также энергетические показатели. [4]
Таблица 3
Численные моделируемые значения вращающегося момента
| 0,048 | 0,079 | 0,158 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
| 24,59 | 35,41 | 44,26 | 37,52 | 26,59 | 21,46 | 17,80 | 15,13 | 13,13 | 11,58 | 10,35 | 9,35 |
| 480 | 460 | 420 | 400 | 350 | 300 | 250 | 200 | 150 | 100 | 50 | 0 |
Рис. 1. Механическая характеристика асинхронного двигателя
1. Механическая характеристика асинхронного двигателя
В результате моделирования получен график зависимости медной обмотки статора и ротора (рис 2.). Программа выполняет расчет сил и моментов. Полученные значения переносим в MS Excel, так как функционал программы не позволяет работать с графиками. Итоговый вариант представлен на рис. 1. Электромагнитное поле создается током, протекающим в трехфазной обмотке статора. При изменении фазы тока наблюдается изменение плотности тока в обмотке ротора. На основании изменения фазы тока в обмотке статора, меняется плотность тока. В связи с выше сказанным, можно сделать вывод о правильности построения модели.
В ходе построения механических характеристик двумя способами совпадают до значения номинального момента. Последующим наиболее значимым отклонением является пусковой и критический момент.
Пусковой момент полученный при моделировании составляет
М
мод
= 9,35 кН∙м
что меньше расчетного пускового момента
М
расч
= 11,14 кН∙м
. Критическое скольжение отличается
Критическое скольжение отличается
s
к.рас
= 0,131
,
s
к.мод
= 0,159
. Предполагаю, что из-за эффекта вытеснения тока, связанного с влиянием высших гармоник поля.
Рис. 2. Построение механической характеристики в Elcut
В статье представлено построение механической характеристики асинхронного электродвигателя двумя методами: аналитический и математическое моделирование. Примером был выбран АД используемый в приводе трансмиссионного вала буровой установки.
В ходе расчетов были выявлены следующие последовательности: разница номинального момента между аналитическим и моделированным показателем составляет 3 %, критический момент — 2,9 %. В свою очередь пусковой момент — 16 %. Малое значение пускового момента оказывает влияние на величину критического момента.
На основании этого можно сделать вывод, что механическая характеристика АД, полученная в процессе моделирования, соответствует теории и является более корректной, чем характеристика, построенная аналитическим методом.
Литература:
- Ершов М. С., Яризов А. Д. Энергосберегающий электропривод технологических установок трубопроводного транспорта газа, нефти и нефтепродуктов: Учеб. пособие для вузов. М.: РГУ нефти и газа имени И. М. Губкина, 2011. -246 с.: ил.
- Вольдек А. И., Попов В. В. Электрические машины. Машины переменного тока. М.: Питер, 2008. 349 с. ISBN 978–5–469–01381–5.
- Лысенко О. А., Симаков А. В., Кузнецова М. А., Никонов А. В. Расчет механической характеристики асинхронного погружного электродвигателя методом конечных элементов // Омский научный вестник. 2018. № 6 (162). С. 55–60. DOI:10.25206/1813–8225–2018–162–55–60.
- Анненков А. Н., Филонов С. А., Шиянов А. И. Моделирование и поиск рациональной конструкции асинхронного двигателя малой мощности с повышенным пусковым моментом // Вестник ВГТУ. 2009. № 11.
- ELCUT 6.2. Руководство пользователя. СПб.: TOP, 2017. 287 с.
- IEA (2020), World Energy Balances: Overview, IEA, Paris https://www.
 iea.org/reports/world-energy-balances-overview
iea.org/reports/world-energy-balances-overview
Основные термины (генерируются автоматически): механическая характеристика, пусковой момент, критический момент, асинхронный двигатель, асинхронный электродвигатель, буровая установка, математическое моделирование, номинальный момент, частота вращения, аналитический метод.
Ключевые слова
асинхронный двигатель,
механическая характеристика,
электрический привод
асинхронный двигатель, механическая характеристика, электрический привод
Похожие статьи
Исследование
методов расчета параметров схемы замещения…
Математическая модель асинхронного двигателя во. .. Рассмотрим трехфазный асинхронный короткозамкнутый двигатель со следующими номинальными данными и параметрами схемы замещения [4]. Суммарный момент инерции двигателя и механизма, приведенный к валу…
.. Рассмотрим трехфазный асинхронный короткозамкнутый двигатель со следующими номинальными данными и параметрами схемы замещения [4]. Суммарный момент инерции двигателя и механизма, приведенный к валу…
Похожие статьи
Исследование
методов расчета параметров схемы замещения…
Математическая модель асинхронного двигателя во… Рассмотрим трехфазный асинхронный короткозамкнутый двигатель со следующими номинальными данными и параметрами схемы замещения [4]. Суммарный момент инерции двигателя и механизма, приведенный к валу…
ХАРАКТЕРИСТИКИ ДВИГАТЕЛЯ – Прикладное промышленное электричество
После введения компанией Edison в США системы распределения электроэнергии постоянного тока начался постепенный переход к более экономичной системе переменного тока. Освещение работало как на переменном токе, так и на постоянном. Передача электроэнергии на большие расстояния с меньшими потерями на переменном токе. Однако у двигателей была проблема с переменным током. Первоначально двигатели переменного тока были сконструированы как двигатели постоянного тока, но возникали многочисленные проблемы из-за изменяющихся магнитных полей.
Освещение работало как на переменном токе, так и на постоянном. Передача электроэнергии на большие расстояния с меньшими потерями на переменном токе. Однако у двигателей была проблема с переменным током. Первоначально двигатели переменного тока были сконструированы как двигатели постоянного тока, но возникали многочисленные проблемы из-за изменяющихся магнитных полей.
Рисунок 5.1. Схема семейства электродвигателей переменного тока. Никола Тесла представил себе совершенно новый тип двигателя, когда представил себе вращающуюся турбину, вращаемую не водой или паром, а вращающимся магнитным полем. Его новый тип двигателя, асинхронный двигатель переменного тока, по сей день является рабочей лошадкой в отрасли. Его прочность и простота обеспечивают долгий срок службы, высокую надежность и низкие эксплуатационные расходы. Тем не менее, небольшие коллекторные двигатели переменного тока, подобные двигателям постоянного тока, сохраняются в небольших бытовых приборах вместе с небольшими асинхронными двигателями Тесла. Мощность выше одной лошадиной силы (750 Вт) безраздельно властвует двигатель Tesla.
Мощность выше одной лошадиной силы (750 Вт) безраздельно властвует двигатель Tesla.
Современные твердотельные электронные схемы управляют бесколлекторными двигателями постоянного тока с помощью сигналов переменного тока, генерируемых источником постоянного тока. Бесщеточный двигатель постоянного тока, фактически двигатель переменного тока, заменяет обычный щеточный двигатель постоянного тока во многих приложениях. Шаговый двигатель , цифровая версия двигателя, приводится в действие прямоугольными волнами переменного тока, опять же, генерируемыми полупроводниковой схемой. На рисунке выше показано генеалогическое древо двигателей переменного тока, описанных в этой главе.
Круизные лайнеры и другие крупные суда заменяют приводные валы с редуктором на большие генераторы и двигатели мощностью в несколько мегаватт. Так было с дизель-электрическими локомотивами меньшего масштаба в течение многих лет.
Рисунок 5.2 Диаграмма уровня системы двигателя
На системном уровне (рисунок выше) двигатель получает электрическую энергию в виде разности потенциалов и протекающего тока, преобразуя ее в механическую работу. К сожалению, электродвигатели не на 100% эффективны. Часть электрической энергии теряется в виде тепла, другого вида энергии, из-за потерь I2R (также называемых потерями в меди) в обмотках двигателя. Тепло является нежелательным побочным продуктом этого преобразования. Он должен быть удален с двигателя и может отрицательно сказаться на долговечности. Таким образом, одной из целей является максимальное повышение КПД двигателя за счет снижения тепловых потерь. У двигателей переменного тока также есть некоторые потери, отсутствующие у двигателей постоянного тока: гистерезис и вихревые токи.
К сожалению, электродвигатели не на 100% эффективны. Часть электрической энергии теряется в виде тепла, другого вида энергии, из-за потерь I2R (также называемых потерями в меди) в обмотках двигателя. Тепло является нежелательным побочным продуктом этого преобразования. Он должен быть удален с двигателя и может отрицательно сказаться на долговечности. Таким образом, одной из целей является максимальное повышение КПД двигателя за счет снижения тепловых потерь. У двигателей переменного тока также есть некоторые потери, отсутствующие у двигателей постоянного тока: гистерезис и вихревые токи.
Большинство двигателей переменного тока являются асинхронными. Асинхронные двигатели предпочтительнее из-за их прочности и простоты. Фактически, 90% промышленных двигателей являются асинхронными.
Никола Тесла разработал основные принципы многофазного асинхронного двигателя в 1883 году и к 1888 году имел модель мощностью в половину лошадиной силы (400 Вт). Тесла продал права на производство Джорджу Вестингаузу за 65 000 долларов. Самые большие (> 1 л.с. или 1 кВт) промышленные двигатели являются многофазными асинхронными двигателями . Под многофазностью мы подразумеваем, что статор содержит несколько отдельных обмоток на полюс двигателя, приводимых в действие соответствующими сдвинутыми во времени синусоидами. На практике это две-три фазы. Большие промышленные двигатели трехфазные. Хотя для простоты мы включили многочисленные иллюстрации двухфазных двигателей, мы должны подчеркнуть, что почти все многофазные двигатели являются трехфазными. К 9 0009 асинхронный двигатель , мы имеем в виду, что обмотки статора индуцируют протекание тока в проводниках ротора, подобно трансформатору, в отличие от щеточного коллекторного двигателя постоянного тока.
Самые большие (> 1 л.с. или 1 кВт) промышленные двигатели являются многофазными асинхронными двигателями . Под многофазностью мы подразумеваем, что статор содержит несколько отдельных обмоток на полюс двигателя, приводимых в действие соответствующими сдвинутыми во времени синусоидами. На практике это две-три фазы. Большие промышленные двигатели трехфазные. Хотя для простоты мы включили многочисленные иллюстрации двухфазных двигателей, мы должны подчеркнуть, что почти все многофазные двигатели являются трехфазными. К 9 0009 асинхронный двигатель , мы имеем в виду, что обмотки статора индуцируют протекание тока в проводниках ротора, подобно трансформатору, в отличие от щеточного коллекторного двигателя постоянного тока.
Конструкция асинхронного двигателя переменного тока
Асинхронный двигатель состоит из ротора, известного как якорь, и статора с обмотками, подключенными к многофазному источнику энергии, как показано на рисунке ниже. Простой двухфазный асинхронный двигатель, показанный ниже, аналогичен двигателю мощностью 1/2 лошадиной силы, который Никола Тесла представил в 1888 году. 0003 Рисунок 5.3 Многофазный асинхронный двигатель Тесла
0003 Рисунок 5.3 Многофазный асинхронный двигатель Тесла
Статор на рисунке выше намотан парами катушек, соответствующих фазам доступной электрической энергии. Статор двухфазного асинхронного двигателя имеет 2 пары катушек, по одной паре для каждой из двух фаз переменного тока. Отдельные катушки пары соединены последовательно и соответствуют противоположным полюсам электромагнита. То есть одна катушка соответствует N-полюсу, другая — S-полюсу до тех пор, пока фаза переменного тока не изменит полярность. Другая пара катушек ориентирована 90° в пространстве к первой паре. Эта пара катушек подключена к переменному току, сдвинутому во времени на 90° в случае двухфазного двигателя. Во времена Теслы источником двух фаз переменного тока был двухфазный генератор переменного тока. Статор на рисунке выше имеет выступающих , явно выступающих полюсов, которые использовались в раннем асинхронном двигателе Теслы. Эта конструкция по сей день используется для двигателей малой мощности (<50 Вт). Однако для более крупных двигателей меньшая пульсация крутящего момента и более высокий КПД получаются, если катушки встроены в пазы, вырезанные в листах статора (рисунок ниже).
Однако для более крупных двигателей меньшая пульсация крутящего момента и более высокий КПД получаются, если катушки встроены в пазы, вырезанные в листах статора (рисунок ниже).
Рисунок 5.4 Корпус статора с прорезями для обмоток
Пластины статора представляют собой тонкие изолированные кольца с прорезями, выбитыми из листов электротехнической стали. Их стопка закреплена концевыми винтами, которые также могут удерживать концевые корпуса.
Рисунок 5.5 Статор с (a) 2-фазной и (b) 3-фазной обмотками
На приведенном выше рисунке обмотки двухфазного и трехфазного двигателей установлены в статоре. слоты. Катушки наматываются на внешнее приспособление, а затем вставляются в пазы. Изоляция, зажатая между периферией катушки и пазом, защищает от истирания. Реальные обмотки статора более сложны, чем отдельные обмотки на полюс на рисунке выше. Сравнивая двигатель 2-φ с двигателем Теслы 2-φ с явно выраженными полюсами, количество катушек такое же. В реальных больших двигателях полюсная обмотка разделена на одинаковые катушки, вставленные во множество меньших пазов, чем указано выше. Эта группа называется фазный ремень (см. рисунок ниже). Распределенные катушки фазового пояса подавляют некоторые нечетные гармоники, создавая более синусоидальное распределение магнитного поля поперек полюса. Это показано в разделе синхронного двигателя. Прорези на краю стержня могут иметь меньше витков, чем другие прорези. Краевые пазы могут содержать обмотки от двух фаз. То есть фазовые пояса перекрываются.
В реальных больших двигателях полюсная обмотка разделена на одинаковые катушки, вставленные во множество меньших пазов, чем указано выше. Эта группа называется фазный ремень (см. рисунок ниже). Распределенные катушки фазового пояса подавляют некоторые нечетные гармоники, создавая более синусоидальное распределение магнитного поля поперек полюса. Это показано в разделе синхронного двигателя. Прорези на краю стержня могут иметь меньше витков, чем другие прорези. Краевые пазы могут содержать обмотки от двух фаз. То есть фазовые пояса перекрываются.
Рисунок 5.6 Перекрытие фазных ремней
Ключом к популярности асинхронного двигателя переменного тока является его простота, о чем свидетельствует простой ротор (рисунок ниже). Ротор состоит из вала, стального ламинированного ротора и встроенной медной или алюминиевой пластины 9.Беличья клетка 0009 , показанная в (b), снята с ротора. По сравнению с якорем двигателя постоянного тока коллектор отсутствует. Это устраняет щетки, искрение, искрообразование, графитовую пыль, регулировку и замену щеток, а также повторную обработку коллектора.
Это устраняет щетки, искрение, искрообразование, графитовую пыль, регулировку и замену щеток, а также повторную обработку коллектора.
Рисунок 5.7 Многослойный ротор со встроенной (а) короткозамкнутой клеткой, (б) токопроводящей клеткой, снятой с ротора Несоосность с пазами статора снижает пульсации крутящего момента. Сердечники ротора и статора состоят из пакета изолированных пластин. Пластины покрыты изолирующим оксидом или лаком для минимизации потерь на вихревые токи. Сплав, используемый в пластинах, выбран из-за низких гистерезисных потерь.
Теория работы асинхронных двигателей
Краткое объяснение работы заключается в том, что статор создает вращающееся магнитное поле, которое притягивает ротор. Теория работы асинхронных двигателей основана на вращающемся магнитном поле. Одним из способов создания вращающегося магнитного поля является вращение постоянного магнита. Если движущиеся магнитные линии потока разрезают проводящий диск, он будет следовать за движением магнита. Линии потока, пересекающие проводник, будут индуцировать напряжение и, как следствие, протекание тока в проводящем диске. Этот поток тока создает электромагнит, полярность которого противоположна движению постоянного магнита.0009 Закон Ленца . Полярность электромагнита такова, что он притягивает постоянный магнит. Диск следует с немного меньшей скоростью, чем постоянный магнит.
Линии потока, пересекающие проводник, будут индуцировать напряжение и, как следствие, протекание тока в проводящем диске. Этот поток тока создает электромагнит, полярность которого противоположна движению постоянного магнита.0009 Закон Ленца . Полярность электромагнита такова, что он притягивает постоянный магнит. Диск следует с немного меньшей скоростью, чем постоянный магнит.
Рисунок 5.8 Вращающееся магнитное поле создает крутящий момент в проводящем диске
Вращающееся магнитное поле создает крутящий момент в проводящем диске
Крутящий момент, развиваемый диском, пропорционален количеству силовых линий, пересекающих диск, и скорости, с которой он пересекает диск . Если бы диск вращался с той же скоростью, что и постоянный магнит, не было бы ни потока, разрезающего диск, ни протекания индуцированного тока, ни электромагнитного поля, ни крутящего момента. Таким образом, скорость диска всегда будет отставать от скорости вращения постоянного магнита, так что линии потока, пересекающие диск, индуцируют ток, создают электромагнитное поле в диске, которое следует за постоянным магнитом. Если к диску приложена нагрузка, замедляющая его, будет развиваться больший крутящий момент, поскольку больше линий потока пересекает диск. Крутящий момент пропорционален скольжение , степень отставания диска от вращающегося магнита. Большее скольжение соответствует большему потоку, пересекающему проводящий диск, развивая больший крутящий момент. Аналоговый автомобильный вихретоковый спидометр основан на принципе, показанном выше. Когда диск удерживается пружиной, отклонение диска и иглы пропорционально скорости вращения магнита. Вращающееся магнитное поле создается двумя катушками, расположенными под прямым углом друг к другу, приводимыми в движение токами, которые сдвинуты по фазе на 90°. Это не должно вызывать удивления, если вы знакомы с паттернами Лиссажу на осциллографе.
Если к диску приложена нагрузка, замедляющая его, будет развиваться больший крутящий момент, поскольку больше линий потока пересекает диск. Крутящий момент пропорционален скольжение , степень отставания диска от вращающегося магнита. Большее скольжение соответствует большему потоку, пересекающему проводящий диск, развивая больший крутящий момент. Аналоговый автомобильный вихретоковый спидометр основан на принципе, показанном выше. Когда диск удерживается пружиной, отклонение диска и иглы пропорционально скорости вращения магнита. Вращающееся магнитное поле создается двумя катушками, расположенными под прямым углом друг к другу, приводимыми в движение токами, которые сдвинуты по фазе на 90°. Это не должно вызывать удивления, если вы знакомы с паттернами Лиссажу на осциллографе.
Рис. 5.9 В противофазе (90°) синусоидальные волны образуют круговую диаграмму Лиссажу горизонтальные и вертикальные входы осциллографа с синусоидальными волнами, сдвинутыми по фазе на 90°. Начиная с (а) с максимальным «X» и минимальным «Y» отклонением, трасса движется вверх и влево к (b). Между (a) и (b) два сигнала равны 0,707 Впик при 45°. Эта точка (0,707, 0,707) попадает на радиус окружности между (a) и (b). Трассировка движется к (b) с минимальным «X» и максимальным «Y» отклонением. При максимальном отрицательном «X» и минимальном отклонении «Y» трасса перемещается в (c). Затем с минимальным «X» и максимальным отрицательным «Y» он перемещается в (d) и обратно в (a), завершая один цикл.
Начиная с (а) с максимальным «X» и минимальным «Y» отклонением, трасса движется вверх и влево к (b). Между (a) и (b) два сигнала равны 0,707 Впик при 45°. Эта точка (0,707, 0,707) попадает на радиус окружности между (a) и (b). Трассировка движется к (b) с минимальным «X» и максимальным «Y» отклонением. При максимальном отрицательном «X» и минимальном отклонении «Y» трасса перемещается в (c). Затем с минимальным «X» и максимальным отрицательным «Y» он перемещается в (d) и обратно в (a), завершая один цикл.
Рисунок 5.10 Окружность синусоиды по оси X и косинуса по оси Y
На рисунке показаны две синусоидальные волны со сдвигом по фазе на 90°, воздействующие на отклоняющие пластины осциллографа, расположенные под прямым углом в пространстве. Комбинация синусоиды с фазой 90° и отклонения под прямым углом приводит к двумерному рисунку – кругу. Этот круг описывается электронным лучом, вращающимся против часовой стрелки.
Полная скорость двигателя и скорость синхронного двигателя
Скорость вращения магнитного поля статора связана с количеством пар полюсов на фазу статора. На приведенном ниже рисунке «полная скорость» всего шесть полюсов или три пары полюсов и три фазы. Однако на каждую фазу приходится только одна пара полюсов. Магнитное поле будет вращаться один раз за цикл синусоидальной волны. В случае мощности 60 Гц поле вращается со скоростью 60 раз в секунду или 3600 оборотов в минуту (об/мин). При мощности 50 Гц он вращается со скоростью 50 оборотов в секунду или 3000 об/мин. 3600 и 3000 об/мин — это синхронная скорость двигателя. Хотя ротор асинхронного двигателя никогда не достигает этой скорости, это, безусловно, верхний предел. Если мы удвоим количество полюсов двигателя, синхронная скорость уменьшится вдвое, потому что магнитное поле поворачивается на 180° в пространстве на 360° электрической синусоиды.
На приведенном ниже рисунке «полная скорость» всего шесть полюсов или три пары полюсов и три фазы. Однако на каждую фазу приходится только одна пара полюсов. Магнитное поле будет вращаться один раз за цикл синусоидальной волны. В случае мощности 60 Гц поле вращается со скоростью 60 раз в секунду или 3600 оборотов в минуту (об/мин). При мощности 50 Гц он вращается со скоростью 50 оборотов в секунду или 3000 об/мин. 3600 и 3000 об/мин — это синхронная скорость двигателя. Хотя ротор асинхронного двигателя никогда не достигает этой скорости, это, безусловно, верхний предел. Если мы удвоим количество полюсов двигателя, синхронная скорость уменьшится вдвое, потому что магнитное поле поворачивается на 180° в пространстве на 360° электрической синусоиды.
Рисунок 5.11 Удвоение полюсов статора вдвое уменьшает синхронную скорость
Синхронная скорость определяется как:
[latex]N_s = \frac{120 \cdot f}{P}[/latex]
Где:
N с = скорость магнитного поля (об/мин)
f = частота приложенной мощности (Гц)
P = общее количество полюсов на фазу, кратное 2
скорость» на рисунке выше имеет четыре полюса на фазу (3 фазы). Синхронная скорость для мощности 50 Гц составляет: S = 120·50/4 = 1500 об/мин
Синхронная скорость для мощности 50 Гц составляет: S = 120·50/4 = 1500 об/мин
Краткое объяснение асинхронного двигателя состоит в том, что вращающееся магнитное поле, создаваемое статором, тащит за собой ротор. Более длинное объяснение более правильное. заключается в том, что магнитное поле статора индуцирует переменный ток в проводниках короткозамкнутого ротора, которые составляют вторичную обмотку трансформатора. Этот индуцированный ток ротора, в свою очередь, создает магнитное поле. Магнитное поле вращающегося статора взаимодействует с этим полем ротора. Поле ротора пытается выровняться с вращающимся полем статора. Результатом является вращение короткозамкнутого ротора. Если бы не было механической нагрузки крутящего момента двигателя, подшипников, аэродинамических или других потерь, ротор вращался бы с синхронной скоростью. Тем не менее, проскальзывание между ротором и полем статора синхронной скорости развивает крутящий момент. Именно магнитный поток, разрезающий проводники ротора при его проскальзывании, создает крутящий момент. Таким образом, нагруженный двигатель будет проскальзывать пропорционально механической нагрузке. Если бы ротор вращался с синхронной скоростью, не было бы ни потока статора, разрезающего ротор, ни тока, индуцируемого в роторе, ни крутящего момента.
Таким образом, нагруженный двигатель будет проскальзывать пропорционально механической нагрузке. Если бы ротор вращался с синхронной скоростью, не было бы ни потока статора, разрезающего ротор, ни тока, индуцируемого в роторе, ни крутящего момента.
Крутящий момент в асинхронных двигателях
Когда на двигатель впервые подается питание, ротор находится в состоянии покоя, а магнитное поле статора вращается с синхронной скоростью N с . Поле статора режет ротор с синхронной скоростью N s . Ток, наведенный в короткозамкнутых витках ротора, максимален, как и частота тока, частота сети. По мере увеличения скорости ротора скорость, с которой поток статора пересекает ротор, представляет собой разницу между синхронной скоростью N с и фактической скоростью вращения ротора N, или (N с – N). Отношение фактического потока, обрезающего ротор, к синхронной скорости определяется как скольжение :
.
[латекс]s = \frac{(N_s — N)}{N_s}[/latex]
Где:
N с = синхронная скорость
N = скорость ротора
Частота тока, индуцированного в проводниках ротора, равна частоте сети при пуске двигателя и уменьшается по мере приближения ротора к синхронной скорости. Частота ротора определяется как:
Частота ротора определяется как:
[латекс]f_r = с \cdot f[/латекс]
Где:
с = скольжение,
f = частота питающей сети статора
Проскальзывание при 100 % крутящего момента обычно составляет 5 % или менее в асинхронных двигателях. Таким образом, для частоты сети f = 50 Гц частота наведенного тока в роторе:
f r = S(f )
= 0,05 (50 Гц)
= 2,5 Гц.
Почему так мало? Магнитное поле статора вращается с частотой 50 Гц. Скорость ротора меньше на 5%. Вращающееся магнитное поле режет ротор только на частоте 2,5 Гц. 2,5 Гц — это разница между синхронной скоростью и фактической скоростью вращения ротора. Если ротор будет вращаться немного быстрее, на синхронной скорости, никакой поток вообще не перережет ротор, f r = 0,
Рисунок 5.12 Крутящий момент и скорость в зависимости от % скольжения.
На приведенном выше графике показано, что пусковой момент, известный как крутящий момент при заблокированном роторе (T LR ), превышает 100 % крутящего момента при полной нагрузке (T FL ), безопасного постоянного крутящего момента. Крутящий момент заблокированного ротора составляет около 175% от T FL для приведенного выше примера двигателя. Пусковой ток, известный как ток блокировки ротора (I LR ), составляет 500% от ток полной нагрузки (I FL ), безопасный рабочий ток. Ток высокий, потому что это аналогично закороченной вторичной обмотке трансформатора. Когда ротор начинает вращаться, крутящий момент может немного уменьшиться для определенных классов двигателей до значения, известного как подтягивающий момент . Это самое низкое значение крутящего момента, с которым когда-либо сталкивался пусковой двигатель. Когда ротор набирает 80 % синхронной скорости, крутящий момент увеличивается со 175 % до 300 % крутящего момента при полной нагрузке. Это пробивной момент (T BD ) возникает из-за большего, чем обычно, 20% проскальзывания. Ток уменьшился лишь незначительно в этой точке, но будет быстро уменьшаться после этой точки. Когда ротор разгоняется до нескольких процентов от синхронной скорости, крутящий момент и ток существенно уменьшаются.
Крутящий момент заблокированного ротора составляет около 175% от T FL для приведенного выше примера двигателя. Пусковой ток, известный как ток блокировки ротора (I LR ), составляет 500% от ток полной нагрузки (I FL ), безопасный рабочий ток. Ток высокий, потому что это аналогично закороченной вторичной обмотке трансформатора. Когда ротор начинает вращаться, крутящий момент может немного уменьшиться для определенных классов двигателей до значения, известного как подтягивающий момент . Это самое низкое значение крутящего момента, с которым когда-либо сталкивался пусковой двигатель. Когда ротор набирает 80 % синхронной скорости, крутящий момент увеличивается со 175 % до 300 % крутящего момента при полной нагрузке. Это пробивной момент (T BD ) возникает из-за большего, чем обычно, 20% проскальзывания. Ток уменьшился лишь незначительно в этой точке, но будет быстро уменьшаться после этой точки. Когда ротор разгоняется до нескольких процентов от синхронной скорости, крутящий момент и ток существенно уменьшаются. Проскальзывание будет составлять всего несколько процентов при нормальной работе. Для работающего двигателя любая часть кривой крутящего момента ниже 100 % номинального крутящего момента является нормальной. Нагрузка двигателя определяет рабочую точку на кривой крутящего момента. В то время как крутящий момент и ток двигателя могут превышать 100 % в течение нескольких секунд во время запуска, непрерывная работа при превышении 100 % может привести к повреждению двигателя. Любая нагрузка по крутящему моменту двигателя выше предельного крутящего момента приведет к остановке двигателя. Крутящий момент, скольжение и ток будут приближаться к нулю для состояния нагрузки «отсутствие механического крутящего момента». Это состояние аналогично открытому вторичному трансформатору. Существует несколько основных конструкций асинхронных двигателей, демонстрирующих значительные отклонения от приведенной выше кривой крутящего момента. Различные конструкции оптимизированы для запуска и работы с различными типами нагрузок.
Проскальзывание будет составлять всего несколько процентов при нормальной работе. Для работающего двигателя любая часть кривой крутящего момента ниже 100 % номинального крутящего момента является нормальной. Нагрузка двигателя определяет рабочую точку на кривой крутящего момента. В то время как крутящий момент и ток двигателя могут превышать 100 % в течение нескольких секунд во время запуска, непрерывная работа при превышении 100 % может привести к повреждению двигателя. Любая нагрузка по крутящему моменту двигателя выше предельного крутящего момента приведет к остановке двигателя. Крутящий момент, скольжение и ток будут приближаться к нулю для состояния нагрузки «отсутствие механического крутящего момента». Это состояние аналогично открытому вторичному трансформатору. Существует несколько основных конструкций асинхронных двигателей, демонстрирующих значительные отклонения от приведенной выше кривой крутящего момента. Различные конструкции оптимизированы для запуска и работы с различными типами нагрузок. Крутящий момент заблокированного ротора (T LR ) для двигателей различных конструкций и размеров в диапазоне от 60% до 350% крутящего момента при полной нагрузке (T FL ). Пусковой ток или ток блокировки ротора (I LR ) может составлять от 500% до 1400% тока полной нагрузки (I FL ). Это потребление тока может представлять проблему для запуска больших асинхронных двигателей.
Крутящий момент заблокированного ротора (T LR ) для двигателей различных конструкций и размеров в диапазоне от 60% до 350% крутящего момента при полной нагрузке (T FL ). Пусковой ток или ток блокировки ротора (I LR ) может составлять от 500% до 1400% тока полной нагрузки (I FL ). Это потребление тока может представлять проблему для запуска больших асинхронных двигателей.
Классы двигателей NEMA и IEC
Различные стандартные классы (или конструкции) для двигателей, соответствующие кривым крутящего момента (рисунок ниже), были разработаны для лучшего управления различными типами нагрузок. Национальная ассоциация производителей электрооборудования (NEMA) определила классы двигателей A, B, C и D для соответствия этим требованиям привода. Аналогичные классы N и H Международной электротехнической комиссии (МЭК) соответствуют конструкциям NEMA B и C соответственно.
Рисунок 5.13 Характеристики конструкций NEMA
Характеристики конструкций NEMA
Все двигатели, кроме класса D, работают с проскальзыванием 5 % или менее при полной нагрузке.
- Класс B (IEC Класс N) двигатели по умолчанию используются в большинстве приложений. При пусковом моменте LRT = от 150% до 170% FLT он может запускать большинство нагрузок без чрезмерного пускового тока (LRT). КПД и коэффициент мощности высокие. Обычно он приводит в действие насосы, вентиляторы и станки.
- Класс A Пусковой крутящий момент такой же, как у класса B. Отпускной крутящий момент и пусковой ток (LRT) выше. Этот двигатель справляется с кратковременными перегрузками, которые встречаются в машинах для литья под давлением.
- Класс C (IEC Класс H) имеет более высокий пусковой крутящий момент, чем классы A и B, при LRT = 200 % от FLT. Этот двигатель применяется для нагрузок с жестким пуском, которые должны приводиться в движение с постоянной скоростью, таких как конвейеры, дробилки, поршневые насосы и компрессоры.
- 9Двигатели 0230 класса D имеют самый высокий пусковой момент (LRT) в сочетании с низким пусковым током из-за высокого скольжения (от 5% до 13% при FLT).
 Большое скольжение приводит к снижению скорости. Регулировка скорости плохая. Тем не менее, двигатель отлично справляется с нагрузками с высокой переменной скоростью, такими как те, для которых требуется маховик с накоплением энергии. Области применения включают штамповочные прессы, ножницы и элеваторы.
Большое скольжение приводит к снижению скорости. Регулировка скорости плохая. Тем не менее, двигатель отлично справляется с нагрузками с высокой переменной скоростью, такими как те, для которых требуется маховик с накоплением энергии. Области применения включают штамповочные прессы, ножницы и элеваторы. - Электродвигатели класса E представляют собой более эффективную версию класса B.
- Двигатели класса F имеют гораздо более низкие LRC, LRT и пусковой момент, чем класс B. Они управляют постоянными, легко запускаемыми нагрузками.
Коэффициент мощности асинхронных двигателей
Асинхронные двигатели имеют отстающий (индуктивный) коэффициент мощности по отношению к линии электропередачи. Коэффициент мощности в больших полностью нагруженных высокоскоростных двигателях может достигать 90 % для больших высокоскоростных двигателей. При 3/4 полной нагрузки максимальный коэффициент мощности высокоскоростного двигателя может составлять 92%. Коэффициент мощности для небольших тихоходных двигателей может составлять всего 50 %. При пуске коэффициент мощности может находиться в диапазоне от 10% до 25%, увеличиваясь по мере того, как ротор достигает скорости. Коэффициент мощности (PF) значительно зависит от механической нагрузки двигателя (рисунок ниже). Ненагруженный двигатель аналогичен трансформатору без резистивной нагрузки на вторичной обмотке. Небольшое сопротивление отражается от вторичной обмотки (ротор) к первичной обмотке (статор). Таким образом, линия электропередач испытывает реактивную нагрузку всего 10% PF. Когда ротор нагружается, увеличивающаяся резистивная составляющая отражается от ротора к статору, увеличивая коэффициент мощности.
Коэффициент мощности для небольших тихоходных двигателей может составлять всего 50 %. При пуске коэффициент мощности может находиться в диапазоне от 10% до 25%, увеличиваясь по мере того, как ротор достигает скорости. Коэффициент мощности (PF) значительно зависит от механической нагрузки двигателя (рисунок ниже). Ненагруженный двигатель аналогичен трансформатору без резистивной нагрузки на вторичной обмотке. Небольшое сопротивление отражается от вторичной обмотки (ротор) к первичной обмотке (статор). Таким образом, линия электропередач испытывает реактивную нагрузку всего 10% PF. Когда ротор нагружается, увеличивающаяся резистивная составляющая отражается от ротора к статору, увеличивая коэффициент мощности.
Рисунок 5.14 Коэффициент мощности и КПД асинхронного двигателя
КПД асинхронных двигателей
Большие трехфазные двигатели более эффективны, чем трехфазные двигатели меньшего размера, и почти все однофазные двигатели. КПД большого асинхронного двигателя может достигать 95% при полной нагрузке, хотя чаще встречается 90%. КПД слабонагруженного или ненагруженного асинхронного двигателя низкий, поскольку большая часть тока приходится на поддержание намагничивающего потока. По мере увеличения нагрузки по крутящему моменту для создания крутящего момента потребляется больше тока, в то время как ток, связанный с намагничиванием, остается постоянным. Эффективность при 75% FLT может быть немного выше, чем при 100% FLT. Эффективность снижается на несколько процентов при 50% FLT и еще на несколько процентов при 25% FLT. Эффективность становится плохой только ниже 25% FLT. Изменение КПД в зависимости от нагрузки показано на рисунке выше. Асинхронные двигатели обычно имеют увеличенный размер, чтобы гарантировать, что их механическая нагрузка может запускаться и приводиться в действие при любых условиях эксплуатации. Если многофазный двигатель нагружается при крутящем моменте менее 75 % от номинального, когда КПД достигает пика, эффективность снижается лишь незначительно до 25 % FLT.
КПД слабонагруженного или ненагруженного асинхронного двигателя низкий, поскольку большая часть тока приходится на поддержание намагничивающего потока. По мере увеличения нагрузки по крутящему моменту для создания крутящего момента потребляется больше тока, в то время как ток, связанный с намагничиванием, остается постоянным. Эффективность при 75% FLT может быть немного выше, чем при 100% FLT. Эффективность снижается на несколько процентов при 50% FLT и еще на несколько процентов при 25% FLT. Эффективность становится плохой только ниже 25% FLT. Изменение КПД в зависимости от нагрузки показано на рисунке выше. Асинхронные двигатели обычно имеют увеличенный размер, чтобы гарантировать, что их механическая нагрузка может запускаться и приводиться в действие при любых условиях эксплуатации. Если многофазный двигатель нагружается при крутящем моменте менее 75 % от номинального, когда КПД достигает пика, эффективность снижается лишь незначительно до 25 % FLT.
Корректор коэффициента мощности Nola
Франк Нола из НАСА предложил корректор коэффициента мощности (PFC) в качестве энергосберегающего устройства для однофазных асинхронных двигателей в конце 1970-х годов. Он основан на предположении, что асинхронный двигатель с неполной нагрузкой менее эффективен и имеет более низкий коэффициент мощности, чем двигатель с полной нагрузкой. Таким образом, в двигателях с частичной нагрузкой, в частности, в двигателях 1-φ, необходимо экономить энергию. Энергия, потребляемая для поддержания магнитного поля статора, относительно постоянна по отношению к изменениям нагрузки. В то время как в полностью нагруженном двигателе нечего экономить, напряжение на частично нагруженном двигателе может быть уменьшено, чтобы уменьшить энергию, необходимую для поддержания магнитного поля. Это повысит коэффициент мощности и КПД. Это была хорошая концепция для общеизвестно неэффективных однофазных двигателей, для которых она предназначалась. Эта концепция не очень применима к большим трехфазным двигателям. Из-за их высокой эффективности (90%+), экономия энергии невелика. Более того, двигатель с КПД 95 % по-прежнему имеет КПД 94 % при 50 % крутящего момента при полной нагрузке (FLT) и КПД 90 % при 25 % FLT.
Он основан на предположении, что асинхронный двигатель с неполной нагрузкой менее эффективен и имеет более низкий коэффициент мощности, чем двигатель с полной нагрузкой. Таким образом, в двигателях с частичной нагрузкой, в частности, в двигателях 1-φ, необходимо экономить энергию. Энергия, потребляемая для поддержания магнитного поля статора, относительно постоянна по отношению к изменениям нагрузки. В то время как в полностью нагруженном двигателе нечего экономить, напряжение на частично нагруженном двигателе может быть уменьшено, чтобы уменьшить энергию, необходимую для поддержания магнитного поля. Это повысит коэффициент мощности и КПД. Это была хорошая концепция для общеизвестно неэффективных однофазных двигателей, для которых она предназначалась. Эта концепция не очень применима к большим трехфазным двигателям. Из-за их высокой эффективности (90%+), экономия энергии невелика. Более того, двигатель с КПД 95 % по-прежнему имеет КПД 94 % при 50 % крутящего момента при полной нагрузке (FLT) и КПД 90 % при 25 % FLT. Потенциальная экономия энергии при переходе от 100 % FLT к 25 % FLT представляет собой разницу в эффективности 95 % – 90 % = 5 %. Это не 5% мощности при полной нагрузке, а 5% мощности при пониженной нагрузке. Корректор коэффициента мощности Nola может быть применим к 3-фазному двигателю, который большую часть времени работает на холостом ходу (ниже 25% FLT), например, к штамповочному прессу. Срок окупаемости дорогого электронного контроллера оценивается как непривлекательный для большинства приложений. Тем не менее, он может быть экономичным как часть электронного пускателя двигателя или регулятора скорости. Асинхронный двигатель может работать как генератор переменного тока, если он является приводом 9.0003
Потенциальная экономия энергии при переходе от 100 % FLT к 25 % FLT представляет собой разницу в эффективности 95 % – 90 % = 5 %. Это не 5% мощности при полной нагрузке, а 5% мощности при пониженной нагрузке. Корректор коэффициента мощности Nola может быть применим к 3-фазному двигателю, который большую часть времени работает на холостом ходу (ниже 25% FLT), например, к штамповочному прессу. Срок окупаемости дорогого электронного контроллера оценивается как непривлекательный для большинства приложений. Тем не менее, он может быть экономичным как часть электронного пускателя двигателя или регулятора скорости. Асинхронный двигатель может работать как генератор переменного тока, если он является приводом 9.0003
Асинхронные двигатели в качестве генераторов переменного тока
Асинхронный двигатель может работать как генератор переменного тока, если он приводится в действие крутящим моментом, превышающим 100% синхронной скорости (рисунок ниже). Это соответствует нескольким процентам «отрицательного» скольжения, скажем, -1%. Это означает, что, поскольку мы вращаем двигатель быстрее, чем синхронная скорость, ротор движется на 1% быстрее, чем магнитное поле статора. Обычно он отстает на 1% в двигателе. Поскольку ротор пересекает магнитное поле статора в противоположном направлении (вперед), ротор индуцирует напряжение в статоре, возвращая электрическую энергию обратно в линию электропередачи.
Это означает, что, поскольку мы вращаем двигатель быстрее, чем синхронная скорость, ротор движется на 1% быстрее, чем магнитное поле статора. Обычно он отстает на 1% в двигателе. Поскольку ротор пересекает магнитное поле статора в противоположном направлении (вперед), ротор индуцирует напряжение в статоре, возвращая электрическую энергию обратно в линию электропередачи.
Рисунок 5.15 Отрицательный крутящий момент превращает асинхронный двигатель в генератор
Такой асинхронный генератор должен возбуждаться от «живого» источника питания с частотой 50 или 60 Гц. Энергия не может быть произведена в случае сбоя питания энергетической компании. Этот тип генератора переменного тока не подходит в качестве резервного источника питания. В качестве генератора ветряной турбины вспомогательной мощности он имеет то преимущество, что не требует автоматического выключателя отключения питания для защиты ремонтных бригад. Это отказоустойчиво.
Небольшие удаленные (от электросети) установки можно сделать самовозбуждающимися путем размещения конденсаторов параллельно фазам статора. Если нагрузка удалена, остаточный магнетизм может генерировать небольшой ток. Этот ток может протекать через конденсаторы без рассеивания мощности. Когда генератор разгоняется до полной скорости, ток увеличивается, чтобы обеспечить ток намагничивания статора. В этот момент можно приложить нагрузку. Регулировка напряжения плохая. Асинхронный двигатель можно преобразовать в генератор с самовозбуждением путем добавления конденсаторов.
Если нагрузка удалена, остаточный магнетизм может генерировать небольшой ток. Этот ток может протекать через конденсаторы без рассеивания мощности. Когда генератор разгоняется до полной скорости, ток увеличивается, чтобы обеспечить ток намагничивания статора. В этот момент можно приложить нагрузку. Регулировка напряжения плохая. Асинхронный двигатель можно преобразовать в генератор с самовозбуждением путем добавления конденсаторов.
Процедура запуска заключается в разгоне ветряной турбины до скорости в моторном режиме путем подачи на статор нормального сетевого напряжения. Любая скорость турбины, вызванная ветром, превышающая синхронную скорость, будет развивать отрицательный крутящий момент, возвращая мощность обратно в линию электропередачи, изменяя нормальное направление электрического счетчика киловатт-часов. В то время как асинхронный двигатель имеет отстающий коэффициент мощности от линии электропередачи, асинхронный генератор переменного тока имеет опережающий коэффициент мощности. Асинхронные генераторы не нашли широкого применения в обычных электростанциях. Скорость привода паровой турбины постоянна и регулируется в соответствии с требованиями синхронных генераторов переменного тока. Синхронные генераторы также более эффективны.
Асинхронные генераторы не нашли широкого применения в обычных электростанциях. Скорость привода паровой турбины постоянна и регулируется в соответствии с требованиями синхронных генераторов переменного тока. Синхронные генераторы также более эффективны.
Скорость ветряной турбины трудно контролировать, и она зависит от порывов ветра. Индукционный генератор лучше справляется с этими изменениями из-за присущего ему проскальзывания. Это нагружает зубчатую передачу и механические компоненты меньше, чем синхронный генератор. Однако это допустимое изменение скорости составляет всего около 1%. Таким образом, асинхронный генератор с прямым подключением к сети считается ветровой турбиной с фиксированной скоростью (см. «Асинхронный генератор с двойным питанием» для истинного генератора переменного тока с переменной скоростью). Несколько генераторов или несколько обмоток на общем валу можно переключать, чтобы обеспечить высокую и низкую скорость, чтобы приспособиться к переменным ветровым условиям.
Асинхронные двигатели с несколькими возбуждениями
Асинхронные двигатели могут содержать несколько обмоток возбуждения, например, 4-полюсную и 8-полюсную обмотки, соответствующие синхронным скоростям 1800 и 900 об/мин. Активация того или иного поля менее сложна, чем перемонтаж катушек статора.
Рисунок 5.16 Несколько полей позволяют изменять скорость
Если поле сегментировано с выведенными выводами, его можно пересоединить (или переключить) с 4-полюсного на 2-полюсное, как показано выше для 2-фазного двигателя. Сегменты 22,5° можно переключать на сегменты 45°. Для ясности выше показано подключение только одной фазы. Таким образом, наш асинхронный двигатель может работать на нескольких скоростях. При переключении вышеупомянутого двигателя частотой 60 Гц с 4 полюсов на 2 полюса синхронная скорость увеличивается с 1800 об/мин до 3600 об/мин.
Q: Если двигатель приводится в действие с частотой 50 Гц, каковы будут соответствующие 4-полюсные и 2-полюсные синхронные скорости?
A:
[латекс]N_s = \frac{120f}{P}[/latex] [латекс]N_s = \frac{120*50 Гц}{4}[/latex] [латекс]= 1500 об/мин (4-полюсный)[/латекс]
[латекс]N_s = \frac{120f}{P}[/latex] [латекс]N_s = \frac{120*50 Гц}{2}[/latex] [латекс]= 3000 об/мин (2-полюсный)[/латекс]
Асинхронные двигатели с регулируемым напряжением
Скорость малых асинхронных двигателей с короткозамкнутым ротором для таких приложений, как привод вентиляторов, может быть изменена путем снижения сетевого напряжения. Это уменьшает крутящий момент, доступный для нагрузки, что снижает скорость (см. рисунок ниже).
Это уменьшает крутящий момент, доступный для нагрузки, что снижает скорость (см. рисунок ниже).
Рисунок 5.17 Регулятор переменного напряжения управляет скоростью асинхронного двигателя
Электронное управление скоростью в асинхронных двигателях
Современная полупроводниковая электроника расширяет возможности управления скоростью. Изменяя частоту сети 50 или 60 Гц на более высокие или более низкие значения, можно изменить синхронную скорость двигателя. Однако уменьшение частоты тока, подаваемого на двигатель, также уменьшает реактивное сопротивление X L что увеличивает ток статора. Это может привести к насыщению магнитной цепи статора с катастрофическими последствиями. На практике напряжение на двигателе необходимо уменьшать при снижении частоты.
Рисунок 5.18 Электронный преобразователь частоты
И наоборот, частота привода может быть увеличена для увеличения синхронной скорости двигателя. Однако напряжение необходимо увеличить, чтобы преодолеть увеличивающееся реактивное сопротивление, чтобы поддерживать ток на нормальном уровне и поддерживать крутящий момент. Инвертор приближает синусоидальные волны к двигателю с выходами широтно-импульсной модуляции. Это обрезанная форма волны, которая либо включена, либо выключена, имеет высокий или низкий уровень, процент времени «включения» соответствует мгновенному напряжению синусоидальной волны.
Инвертор приближает синусоидальные волны к двигателю с выходами широтно-импульсной модуляции. Это обрезанная форма волны, которая либо включена, либо выключена, имеет высокий или низкий уровень, процент времени «включения» соответствует мгновенному напряжению синусоидальной волны.
Когда электроника применяется для управления асинхронным двигателем, становится доступным множество методов управления, от простых до сложных:
- Скалярное управление: Недорогой метод, описанный выше, для управления только напряжением и частотой без обратной связи.
- Векторное управление: Также известно как векторное фазовое управление. Компоненты тока статора, создающие поток и крутящий момент, измеряются или оцениваются в режиме реального времени, чтобы улучшить кривую скорости вращения двигателя. Это требует интенсивных вычислений.
- Прямое управление крутящим моментом: Продуманная адаптивная модель двигателя обеспечивает более прямое управление потоком и крутящим моментом без обратной связи.
 Этот метод быстро реагирует на изменение нагрузки.
Этот метод быстро реагирует на изменение нагрузки.
- Многофазный асинхронный двигатель состоит из многофазной обмотки, встроенной в многослойный статор, и проводящей короткозамкнутой клетки, встроенной в многослойный ротор.
- Трехфазные токи, протекающие внутри статора, создают вращающееся магнитное поле, которое индуцирует ток и, как следствие, магнитное поле в роторе. Крутящий момент ротора развивается, когда ротор немного проскальзывает за вращающимся полем статора.
- В отличие от однофазных двигателей, многофазные асинхронные двигатели запускаются автоматически.
- Пускатели двигателей минимизируют нагрузку на линию электропередачи, обеспечивая при этом больший пусковой момент, чем требуется во время работы. Редукторы линейного тока пускатели требуются только для больших двигателей.
- Трехфазные двигатели будут работать на одной фазе, если они запущены.
- Статический преобразователь фаз – это трехфазный двигатель, работающий от одной фазы без нагрузки на валу и создающий трехфазный выходной сигнал.

- Несколько обмоток возбуждения можно перемонтировать для нескольких дискретных скоростей двигателя путем изменения количества полюсов.
Трехфазный двигатель может работать от однофазного источника питания. Однако он не запустится самостоятельно. Его можно запускать вручную в любом направлении, набирая скорость за несколько секунд. Он будет развивать только 2/3 номинальной мощности 3-φ, потому что одна обмотка не используется.
Рисунок 5.19 Двигатель 3-φ работает от мощности 1-φ, но не запускается
Одиночная катушка однофазного двигателя
Одна катушка однофазного асинхронного двигателя создает не вращающееся магнитное поле, а пульсирующее поле, достигающее максимальной интенсивности при 0° и 180° электрического поля.
Рисунок 5.20 Однофазный статор создает невращающееся пульсирующее магнитное поле
Другая точка зрения состоит в том, что одиночная катушка, возбуждаемая однофазным током, создает два вектора магнитного поля, вращающихся в противоположных направлениях, совпадающих дважды за оборот при 0° ( Рисунок выше-а) и 180° (рисунок д). Когда вектора поворачиваются на 90° и -90° они сокращаются на рисунке c. При углах 45° и -45° (рисунок b) они частично складываются по оси +x и компенсируются по оси y. Аналогичная ситуация существует на рисунке d. Сумма этих двух векторов представляет собой вектор, стационарный в пространстве, но меняющий полярность во времени. Таким образом, пусковой момент не развивается.
Когда вектора поворачиваются на 90° и -90° они сокращаются на рисунке c. При углах 45° и -45° (рисунок b) они частично складываются по оси +x и компенсируются по оси y. Аналогичная ситуация существует на рисунке d. Сумма этих двух векторов представляет собой вектор, стационарный в пространстве, но меняющий полярность во времени. Таким образом, пусковой момент не развивается.
Однако, если ротор вращается вперед со скоростью, немного меньшей синхронной скорости, он будет развивать максимальный крутящий момент при 10% скольжении по отношению к вектору прямого вращения. Меньший крутящий момент будет развиваться выше или ниже 10% скольжения. Ротор будет иметь проскальзывание 200–10 % относительно вектора магнитного поля, вращающегося в противоположных направлениях. Небольшой крутящий момент (см. кривую крутящего момента в зависимости от скольжения), кроме двухчастотной пульсации, возникает из-за вращения вектора в противоположных направлениях. Таким образом, однофазная катушка будет развивать крутящий момент после запуска ротора. Если ротор запустить в обратном направлении, он будет развивать такой же большой крутящий момент, когда он приближается к скорости обратного вращения вектора.
Если ротор запустить в обратном направлении, он будет развивать такой же большой крутящий момент, когда он приближается к скорости обратного вращения вектора.
Однофазные асинхронные двигатели имеют медную или алюминиевую короткозамкнутую клетку, встроенную в цилиндр из стальных пластин, типичный для многофазных асинхронных двигателей.
Двигатель с постоянно разделенным конденсатором
Одним из способов решения проблемы однофазного двигателя является создание двухфазного двигателя, получающего двухфазное питание от однофазного. Для этого требуется двигатель с двумя обмотками, разнесенными на 90 90 230 ° 90 231 , питаемый двумя фазами тока, смещенными во времени на 90 90 230 ° 90 231 . Это называется двигателем с постоянно разделенным конденсатором.
Рисунок 5.21 Асинхронный двигатель с постоянно разделенными конденсаторами
Асинхронный двигатель с постоянными конденсаторами с разделенными конденсаторами
В этом типе двигателя наблюдается повышенная величина тока и сдвиг во времени назад, когда двигатель достигает скорости, с пульсациями крутящего момента на полной скорости. Решение состоит в том, чтобы конденсатор (сопротивление) был небольшим, чтобы минимизировать потери. Потери меньше, чем для двигателя с расщепленными полюсами. Эта конфигурация двигателя хорошо работает до 1/4 лошадиных сил (200 Вт), хотя обычно применяется к двигателям меньшего размера. Направление двигателя легко изменить, включив конденсатор последовательно с другой обмоткой. Этот тип двигателя может быть адаптирован для использования в качестве серводвигателя, описанного в другом месте этой главы.
Решение состоит в том, чтобы конденсатор (сопротивление) был небольшим, чтобы минимизировать потери. Потери меньше, чем для двигателя с расщепленными полюсами. Эта конфигурация двигателя хорошо работает до 1/4 лошадиных сил (200 Вт), хотя обычно применяется к двигателям меньшего размера. Направление двигателя легко изменить, включив конденсатор последовательно с другой обмоткой. Этот тип двигателя может быть адаптирован для использования в качестве серводвигателя, описанного в другом месте этой главы.
Рисунок 5.22 Однофазный асинхронный двигатель со встроенными катушками статора
Однофазные асинхронные двигатели могут иметь катушки, встроенные в статор для двигателей большего размера. Тем не менее, меньшие размеры используют менее сложные для создания сосредоточенных обмоток с выступающими полюсами.
Асинхронный двигатель с пусковым конденсатором
На приведенном ниже рисунке для запуска однофазного асинхронного двигателя через вспомогательную обмотку можно использовать конденсатор большей емкости, если он отключается центробежным выключателем после того, как двигатель разогнался до нужной скорости. Кроме того, вспомогательная обмотка может состоять из гораздо большего количества витков более толстого провода, чем используется в двигателе с расщепленной фазой сопротивления, чтобы смягчить чрезмерное повышение температуры. В результате для тяжелых нагрузок, таких как компрессоры кондиционера, доступен больший пусковой крутящий момент. Эта конфигурация двигателя работает настолько хорошо, что доступна в размерах с несколькими лошадиными силами (несколько киловатт).
Кроме того, вспомогательная обмотка может состоять из гораздо большего количества витков более толстого провода, чем используется в двигателе с расщепленной фазой сопротивления, чтобы смягчить чрезмерное повышение температуры. В результате для тяжелых нагрузок, таких как компрессоры кондиционера, доступен больший пусковой крутящий момент. Эта конфигурация двигателя работает настолько хорошо, что доступна в размерах с несколькими лошадиными силами (несколько киловатт).
Рисунок 5.23 Асинхронный двигатель с конденсаторным пуском
Асинхронный двигатель с конденсаторным пуском
Вариант двигателя с пусковым конденсатором (рис. номинальный конденсатор на месте после пуска для улучшения рабочих характеристик без чрезмерного потребления тока. Дополнительная сложность двигателя с конденсаторным приводом оправдана для двигателей большего размера.
Рисунок 5.24 Асинхронный двигатель с конденсаторным двигателем
Пусковой конденсатор двигателя может быть двуханодным неполярным электролитическим конденсатором, который может состоять из двух последовательно соединенных полярных электролитических конденсаторов + к + (или – к -). Такие электролитические конденсаторы, рассчитанные на переменный ток, имеют настолько высокие потери, что их можно использовать только в повторно-кратковременном режиме (1 секунда включена, 60 секунд выключена), например при запуске двигателя. Конденсатор для работы двигателя должен быть не электролитического, а полимерного типа с меньшими потерями.
Такие электролитические конденсаторы, рассчитанные на переменный ток, имеют настолько высокие потери, что их можно использовать только в повторно-кратковременном режиме (1 секунда включена, 60 секунд выключена), например при запуске двигателя. Конденсатор для работы двигателя должен быть не электролитического, а полимерного типа с меньшими потерями.
Асинхронный двигатель с расщепленной фазой сопротивления
Если во вспомогательной обмотке намного меньше витков, меньший провод расположен под углом 90 90 230 ° 90 231 к основной обмотке, он может запустить однофазный асинхронный двигатель. При более низкой индуктивности и более высоком сопротивлении ток будет испытывать меньший фазовый сдвиг, чем основная обмотка. Можно получить около 30 90 230 ° 90 231 разности фаз. Эта катушка создает умеренный пусковой момент, который отключается центробежным выключателем на 3/4 синхронной скорости. Эта простая схема (без конденсатора) хорошо подходит для двигателей мощностью до 1/3 лошадиных сил (250 Вт), приводящих в движение легко запускаемые нагрузки.
Рисунок 5.25 Асинхронный двигатель с расщепленной фазой сопротивления
Этот двигатель имеет больший пусковой момент, чем двигатель с расщепленными полюсами (следующий раздел), но не такой большой, как двухфазный двигатель, собранный из тех же деталей. Плотность тока во вспомогательной обмотке во время пуска настолько высока, что последующее быстрое повышение температуры исключает частые повторные пуски или медленные пусковые нагрузки.
Корректор коэффициента мощности Nola
Франк Нола из НАСА предложил корректор коэффициента мощности для повышения эффективности асинхронных двигателей переменного тока в середине 19-го века.70-е годы. Он основан на предположении, что асинхронные двигатели неэффективны при меньшей нагрузке, чем полная. Эта неэффективность коррелирует с низким коэффициентом мощности. Коэффициент мощности меньше единицы из-за тока намагничивания, необходимого статору. Этот фиксированный ток составляет большую долю от общего тока двигателя по мере уменьшения нагрузки двигателя. При малой нагрузке полный ток намагничивания не требуется. Его можно уменьшить, уменьшив приложенное напряжение, улучшив коэффициент мощности и эффективность. Корректор коэффициента мощности определяет коэффициент мощности и снижает напряжение двигателя, тем самым восстанавливая более высокий коэффициент мощности и уменьшая потери.
При малой нагрузке полный ток намагничивания не требуется. Его можно уменьшить, уменьшив приложенное напряжение, улучшив коэффициент мощности и эффективность. Корректор коэффициента мощности определяет коэффициент мощности и снижает напряжение двигателя, тем самым восстанавливая более высокий коэффициент мощности и уменьшая потери.
Поскольку однофазные двигатели примерно в 2-4 раза менее эффективны, чем трехфазные двигатели, для двигателей 1-φ существует потенциальная экономия энергии. Для полностью нагруженного двигателя нет экономии, поскольку требуется весь ток намагничивания статора. Напряжение не может быть снижено. Но есть потенциальная экономия от менее чем полностью загруженного двигателя. Двигатель с номинальным напряжением 117 В переменного тока рассчитан на работу при напряжении от 127 до 104 В переменного тока. Это означает, что он не полностью загружен при работе от напряжения выше 104 В переменного тока, например, холодильник на 117 В переменного тока. Для регулятора коэффициента мощности безопасно снизить напряжение сети до 104–110 В переменного тока. Чем выше начальное линейное напряжение, тем больше возможная экономия. Конечно, если энергетическая компания поставляет напряжение ближе к 110 В переменного тока, двигатель будет работать более эффективно без каких-либо дополнительных устройств.
Чем выше начальное линейное напряжение, тем больше возможная экономия. Конечно, если энергетическая компания поставляет напряжение ближе к 110 В переменного тока, двигатель будет работать более эффективно без каких-либо дополнительных устройств.
Любой однофазный асинхронный двигатель, практически не работающий, с 25% FLC или менее, является кандидатом на PFC. Тем не менее, он должен работать большое количество часов в год. И чем больше времени он простаивает, как в лесопильном станке, пробивном прессе или конвейере, тем больше вероятность того, что контроллер окупится за несколько лет эксплуатации. Платить за него должно быть втрое легче, чем за более эффективный 3-φ-двигатель. Стоимость PFC не может быть возмещена для двигателя, работающего всего несколько часов в день.
Резюме: Однофазные асинхронные двигатели
- Однофазные асинхронные двигатели не запускаются самостоятельно без вспомогательной обмотки статора, приводимой в действие противофазным током около 90 ° .
 После запуска вспомогательная обмотка не является обязательной.
После запуска вспомогательная обмотка не является обязательной. - Вспомогательная обмотка двигателя с постоянно разделенным конденсатором имеет последовательно включенный конденсатор во время пуска и работы.
- А Асинхронный двигатель с конденсаторным пуском имеет только конденсатор, включенный последовательно с вспомогательной обмоткой во время запуска.
- Двигатель с конденсатором обычно имеет большой неполяризованный электролитический конденсатор, включенный последовательно со вспомогательной обмоткой для запуска, а затем меньший неэлектролитический конденсатор во время работы.
- Вспомогательная обмотка резистивного двигателя с расщепленной фазой создает разность фаз по сравнению с основной обмоткой во время пуска из-за разности сопротивлений.
Механические характеристики трехфазных асинхронных двигателей с однофазным питанием.
УДК 621.313. 33
33
Введение. Асинхронные двигатели (АД) в основном выпускаются с
трехфазные обмотки, питаемые симметричной трехфазной системой
напряжения. Однако на практике может потребоваться переход на однофазный
сети [1], в которых используются конденсаторы, создающие сдвиг фазного тока
в катушке и магнитном поле двигатель становится пульсирующим и вращающимся,
вызывая электромагнитный момент. Также разработаны и широко используются
конденсаторные электродвигатели, которые предназначены для работы от однофазной
сети [5]. И в первом, и во втором случае возникает проблема
расчет их пусковых характеристик и конденсаторов
выбор емкости.
В технической литературе, поскольку метод расчета для различных
номиналы конденсаторов известны [1, 2], но эти методы не
достаточной точностью, поскольку не учитываются должным образом такие факторы, как
как асимметрия мощности магнитного насыщения и тока смещения.
Проблемы анализа режимов работы АД методом математического моделирования
необходимо решить две задачи: выбор математической модели
двигатель и метод расчета. Эти проблемы взаимосвязаны,
Эти проблемы взаимосвязаны,
поскольку использование упрощенной математической модели АД не может адекватно
учитывать факторы, определяющие точность
расчетов, а использование более сложных моделей требует использования
соответствующий математический аппарат.
Цель работы — разработка методики и алгоритма
расчет механических характеристик асинхронных двигателей,
питаются от однофазной сети.
Система уравнений. Трехфазный АД с конденсаторами в одном
фаза по определению перекошена со стороны статора, а значит
для анализа электромагнитных процессов в их наиболее адекватном и
оптимальной системой координат является трехфазная, а не физическая, т. н.
ингибируется [4]. В этой системе контуры статора не
преобразованы, что позволяет адекватно описывать процессы в них, и
трехфазная обмотка ротора заменена равноценной стационарной фазой,
ось которого совпадает с осью обмотки статора.
Система уравнений, описывающая электромагнитные процессы в
АД, трехфазная обмотка статора питается от однофазной сети
показанное на рис. 1, имеет вид [4]
1, имеет вид [4]
[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII] (1)
, где [u.sub.BC] = [квадратный корень из 3][U.sub.m] sin([[omega].sub.0]t
— [pi]/2) – линейное напряжение питания; [U.sub.m], [[omega].sub.0] являются
амплитуда фазного напряжения и угловая частота; [альфа] =
[[омега].sub.0](1 — s)/[квадратный корень из (3)]; s – скольжение;
[[psi].sub.[xi]], [i.sub.[xi]], [r.sub.[xi]] ([xi] = A, B, C, a, b, c)
– потокосцепления, токи и активные опоры цепей;
uk — напряжение на конденсаторе емкостью С.
Методика и алгоритм расчета. Запишем (1) через единицу
векторное уравнение m = 7-го порядка в виде
[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII], (2)
где
[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII].
Система дифференциальных уравнений (2) в форме Коши
выглядит
[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII]. (3)
Поскольку вектор [??](t) = [??](t + T) является периодической функцией
времени в стационарном режиме (при s = const) решение системы
уравнение (3) представляет собой Т-периодические зависимости вектора [??](t) = [??](t +
Т) компоненты. Определение периодических функциональных взаимосвязей
Определение периодических функциональных взаимосвязей
компоненты вектора [??] путем вычисления перехода к
институционализация неприемлема по многим причинам. Такая проблема может
наиболее эффективно решать во вневременной области путем решения границы
задача, разработанная на основе общей теории нелинейных
метод проектирования колебаний, основанный на теоретическом приближении
координаты состояния сплайнов третьего порядка [3]. Формирование границы
задача выполняется на сетке из n узловых точек периода T.
результатом аппроксимации одного дифференциального уравнения системы (3) является
система алгебраических уравнений n-го порядка
[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII], (4)
где H — матрица перехода от непрерывных координат к
их узловые значения, элементы которых определяются только узлами сетки
[3]; [МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII], и для
система дифференциальных уравнений (2) — m векторных уравнений в виде (4)
[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII], (5)
где [МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII];
[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII].
Нелинейная система (5) алгебраических уравнений mn-го порядка представляет собой
дискретное отражение нелинейной системы дифференциальных уравнений (2)
порядка m и i приближается к периоду T. Его решением является вектор
[??] компонентами которого являются значения токов ветвей и напряжения на
конденсатор в сети. С его помощью можно рассчитать не только устойчивые
но также исследовать влияние изменения работы двигателя на любой
должность, которая является частью системы. Для расчета установившегося режима
данный слайд метод продолжения по параметру. Для этой системы
(5) вводим параметр e путем умножения вектора приложенного напряжения
к е и дифференцировать ее на нем. В результате получаем
дифференциальное уравнение (ДУ)
[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII], (6)
где [МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII]
Блочные элементы матрицы Якоби, элементы которых [МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ
ВОСПРОИЗВОДИМО В ASCII] определяются значениями параметров ИМ в
j-й узел.
[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII].
Интегрирующая система ДР (6) по [эпсилон] от [эпсилон] = 0 до
[эпсилон] = 1 находим значения вектора [??] при заданном напряжении,
которое можно уточнить методом Ньютона.
Для изучения влияния на режим работы ИМ любого изменения
координаты, необходимые с учетом неизменного вектора приложенного напряжения, мы
продифференцируем систему (5) по этой координате как параметру. В
частности, при расчете механических характеристик получаем
система ДЭ
[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ, НЕ ВОСПРОИЗВОДИМОЕ В ASCII], (7)
интегрируя которые получаем многомерную характеристику.
Таким образом, матрица Якоби, такая как в (6), и вектор правых частей состоят из n
векторы в виде
[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII],
где [частная производная]B/[частная производная]s равна
матрица B, в которой [альфа] = -[[омега].sub.0]/[квадратный корень из (3)].
Решена задача расчета механических характеристик
в два этапа: на первом рассчитаем установившийся режим при скольжении s =
1. 0, а на втором — зависимости координат как функции
0, а на втором — зависимости координат как функции
проскальзывание от s = 1,0 до заданного значения, а на его основе — механическое
характеристика [M.sub.e] = [M.sub.e](s). Электромагнитный момент
ИМ рассчитывается по формуле [4]
[M.sub.e] = p/[квадратный корень из (3)] [I.sub.[mu]] (([i.sub.[mu]B] —
[i.sub.[mu]C]) [i.sub.A] + ([i.sub.[mu]C] — [i.sub.[mu]A])[i.sub.B] +
([i.sub.[mu]A] — [i.sub.[mu]B])[i.sub.C]).
Для определения матричных элементов [L.sub.j] дифференцированного
индуктивности характеристическая намагниченность основного магнитного пути и
рассеяние в зависимости от рассеяния потока статора (s) и ротора (r)
используются соответствующие токи [4]
[[psi].sub.[mu]] = [[psi].sub.[mu]] ([i.sub.[mu]]),
[[psi].sub.[sigma]s] ([i.sub.s]), [[psi].sub.[sigma]r] =
[[psi].sub.[sigma]r] ([i.sub.r]),
где [i.sub.s], [i.sub.r] — модули векторов, представляющих
эти токи.
Для учета тока смещения в стержнях ротора каждый
из них вместе с короткозамкнутыми кольцами, разделенными по высоте на k
слои. То есть считается, что в роторе имеется k короткозамкнутых
То есть считается, что в роторе имеется k короткозамкнутых
обмотки с соответствующими размерами и каждая заменена на
трехфазный. В этих условиях система уравнений (1)
вместо трех уравнений для ротора мы должны написать 3k уравнений вида
[МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ НЕ ВОСПРОИЗВОДИМО В ASCII].
Увеличение количества уравнений не влияет на расчет
алгоритм и мало влияет на объем вычислений, так как плохо
заполненная матрица Якоби, позволяющая решить систему уравнений с помощью
алгоритм, учитывающий его структуру.
Примеры результатов математического моделирования представлены на рис. 2,
3.
Заключение.
Разработанный метод расчета статических механических свойств
трехфазных АД с короткозамкнутым ротором, которые питаются от однофазной
сети позволяет исследовать влияние конденсаторов
емкость на процесс, чтобы выбрать начало и его значение, которое
обеспечивает необходимый пусковой момент. В основе алгоритма лежит
математическая модель АД, учитывающая магнитное насыщение и
смещение тока в стержнях ротора, а дифференциальный
метод расчета статических характеристик, основанный на решении
краевая задача для системы дифференциальных уравнений электрических
остаток средств.
doi: 10.20998/2074-272X.2016.3.03
ССЫЛКИ
[1.] Беспалов В.Я., Мощинский Ю.А., Петров А.П. Динамика
индикаторы трехфазных асинхронных двигателей, подключенных к однофазным
поставлять. Электротехника—Электротехника, 2000, №1. 1, стр. 13-19.
(Рус).
[2.] Бешта А.С., Семин А.А. Оценка параметров
эквивалентная схема асинхронного двигателя при несимметричном питании
к статору. Электромеханические и энергохозяйства
системы—Электромеханические и энергосберегающие системы, 2014, т. 1, с. 2, с.
10-16. (Рус).
[3.] Маляр В.С., Маляр А.В. Математическое моделирование периодических
режимы электротехнических устройств. Электронное моделирование—Electronic
Моделирование, 2005, вып. 27, нет. 3, стр. 39-53. (Рус).
[4.] Фыльц Р.В. Математические основы теории
Электромеханических преобразователей.
теория электромеханических преобразователей. Киев, издательство «Наукова думка»,
1979. 208 с. (Рус).
[5.] Шуруб Ю.В. Математическая модель асинхронного конденсатора
двигатель с тиристорным управлением. Техническая электродинамика —Техническая
Техническая электродинамика —Техническая
электродинамика, 1999, нет. 4, стр. 52-56. (Рус).
Поступила 09.03.2016
В.С. Маляр (1), д.т.н., профессор,
А.В. Маляр (1), д.т.н., профессор,
(1) Львовский политехнический национальный университет, ул. С. Бандеры, 12,
Львов, 79013, Украина, тел. +380 32 2582119,
e-mail: [email protected]
Надпись: Рис. 1
Подпись: Рис. 2. Периодические зависимости фазных токов
двигатель 4A80B2Y3 при скольжении s = 1,0 и емкости конденсаторов C = 100
[микро]Ф
Подпись: Рис. 3. Статические механические характеристики двигателя
4A80B2Y3 при различных емкостях конденсаторов: C = 100 мкФ (а)
и C = 200 [мкФ] (б)
Индукционные моторные характеристики — Студенческие проекты
Семинары
Проекты
Блоги
Карьера
Наем от US
для бизнеса / университеты
Корпоративная подготовка
Academe Academe Academe Academan
. 0002 Все курсы
0002 Все курсы
Выберите категорию
Загрузка …
Все курсы / Неопределенные
Все курсы / неопределенные / неопределенные
Загрузка …
для предприятий
корпоративные корпорации
для предприятий
.
Академическое обучение
Аренда у нас
Проекты
Мы нанимаем!
ХАРАКТЕРИСТИКИ АИНХРАННОГО ДВИГАТЕЛЯ ЦЕЛЬ – изучить принцип работы и характеристики асинхронного двигателя. Для оценки времени пуска асинхронного привода путем определения характеристик крутящего момента нагрузки и крутящего момента двигателя. Оценить состояние устойчивости асинхронного двигателя с характеристикой момента и скорости. ВВЕДЕНИЕ…
Детали проекта
Загрузка…
Оставить комментарий
Спасибо, что решили оставить комментарий. Пожалуйста, имейте в виду, что все комментарии модерируются в соответствии с нашей политикой комментариев, и ваш адрес электронной почты не будет опубликован по соображениям конфиденциальности. Пожалуйста, оставьте личный и содержательный разговор.
Пожалуйста, оставьте личный и содержательный разговор.
Пожалуйста, войдите, чтобы добавить комментарий
Другие комментарии…
Комментариев пока нет!
Оставьте первый комментарий
Подробнее Проекты Яша Десале (39) . Чтобы проверить производительность конфигурации системы, параметры модели в таких областях, как скорость двигателя, крутящий момент двигателя, состояние заряда, батарея…0476 Подробнее
Проект-1: Моделирование электромобиля с литий-ионным аккумулятором
Цель:
МОДЕЛИРОВАНИЕ ЭЛЕКТРОМОБИЛЯ С ЛИТИЙ-ИОННЫМ АККУМУЛЯТОРОМ Цель – Моделирование электромобиля с использованием асинхронного двигателя и литий-ионного аккумулятора от Powertrain Blockset. Чтобы проверить производительность конфигурации системы, параметры модели в таких областях, как скорость двигателя, крутящий момент двигателя, состояние заряда, батарея…MATLAB
Подробнее
Задача 7-й недели: микроконтроллеры
Цель:
Задача 7-й недели: микроконтроллеры Какая потребность в обмене данными между зарядным устройством, аккумуляторной батареей и электроприводом? Напишите псевдокод для отображения скорости на цифровой приборной панели в соответствии с приведенными ниже условиями; Обновлять отображаемую скорость каждую секунду, включать индикатор высокой эффективности от 50 до 60 км/ч, включать безопасные…
07 фев. 2021 12:13 IST
2021 12:13 IST
Подробнее
Electric Rickshaw Modeling
Цель:
…
30 января 2021 г. 01:04 IST
- MATLAB
Прочтите больше
Week 8. Challenge: Thermal Edagement
. Управление Нарисуйте общую схему системы игрушечной машинки с дистанционным управлением. Каковы различия для реального автомобиля? Каковы требования к охлаждению силового преобразователя? Возьмем пример системы и предположим эффективность и другие параметры. Предложите подходящее решение для поддержания температуры…
18 января 2021 г. 10:03 IST
- MATLAB
Подробнее
Задача 6-й недели: преобразователи мощности силовой преобразователь? Покажите пошаговый процесс для схемы повышающе-понижающего преобразователя. Объясните важность блоков АЦП и ЦАП в замкнутом контуре управления силовым преобразователем. Подготовьте организационную схему людей, работающих в…
Объясните важность блоков АЦП и ЦАП в замкнутом контуре управления силовым преобразователем. Подготовьте организационную схему людей, работающих в…
11 января 2021 г. 13:10 IST
- MATLAB
Подробнее
Задача 5-й недели: Аналоговые системы управления
Цель:
Задача 5-й недели: Аналоговые системы управления Сравните аналоговую систему управления с цифровой применительно к двигателю электромобиля. Расскажите о событиях, связанных с обратным звонком и обновлением по беспроводной сети автомобильными компаниями. Использование диаграммы тела графика MATLAB для выбранной передаточной функции в s-области и…MATLAB
Подробнее
Задача 4-й недели: ПИД-регуляторы
Цель:
Задача 4-й недели: ПИД-регуляторы В каких ситуациях упреждающее управление двигателем постоянного тока не работает? Подготовьте сценарий MATLAB для управления с прямой связью и протестируйте его. Предположим, есть установка и контроллер. Используя блок ПИД-регулятора MATLAB, проверьте реакцию системы с помощью Общего наблюдения за усилением ПИД-регулятора. Рассмотрим систему ниже …
Предположим, есть установка и контроллер. Используя блок ПИД-регулятора MATLAB, проверьте реакцию системы с помощью Общего наблюдения за усилением ПИД-регулятора. Рассмотрим систему ниже …
29 декабря 2020 г. 14:08 IST
- MATLAB
92 + 14s + 40.02) Время нарастания менее 0,5 секунды, установившаяся ошибка менее 5 %, перерегулирование менее 10 %, коэффициент усиления больше…
25 декабря 2020 г.
Подробнее
Задача 2-й недели: графики Боде и ступенчатая характеристика
Цель:
Задача 2-й недели: диаграммы Боде и ступенчатая характеристика Цель – какие команды MATLAB связаны с передаточной функцией, полюсно-нулевым усилением и ступенчатой характеристикой ? Возьмите пример передаточной функции и примените все команды. Для единой системы обратной связи, показанной на рисунке ниже. Определите переходную характеристику с замкнутым контуром, используя команды MATLAB. …
…
18 декабря 2020 года 2:43 вечера IST
- MATLAB
Подробнее
Неделя 1 — Трансферная функция
Цель:
неделя 1 — Переводя системы? Получите передаточную функцию автомобиля и преобразуйте ее в формат пространства состояний. Одинаковы ли передаточные функции цепей RC и CR (выход через R)? Как эксплуатируются гибридные электромобили дальше…
08 Dec 2020 13:57 IST
Подробнее
Заключительный проект: Дизайн электромобиля
Цель:
ПРОЕКТ 2 – КОНСТРУКЦИЯ ЭЛЕКТРОТРАНСПОРТНОГО СРЕДСТВА ЦЕЛЬ – Создать в MATLAB модель электромобиля, использующего литий-ионный аккумулятор и асинхронный двигатель. Выберите подходящие блоки из Powertrain Blockset. ВВЕДЕНИЕ. Электромобиль определяется как транспортное средство, в котором для приведения в движение используется электродвигатель или тяговый двигатель, как…0232
Подробнее
Проект-1: Силовой агрегат для самолетов на взлетно-посадочных полосах
Задача:
ПРОЕКТ 1 – СИЛОВОЙ ПРИВОД ДЛЯ САМОЛЕТОВ НА ВПП Цель – Найти и перечислить общий вес различных типов самолетов. Есть ли разница между скоростью по земле и скоростью по воздуху? Почему не рекомендуется использовать мощность двигателя самолета для его перемещения по земле в аэропорту? Как самолет выталкивают на взлетно-посадочную полосу…
Есть ли разница между скоростью по земле и скоростью по воздуху? Почему не рекомендуется использовать мощность двигателя самолета для его перемещения по земле в аэропорту? Как самолет выталкивают на взлетно-посадочную полосу…
22 ноября 2020 г. 13:10 IST
Подробнее
неделя-11 Задача: торможение
Цель:
неделя 11 Задача-Цель торможения-для расчета энергии, необходимой для торможения для определенного цикла привода. Чтобы понять, почему электродвигатели не могут развивать тормозной момент на более высокой скорости, как при запуске, а также сравнить механические…
14 ноября 2020 г. 13:36 IST
Подробнее
Неделя 11 Задача — ТОРМОЖЕНИЕ
Цель:
…
14 ноября 2020 г., 13:32 IST
- MATLAB
Прочитайте больше
рабочего цикла и сигнал контроля, созданный для конвертации мощности усиления.
Цель:
РАБОЧИЙ ЦИКЛ И СИГНАЛ УПРАВЛЕНИЯ, СОЗДАВАЕМЫЙ ДЛЯ ЦЕПИ ПРЕОБРАЗОВАТЕЛЯ ПОВЫШАЮЩЕЙ МОЩНОСТИ. ПОЧЕМУ СИЛОВЫЕ ЭЛЕКТРОННЫЕ СХЕМЫ ЭФФЕКТИВНЫ? КАКИЕ ВИДЫ ПОТЕРЬ ПРОИСХОДЯТ В СИЛОВЫХ ЭЛЕКТРОННЫХ ЦЕПЯХ НА ПРАКТИКЕ? Силовая электроника — это применение твердотельной электроники для управления и преобразования электроэнергии. Первый…
06 ноября 2020 г. 03:32 AM IST
- MATLAB
- Power Converter
Чтение. Модель двигателя MATLAB. 3 фазы 50 Гц. Асинхронный двигатель, представленный константами эквивалентной схемы X1 = X2 = 0,1 Ом. & R1 = R2 = 0,2 Ом. Работает наполовину при номинальном напряжении и частоте. Рассчитать коэффициент запуска…
25 октября 2020 г. 06:24 AM IST
- MATLAB
ЧИТАТЬ ДОПОЛНЕНИЕ
Индукционный моторный Для оценки времени пуска асинхронного привода путем определения характеристик крутящего момента нагрузки и крутящего момента двигателя. Оценить состояние устойчивости асинхронного двигателя с характеристикой момента и скорости. ВВЕДЕНИЕ…
Оценить состояние устойчивости асинхронного двигателя с характеристикой момента и скорости. ВВЕДЕНИЕ…
19 окт. 2020 г. 10:53 IST
Подробнее
Управление двигателем постоянного тока
Цель:
не поднимается, когда двигатель меняет направление с прямого на обратное. См. раздел справки «Four Quadrant Chopper DC Drive (DC7) Block», сравните его…
12 окт.0917 ТРАНСМИССИЯ EV
Цель:
ТРАНСМИССИЯ EV ЦЕЛЬ – Понять различные типы преобразователей энергии, используемые в EV и HEV. Коэффициент заполнения и силовая электроника по управлению транспортным средством. Взгляд автора на асинхронные и бесколлекторные двигатели постоянного тока Уолли Риппеля, Тесла. Q.1) Какие типы цепей преобразователя мощности используются в электрических…
Цель:
…
27 сентября 2020 г. 11:08 AM IST
11:08 AM IST
- HEV
- MATLAB
Читать Подробнее
Широкие открытые дроссельные. BLOCKSETS AIM –…
20 сентября 2020 г. 11:57 IST
- HEV
- MATLAB
Читать подробности
Инструмент консультанта
Цель:
Имя проекта — Advisor Tool Aive — использовать инструмент консультанта для моделирования. Цель — используйте ev_defaults_in_file,…
15 сентября 2020 11:25 AM IST
- MATLAB
Читать Подробнее
Широко открытое условие дросселя (WOT) Условие
Объектив:
. ) СОСТОЯНИЕ…
06 сентября 2020 2020 года 2:43 IST
- MATLAB
Читать подробности
Неделя — 4
Цель:
Название проекта — Логика управления стиральной машиной и механизмом передачи. стиральная машина с использованием Stateflow, задавая определенные условия в соответствии с потребляемой мощностью и потреблением воды. В соответствии с этим входом машина работает и получает результат при свете лампы. Создать…
стиральная машина с использованием Stateflow, задавая определенные условия в соответствии с потребляемой мощностью и потреблением воды. В соответствии с этим входом машина работает и получает результат при свете лампы. Создать…
30 авг. 2020 13:13 IST
Подробнее
Логика управления стиральной машиной и механизмом переключения передач с использованием StateFlow
Цель:
Имя проекта -логика управления стиральной машиной и механизмом сдвига передач с использованием Astalflow AIM -реализация логики управления стиральной машиной с использованием StateFlow, давая определенные условия. в соответствии с потребляемой мощностью и потреблением воды.…
30 августа 2020 г. 13:08 IST
- MATLAB
Читать далее
ПРОЕКТ 3 – МАССОВЫЙ ПРУЖИННЫЙ ДЕМПФЕР В SIMSCAPE И SIMUPLINMP МОДЕЛИ И РАСЧЕТА G ДАННОЕ УРАВНЕНИЕ В МОДЕЛИ SIMULINK.
Цель:
Project 3 — Массовая пружина в модели SIMSCAPE и SIMULINK и вычисление рабочего времени для заданного ввода и применения данного уравнения…
22 августа 2020 11:03 AM IST
- MATLAB
Read
2
2
2
2
2
2
2
9029
. МОДЕЛЬ SIMULINK ДЛЯ ДВЕРНОГО ЗВОНКА И ТЕРМИСТОРА
Цель:
НАЗВАНИЕ ПРОЕКТА – МОДЕЛЬ SIMULINK ДЛЯ ДВЕРНОГО ЗВОНКА И ТЕРМИСТОРА Цель: создать модель Simulink для дверного звонка с использованием соленоидного блока. Использовать термистор для измерения температуры нагревателя и включения/выключения вентилятора. ДВЕРНОЙ ЗВОНОК- Объяснение модели Simulink – Мы использовали следующие блоки…
19 августа 2020 г. 10:49 AM IST
Читать дальше
неделя 1 Задача — (Основы Simulink)
Цель:
…
11 августа 2020 11:13 AM IST
- MATLAB
- MATLAB
9
- MATLAB
9
- MATLAB
- MATLAB
НАЗВАНИЕ ПРОЕКТА — СИЛЫ, ДЕЙСТВУЮЩИЕ НА ТРАНСПОРТНОЕ СРЕДСТВО
Задача:
В.
 1 – Какой должна быть максимальная скорость двигателя, используемого в электрическом самокате, способном развивать скорость 90 км/ч, если фиксированное передаточное число равно 7, а размер шин 90/100 R10 53J? Также пересчитать значение, если код 90/90/R18 53P? Пример -…
1 – Какой должна быть максимальная скорость двигателя, используемого в электрическом самокате, способном развивать скорость 90 км/ч, если фиксированное передаточное число равно 7, а размер шин 90/100 R10 53J? Также пересчитать значение, если код 90/90/R18 53P? Пример -…03 августа 2020 года, 2:33 вечера IST
Подробнее
Проект 2 — Симулятор цикла Ранкина
Цель:
Проект…
15 июля 2020 г. 20:15 IST
Подробнее
Проект 1. Анализ термодинамических данных НАСА
Цель:
НАЗВАНИЕ ПРОЕКТА – РАЗБОР ТЕРМОДИНАМИЧЕСКИХ ДАННЫХ НАСА ЦЕЛЬ- Написать программу MATLAB для извлечения коэффициентов из MATLAB extras\THERMO.dat.txt для расчета энтальпии, энтропии, удельной теплоемкости для всех веществ в файле данных.
 Кроме того, построив графики каждого вида и найдя молекулярную массу…
Кроме того, построив графики каждого вида и найдя молекулярную массу…09 Jul 2020 18:45 IST
Подробнее
Неделя 4 — Генетический алгоритм
Цель:
НАЗВАНИЕ ПРОЕКТА — ГЕНЕТИЧЕСКИЙ АЛГОРИТМ В этом проекте мы решим задачу глобальной оптимизации. Мы использовали MATLAB для написания определенных программ, и в этом процессе мы научились использовать циклы for, условия if, а также функции. Итак, что такое оптимизация? Когда дело доходит до нашей инженерной функции, это может быть что-то…
29 июня 2020 г. 18:50 IST
Подробнее
ВЫПОЛНЕНИЕ ПОДБОРКИ КРИВЫХ С ИСПОЛЬЗОВАНИЕМ MATLAB
Цель:
Название проекта -…
23 июня 2020 г. 05:35 IST
- MATLAB
Прочтите больше
Решение ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ИСПОЛЬЗОВАНИЕМ MATLAB Дифференциал 2-го порядка…
18 июня 2020 года, 2:47 вечера IST
- MATLAB
Читать подробности
Цикл воздушного стандарта (цикл OTTO) с использованием MATLAB
Объектива:
Название проекта — Air Standard…
12 Jun 2020 08:48888888.
 IST
IST- MATLAB
Читать Подробнее
Кинематика вперед 2R Robotic Arm
Цель:
Проект…
11 июня 2020 г. 06:59 AM IST
- MATLAB
Подробнее
Поток через велосипед
Объектив:
Название проекта — поток над бициклером — чтобы найти связь между сопротивлением и velocity. учитывая площадь велосипедиста и изменение скорости езды на велосипеде по отношению к входящей скорости. напишите программу для построения графика зависимости коэффициента сопротивления от силы сопротивления и выясните взаимосвязь между…
08 июня 2020 г. 18:18 IST
- MATLAB
Подробнее
Основы MATLAB
Цель:
НАЗВАНИЕ ПРОЕКТА – ОСНОВЫ MATLAB ЦЕЛЬ: — Узнать результаты, выполняя различные команды MATLAB и знакомясь с синтаксисом MATLAB.
 ЦЕЛИ: — Построить прочную основу синтаксиса MATLAB. Понимание графического интерфейса MATLAB. Понимать основные функции и команды в MATLAB. Чтобы понять…
ЦЕЛИ: — Построить прочную основу синтаксиса MATLAB. Понимание графического интерфейса MATLAB. Понимать основные функции и команды в MATLAB. Чтобы понять…08 июня 2020 г. 18:13 IST
- MATLAB
Узнать больше
Показаны 1 из 39 проектов
Попробуйте наши лучшие инженерные курсы, проекты и семинары уже сегодня! Закажите БЕСПЛАТНУЮ демонстрацию
Механические и электрические характеристики асинхронных двигателей
В этой статье будет освещена тема механических и электрических характеристик электродвигателей. На примере асинхронного двигателя рассмотрим такие параметры, как мощность, работа, КПД, косинус фи, крутящий момент, угловая скорость, линейная скорость и частота. Все эти характеристики важны при проектировании оборудования, в котором электродвигатели выполняют роль приводных двигателей. Особое распространение в промышленности сегодня получили асинхронные электродвигатели, поэтому остановимся на их характеристиках.
 Например, рассмотрим AIR80V2U3.
Например, рассмотрим AIR80V2U3.Номинальная механическая мощность асинхронного двигателя
На заводской табличке (на заводской табличке) двигателя всегда указывается номинальная механическая мощность на валу двигателя. Это не та электроэнергия, которую этот электродвигатель потребляет из сети.
Так, например, для двигателя АИР80В2У3 номинальная мощность 2200 Вт соответствует именно механической мощности на валу. То есть в оптимальном режиме работы этот двигатель способен каждую секунду совершать механическую работу в 2200 Дж. Обозначим эту мощность как P1 = 2200 Вт.
Номинальная активная электрическая мощность асинхронного двигателя
Для определения номинальной активной электрической мощности асинхронного двигателя по данным паспортной таблички необходимо учитывать КПД. Итак, для этого электродвигателя КПД составляет 83%.
Что это значит? Это означает, что только часть активной мощности, поступающей из сети в обмотки статора двигателя и безвозвратно потребляемой двигателем, преобразуется в механическую мощность на валу.
 Активная мощность P = P1/КПД. Для нашего примера по представленному шильдику видим, что Р1=2200, КПД=83%. Итак, P = 2200/0,83 = 2650 Вт.
Активная мощность P = P1/КПД. Для нашего примера по представленному шильдику видим, что Р1=2200, КПД=83%. Итак, P = 2200/0,83 = 2650 Вт.
Номинальная полная электрическая мощность асинхронного двигателя
Суммарная электрическая мощность, подводимая к статору электродвигателя от сети, всегда больше механической мощности на валу и больше активной мощности, безвозвратно потребляемой электродвигатель.
Чтобы найти полную мощность, достаточно разделить активную мощность на косинус фи. Таким образом, полная мощность равна S = P/Cosφ. Для нашего примера P = 2650 Вт, Cosφ = 0,87. Следовательно, общая мощность S = 2650/0,87 = 3046 ВА.
Номинальная реактивная электрическая мощность асинхронного двигателя
Часть общей мощности, подводимой к обмоткам статора асинхронного двигателя, возвращается в сеть. it реактивная мощность Q.
Q = √(S 2 — P 2 )
Реактивная мощность связана с полной мощностью через sinφ и связана с активной и полной мощностью через квадратный корень.
 Для нашего примера:
Для нашего примера:Q = √(3046 2 — 2650 2 ) = 1502 ВАР
Реактивная мощность Q измеряется в ВАр — в реактивных вольт-амперах.
Теперь посмотрим на механические характеристики нашего асинхронного двигателя: номинальный рабочий момент на валу, угловая скорость, линейная скорость, скорость вращения ротора и ее связь с частотой электродвигателя.
Частота вращения асинхронного двигателя
На шильдике видно, что при питании переменным током 50 Гц ротор двигателя работает при номинальной нагрузке 2870 об/мин, эту частоту обозначим n1.
Что это значит? Так как магнитное поле в обмотках статора создается переменным током частотой 50 Гц, то для двигателя с одной парой полюсов (а это АИР80В2У3) частота «вращения» магнитного поля, синхронная частота n , равна 3000 об/мин, что идентично 50 об/мин. Но поскольку двигатель асинхронный, ротор вращается позади на величину скольжения s.
Значение s можно определить, разделив разницу между синхронной и асинхронной частотами на синхронную частоту и выразив это значение в процентах:
s = ((n – n1)/n)*100%
Для нашего примера s = ((3000 – 2870)/3000)*100% = 4,3%.

Угловая скорость асинхронного двигателя
Угловая скорость ω выражается в радианах в секунду. Для определения угловой скорости достаточно скорость вращения ротора n1 перевести в обороты в секунду (f), и умножить на 2 Пи, так как один полный оборот равен 2 Пи или 2*3,14159 радиан. Для двигателя АИР80В2У3 асинхронная частота n1 равна 2870 об/мин, что соответствует 2870/60 = 47,833 об/мин.
Умножая на 2 Пи, имеем: 47,833 * 2 * 3,14159 = 300,543 рад/с. Можно перевести в градусы, для этого вместо 2 Пи подставить 360 градусов, тогда для нашего примера получим 360*47,833=17220 градусов в секунду. Однако такие расчеты обычно ведутся именно в радианах в секунду. Следовательно, угловая скорость ω = 2 * Pi * f, где f = n1 / 60.
Линейная скорость асинхронного двигателя
Линейная скорость v относится к оборудованию, на котором асинхронный двигатель установлен в качестве привода .
 Так, если на вал двигателя установить шкив или, скажем, наждачный диск известного радиуса R, то линейную скорость точки на ребре шкива или диска можно найти по формуле:
Так, если на вал двигателя установить шкив или, скажем, наждачный диск известного радиуса R, то линейную скорость точки на ребре шкива или диска можно найти по формуле:v = ωR
Номинальный крутящий момент асинхронного двигателя
Каждый асинхронный двигатель характеризуется номинальным крутящим моментом Mn. Крутящий момент M связан с механической мощностью P1 через угловую скорость следующим образом:
P = ωM
Крутящий момент или момент силы, действующий на определенном расстоянии от центра вращения, сохраняется для двигателя, а с увеличением радиуса , сила уменьшается, и чем меньше радиус, тем больше сила, потому что:
M = FR
Итак, чем больше радиус шкива, тем меньшая сила действует на его край, а наибольшая сила действует непосредственно на вал электродвигателя.
Например, для двигателя АИР80В2У3 мощность P1 равна 2200 Вт, а частота n1 равна 2870 об/мин или f = 47,833 об/мин. Следовательно, угловая скорость равна 2*Pi*f, т.
 е. 300,543 рад/с, а номинальный крутящий момент Mn равен P1/(2*Pi*f). Мн = 2200/(2*3,14159*47,833) = 7,32 Н*м.
е. 300,543 рад/с, а номинальный крутящий момент Mn равен P1/(2*Pi*f). Мн = 2200/(2*3,14159*47,833) = 7,32 Н*м.Таким образом, исходя из данных, указанных на шильдике асинхронного двигателя, можно узнать все основные электрические и механические параметры.
Надеемся, что эта статья помогла вам понять, как связаны угловая скорость, частота, крутящий момент, активная, полезная и полная мощность, а также КПД электродвигателя.
Анализ механических характеристик трехфазного асинхронного двигателя
Заголовки статей
Исследование методов управления очисткой сточных вод на основе Интернета вещей
стр. 611Динамическое координированное управление переключением передач для гибридного электромобиля
стр. 615
615Проектирование адаптивных систем круиз-контроля на основе квадратичной теории ограниченности
стр. 619Анализ неисправности шестеренчатого насоса с внешним зацеплением
стр. 623Анализ механических характеристик трехфазного асинхронного двигателя
стр. 627Исследование технологии разрушения излома шатуна на базе автомобильного двигателя TSI
стр. 631Анализ человеческого фактора двери автомобиля виртуальной сборки на основе виртуальной среды CATIA
стр. 635
635Анализ и оптимизация конструкции шасси миниатюрного электрического туристического автомобиля
стр. 639Отслеживание траектории недостаточно активированного манипулятора с использованием нечеткого метода
стр. 643Главная Advanced Materials Research Advanced Materials Research Vols. 791-793 Анализ механических характеристик…
Предварительный просмотр статьи
Резюме:
Проанализирована функциональная связь между электромагнитным моментом трехфазного асинхронного двигателя и некоторыми факторами; построена кривая механической характеристики работы двигателя; Присущие механические свойства и механические свойства человека исследуются в конкретном приложении. Факты доказывают, что анализ механических характеристик трехфазных асинхронных двигателей важен для снижения частоты отказов трехфазного асинхронного двигателя, повышения производительности и эффективности производства.

Доступ через ваше учреждение
использованная литература
[1]
Вэнь Хуйся. обсуждение механических характеристик трехфазных асинхронных двигателей, пуска, торможения и скорости [J], Вестник инноваций в области науки и техники, 2011 (27) 71~74.[2]
Чен Джи. Фотоэлектрическое преобразование в PN-переходе высокочистого кремния P-типа [J]. Полупроводниковая электроника, 2008: 19(3): 208~209.
Полупроводниковая электроника, 2008: 19(3): 208~209.[3]
Ли Хуабинь. механические характеристики трехфазных асинхронных двигателей, теория торможения [J]. научно-техническая информация, 2011 (19): 524.[4]
Ян Хоучуань, Ван Дунфэн, Чанчунь. механические свойства сетевой виртуальный эксперимент разработки трехфазного асинхронного двигателя [J]. Разработка и инновации в области механических и электрических изделий, 2006 г. (4): 77–97.[5]
Цзе Цзиньчжу, Ван Ванью. диагностика неисправностей и техническое обслуживание механического и электрического оборудования [M]. Пекин: пресса химической промышленности. (2010).
диагностика неисправностей и техническое обслуживание механического и электрического оборудования [M]. Пекин: пресса химической промышленности. (2010).[6]
Лю Цзилинь. двигатели и электрическое управление [M]. Пекин: Издательство электронной промышленности. (2008).Цитируется
Электрические машины — кривая скорости крутящего момента асинхронного двигателя
Крутящий момент асинхронного двигателя
Уравнения крутящего момента
Как и во всех вращающихся механических системах в установившемся режиме, крутящий момент можно найти по мощности и механической скорости
\[
\tau=\frac{P}{\omega}
\]В случае асинхронной машины электромагнитный момент, создаваемый машиной, до вычета механических (или вращательных) потерь определяется как
\[
\tau = \frac{P_{conv}}{\omega_m}
\]Используя определения мощности, преобразованной через мощность воздушного зазора и механическую скорость как функцию синхронной скорости:
\[
\begin{выровнено}
\tau & = \frac{(1-s)P_{gap}}{(1-s)\omega_s} \\
\tau & = \frac{P_{пробел}}{\omega_s}
\end{выровнено}
\] 92R_2}{с\омега_с}
\]не дает простого понимания того, как крутящий момент машины зависит от скорости, поскольку ток ротора является функцией скольжения.
 Чтобы построить кривую скорости вращения,
Чтобы построить кривую скорости вращения,
нам нужно сначала решить модель схемы, чтобы найти ток ротора. В отсутствие
компьютера, это в лучшем случае утомительный процесс. Множественные решения приведенного выше уравнения для крутящего момента при различных
проскальзывания можно упростить, упростив модель эквивалентной схемы. Рассмотрим пофазную эквивалентную схему на рис. 1:Рис. 1. Схема замещения асинхронного двигателя по фазам
Статорную часть схемы замещения (вместе с намагничивающей ветвью) можно заменить на
эквивалентная схема Тевенина. В схеме Thevenin фазное напряжение статора было заменено его эквивалентом Thevenin,\[
\begin{выровнено}
\vec{V}_{TH} & =\frac{jX_m}{R_1+j\left(X_1+X_m\right)}\vec{V}_1 \\
V_{TH} & = |\vec{V}_{TH}|
\end{выровнено}
\]и импедансы были заменены эквивалентными импедансами Thevenin.
\[
\begin{выровнено}
Z_{TH} & =\left(R_{1}+jX_1\right)|| jX_m \\
Z_{TH} & = \frac{jX_m\left(R_1+jX_1\right)}{R_1+jX_1+jX_m} \\
Z_{TH} & = R_{TH}+jX_{TH}
\end{выровнено}
\]Рис.
 2. Пофазный асинхронный двигатель в эквивалентной схеме модели
2. Пофазный асинхронный двигатель в эквивалентной схеме моделиИспользование схемы на рис. 2 значительно упрощает расчет тока ротора
\[
\begin{выровнено}
\vec{I}_2 & =\frac{\vec{V}_{TH}}{Z_{TH}+Z_2} \\
\vec{I}_2 & =\frac{\vec{V}_{TH}}{\left(R_{TH}+\frac{R_2}{s}\right)+j\left(X_{TH} +X_2\справа)}
\end{выровнено}
\] 92 } \frac{R_2} {s\omega_s}
\end{выровнено}
\]Используя приведенное выше уравнение, можно напрямую построить график зависимости крутящего момента от проскальзывания.
Кривая скорости вращения
Общая кривая
Используя уравнение крутящего момента Тевенина, относительно легко вычислить крутящий момент как функцию проскальзывания. Это показано на рис. 3 в диапазоне проскальзывания от +1 до -1. Помня, что \(\omega_m=(1-s)\omega_s\), скольжение +1 соответствует скорости \(\omega_m=-\omega_s\) или \(n_m=-n_s\), а скольжение -1 соответствует скорости \(\omega_m=2\omega_s\), \(n_m=2n_s\).
Рис. 3. Момент асинхронного двигателя — кривая скорости
Рабочие области
Кривая крутящий момент-скорость делится на три рабочие области:
- Торможение, \(n_m \lt 0\), \(s \gt 1\)
Крутящий момент положителен, а скорость отрицательна. Учитывая уравнение преобразования мощности
Учитывая уравнение преобразования мощности\[
P_{conv}=(1-s)P_{пробел}
\]можно видеть, что если преобразованная мощность отрицательна (от \(P=\tau \omega\))
тогда мощность воздушного зазора положительна. то есть мощность течет от статора к ротору, а также в ротор от
механическая система. Эта операция также называется затыканием.
Этот режим работы можно использовать для быстрой остановки машины. Если двигатель движется вперед, его можно остановить
поменяв местами подключения к двум из трех фаз. Переключение двух фаз приводит к изменению
направление движения магнитного поля статора, эффективно переводя машину в режим торможения в противоположном направлении. - Движение, \( 0 \lt n_m \lt n_s \), \( 0 \lt s \lt 1 \)
Крутящий момент и движение в одном направлении. Это самый распространенный режим работы. - Генерация,\(n_m \gt n_s\), \(s \lt 0\)
В этом режиме снова крутящий момент положительный, а скорость отрицательная. Однако, в отличие от затыкания,\[
P_{conv}=(1-s)P_{пробел}
\]указывает, что если преобразованная мощность отрицательна, мощность воздушного зазора тоже.
 В этом случае энергия поступает от механического
В этом случае энергия поступает от механического
системы, в цепь ротора, затем через воздушный зазор в цепь статора и внешнюю электрическую систему.
Характеристика крутящего момента двигателя
Наибольший интерес представляет двигательная область кривой крутящий момент-скорость асинхронной машины.
На приведенных ниже графиках показано несколько различных кривых крутящего момента и скорости из-за различий в конструкции двигателей. Общие черты
интерес отмечены и обсуждаются ниже.Рис. 4. Графики крутящего момента и скорости в автомобильной области
- \(\tau_{rated}\). Номинальный крутящий момент машины. Это проектная рабочая точка.
- \(\тау_{начало}\). Начальный крутящий момент машины, когда машина находится в состоянии покоя. 92R\) потери будут чрезмерными.)
- \(\тау_{пу}\). Тяговый момент машины. В некоторых машинах самая низкая точка по крутящему моменту скорости
кривая между пуском и вытягиванием не является пусковым крутящим моментом. В этом случае важно знать тяговый момент. Это минимальный крутящий момент
В этом случае важно знать тяговый момент. Это минимальный крутящий момент
что двигатель может разогнаться до желаемой рабочей скорости.
В установившемся режиме работы асинхронный двигатель будет работать на скорости, при которой момент механической нагрузки равен
крутящий момент, развиваемый двигателем. На низких скоростях разница между крутящим моментом двигателя и крутящим моментом нагрузки ускоряет машину.
Нормальная работа находится справа от максимального крутящего момента \(\left(s\lt s_{po}\right)\). В этой области увеличение крутящего момента нагрузки приведет к замедлению двигателя, увеличивая крутящий момент двигателя до тех пор, пока не будет достигнуто равновесие. Слева от момента отрыва такое равновесие не может быть достигнуто. Механически,\[
\tau_{двигатель}-\tau_{нагрузка}=J\frac{d\omega_m}{dt}
\]где \(J\) — инерция вращения механической системы.
Момент вытягивания
Уравнение крутящего момента Тевенина использовалось выше для построения кривой крутящий момент-скорость асинхронной машины.