Тепловой КПД теплового двигателя: что, формула, как найти

В этой статье обсуждается тепловой КПД тепловой машины. Разобьем тему на две части. Сначала мы изучим тепловую машину, затем тепловую эффективность и, наконец, тепловую эффективность тепловой машины.

Мы не можем представить свою жизнь без тепловой машины. Тепловые двигатели уже давно являются частью нашей жизни, и они сделали нашу жизнь намного проще. В этой статье мы подробно изучим тепловые двигатели и обсудим их эффективность. Мы также обсудим различные типы тепловых двигателей.

Что такое тепловая машина?

Тепловой двигатель — это механическое устройство, использующее принципы термодинамики для преобразования тепловой энергии в механическую.

Тепловая энергия поступает от рабочего тела, которым может быть вода, пар или любая другая жидкость. Тепловая энергия будет преобразована в механическую энергию после входа в турбину. Преобразованная механическая энергия может использоваться во многих приложениях, таких как приведение в движение локомотивов и даже для производства электроэнергии.

Что является рабочим органом тепловой машины?

Тепловая машина представляет собой сборку из четырех основных частей, которые работают вместе, производя работу. Эти части приведены в списке ниже-

• Котел- котел добавит тепла к рабочему жидкость. Для паровой машины это тепло превращает жидкую воду в пар. Этот пар имеет высокое давление и самую высокую энтальпию. Этот пар передается на турбину на следующей ступени.
• турбина– Турбина является основным узлом тепловой машины. Работа производится в турбине, поскольку она преобразует тепловую энергию в механическую энергию. Давление пара при этом снижается. Однако фаза не меняется.
• Конденсатор– Конденсатор преобразует пар низкого давления в жидкость низкого давления. Это означает, что газообразная фаза превращается в жидкую фазу. Температура рабочего тела не меняется, поэтому можно сказать, что весь процесс фазового перехода является изотермическим процессом.
• Компрессор– Компрессор увеличивает давление жидкости и нагнетает ее в котел. Таким образом, рабочая жидкость после прохождения через компрессор становится жидкостью под высоким давлением.

Примеры циклов теплового двигателя-

Внутри тепловой машины используемое рабочее тело может быть разным. Даже компоненты могут различаться в зависимости от типа приложения. Разные типы и, следовательно, наиболее часто используемые тепловые двигатели циклы обсуждаются в разделе, данном ниже-

1. Газовые циклы– Газовые циклы имеют рабочее тело в газообразной форме. Наиболее часто используемой рабочей жидкостью является пар. Фаза рабочего тела не меняется в газовых циклах. Различные типы газовых циклов: цикл Карно, цикл Брайтона, цикл Стирлинга и т. Д.
2. Жидкостные циклы– Как следует из самого названия, жидкостные циклы используют только жидкость в качестве рабочего тела. Фаза рабочего тела не меняется. Примерами жидкостных циклов являются цикл Стерлинга и рекуперативный двигатель.
3. Электронные циклы– Электронные циклы используются в различных областях: термогальванический элемент, термотуннельное охлаждение и термоэлектронная эмиссия.
4. Магнитные циклы. Термомагнитный двигатель использует магнитный цикл.

Что такое тепловой КПД?

Термический КПД — это просто отношение произведенной работы к теплу, переданному двигателю.

Тепловой КПД говорит нам о том, насколько эффективен тепловой двигатель. Чтобы измерить количество работы, производимой при заданном количестве подводимой теплоты, мы вычисляем тепловую эффективность. Полезную работу производит турбина п тепловые машины. Математически тепловой КПД определяется как:

Тепловой КПД = (чистая выполненная работа / подводимая теплота)

Изображение: Совершенная работа всегда меньше подводимой теплоты.

Кредиты изображения: Википедия

Что такое тепловой КПД тепловой машины

Мы уже обсуждали тепловую эффективность в предыдущем разделе. Тепловая энергия тепловой машины есть отношение двух величин.

Первая величина представляет собой чистую работу, выполняемую турбиной, а вторая величина представляет собой тепло, добавляемое через котел. Турбина выполняет некоторую работу, из которой часть работы используется для работы компрессора. Оставшаяся работа называется чистой работой, производимой турбиной. Теплота, подводимая котлом к ​​рабочему телу, называется подводом тепла в систему или тепловой машиной.

Тепловой КПД формулы тепловой машины

Мы достаточно обсудили формулу, относящуюся к тепловому КПД тепловой машины.

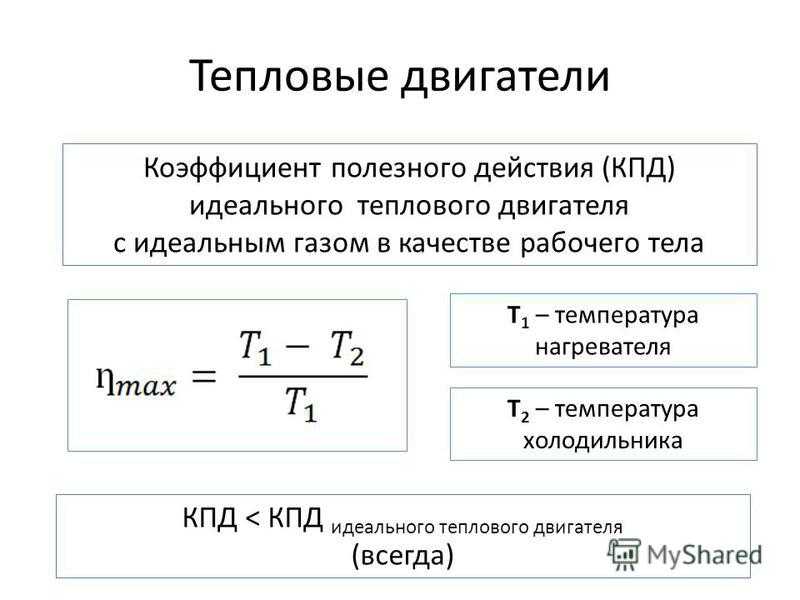
Тепловой КПД тепловой машины находится по следующей формуле:

Где eta означает тепловой КПД

Wnet – чистая работа, производимая турбиной.

Q1 – теплота, подводимая котлом к ​​тепловой машине.

Как найти КПД тепловой машины?

Мы уже обсуждали это в предыдущих разделах. Эффективность или тепловой КПД тепла двигатель определяется как отношение работы отдачу к подводимой теплу в системе.  

Чтобы найти чистую работу, производимую двигателем, вычитаем работу, совершаемую турбиной, и работу, передаваемую компрессору для его работы. Оставшееся количество – чистая проделанная работа.

Как найти произведенную чистую работу?

Нет необходимости, чтобы произведенная чистая работа была равна полной работе, произведенной турбиной. Это связано с тем, что некоторая часть работы передается компрессору для его работы.

Турбина является основным компонентом тепловой машины, которая производит работу. Компрессор — это устройство, поглощающее работу, которое работает после поглощения некоторой работы, производимой турбиной. Разница между полной работой, произведенной турбиной, и работой, переданной компрессору, называется чистой работой, выполненной в системе, или чистой работой, произведенной в системе.

Математически,

Проделанная работа = Работа, выполненная турбиной – Работа, поглощенная компрессором.

Принцип работы тепловой машины

Тепловые двигатели работают по простому принципу: берут тепло из резервуара тепла, называемого источником тепла, производят из него некоторую работу и направляют оставшееся тепло в другой резервуар тепла, называемый теплоотводом.

Энергия, которая передается в тепловом двигателе, подчиняется закону сохранения. В этом процессе не создается и не уничтожается лишнее тепло. Тепловая машина не сможет преобразовать все тепло работать. Какая-то сумма всегда уходит в раковину. Здесь вступает в действие коэффициент полезного действия, который показывает, какую работу двигатель может произвести с заданным количеством подводимого тепла.

Второй закон термодинамики для тепловой машины

Есть некоторые законы термодинамики, которым следует любая тепловая машина. Второй закон термодинамики для тепловой машины приведен ниже:

Второй закон термодинамики Тепловая машина не может извлекать теплоту из источника тепла и полностью превращать ее в работу. Некоторое количество тепла должно быть передано радиатору.

Что такое Неравенство Клаузиуса?

Неравенство Клаузиуса утверждает, что для термодинамического цикла, обменивающегося теплом с внешними резервуарами и подвергающегося термодинамическому циклу, линейный интеграл от (Q/Tsurr) меньше или равен нулю.

Математически мы можем записать неравенство Клаузиуса как:

где,

del Q — бесконечно малое количество тепла, поглощаемого системой.

Цурр — температура окружающей среды

Урок физики в 8-м классе по теме «КПД теплового двигателя»

Цели:

• Образовательная:
  Привитие интереса к предмету.
  
  Демонстрация применимости в жизни знаний, получаемых на различных уроках.
  
  
  Вовлечение каждого ученика в активный познавательный процесс.
  
  Выработка предметных компетенций.
• Воспитательная: воспитание внимательного, доброжелательного
  отношения к ответам одноклассников.
• Развивающая:
  развитие умений и способностей учащихся работать самостоятельно;
  
  расширение кругозора;
  
  повышение эрудиции;
  
  Развивать умения творчески подходить к решению задач;
  
  Развитие умений выступления перед аудиторией.

Структура урока:

1. Постановка учебной цели.
2. Повторение пройденного материала.
3. Изучение нового материала.
4. Закрепление изученного.
5. Домашнее задание.

Оборудование:

• мультимедиа;
• презентация PowerPoint

Ход урока

I. Организационный момент.

II. Повторение пройденного материала.

На прошлом уроке мы с вами разобрали понятия тепловых машин, их виды и
краткую историю развития. Давайте вкратце повторим пройденный материал, но
сначала послушаем сообщения, которые вы подготовили.

История ДВС (Презентация. Слайд
1). Сообщение учащегося “Первые тепловые машины”.

Слайд 2

1. Какие устройства называются тепловыми двигателями? (Машины, в которых
   внутренняя энергия топлива превращается в механическую энергию, называются
   тепловыми двигателями.)
2. Можно ли огнестрельное оружие отнести к тепловым двигателям? (Да.
   Энергия сгоревшего пороха переходит в механическую энергию снаряда.)
3. Можно ли человеческий организм отнести к тепловым двигателям? (Да.)
4. Почему ДВС не используются в подводных лодках при подводном плавании?
   (Под водой для работы двигателя внутреннего сгорания необходим воздух, а его
   там нет, либо необходимо брать сжиженный воздух, но это нерентабельно и
   усложняет процесс.)
5. Изменяется ли температура пара в турбине? (Да, она уменьшается.)
6. Все ли тепловые двигатели одинаково рентабельны? (Нет, не все, есть
   более экономичные, например дизельный двигатель. )

III. Изучение нового материала.

Обычно, рентабельность двигателей определяется их КПД.
(Коэффициентом полезного действия.)

Слайд 3

Физический словарик.

Коэффициент (от лат coefficientis) обычно постоянная или
известная величина – множитель при переменной или известной величине./

??? Что мы называли коэффициентом полезного действия при изучении механики?
(Отношение полезной работы к работе затраченной.)

(h = А _п / А_з
записать формулу на доске).

При работе тепловых двигателей механическая работа совершается за счет
превращения внутренней энергии горения топлива в механическую энергию.

Т.е.
то,
производя математические преобразования основной формулы ή получим новые формулы
для расчета КПД теплового двигателя: (учащиеся на местах, а затем у доски
производят необходимые преобразования).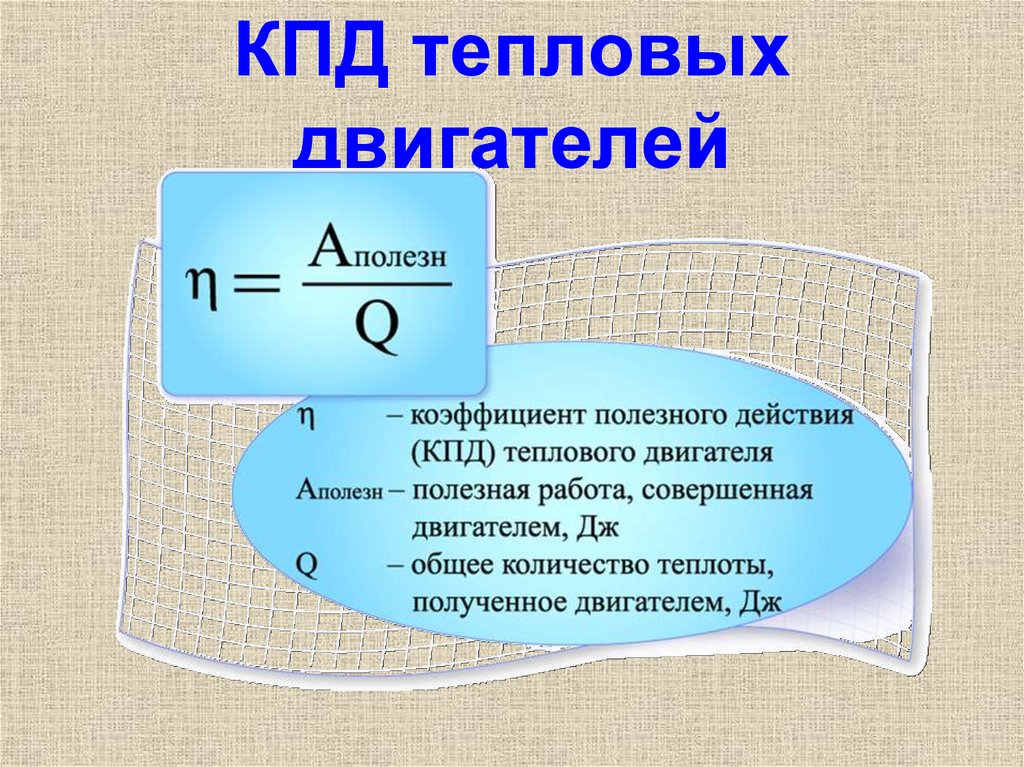

Совершая работу, тепловой двигатель использует лишь некоторую часть той
энергии, которая выделяется при сгорании топлива.

Физическая величина, показывающая, какую долю составляет совершаемая
двигателем работа от энергии, полученной при сгорании топлива, называется
коэффициентом полезного действия теплового двигателя.

КПД теплового двигателя находят по формуле

где Q – количество теплоты, полученное в результате сгорания топлива; А –
работа, совершаемая двигателем.

Задание: стр. 56–57 учебника, найти определение и формулу для расчета
КПД теплового двигателя. В чем сходство или отличие данных понятий?

Кроме того КПД теплового двигателя можно вычислять по формулам:

Слайд 4

Рассмотрим характеристики некоторых, наиболее используемых тепловых
двигателей

Характеристики тепловых двигателей (Слайд 5)

??? Как вы думаете, на что тратится большая часть внутренней энергии
тепловых двигателей?

??? Безопасны ли тепловые двигатели с точки зрения экологии?

Вы правы и это хорошо видно из следующих данных:

Применение тепловых машин и проблемы охраны
окружающей среды (Слайд 6)

При сжигании топлива в тепловых машинах требуется большое количество
кислорода. На сгорание разнообразного топлива расходуется от 10 до 25% кислорода,
производимого зелеными растениями.

Тепловые машины не только сжигают кислород, но и выбрасывают в атмосферу
эквивалентные количества двуокиси углерода (углекислого газа). Сгорание топлива
в топках промышленных предприятий и тепловых электростанций почти никогда не
бывает полным, поэтому происходит загрязнение воздуха золой, хлопьями сажи.
Сейчас во всем мире обычные энергетические установки выбрасывают в атмосферу
ежегодно 200–250 млн. т золы и около 60 млн. т диоксида
серы.

Кроме промышленности воздух загрязняет и транспорт, прежде всего
автомобильный (жители больших городов задыхаются от выхлопных газов
автомобильных двигателей).

IV. Закрепление.

Качественные задачи: (Слайд 7)

1. Один из учеников при решении получил ответ, что КПД
теплового двигателя равен 200%. Правильно ли решил ученик задачу? (Нет.
КПД теплового двигателя не может быть больше 100% или равен 100%)

2. КПД теплового двигателя 45%. Что означает это число?
(45% энергии идет на совершение полезной работы, а 55% энергии тратится
впустую на обогрев атмосферы, самого двигателя и т.д.)

3. Может ли КПД теплового двигателя быть равен 1,8;
50; 4; 90; 100%? (КПД теплового двигателя всегда меньше 100%)

4. Задача для любителей биологии: (Слайд 8)

В организме человека насчитывается около 600 мышц. Если бы все мышцы человека
напряглись, они вызвали бы усилие, равное приблизительно 25 т. считается, что
при нормальных условиях работы человек может развивать мощность 70–80 Вт, однако
возможна моментальная отдача энергии в таких видах спорта, как толкание ядра или
прыжки в высоту. Наблюдения показали, что при прыжках в высоту с одновременным
отталкиванием обеими ногами некоторые мужчины развивают в течение 0,1 с среднюю
мощность около 3700 Вт, а женщины – 2600 Вт.

КПД мышц человека равен 20%. Что это значит? Какую часть энергии мышцы тратят
впустую? (20% энергии тратится на полезную работу; 80% энергии мышцы
тратят впустую.)

5. Тепловой двигатель за цикл получает от нагревателя
энергию, равную 1000 Дж, и отдает холодильнику энергию 800 Дж. Чему равен КПД
теплового двигателя? (20%)

Попробуйте решить данную задачу самостоятельно, а в помощь я напомню вам
общую схему теплового двигателя. (Затем разобрать решение у доски).

6. Тепловой двигатель за цикл получает от нагревателя
энергию, равную 1000 Дж, и отдает холодильнику энергию 700 Дж. Чему равен КПД
теплового двигателя? (30%) (Решить самостоятельно.)

V. Итог урока (повторить основные понятия и формулы).

VI. Д/З

§ 24; вопросы на с. 57; индивидуальные карточки с задачами; всем желающим –
составить ребус или кроссворд по изученной теме.

Индивидуальные карточки домашнего задания:

К – 1.

1. Какое количество теплоты потребуется , чтобы расплавить 500 г льда,
   взятого при температуре -10 ºС, полученную воду довести до кипения и
   испарить 100 г воды? (620,5кДж)
2. Чему равен КПД плавильной печи, в которой на плавление 1 кг меди, взятой
   при температуре 85 ºС, расходуется 400 г каменного угля? (≈ 5,7%)

К – 2.

1. На нагревание и плавление меди израсходовано 1276 кДж теплоты.
   Определить массу меди, если ее начальная температура 15 ºС. (2 кг)
2. Какую массу антрацита надо сжечь в котле с КПД 40%, чтобы 1 т воды,
   поступающей в него при 20 ºС, нагреть до 100 ºС и половину превратить в пар
   при 100 ºС? (≈ 124 кг)

6.2: Двигатели и тепловая эффективность

1. Последнее обновление

2. Сохранить как PDF

• Том Вайдеман
• Калифорнийский университет, Дэвис

Простой двигатель

Циклические процессы позволяют иметь повторяющиеся способы преобразования тепловой энергии, поступающей в газ, в рабочую энергию, выходящую из газа.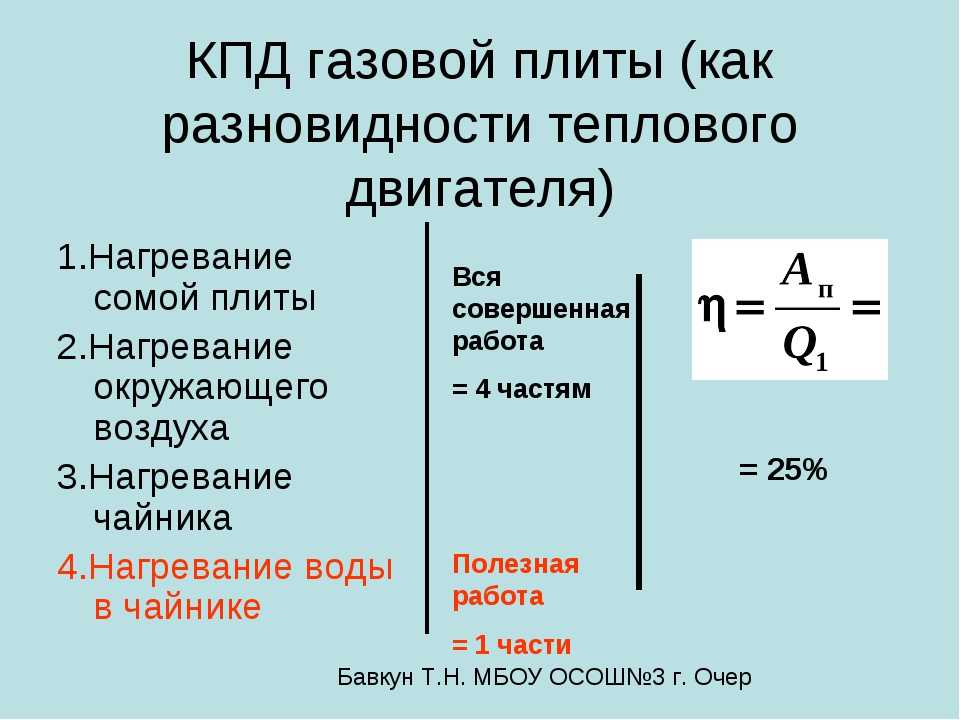 Мы знаем, что для теплообмена должна существовать разница температур, и правильно спроектированное устройство может работать в цикле, чтобы использовать разницу температур для получения полезной механической энергии. Такое устройство называется тепловой машиной . Конечно, для этого требуется циклический процесс, который проходит по часовой стрелке на диаграмме \(PV\). Теперь мы рассмотрим простейший вариант двигателя, который образует прямоугольник на своей диаграмме \(PV\). Мы будем делать акцент на том, чтобы визуализировать каждый этап цикла как физический процесс, в котором поршень обменивается теплом с тепловым резервуаром и/или взаимодействует с окружающей средой.

Рисунок 6.2.1 – Простой двигатель энергия не меняется в течение цикла, а это означает, что выходящая энергия работы (равная площади, ограниченной контуром) равна входящей тепловой энергии.

\[\Delta U = 0\; \;\;\Правая стрелка\;\;\; Q_{in} = W_{out} = \left(P_2-P_1\right)\left(V_2-V_1\right) \]

Теперь мы вычислим тепло, переданное во время всех четырех отдельных этапов циклического процесса, чтобы подтвердить этот результат. При этом мы будем включать диаграмму того, что происходит физически.

Рисунок 6.2.2a – Процесс A–B

это чуть теплее, чем газ в двигателе на каждом этапе процесса). Температура газа в процессе повышается, а объем увеличивается, при этом в систему поступает тепло. Количество переданного тепла:

\[Q_{AB} = nC_P\Delta T_{AB} = nC_P\left(\dfrac{P_2\Delta V_{AB}}{nR}\right)=\left(\dfrac{C_P}{R} P_2 \ right) \ left (v_2-v_1 \ right) \]

Рис. 6.2.2b-Процесс B-C

33

3333

333333 годы. и поскольку давление падает, это должно быть потому, что падает температура. Это может происходить только при неизменном объеме, когда тепло уходит из системы, а так как процесс квазистатический, то температура теплового резервуара на протяжении всего процесса несколько ниже температуры газа. Потеря тепла на этом этапе составляет:

\[Q_{BC} = nC_V\Delta T_{BC} = nC_V\left(\dfrac{\Delta P_{BC}V_2}{nR}\right)=\left(\dfrac{C_V}{R} V_2 \ справа) \ слева (P_1-P_2 \ Right) \]

Рис. 6.2.2C-Процесс C-D

Это Третий Лей. , на этот раз с падением температуры и объема. Опять же, этот квазистатический процесс требует, чтобы температура резервуара оставалась немного ниже температуры газа. Потери тепла:

\[Q_{CD} = nC_P\Delta T_{CD} = nC_P\left(\dfrac{P_2\Delta V_{CD}}{nR}\right)=\left(\dfrac{C_P}{R} P_1\right)\left(V_1-V_2\right) \]

температура за счет тепла, подведенного из термального резервуара, немного выше температуры газа. Передаваемое тепло:

\[Q_{DA} = nC_V\Delta T_{DA} = nC_V\left(\dfrac{\Delta P_{DA}V_1}{nR}\right)=\left(\dfrac{ C_V}{R}V_1\справа)\слева(P_2-P_1\справа) \]

Читателю предлагается в качестве упражнения по алгебре продемонстрировать, что сумма этих четырех теплопередач равна общей теплопередаче, как указано в уравнении 6. 2.1. При выполнении этого упражнения будет полезно помнить, что \(C_P = C_V + R\).

Двигатели реального мира

В ходе приведенных выше расчетов читателю могло прийти в голову, что постоянно возникало одно неудобное требование — тепловой резервуар всегда должен иметь бесконечно малую величину, отличную от температуры газа в двигателе. Как именно человек совершает такой подвиг? Резервуар становится немного теплее, увеличивая температуру газа до тех пор, пока они не придут к тепловому равновесию, затем резервуар снова становится немного теплее, так что он снова может отдавать небольшое количество тепла газу, и так далее? Этот процесс, очевидно, не может быть разумно сконструирован, и даже если бы это было возможно, тот факт, что скорость теплового потока связана с разницей температур, означает, что он будет мучительно медленным.

В реальном мире у нас обычно есть два термальных резервуара с фиксированными температурами для работы: один с высокой температурой, от которого двигатель получает тепло, и один с низкой температурой, куда двигатель отводит тепло. Обратите внимание, что в приведенном выше простом двигателе газ должен был как получать, так и отдавать тепло, хотя он получил чистое количество тепла, которое он преобразовал в работу. Это оказывается необходимой характеристикой всех двигателей (по причинам, которые мы рассмотрим позже) — двигатель не может просто брать тепло из одного горячего теплового резервуара и преобразовывать его в работу в цикле, не отдавая при этом тепло в другой. , более холодный термальный резервуар. Схема этого общего принципа двигателей показана ниже.

Рис. 6.2.3 – Реальная схема теплового двигателя Во-первых, процесс должен быть циклическим, что означает, что общее изменение внутренней энергии равно нулю, а общее поступающее тепло (тепло, поступающее из более теплого резервуара за вычетом тепла, отводимого в более холодный резервуар) равняется полной работе, которую необходимо совершить. выходит (технически есть еще работа, которая приходит, но эта схема включает только net работают, при этом отделяя «входящее» тепло от «исходящего» по причинам, которые вскоре станут ясны).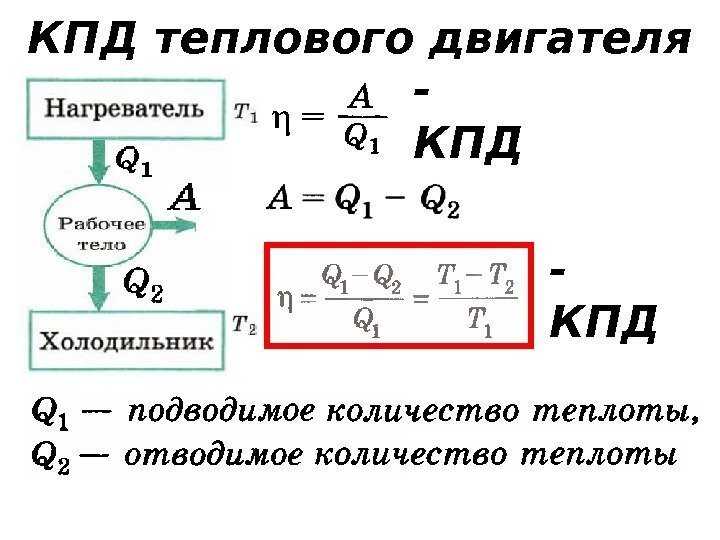 Мы включили теплоты, обмениваемые с двумя резервуарами, в терминах их абсолютных значений, так что нам не нужно заботиться о условном обозначении подвода/отвода тепла. Ясно, что произведенная работа представляет собой разность общей тепловой энергии, поступающей из горячего резервуара, за вычетом общей тепловой энергии, отводимой в холодный тепловой резервуар.

Тепловая эффективность

Это правда, что в реальном мире когда мы берем тепло из одного резервуара и отдаем его в другой, более холодный, мы делаем два резервуара немного ближе по температуре. В идеале мы хотели бы избежать «траты впустую» любой из этой исходящей тепловой энергии, которая не делает ничего, кроме повышения температуры более холодного резервуара, а вместо этого просто преобразовать всю тепловую энергию, поступающую из горячего резервуара, непосредственно в работу. Достижение этой цели означало бы создание «совершенно эффективного двигателя», и мы бы сказали, что он имеет тепловой КПД 100%. Таким образом, определение процентной эффективности любого двигателя довольно очевидно — просто возьмите отношение извлекаемой работы к подведенному теплу:

\[ e = \dfrac{W_{net}}{Q_H} = \dfrac{\left|Q_H \right|-\left|Q_C\right|}{\left|Q_H\right|} = 1 — \dfrac{\left|Q_C\right|}{\left|Q_H\right|}\]

Должно следует отметить, что «извлеченная работа» — это чистая работа — работа, которая выходит в течение полного цикла, за вычетом вложенной работы (т. е. это площадь внутри замкнутого контура на PV-диаграмме по часовой стрелке). Заметьте также, что для этого двигателя температура не просто немного выше температуры газа в двигателе, и на самом деле сила, вызванная давлением газа, ненамного больше, чем внешняя сила, когда совершается работа. Таким образом, ни один из этих процессов не является квазистатическим. Но, как мы видели, это не помешает нам эффективно использовать модели квазистатических процессов.

Позже мы увидим, что двигатели максимально эффективны, когда процессы, за которыми они следуют, являются обратимыми, но, конечно, для некоторых процессов это требует, чтобы вовлеченный тепловой резервуар изменял свою температуру, чтобы оставаться бесконечно мало больше или меньше, чем температура двигателя. Это противоречит самому понятию «теплового резервуара», поэтому ясно, что реальный КПД двигателя будет хуже, чем у реверсивных двигателей, которые мы можем использовать для их моделирования. Тем не менее, мы можем использовать отношение общей работы к общему теплу для обратимой модели, чтобы вычислить максимальная возможная эффективность для смоделированного двигателя.

Пример \(\PageIndex{1}\)

В циклическом процессе для двигателя, показанного ниже, процесс от A до B увеличивает давление втрое, процесс от B до C является адиабатическим, а рабочий газ в двигатель одноатомный. Вычислите максимальный тепловой КПД этого двигателя.

Раствор

Обозначим объем газа на изохорном участке (\(A\стрелка вправо B\)) \(V_o\). Мы можем использовать адиабатический процесс, чтобы связать объем, занимаемый газом в точке С, с \(V_o\): 9{\ frac {3} {5}}V_o \right)\right] = -0,933P_oV_o \end{массив}\right\}\;\;\;\Rightarrow\;\;\; W_{net}=W_1+W_2 = 0,667P_oV_o\номер\]

Тепло уходит из системы во время изобарического процесса, а во время адиабатического процесса тепло не обменивается, поэтому все тепло, поступающее в двигатель, поступает во время изохорного процесса, и это легко вычислить для одноатомного идеального газа:

\[Q_{in} = \frac{3}{2}\Delta P V = 3P_oV_o \nonnumber\]

Эффективность определяется отношением полезной работы к теплу:

\[e = \dfrac{W_{net}}{Q_{in}} = \dfrac{0,667P_oV_o}{3P_oV_o} = 22,2\% \nonumber\]

 

Цикл Отто

Наш самый узнаваемый тип двигателя — это двигатель внутреннего сгорания, и наиболее распространенный циклический процесс, которому они следуют, называется Цикл Отто .

Предупреждение

В дальнейшем, когда слово «газ» относится к газу внутри поршня, который в основном представляет собой воздух. Говоря о бензине (наиболее распространенном топливе для сжигания топлива), мы будем называть его в этой длинной форме — мы не будем использовать сокращенную версию «газ».0169

Мы начнем с того, что построим диаграмму \(PV\), которая аппроксимирует процесс, а затем объясним каждую часть цикла.

Рис. 6.2.4-Цикл OTTO

Процесс A-B (Adiabatic Compression)

Процесс A-B (Adiabatic Compression)

Процесс A-B (Adiabatic Compression)

Процесс A-B (Adiabatic) с Aniabress) с Aniabress) с Aniabress). Среда ENTARERSALE). СМЕРИБА ИЛИ САМАЛИВА И ОРИКАЛЬНОЕ СОЦИАЛА). при прохладной (окружающей) температуре, когда над смесью совершается работа по ее сжатию. Это происходит очень быстро, так что газ не успевает обмениваться теплом с окружающей средой, что и побуждает рассматривать этот процесс как адиабатический.

процесс B-C (изохорный нагрев)

Бензин воспламеняется, что быстро изменяет температуру газа внутри поршня. Технически тепло поступает не снаружи двигателя, а скорее в результате экзотермического химического процесса, но это одно и то же. Это воспламенение происходит очень внезапно, прежде чем газ успеет расширить поршень, поэтому мы рассматриваем этот процесс как изохорный.

процесс C-D (адиабатическое расширение)

Нагретый газ теперь находится под очень высоким давлением, и это давление расширяет поршень, совершая работу. Опять же, скорость этого процесса настолько велика, что очень мало тепла успевает выйти из поршня, когда он происходит, поэтому мы рассматриваем этот процесс как адиабатический.

процесс D-A (изохорное охлаждение)

После полного расширения охлажденный, но еще более горячий, чем окружающая среда газ выбрасывается из двигателя, и в камеру поступает новая порция воздуха и паров бензина. Технически газ не «охлаждается изохорически», но это равносильно тому, что камера вскоре заполняется новым газом с более низкой температурой и тем же объемом.

Этот пример показывает, как мы можем использовать то, что мы узнали о термодинамических процессах, для анализа реальных ситуаций, даже если наше понимание основано на идеальных ситуациях, которых не существует в реальном мире. Мы просто смотрим на особенности реального процесса и максимально приближаем его к квазистатическому процессу. Во время этого процесса «сопоставления» мы заботимся о том, чтобы конечные точки совпадали правильно (поскольку это состояния равновесия) и чтобы тепло/работа, передаваемые во время процесса, имели смысл. В приведенном выше примере это состояло в том, чтобы спросить, произошел ли процесс быстро (нет времени для отвода тепла) или не изменился ли объем (нет выполненной работы). Вскоре мы снова увидим другую форму этого сопоставления.

Давайте посмотрим на эффективность этого цикла. Имейте в виду, что наша идеализированная версия будет более эффективной, чем то, что мы можем достичь в реальном мире, но это дает нам верхний предел того, на что мы можем надеяться. Чтобы получить КПД, нам нужно тепло, отдаваемое горячим резервуаром, и тепло, забираемое холодным резервуаром. В этом цикле теплообмен происходит только во время процессов B-C и DA, которые оба являются изохорными, поэтому теплообмен пропорционален изменениям температуры. Таким образом, эффективность определяется выражением:

\[e = 1 — \dfrac{\left|Q_C\right|}{\left|Q_H\right|} = 1 — \dfrac{nC_V\left(T_D — T_A\right)}{nC_V\left( T_C — T_B\right)} = 1 — \dfrac{\left(T_D — T_A\right)}{\left(T_C — T_B\right)} \]

Из этого результата должно быть ясно, что двигатель работает больше эффективно, когда разница температур между двумя тепловыми резервуарами больше. В данном случае это разница между температурой впрыскиваемого газа и воспламененного газа. Из диаграммы должно быть ясно, что эта разница может быть измерена как разность (или, правильнее сказать, отношение) двух объемов, занимаемых газом. С практической точки зрения, газ нельзя сжать до минимального объема, прежде чем воспламенить его, потому что повышение температуры из-за сжатия само по себе может самопроизвольно воспламенить газ. Топливо с более высоким октановым числом обеспечивает большую степень сжатия без нежелательного самовоспламенения, что повышает эффективность.

Как мы можем сделать вывод из вышеизложенного, КПД этого двигателя можно переписать в терминах переменной, которую нам легче измерить, чем температуры, а именно свойства самого двигателя. Два из четырех процессов являются изохорными, что означает, что объем изменяется только дважды в течение всего цикла, что означает, что нам нужно беспокоиться только о двух объемах — максимальном и минимальном. Максимум возникает при полном расширении поршня, а минимум при его полном сжатии. Нас даже не волнует, каковы эти значения, когда дело доходит до эффективности, а все, что нас волнует, это 9{1-\gamma}\]

Цикл Дизеля

Небольшим изменением цикла Отто можно несколько повысить КПД. Это изменение заключается в управлении процессом воспламенения таким образом, чтобы он происходил при постоянном давлении, а не при постоянном объеме. В этой конструкции двигателя используется так называемый дизельный цикл . Это, конечно, означает, что воспламенение должно происходить менее «взрывно», что снижает скорость, с которой может произойти цикл, и мы знаем из Физики 9А, что скорость, с которой производится работа, является мощностью цикла, поэтому, хотя это цикл получается более эффективным, он обеспечивает меньшую мощность.

Чтобы определить разницу в эффективности, нужно только изменить знаменатель уравнения 6.2.7, учитывающего процесс воспламенения (с B на C). Вместо того, чтобы происходить при постоянном объеме, это происходит при постоянном давлении, что просто изменяет \(C_V\) на \(C_P\), что дает:

\[e = 1-\dfrac{C_V\left(T_D-T_A\ right)}{C_P\left(T_C-T_B\right)}=1-\dfrac{1}{\gamma}\;\dfrac{T_D-T_A}{T_C-T_B}\]

Член, который вычитается из эффективность снижается на гамма-фактор, что приводит к более высокой эффективности. Кроме того, возможны более высокие степени сжатия, поскольку воздух сжимается без топлива (топливо добавляется постепенно, используя топливных форсунок в процессе воспламенения, поддерживая постоянное давление), устраняя проблему воспламенения топлива при сжатии. Конечно, хотя много лет назад этот процесс применялся исключительно для дизельных двигателей, в настоящее время впрыск топлива и сопровождающая его более высокая степень сжатия являются стандартом для автомобилей, работающих на бензине.

Цикл Карно

Мы смогли грамотно описать циклы Отто и Дизеля в терминах 4 квазистатических процессов, рассматривая воспламенение газа так, как если бы тепло добавлялось, а не возникало в результате химической реакции, и рассматривая замещение газа, как будто выделяется тепло. Без этих приемов сохранение квазистатических процессов сделало бы их очень медленными и не могло бы происходить между резервуарами с двумя фиксированными температурами, как показано на рис. чтобы и изохорический, и изобарический процессы происходили квазистатически, температура резервуара должна изменяться таким образом, чтобы она лишь бесконечно мало отличалась от температуры газа. Мы не можем получить что-то даром, и на самом деле процессы воспламенения и замещения газа необратимы, что делает эти процессы лишь приблизительно квазистатическими циклами, которые мы объявили.

Из этого анализа мы видим, что проблема с включением изохорных и изобарических процессов в «реальный» случай двигателя, вынужденного работать между двумя резервуарами с фиксированными температурами, заключается в том, что мы не можем сделать эти процессы обратимыми. Но даже при этом фиксированном температурном ограничении резервуаров есть два процесса, которые мы можем (в принципе) выполнять квазистатически. Адиабатический процесс вообще не включает теплопередачу, поэтому относительная температура двигателя и резервуара не имеет значения. Изотермический процесс оставляет температуру двигателя неизменной, поэтому, если она равна температуре резервуара, проблем не возникает.

В обсуждении, последовавшем за уравнением 5.8.20, мы отметили, что в любой данной точке на PV-диаграмме газа адиабата, проходящая через эту точку, круче, чем изотерма, которая также проходит через нее. Из-за этого мы можем создать циклический процесс, в котором используются два изотермических процесса (один вверху, один внизу диаграммы PV) и два адиабатических процесса (по одному на каждой стороне диаграммы PV), и этот цикл может быть приводимый в движение двумя резервуарами с фиксированной температурой. Это известно как Цикл Карно .

Рисунок 6.2.5 – Цикл Карно Отметив, что теплота не передается во время двух адиабатических процессов, и используя уравнение 5.8.16 для теплоты, переданной во время двух изотермических процессов, мы имеем:

\[ \left. \begin{массив}{l} \left|Q_H\right| = W_{out} = nRT_H\ln\left[\dfrac{V_B}{V_A}\right] \\ \left|Q_C\right| = -W_{in} = -nRT_C\ln\left[\dfrac{V_D}{V_C}\right]=nRT_C\ln\left[\dfrac{V_C}{V_D}\right] \\ e = 1 — \ dfrac{\left|Q_C\right|}{\left|Q_H\right|} \end{массив} \right\} \;\;\;\Rightarrow\;\;\; e = 1-\dfrac{T_C}{T_H}\dfrac{\ln\left[\dfrac{V_C}{V_D}\right]}{\ln\left[\dfrac{V_B}{V_A}\right]} \] 9{\gamma-1} \end{массив} \right\} \;\;\;\Rightarrow\;\;\; \dfrac{V_B}{V_A} = \dfrac{V_C}{V_D}\]

Подстановка их выше приводит к сокращению логарифмов в числителе и знаменателе, что делает эффективность цикла Карно простой функцией температур два резервуара:

\[e=1-\dfrac{T_C}{T_H} \]

Чем больше разница температур между двумя резервуарами, тем выше КПД двигателя Карно.

Холодильники

Одна вещь, которую мы постоянно видели в нашем обсуждении двигателей, это то, что циклы идут по часовой стрелке на диаграмме PV . Это гарантирует, что после полного цикла из системы выйдет работы из , а из тепла выйдет из . Что произойдет, если мы запустим цикл в обратном порядке? Затем идет работа и уходит тепло. Это основа холодильника . Естественно, это не значит, что мы можем взять двигатель внутреннего сгорания, включить его «задним ходом», и он превратится в кондиционер. Во-первых, мы не можем «не воспламенить» газ. Но мы можем осуществлять процессы в обратном направлении другими средствами. Во-первых, давайте посмотрим на схему холодильника, как мы сделали это для тепловой машины:

Рисунок 6.2.6 – Реальная схема холодильника состоит в том, чтобы отвести как можно больше тепла от холодного резервуара, совершая при этом как можно меньше работы. Поэтому мы определяем коэффициент полезного действия как отношение отводимой теплоты к требуемой работе:

\[K=\dfrac{\left|Q_C\right|}{W}=\dfrac{\left|Q_C\right|}{\left|Q_H\right|-\left|Q_C\right|}\ ]

Чрезвычайно упрощенный способ представить себе, как работает холодильник, таков: мы знаем, что если мы очень резко сожмем газ, он станет намного горячее (см.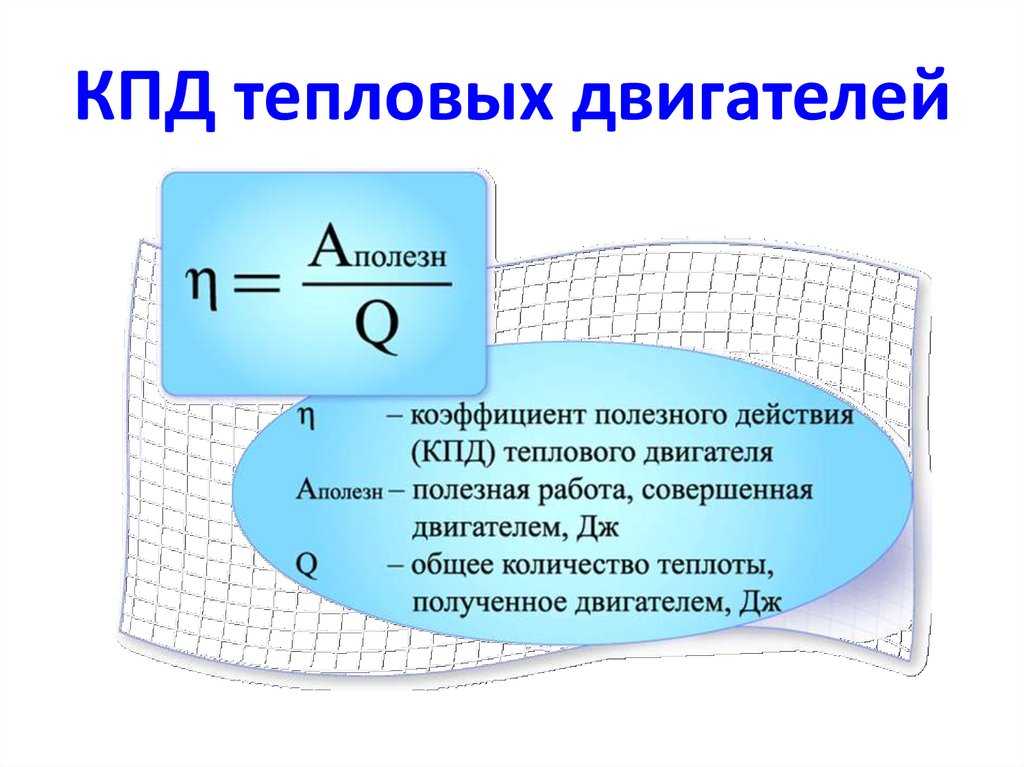 пример в самом конце раздела 5.8). Неудивительно, что верно и обратное: резкое расширение поршня газом приводит к сильному охлаждению газа. Предположим, мы хотим, чтобы внутри холодильника было холоднее, чем снаружи (да, это определение холодильника!). Начните с газа в поршне вне холодильника, сожмите его до небольшого объема и подождите сжатым, пока он не достигнет температуры наружного воздуха. Затем резко отпустите поршень и быстро отнесите его в холодильник. Если мы сожмем его достаточно, изменение температуры газа в поршне сделает его температуру ниже температуры внутри холодильника. Подождем немного, пока внутренняя часть холодильника отдает тепло холодному воздуху в поршне, тем самым охлаждая воздух внутри холодильника. Когда они достигают равновесия, мы выносим поршень наружу и повторяем процесс. Это транспортирует тепловую энергию из холодильника.

Работа, совершаемая газом при сжатии, превышает работу, совершаемую газом при расширении (т.е. необходимо приложить чистую работу). Процессы сжатия и расширения являются адиабатическими, а процессы «ожидания» — изохорными, поэтому PV-диаграмма выглядит примерно так:

Очевидно, мы пожертвовали реальностью ради этого понятного «холодильника». Очевидно, что нам не нужно транспортировать поршень в охлаждаемую камеру и из нее, и вместо этого мы можем подавать газ в нее и из нее, сжимая его на выходе и расширяя на входе. Но есть еще довольно большая проблема с этой конструкцией. Для того чтобы тепло передавалось в нужных направлениях в нужные моменты времени, нам нужно, чтобы температура газа после его охлаждения от расширения была ниже температуры окружающей среды в холодильнике. PV температуры внутри и снаружи холодильников более или менее соответствуют температурам состояний B и D соответственно. Это означает, что если мы проведем изотермы через точки B и D , то разрыв между этими изотермами представляет собой максимальный температурный разрыв, который мы можем поддерживать между горячей и холодной областями. Очевидно, это зависит от разницы давлений, которую мы можем создать между сжатым газом и расширенным газом, но с практической точки зрения это является существенным препятствием.

Способ преодоления этого ограничения состоит в переносе большей части тепловой энергии в фазу хладагента. Мы знаем, что мы можем менять фазы, комбинируя сжатие/расширение и нагрев/охлаждение жидкости, а скрытая теплота парообразования значительна по сравнению с удельной теплоемкостью при небольшом изменении температуры. Это приводит к следующему основному процессу:

• компрессор превращает хладагент в жидкую фазу, которая нагревает его выше температуры наружного воздуха
• затем жидкость поступает в змеевик конденсатора , целью которого является увеличение площади контакта с наружным воздухом, ускорение процесса сброса тепла
• к тому времени, когда жидкость прошла через змеевик конденсатора, она находится под высоким давлением, но пришла в термическое равновесие с наружным воздухом, а затем проходит в расширительный клапан , где она адиабатически расширяется, изменяя фазу назад к газу и значительному падению температуры ниже температуры внутреннего воздуха
• затем газ проходит через змеевик испарителя , что увеличивает скорость, с которой тепло может попасть в хладагент из внутреннего воздуха, и в конце змеевика испарителя он снова поступает в компрессор, чтобы снова запустить цикл.

---

Эта страница под названием 6.2: Двигатели и тепловая эффективность распространяется по лицензии CC BY-SA 4.0 и была создана, изменена и/или курирована Томом Вайдеманом непосредственно на платформе LibreTexts.

1. Наверх
• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Том Вайдеман

   Лицензия

   CC BY-SA

   Версия лицензии

   4,0

   Показать оглавление

   нет

2. Теги

   1. тепловая машина
   2. источник@родной
   3. Тепловой КПД

Калькулятор эффективности Карно

Если вы интересуетесь термодинамикой, вам обязательно стоит попробовать этот калькулятор эффективности Карно. Это удобный инструмент, который поможет вам определить тепловой КПД двигателя, работающего по циклу Карно. Продолжайте читать, чтобы узнать, что такое цикл Карно, как решить уравнение эффективности Карно и почему вам не следует использовать этот тип двигателя в своем автомобиле.

Что такое тепловая машина Карно?

Тепловая машина Карно работает по циклу Карно , наиболее эффективному процессу тепловой машины, допускаемому законами термодинамики. В этом цикле двигатель проходит четыре последовательных процесса, после чего возвращается в исходное состояние.

Сам двигатель состоит из двух неподвижных тел и рабочего тела (жидкого или парового тела). Два неподвижных тела имеют постоянные температуры:

• Первая (называемая «печь») имеет высокую температуру ThT_\text{h}Th​.
• Второй (называемый «холодильник») имеет низкую температуру TcT_\text{c}Tc​.

Цикл Карно. Его четыре шага (пронумерованные 1, 2, 3 и 4 на рисунке) объясняются в абзаце ниже.

Четыре фазы цикла Карно:

1. Изотермическое расширение при ThT_\text{h}Th​. Рабочее тело при постоянной температуре ThT_\text{h}Th​ расширяется, совершая работу над окружающей средой.
2. Адиабатическое расширение . Рабочее тело расширяется дальше, совершая работу над окружающей средой, но теряет часть своей внутренней энергии. Потеря энергии означает охлаждение до температуры TcT_\text{c}Tc​.
3. Изотермическое сжатие при TcT_\text{c}Tc​. Окружающая среда совершает работу над рабочим телом, сжимая его при постоянной температуре TcT_\text{c}Tc​. Поскольку давление ниже, чем на шаге 1, количество работы меньше, чем работа, произведенная тогда.
4. Адиабатическое сжатие . Окружающая среда продолжает воздействовать на рабочее вещество, еще больше сжимая его. Сжатие приводит к повышению температуры до ThT_\text{h}Th​. В конце шага 4 рабочее тело находится точно в том же состоянии, что и до шага 1.

Уравнение эффективности Карно

Двигатель Карно — это самый эффективный тепловой двигатель, который можно построить. Чтобы найти его КПД ηηη, нужно применить следующее уравнение:

η=(Th−TcTh)⋅100%\eta = \left(\frac{T_\text{h} — T_\text{c}}{T_\text{h}}\right) \cdot 100 \ %η=(Th​Th​−Tc​​)⋅100%

И ThT_\text{h}Th​, и TcT_\text{c}Tc​ являются абсолютными температурами (выраженными в градусах Кельвина).

Например, можно попробовать вычислить КПД Карно двигателя, работающего между двумя телами: одно при температуре 25 °C25\text{ °C}25 °C, а другое при 135 °C135\text{ ° С}135 °С. Чтобы найти результат, вам нужно выполнить следующие действия:

1. Используйте конвертер температуры, чтобы перевести 25 °C25\text{ °C}25 °C в градусы Кельвина. Вы также можете произвести расчеты вручную — в этом случае
   Tc=25+273,15=298,15 KT_\text{c} = 25 + 273,15 = 298,15\text{ K}Tc​=25+273,15=298,15 K

2. Повторите шаг 1 для температуры горячего резервуара. В этом случае
   Th=135+273,15=408,15KT_\text{h} = 135 + 273,15 = 408,15\text{K}Th​=135+273,15=408,15K

3. Введите эти значения в уравнение эффективности Карно:

 η=Th−TcTh⋅100%η=408,15−298,15408,15⋅100%η=110408,15⋅100%η=26,95%\quad\ \begin{align}
η &= \frac{T_\text{h} — T_\text{c}}{T_\text{h}} \cdot 100\% \\
η &= \frac{408,15 — 298,15}{408,15} \cdot 100\% \\
η &= \frac{110}{408,15} \cdot 100\% \\
η &= 26,95\%
\end{align} ηηηη​=Th​Th​−Tc​​⋅100%=408,15408,15−298,15​⋅100%=408,15110​⋅100%=26,95%​

4. Эффективность Карно равна 26,95% . Вы можете проверить результат с помощью нашего калькулятора теплового КПД!

Можно ли построить двигатель Карно?

Двигатель Карно представляет собой идеализированный случай тепловой машины. Тем не менее теоретически можно построить двигатель по модели двух резервуаров с постоянными температурами и рабочим телом.

Причина, по которой двигатель не имеет практического применения, заключается в длительности каждого процесса.