Формула КПД (коэффициента полезного действия) в физике

Формула КПД (коэффициента полезного действия) в физике

В реальной действительности работа, совершаемая при помощи какого — либо устройства, всегда больше полезной работы, так как часть работы выполняется против сил трения, которые действуют внутри механизма и при перемещении его отдельных частей. Так, применяя подвижный блок, совершают дополнительную работу, поднимая сам блок и веревку и, преодолевая силы трения в блоке.

Введем следующие обозначения: полезную работу обозначим $A_p$, полную работу — $A_{poln}$. При этом имеем:

\[A_p Определение и формула КПД

Определение

Коэффициентом полезного действия (КПД) называют отношение полезной работы к полной. Обозначим КПД буквой $\eta $, тогда:

\[\eta =\frac{A_p}{A_{poln}}\ \left(2\right).\]

Чаще всего коэффициент полезного действия выражают в процентах, тогда его определением является формула:

\[\eta =\frac{A_p}{A_{poln}}\cdot 100\%\ \left(2\right). \]

При создании механизмов пытаются увеличить их КПД, но механизмов с коэффициентом полезного действия равным единице (а тем более больше единицы) не существует.

И так, коэффициент полезного действия — это физическая величина, которая показывает долю, которую полезная работа составляет от всей произведенной работы. При помощи КПД оценивают эффективность устройства (механизма, системы), преобразующей или передающей энергию, совершающего работу.

Для увеличения КПД механизмов можно пытаться уменьшать трение в их осях, их массу. Если трением можно пренебречь, масса механизма существенно меньше, чем масса, например, груза, который поднимает механизм, то КПД получается немного меньше единицы. Тогда произведенная работа примерно равна полезной работе:

\[A_p\approx A_{poln}\left(3\right).\]

Золотое правило механики

Необходимо помнить, что выигрыша в работе, используя простой механизм добиться нельзя.

Выразим каждую из работ в формуле (3) как произведение соответствующей силы на путь, пройденный под воздействием этой силы, тогда формулу (3) преобразуем к виду:

\[F_1s_1\approx F_2s_2\left(4\right). \]

Выражение (4) показывает, что используя простой механизм, мы выигрываем в силе столько же, сколько проигрываем в пути. Данный закон называют «золотым правилом» механики. Это правило сформулировал в древней Греции Герон Александрийский.

Это правило не учитывает работу по преодолению сил трения, поэтому является приближенным.

КПД при передаче энергии

Коэффициент полезного действия можно определить как отношение полезной работы к затраченной на ее выполнение энергии ($Q$):

\[\eta =\frac{A_p}{Q}\cdot 100\%\ \left(5\right).\]

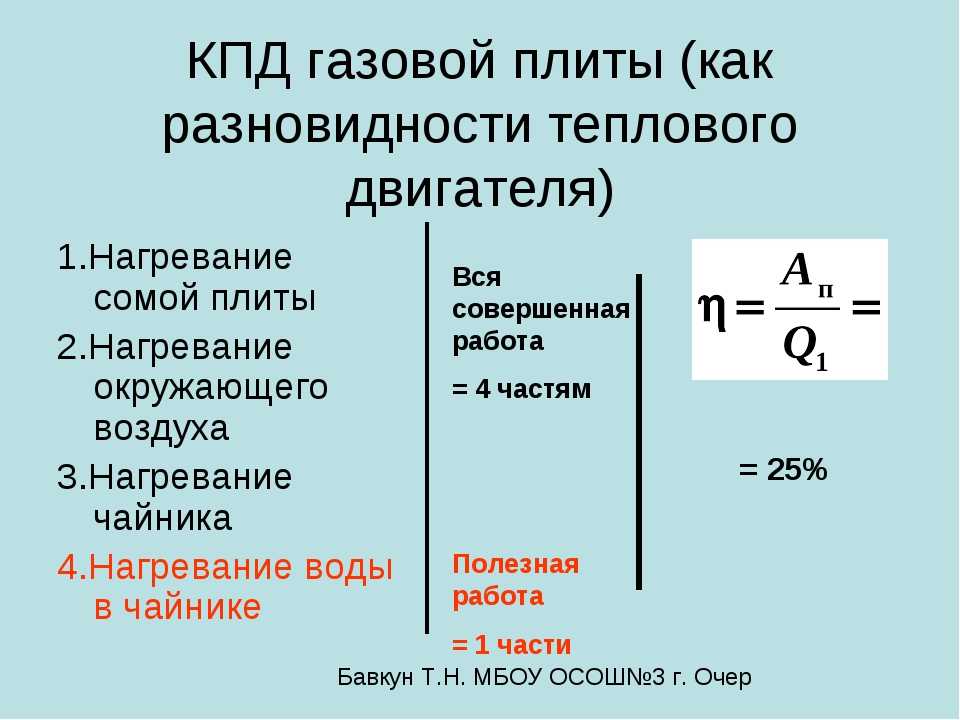
Для вычисления коэффициента полезного действия теплового двигателя применяют следующую формулу:

\[\eta =\frac{Q_n-Q_{ch}}{Q_n}\left(6\right),\]

где $Q_n$ — количество теплоты, полученное от нагревателя; $Q_{ch}$ — количество теплоты переданное холодильнику.

КПД идеальной тепловой машины, которая работает по циклу Карно равно:

\[\eta =\frac{T_n-T_{ch}}{T_n}\left(7\right),\]

где $T_n$ — температура нагревателя; $T_{ch}$ — температура холодильника.

Примеры задач на коэффициент полезного действия

Пример 1

Задание. Двигатель подъемного крана имеет мощность $N$. За отрезок времени равный $\Delta t$ он поднял груз массой $m$ на высоту $h$. Каким является КПД крана?\textit{}

Решение. Полезная работа в рассматриваемой задаче равна работе по подъему тела на высоту $h$ груза массы $m$, это работа по преодолению силы тяжести. Она равна:

\[A_p=mgh\ \left(1.1\right).\]

Полную работу, которая выполняется при поднятии груза, найдем, используя определение мощности:

\[N=\frac{A_{poln}}{\Delta t}\to A_{poln}=N\Delta t\left(1.2\right).\]

Воспользуемся определением коэффициента полезного действия для его нахождения:

\[\eta =\frac{A_p}{A_{poln}}\cdot 100\%\left(1.3\right).\]

Формулу (1.3) преобразуем, используя выражения (1. 1) и (1.2):

\[\eta =\frac{mgh}{N\Delta t}\cdot 100\%.\]

Ответ. $\eta =\frac{mgh}{N\Delta t}\cdot 100\%$

Пример 2

Задание. Идеальный газ выполняет цикл Карно, при этом КПД цикла равно $\eta $. Какова работа в цикле сжатия газа при постоянной температуре? Работа газа при расширении равна $A_0$

Решение. Коэффициент полезного действия цикла определим как:

\[\eta =\frac{A_p}{Q}\left(2.1\right).\]

Рассмотрим цикл Карно, определим, в каких процессах тепло подводят (это будет $Q$).

Так как цикл Карно состоит из двух изотерм и двух адиабат, можно сразу сказать, что в адиабатных процессах (процессы 2-3 и 4-1) теплообмена нет. В изотермическом процессе 1-2 тепло подводят (рис.1 $Q_1$), в изотермическом процессе 3-4 тепло отводят ($Q_2$). Получается, что в выражении (2. 1) $Q=Q_1$. Мы знаем, что количество теплоты (первое начало термодинамики), подводимое системе при изотермическом процессе идет полностью на выполнение газом работы, значит:

\[Q=Q_1=A_{12}\left(2.2\right).\]

Газ совершает полезную работу, которую равна:

\[A_p=Q_1-Q_2\left(2.3\right).\]

Количество теплоты, которое отводят в изотермическом процессе 3-4 равно работе сжатия (работа отрицательна) (так как T=const, то $Q_2=-A_{34}$). В результате имеем:

\[A_p=A_{12}+A_{34}\left(2.4\right).\]

Преобразуем формулу (2.1) учитывая результаты (2.2) — (2.4):

\[\eta =\frac{A_{12}+A_{34}}{A_{12}}\to A_{12}\eta =A_{12}+A_{34}\to A_{34}=(\eta -1)A_{12}\left(2.4\right).\]

Так как по условию $A_{12}=A_0,\ $окончательно получаем:

\[A_{34}=\left(\eta -1\right)A_0.\]

Ответ. $A_{34}=\left(\eta -1\right)A_0$

Читать дальше: формула линейной скорости.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Решение задач на КПД теплового двигателя | 8 класс

Содержание

КПД теплового двигателя рассчитывается по формуле $\eta = \frac{A_п}{Q_1}$ или $\eta = \frac{Q_1 — Q_2}{Q_1} \cdot 100 \%$, где
$A_п$ — полезная работа,
$Q_1$ — количество теплоты, полученное от нагревателя,
$Q_2$ — количество теплоты, отданное холодильнику.

Когда говорят о коэффициенте полезного действия теплового двигателя, часто используют понятие мощности или полезной мощности: $N = \frac{A_п}{t}$. Эту величину в жизни использовать удобнее, чем говорить о полезной работе. 

На данном уроке мы разберем решение задач, используя формулы, приведенные выше.

Для решения задач, в условиях которых, говорится о сжигании топлива ($Q = qm$), вам понадобятся табличные значения удельной теплоты сгорания топлива.

Задача №1

Какая работа совершена внешними силами при обработке железной заготовки массой $300 \space г$, если она нагрелась на $200 \degree C$?

Дано:
$m = 300 \space г$
$\Delta t = 200 \degree C$
$c = 460 \frac{Дж}{кг \cdot \degree C}$

СИ:
$m = 0.3 \space кг$

$A — ?$

Показать решение и ответ

Скрыть

Решение:

Для того чтобы нагреть железную деталь, необходимо сообщить ей некоторое количество теплоты:
$Q = cm(t_2 — t_1) = cm \Delta t$.

Рассчитаем эту энергию:
$Q = 460 \frac{Дж}{кг \cdot \degree C} \cdot  0.3 \space кг \cdot 200 \degree C = 27 \space 600 \space Дж = 27.6 \space кДж$.

Сообщенная энергия будет эквивалентна работе внешних сил:
$A = Q = 27.6 \space кДж$.

Ответ: $A = 27.6 \space кДж$.

Задача №2

Приняв, что вся тепловая энергия угля обращается в полезную работу, рассчитайте какого количества каменного угля в час достаточно для машины мощностью $733 \space Вт$?

Дано:
$t = 1 \space ч$
$N = 733 \space Вт$
$q = 2. 6}{86 \space 400} = 25 \space сут$.

Ответ: $t = 25 \space сут$.

5

Оценить урок

Поделиться уроком →

Что можно улучшить?

Изложение материала

Непонятное объяснение

Урок неполный, не хватает
информации

Урок перегружен, слишком много
информации

Тесты плохого качества

Тестов недостаточно

Тестов слишком много

Тесты слишком легкие

Тесты слишком сложные

Изображения

Изображения плохого качества

Изображений недостаточно

Изображений слишком много

Другое

Войдите, чтобы оценивать уроки

Что нужно исправить?

Спасибо, что помогаете нам стать лучше!

Проверим знания по теме?

КПД тепловых двигателей

Комментарии

Тепловая эффективность — Энергетическое образование

Энергетическое образование

Меню навигации

ИСТОЧНИКИ ЭНЕРГИИ

ИСПОЛЬЗОВАНИЕ ЭНЕРГИИ

ЭНЕРГЕТИЧЕСКОЕ ВОЗДЕЙСТВИЕ

ИНДЕКС

Поиск


Рисунок 1: Количество работы, произведенной для данного количества тепла, определяет тепловую эффективность системы. ^[1]

Тепловые двигатели превращают тепло в работу. Тепловой КПД выражает долю тепла, которая превращается в полезную работу. Тепловой КПД обозначается символом [math]\eta[/math] и может быть рассчитан по уравнению:

[математика]\eta=\frac{W}{Q_H}[/math]

Где:

[math]W[/math] — полезная работа и

[math]Q_H[/math] — общее количество подведенной тепловой энергии от горячего источника. ^[2]

Тепловые двигатели часто работают с эффективностью от 30% до 50% из-за практических ограничений. Тепловые двигатели не могут достичь 100% термического КПД ([математика]\эта = 1[/математика]) в соответствии со Вторым законом термодинамики. Это невозможно, потому что некоторое количество отработанного тепла всегда производится в тепловом двигателе, что показано на рисунке 1 термином [math]Q_L[/math]. Хотя полная эффективность тепловой машины невозможна, существует много способов повысить общую эффективность системы.

Пример

Если вводится 200 Дж тепловой энергии в виде тепла ([math]Q_H[/math]), а двигатель выполняет работу 80 Дж ([math]W[/math]), то КПД равен 80 Дж / 200 Дж, что составляет 40% КПД.

Тот же результат можно получить, измерив отработанное тепло двигателя. Например, если в двигатель вложено 200 Дж и наблюдается 120 Дж отходящего тепла, то должно быть выполнено 80 Дж работы, что дает КПД 40%.

Эффективность Карно

основной артикул

Существует максимально достижимая эффективность тепловой машины, которая была выведена физиком Сади Карно. Следуя законам термодинамики, уравнение для этого оказывается таким

[математика]\eta_{max}=1 — \frac{T_L}{T_H}[/math]

Где

[math]T_L[/math] — температура холодной «раковины»
и

[math]T_H[/math] — температура теплового резервуара.

Это описывает КПД идеализированного двигателя, которого в реальности достичь невозможно. ^[3] Из этого уравнения следует, что чем ниже температура стока [math]T_L[/math] или выше температура источника [math]T_H[/math], тем больше работы доступно для тепловой машины. Энергия для работы получается за счет уменьшения полной энергии жидкости, используемой в системе. Следовательно, чем больше изменение температуры, тем больше это уменьшение в жидкости и, следовательно, больше энергии, доступной для совершения работы. ^[4]

Для дополнительной информации

Для получения дополнительной информации см. соответствующие страницы ниже:

• Тепловая машина
• Сгорание углеводородов часто является источником тепла для этих двигателей.
• Солнечная тепловая электростанция
• Атомная электростанция
• Чтобы узнать о тепловом КПД автомобильных двигателей, нажмите здесь
• Или исследуйте случайную страницу!

Ссылки

1. ↑ Эта фотография была сделана командой Energy Education.
2. ↑ ТПУБ Механика двигателя. (4 апреля 2015 г.). Тепловой КПД [Онлайн]. Доступно: http://enginemechanics.tpub.com/14075/css/14075_141.htm
3. ↑ Гиперфизика, Цикл Карно [Онлайн], Доступно: http://hyperphysics. phy-astr.gsu.edu/hbase/thermo/carnot.html
4. ↑ Р. А. Хинрихс и М. Клейнбах, «Тепло и работа», в Energy: its Use and the Environment , 4th ed. Торонто, Онтарио. Канада: Thomson Brooks/Cole, 2006, ch.4, sec.E, pp.115.

Калькулятор эффективности Карно

Если вы интересуетесь термодинамикой, вам обязательно стоит попробовать этот калькулятор эффективности Карно. Это удобный инструмент, который поможет вам определяют тепловой КПД двигателя, работающего по циклу Карно . Продолжайте читать, чтобы узнать, что такое цикл Карно, как решить уравнение эффективности Карно и почему вам не следует использовать этот тип двигателя в своем автомобиле.

💡 Вас также может заинтересовать наш калькулятор эффективности и калькулятор коэффициента полезного действия.

Что такое тепловая машина Карно?

Тепловая машина Карно работает по циклу Карно , наиболее эффективному процессу тепловой машины разрешено законами термодинамики. В этом цикле двигатель проходит четыре последовательных процесса и после этого возвращается в исходное состояние.

Сам двигатель состоит из двух неподвижных тел и рабочего тела (жидкостного или парового тела). Два неподвижных тела имеют постоянные температуры:

• Первое тело (называемое «печью») имеет высокую температуру ThT_\text{h}Th​.
• Второй (называемый «холодильник») имеет низкую температуру TcT_\text{c}Tc​.

Цикл Карно. Его четыре шага (пронумерованные 1, 2, 3 и 4 на рисунке) объясняются в абзаце ниже.

Четыре фазы цикла Карно:

1. Изотермическое расширение при ThT_\text{h}Th​. Рабочее тело при постоянной температуре ThT_\text{h}Th​ расширяется, совершая работу над окружающей средой.

2. Адиабатическое расширение . Рабочее тело расширяется дальше, совершая работу над окружающей средой, но теряет часть своей внутренней энергии. Потеря энергии означает охлаждение до температуры TcT_\text{c}Tc​.

3. Изотермическое сжатие при TcT_\text{c}Tc​. Окружающая среда совершает работу над рабочим телом, сжимая его при постоянной температуре TcT_\text{c}Tc​. Поскольку давление ниже, чем на шаге 1, количество работы меньше, чем работа, произведенная тогда.

4. Адиабатическое сжатие . Окружающая среда продолжает воздействовать на рабочее вещество, еще больше сжимая его. Сжатие приводит к повышению температуры до ThT_\text{h}Th​. В конце шага 4 рабочее тело находится точно в том же состоянии, что и до шага 1.

Уравнение эффективности Карно

Двигатель Карно — это самый эффективный тепловой двигатель, который можно построить. Чтобы найти его эффективность ηηη, нужно применить следующее уравнение:

η=(Th−TcTh)⋅100%\eta = \left(\frac{T_\text{h} — T_\text{c}}{ T_\text{h}}\right) \cdot 100 \%η=(Th​Th​−Tc​)⋅100%

Оба ThT_\text{h}Th​ и TcT_\text{c}Tc​ — абсолютные температуры (выраженные в градусах Кельвина).

Например, можно попробовать вычислить КПД Карно двигателя, работающего между двумя телами: одно при температуре 25 °C25\text{ °C}25 °C, а другое при 135 °C135\text{ ° С}135 °С. Чтобы найти результат, вам нужно выполнить следующие шаги:

1. Используйте конвертер температуры, чтобы перевести 25 °C25\text{ °C}25 °C в градусы Кельвина. Вы также можете сделать расчеты вручную — в этом случае:

Tc=25+273,15=298,15 K\qquad\footnotesize T_\text{c} = 25 + 273,15 = 298,15\text{ K}Tc​=25+273,15=298,15 K

2. Повторите шаг 1 для температуры горячий резервуар. В данном случае:

Th=135+273,15=408,15 K\qquad\footnotesize T_\text{h} = 135 + 273,15 = 408,15\text{ K}Th​=135+273,15=408,15 K

3. Введите эти значения в уравнение эффективности Карно:

 η=Th−TcTh⋅100%η=408,15−298,15408,15⋅100%η=110408,15⋅100%η=26,95%\qquad\small \\begin{align}
η &= \frac{T_\text{h} — T_\text{c}}{T_\text{h}} \cdot 100\% \\[1em]
η &= \frac{408,15 — 298,15}{408,15} \cdot 100\% \\[1em]
η &= \frac{110}{408,15} \cdot 100\% \\[1em]
η &= 26,95\%
\end{align} ηηηη​=Th​Th​−Tc​​⋅100%=408,15408,15−298,15​⋅100%=408,15110​⋅100%=26,95%​

4. Эффективность Карно равна 26,95% .