Содержание
Характеристики двигателя постоянного тока | Электрические машины
Страница 50 из 51
Основной характеристикой двигателя постоянного тока, определяющей его свойства в установившемся режиме, является механическая характеристика
при и .
Уравнение механической характеристики получается из (6.7)
. (6.8)
На рис. 6.42 представлены механические характеристики при различных способах возбуждения. Механическая характеристика двигателя параллельного возбуждения при небольшой размагничивающей реакции якоря () имеет слабо падающий характер (кривая 1).
Если размагничивающая реакция двигателя параллельного возбуждения велика (поток Ф существенно снижается при увеличении нагрузки), то механическая характеристика будет иметь положительный наклон (кривая 1′). Такая характеристика, как правило, не позволяет получить установившийся режим.
Действительно, запишем уравнение моментов в малых приращениях
.
Решение этого уравнения
,
где С — постоянная, определяемая начальными условиями; — разность частных производных электромагнитного и внешнего моментов.
Решение будет устойчивым ( при ), если , т.е. .
Для постоянной нагрузки характеристика 1′ не удовлетворяет этому условию.
В двигателях последовательного возбуждения результирующий поток пропорционален току якоря,
,
а электромагнитный момент пропорционален квадрату тока якоря,
.
С учетом этих соотношений уравнение механической характеристики двигателя последовательного возбуждения приобретает вид
. (6.9)
Этому уравнению соответствует кривая 2 (рис. 6.42), имеющая гиперболический характер. При частота вращения якоря , поэтому двигатели последовательного возбуждения не могут работать в режиме холостого хода.
Вместе с тем квадратичная зависимость электромагнитного момента от тока якоря дает важное преимущество двигателям последовательного возбуждения при перегрузках перед двигателями параллельного возбуждения, момент которых является линейной функцией тока . Это преимущество особенно существенно при пуске, так как при одном и том же пусковом токе () двигатели последовательного возбуждения развивают больший момент, чем двигатели параллельного возбуждения.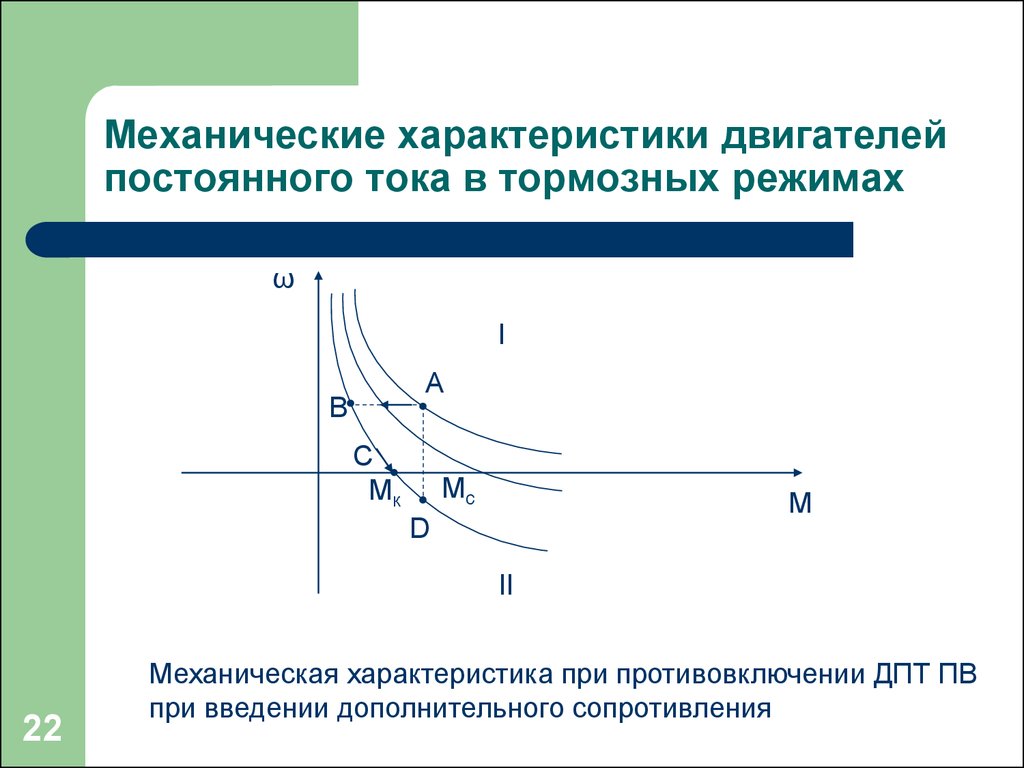 Поэтому двигатели последовательного возбуждения получили широкое применение на транспортных установках, где пусковой режим является одним из основных режимов работы.
Поэтому двигатели последовательного возбуждения получили широкое применение на транспортных установках, где пусковой режим является одним из основных режимов работы.
Механическая характеристика двигателя смешанного возбуждения (кривая 3 рис. 6.42) занимает промежуточное положение. Обладая близкими с двигателями последовательного возбуждения свойствами при перегрузках, двигатели смешанного возбуждения могут работать и при малых нагрузках, что позволяет осуществить рекуперацию энергии в сеть при (рис. 6.42), так как машина переходит в генераторный режим (). Это свойство можно использовать в транспортных установках при движении с горы, создавая тормозной момент и одновременно возвращая в сеть запасенную кинетическую энергию.
- Назад
- Вперёд
3.4. Механические характеристики двигателя постоянного тока последовательного возбуждения
Для
электродвигателя последовательного
возбуждения, принципиальная схема
включения которого представлена
на рис.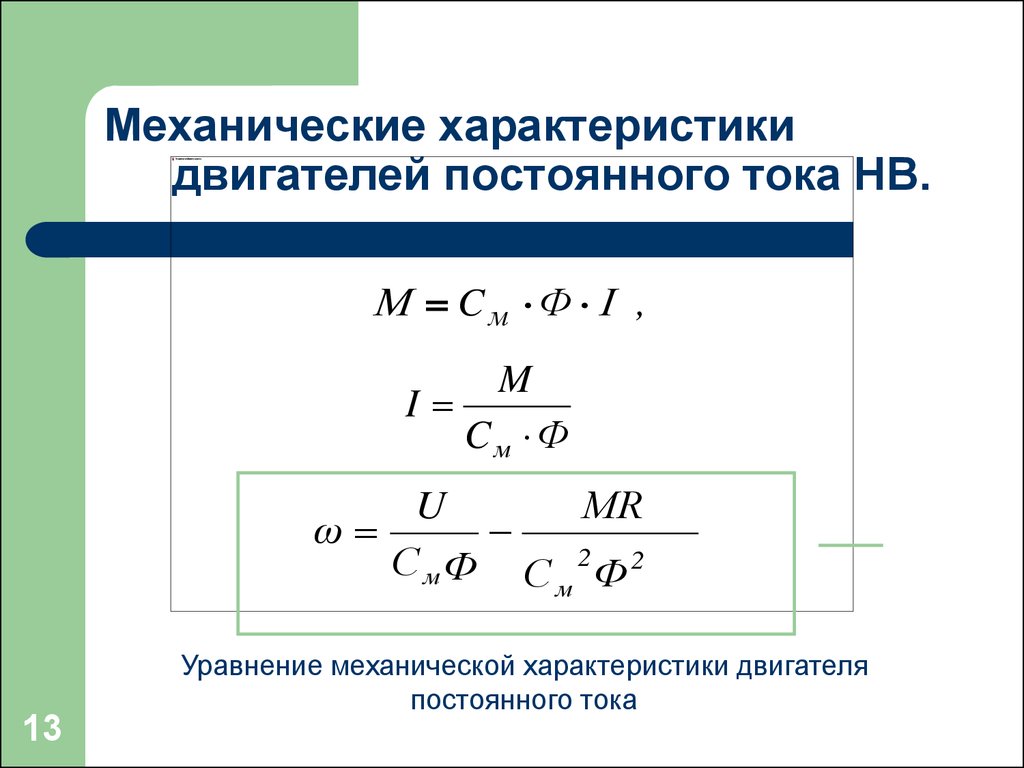 3.10, уравнение электромеханической
3.10, уравнение электромеханической
характеристики,
так же как и для двигателя независимого
возбуждения,
имеет вид:
ω
= (U-
IR)/kФ,
где
R
—
суммарное сопротивление якорной цепи,
состоящее из
сопротивления обмотки якоря, обмотки
возбуждения и сопротивления
внешнего резистора 1.
В
отличие от двигателя независимого
возбуждения здесь
магнитный поток Ф является функцией
тока якоря I.
Эта
зависимость, приведенная на рис. 3.11,
носит название кривой
намагничивания. Так как нет точного
аналитического
выражения для кривой намагничивания,
то трудно дать
и точное аналитическое выражение для
механической характеристики
двигателя последовательного возбуждения.
Если
для упрощения анализа предположить,
пренебрегая
насыщением магнитной системы, линейную
зависимость между
потоком и током якоря, как это показано
пунктиром
1
При наличии дополнительных полюсов
учитывается и их сопротивление.
на
рис. 3.11, т. е. считать Ф =
αI,
то момент двигателя
M
= kФI = αkI2.
(3.28)
Подставив в
равенство для угловой скорости двигателя
значение тока из (3.28), получим выражение
для механической характеристики:
(3.29)
Отсюда следует,
что при ненасыщенной магнитной цепи
двигателя механическая характеристика
изображается кривой (рис. 3.12), для которой
ось ординат является асимптотой.
Особенностью механической характеристики
Рис.
3.10, Схема включения двигателя
постоянного тока последовательного
возбуждения.
Рис.
3.11. Кривая намагничивания
двигателя постоянного тока
последовательного возбуждения.
двигателя
последовательного возбуждения является
ее большая крутизна в области малых
значений момента.
Значительное
увеличение угловой скорости при малых
нагрузках обусловливается соответствующим
уменьшением магнитного потока.
Уравнение
(3.29) дает лишь общее представление о
механической характеристике двигателя
последовательного возбуждения. При
расчетах этим уравнением пользоваться
нельзя, так как машин с ненасыщенной
магнитной системой обычно в современной
практике не строят. Вследствие того,
что действительные механические
характеристики сильно отличаются от
кривой, выраженной уравнением (3.29),
построение характеристик приходится
вести графо-аналити-ческими способами.
Обычно построение искусственных
характеристик производится на основании
данных каталогов, где приводятся
естественные характеристики:
n
= f (I)
и
М
= ψ (I).
Для
серии двигателей определенного типа
эти характеристики
могут быть даны в относительных единицах:
ω*
= f(I*)
и
M*
= ψ(I*).
Такие характеристики, называемые
универсальными, представлены на рис.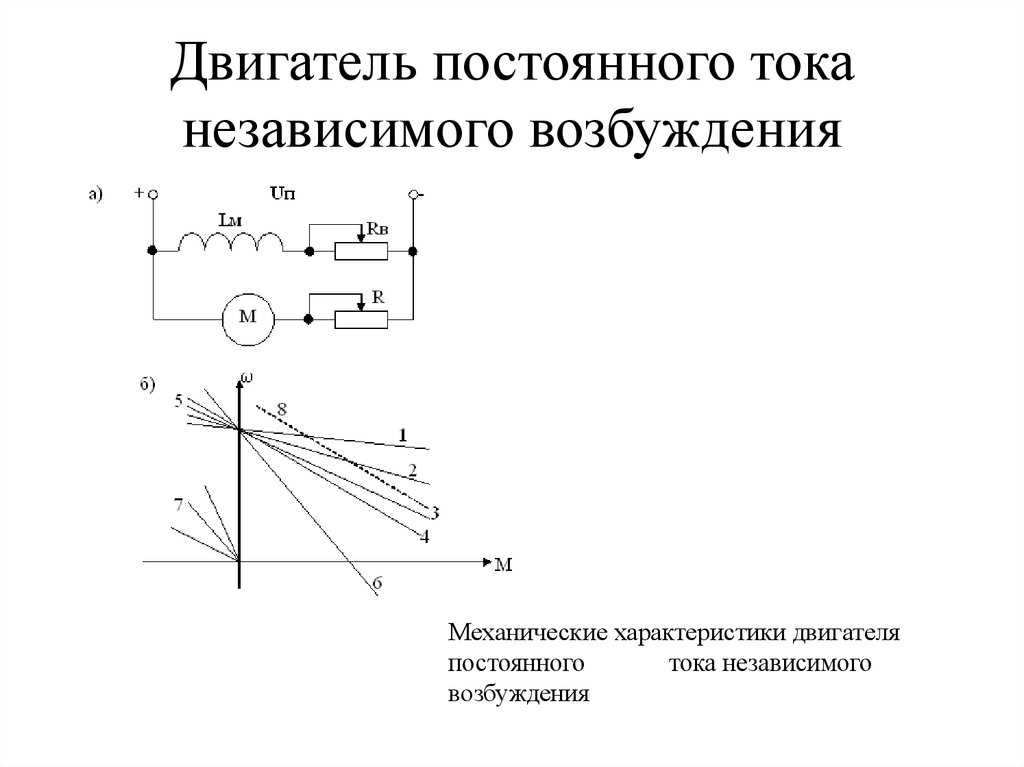
3.13.
Отметим,
что в каталогах дается зависимость
момента на
валу двигателя от тока. При построении
механических характеристик
принимается зависимость угловой скорости
от
электромагнитного момента. Это практически
допустимо
Рис.
3.12. Естественная механическая
характеристика двигателя
постоянного тока последовательного
возбуждения.
Рис.
3.13, Зависимость момента и угловой
скорости от тока якоря двигателя
постоянного тока после довательного
возбуждения (в относительных
единицах).
ввиду
небольшой разницы между электромагнитным
моментом
и моментом на валу.
Для
построения искусственных (реостатных)
характеристик
можно воспользоваться следующим
методом.
Уравнение
естественной характеристики
ωe
= (U
–
IRД)/kФ
,
где
RД
= RВ
+ ЯЯ,
или
(3. 30)
30)
В
случае включения в якорную цепь
дополнительного резистора
Rp
двигатель
будет работать на реостатной
характеристике,
для которой
(3.31)
При делении (3.31)
на (3.30) получим:
ω
/
ωе
= [U
— I (Rд
+ RP)]/(U-
Rд),
отсюда
(3.32)
или в относительных
единицах
(3.33)
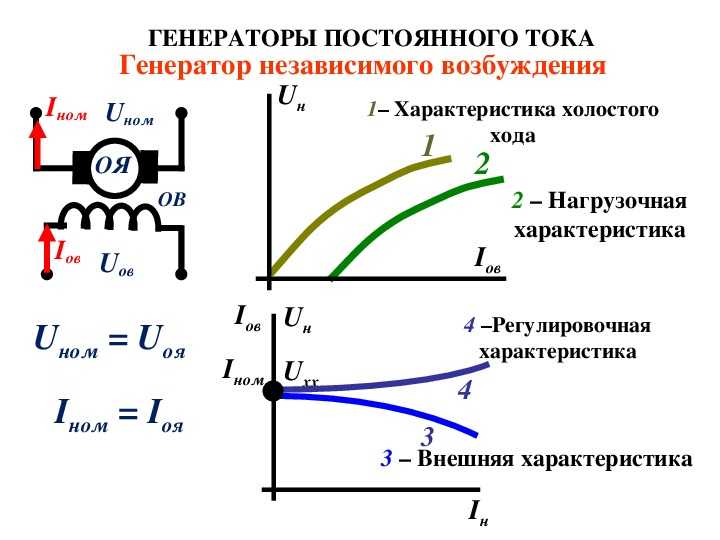
здесь
R*
= (RД
+ RP)
/Rном
— суммарное сопротивление якорной
цепи в относительных единицах;
Rд*
= Rд
/Rном;
ω*
= ω/ωном;
ωe*
= ωe/ωном;
I*
= I/ I ном
.
Порядок
построения реостатной характеристики
сводится
к тому, что, задаваясь некоторыми
произвольными
Рис.
3.14. Естественная и реостатная
электромеханические характеристики
двигателя постоянного тока
последовательного возбуждения (в
относительных
единицах).
Рис.
3.15. Естественная и реостатные
механические характеристики
двигателя постоянного тока
последовательного возбуждения (в
относительных единицах).
значениями
тока I1*,
пo
имеющейся естественной характеристике
находят ωe1*
.
Затем по (3.33) при определенном R*
=
R1*
(для
которого строится реостатная
характери-сдика)
и том же I1*
определяют
искомое значение ω1*.
Таким
же образом для других значений I*
определяют искомые
значения скорости ω2*,
ω2*
и
т. д.
д.
На рис. 3.14 показаны
естественная характеристика двигателя
последовательного
возбуждения RД*
и
реостатная R1*,
построенные
по указанному методу.
Пользуясь
кривой ω*
= f(I*)
(см. рис. 3.13) и электромеханическими
характеристиками, легко построить
кривые
ω*
= f
(М*),
т.
е. механические характеристики двигателя.
На
рис. 3.15 приведены естественная RД*
и
реостатные R1*
–
R3*
механические характеристики двигателя
последовательного
возбуждения, построенные в относительных
единицах.
С увеличением сопротивления скорость
двигателя
при том же моменте уменьшается и
характеристика смещается
вниз. Жесткость характеристики уменьшается
с
ростом дополнительного сопротивления
в якорной цепи.
Рис.
3.16. Графическое построение ступеней
пускового резистора двигателей
постоянного тока последовательного
возбуждения.
Особенностью
механических характеристик рассматриваемого
двигателя является невозможность
получения режима идеального
холостого хода.
При
нагрузке ниже 15—20 % номинальной работа
двигателя
практически недопустима из-за чрезмерного
увеличения
скорости якоря.
Расчет
сопротивлений резисторов для пуска
двигателей последовательного
возбуждения может быть произведен
следующим
графо-аналитическим методом, не требующим
построения
самих реостатных характеристик двигателя.
Воспользуемся
естественной характеристикой двигателя
ω
= f(I)
и, отметив на ней точки допустимых токов
при переключении
с одной ступени резистора на другую I1
и I2
(рис.
3.16), проведем через эти точки пунктиром
две параллельные
линии до пересечения с вертикалью Af
в
точках f
и
е. Вертикаль
Вертикаль
Af
расположена
влево от начала координат
на
расстоянии О
А, соответствующем
внутреннему сопротивлению
двигателя. Откладываем в том же масштабе
отрезки Оа
= R1
= U/I1
и
Og
= R2
= U/I2.
Соединяя точки а
и
е,
а
также
g
и
f,
получаем две прямые, характеризующие
линейную
зависимость между скоростью двигателя
и сопротивлением его якорной цепи
при неизменном токе якоря. Последнее
вытекает из выражения
ω
= (U
— IR)/kФ
= A—BR.
Для
определения числа пусковых ступеней и
их сопротивлений
поступают следующим образом. Проводят
вертикаль через точку а
до пересечения с gf
в
точке b.
Затем
через точку
b
проводят
линию, параллельную оси абсцисс, до
точки
с
на
линии ае.
Аналогично
проводятся линии cd
и
de.
Построение
считается удачным, если последняя
горизонталь проходит
через точку е.
Если
этого не произойдет, то построение
следует повторить, изменив наклон одной
из прямых ае
или
gf
за
счет выбора новых значений
I1
и I2
(чаще изменяют
только I2).
На
рис. 3.16 дано построение с числом ступеней
реостата,
равным двум. Из построения ясно, что
отрезок bc
соответствует
сопротивлению первой ступени реостата,
a
de
—
второй. В момент пуска (при ω
= 0) ток в якоре будет
равен I1,
а сопротивление всей якорной цепи R1
=
=
U/I1.
При
разгоне двигателя до скорости ω1
ток уменьшается,
а сопротивление якорной цепи не
изменяется.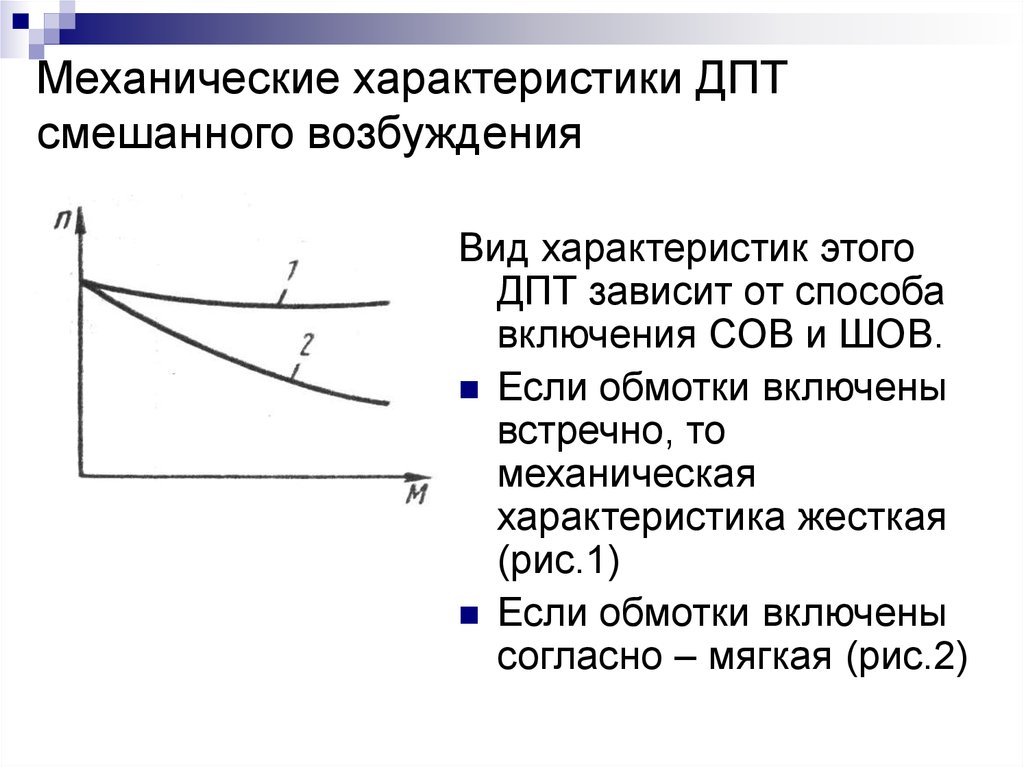 В
В
точке b
сопротивление
то же, но ток равен I2.
Затем при ω
= ω1
происходит шунтирование первой ступени,
общее сопротивление
якорной цепи становится соответствующим
отрезку cc1
а
ток вновь достигает значения I1
и т. д., пока двигатель
не начнет работать на естественной
характеристике.
Характеристики двигателей постоянного тока | www.electriceasy.com
Как правило, для двигателей постоянного тока важными считаются три характеристические кривые: (i) крутящий момент в зависимости от тока якоря, (ii) скорость в зависимости от тока якоря и (iii) скорость в зависимости от крутящего момента. Они объясняются ниже для каждого типа двигателя постоянного тока. Эти характеристики определяются с учетом следующих двух соотношений.
T a ∝ ɸ.I a и N ∝ E b /ɸ
Эти вышеприведенные уравнения могут быть изучены при — ЭДС и уравнении крутящего момента машины постоянного тока. Для двигателя постоянного тока величина противо-ЭДС определяется тем же уравнением ЭДС генератора постоянного тока, то есть E б = PɸNZ / 60А. Для машины P, Z и A постоянны, поэтому N ∝ E b /ɸ
Для двигателя постоянного тока величина противо-ЭДС определяется тем же уравнением ЭДС генератора постоянного тока, то есть E б = PɸNZ / 60А. Для машины P, Z и A постоянны, поэтому N ∝ E b /ɸ
Характеристики двигателей постоянного тока серии
Крутящий момент в зависимости от тока якоря (T
a -I a )
Эта характеристика также известна как электрическая характеристика . Мы знаем, что крутящий момент прямо пропорционален произведению тока якоря на магнитный поток, T a ∝ ɸ.I a . В двигателях постоянного тока обмотка возбуждения включена последовательно с якорем, т.е. I a = I f . Поэтому до магнитного насыщения поля поток ɸ прямо пропорционален Ia. Следовательно, до магнитного насыщения Ta α Ia 2 . Следовательно, кривая Ta-Ia является параболой для меньших значений Ia.
После магнитного насыщения полюсов поля поток ɸ не зависит от тока якоря Ia. Следовательно, крутящий момент изменяется пропорционально только Ia, T ∝ Ia. Поэтому после магнитного насыщения кривая Ta-Ia становится прямой линией.
Следовательно, крутящий момент изменяется пропорционально только Ia, T ∝ Ia. Поэтому после магнитного насыщения кривая Ta-Ia становится прямой линией.
Крутящий момент на валу (Тш) меньше момента якоря (Та) из-за паразитных потерь. Следовательно, кривая Tsh vs Ia лежит несколько ниже.
В двигателях постоянного тока (до магнитного насыщения) крутящий момент увеличивается пропорционально квадрату тока якоря. Эти двигатели используются там, где требуется высокий пусковой крутящий момент.
Скорость в зависимости от тока якоря (N-Ia)
Мы знаем соотношение N ∝ E b /ɸ
При малом токе нагрузки (и, следовательно, при малом токе якоря) изменение противоЭДС Eb мало и им можно пренебречь. Следовательно, для малых течений скорость обратно пропорциональна ɸ. Как известно, поток прямо пропорционален Ia, скорость обратно пропорциональна Ia. Поэтому, когда ток якоря очень мал, скорость становится опасно высокой. это почему нельзя запускать серийный двигатель без механической нагрузки .
Но при больших нагрузках ток якоря Ia велик. И, следовательно, скорость низкая, что приводит к уменьшению обратной ЭДС Eb. Из-за уменьшения Eb допускается больший ток якоря.
Скорость в зависимости от крутящего момента (N-Ta)
Эта характеристика также называется механической характеристикой . Из приведенных выше двух характеристик двигателя постоянного тока серии можно обнаружить, что при высокой скорости крутящий момент низкий, и наоборот.
Характеристики параллельных двигателей постоянного тока
Крутящий момент в зависимости от тока якоря (Ta-Ia)
В случае шунтирующих двигателей постоянного тока можно считать, что поток поля ɸ является постоянным. Хотя при больших нагрузках ɸ несколько уменьшается из-за повышенной реакции якоря. Поскольку мы пренебрегаем изменением потока ɸ, мы можем сказать, что крутящий момент пропорционален току якоря.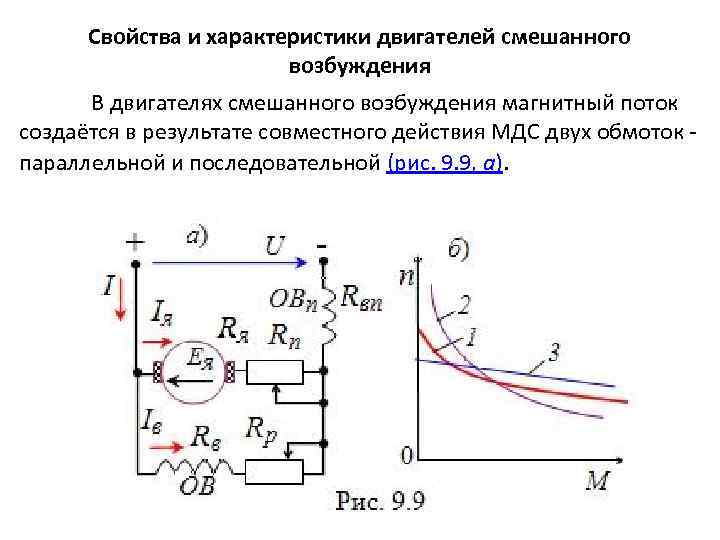 Следовательно, характеристика Ta-Ia для шунтового двигателя постоянного тока будет прямой линией, проходящей через начало координат.
Следовательно, характеристика Ta-Ia для шунтового двигателя постоянного тока будет прямой линией, проходящей через начало координат.
Поскольку при большой пусковой нагрузке требуется большой пусковой ток, 9Шунтирующий двигатель 0029 никогда не должен запускаться при большой нагрузке .
Скорость в зависимости от тока якоря (N-Ia)
Поскольку поток ɸ считается постоянным, мы можем сказать, что N ∝ Eb. Но, поскольку противо-ЭДС также почти постоянна, скорость должна оставаться постоянной. Но на практике ɸ, как и Eb, уменьшается с увеличением нагрузки. Противоэдс Eb уменьшается несколько больше, чем ɸ, следовательно, скорость уменьшается незначительно. Как правило, скорость снижается только на 5–15% от скорости полной нагрузки. Таким образом, параллельный двигатель можно принять за двигатель с постоянной скоростью 9.0009 . В зависимости скорости от тока якоря на следующем рисунке прямая горизонтальная линия представляет идеальную характеристику, а фактическая характеристика показана пунктирной линией.
Характеристики составного двигателя постоянного тока
Составные двигатели постоянного тока имеют как последовательную, так и шунтирующую обмотку. В составном двигателе, если последовательная и шунтирующая обмотки соединены так, что последовательный поток имеет направление, соответствующее направлению шунтирующего потока, то двигатель называется кумулятивно составным. А если последовательный поток противоположен направлению шунтирующего потока, то говорят, что двигатель имеет дифференциальную составляющую. Характеристики обоих составных двигателей поясняются ниже.
(a) Комбинированный накопительный двигатель
Накопительный составной двигатель используется там, где требуются последовательные характеристики, но при этом нагрузка может быть полностью снята. Последовательная обмотка обеспечивает большую нагрузку, в то время как шунтирующая обмотка предотвращает работу двигателя на опасно высоких скоростях при внезапном отключении нагрузки.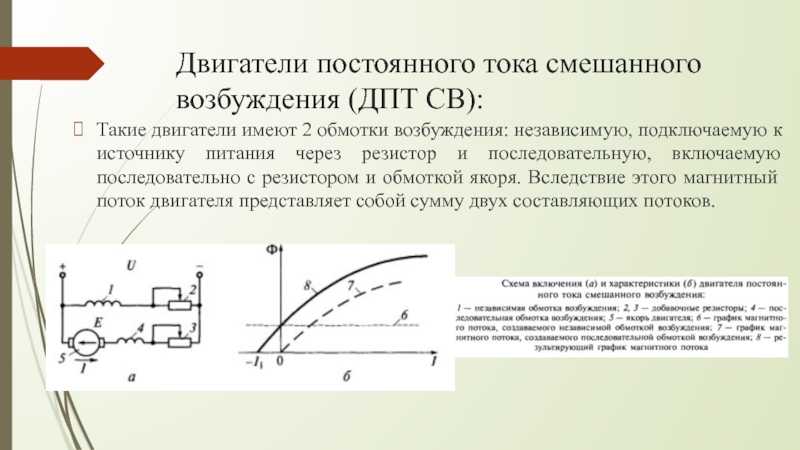 В этих двигателях обычно используется маховик, к которому применяются внезапные и временные нагрузки, как в прокатных станах.
В этих двигателях обычно используется маховик, к которому применяются внезапные и временные нагрузки, как в прокатных станах.
(b) Дифференциальный составной двигатель
Поскольку в двигателях дифференциального возбуждения последовательный поток противодействует шунтирующему потоку, общий поток уменьшается с увеличением нагрузки. За счет этого скорость остается почти постоянной или даже может незначительно возрастать с увеличением нагрузки (N ∝ E b /ɸ). Дифференциальные составные двигатели обычно не используются, но они находят ограниченное применение в экспериментальных и исследовательских работах.
Характеристики двигателя постоянного тока
Производительность и поведение двигателя постоянного тока определяются его характеристиками. Он выражает отношение между двумя или более величинами. Важными характеристиками двигателя постоянного тока являются
- Крутящий момент — характеристики тока якоря (T/Ia) — также называются электрическими характеристиками.
 Он дает зависимость между моментом, развиваемым в якоре, и током, протекающим через якорь.
Он дает зависимость между моментом, развиваемым в якоре, и током, протекающим через якорь. - Скорость — характеристика тока якоря (N/Ia) — также называется характеристикой скорости, которая дает соотношение между током якоря и скоростью вращения двигателя.
- Крутящий момент – характеристики скорости (N/T) – определяет соотношение между крутящим моментом и скоростью двигателя, поэтому называется механическими характеристиками.
Характеристики двигателя постоянного тока
Крутящий момент – характеристики тока якоря
Поскольку обмотка возбуждения соединена последовательно с обмоткой якоря ( φ α I a ), увеличение потока возбуждения приведет к увеличению тока якоря .
Уравнение крутящего момента для двигателя постоянного тока имеет вид T α φI a
При малой нагрузке ток якоря будет меньше, поэтому создаваемый поток будет пропорционален току якоря ( φ α I a ).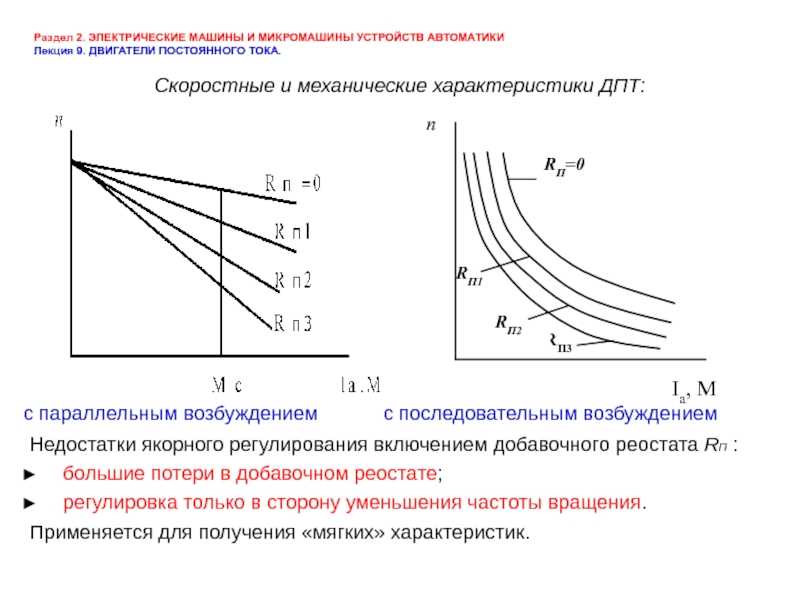 Следовательно, крутящий момент увеличивается пропорционально квадрату тока ( T α I a2 ). Это соотношение дает параболическую кривую до точки насыщения.
Следовательно, крутящий момент увеличивается пропорционально квадрату тока ( T α I a2 ). Это соотношение дает параболическую кривую до точки насыщения.
После насыщения магнитный поток не зависит от тока якоря. С этого момента момент времени будет пропорционален току якоря ( T α I a ). Теперь полученная кривая будет прямой линией. Это показано на рисунке ниже.
Крутящий момент вала или полезный крутящий момент (красная пунктирная линия) будет меньше, чем крутящий момент якоря. Это происходит из-за потерь из-за железа, потерь на трение и ветра.
Из характеристик видно, что крутящий момент двигателя пропорционален квадрату тока до насыщения. Это означает, что двигатель серии постоянного тока имеет высокий пусковой ток.
Следовательно, серийный двигатель используется там, где требуется высокий пусковой момент, например, в подъемниках, электротяге, тележках и т. д. /φ ), ясно, что скорость пропорциональна противо-ЭДС и обратно пропорциональна потоку.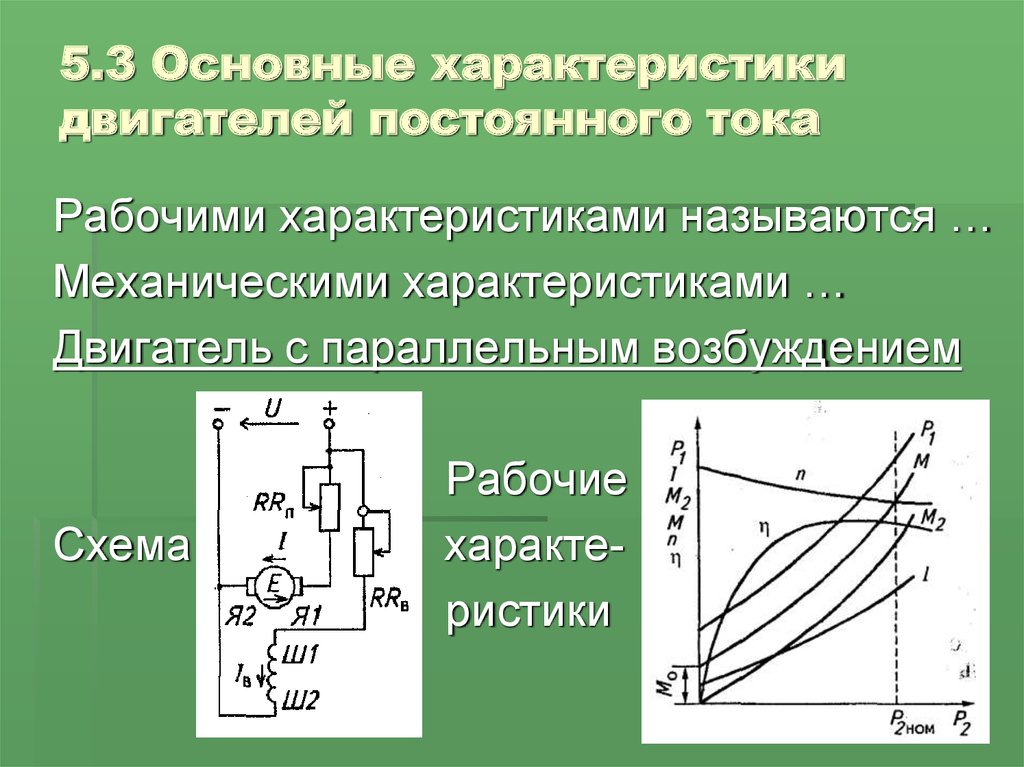
С увеличением тока якоря увеличивается падение напряжения из-за сопротивления якоря и последовательного возбуждения ( E b = V – I a (R a + R se )). Следовательно, противо-ЭДС уменьшается. Так как падение очень мало, им можно пренебречь. Таким образом, скорость обратно пропорциональна потоку.
Когда на двигатель воздействует большая нагрузка, ток якоря будет высоким, что увеличит магнитный поток. Это приведет к уменьшению скорости двигателя. Когда нагрузка уменьшается или нагрузка не подается, поток будет меньше, но скорость будет опасно высокой.
Следовательно, серийный двигатель нельзя запускать без механической нагрузки. Если двигатель запускается без нагрузки, двигатель выходит из строя из-за высокой центробежной силы, создаваемой при скорости вращения.
Крутящий момент – характеристики скорости
Он находится между крутящим моментом и скоростью вращения двигателя постоянного тока.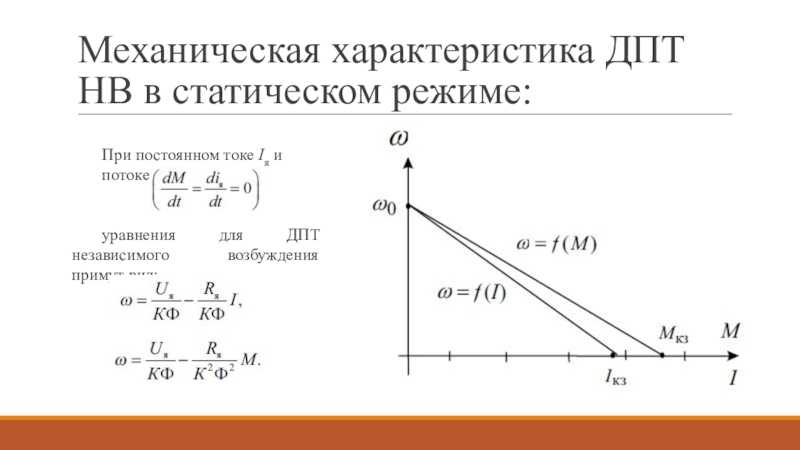 Полученная кривая ясно показывает, что скорость падает при увеличении момента нагрузки. При более высоких нагрузках скорость падает линейно.
Полученная кривая ясно показывает, что скорость падает при увеличении момента нагрузки. При более высоких нагрузках скорость падает линейно.
Следовательно, серийные двигатели используются в приложениях, где двигатель напрямую подключен к нагрузке.
Характеристики шунтового двигателя постоянного тока
Крутящий момент – характеристики тока якоря
Уравнение крутящего момента шунтового двигателя постоянного тока имеет вид T α φI a . Поскольку в случае шунтового двигателя постоянного тока поток на полюс считается постоянным. Следовательно, крутящий момент пропорционален току якоря.
С увеличением тока нагрузки якоря увеличивается крутящий момент, что дает линейную зависимость. Полученная характеристика представляет собой прямую линию, проходящую через начало координат О.
Характеристики скорости тока якоря
Для параллельного двигателя поток считается постоянным. Следовательно, уравнение скорости принимает вид N α E b .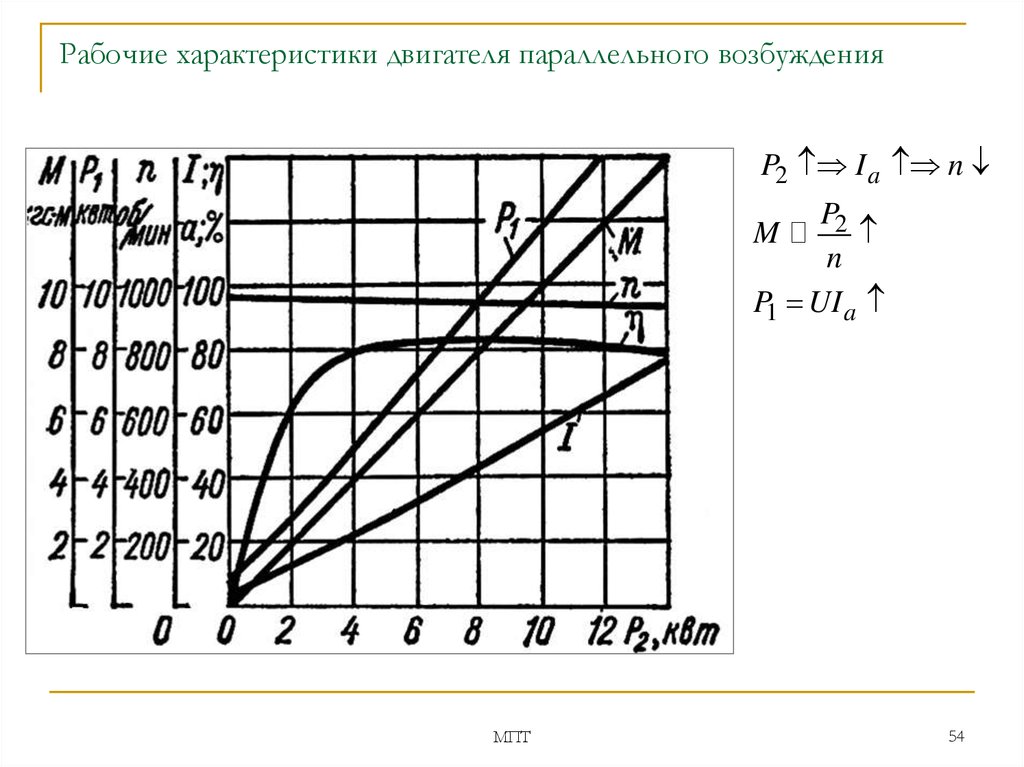 Практически E b постоянна, поэтому скорость также постоянна.
Практически E b постоянна, поэтому скорость также постоянна.
Однако, когда ток нагрузки увеличивается, противо-ЭДС и поток на полюс уменьшаются. Для сравнения, обратная ЭДС уменьшается больше, чем поток, и, следовательно, будет небольшое падение скорости, как показано ниже.
Обычно шунтирующий двигатель называется двигателем с постоянной скоростью, так как нет заметного изменения скорости двигателя от холостого хода до полной нагрузки.
Шунтовой двигатель постоянного тока благодаря своим характеристикам используется в таких устройствах, как обрабатывающие инструменты, токарные станки, деревообрабатывающие станки и т. д. из двух вышеперечисленных характеристик.
Характеристики комбинированного двигателя постоянного тока
Составные двигатели имеют как последовательную обмотку возбуждения, так и шунтирующую обмотку возбуждения. По возбуждению они бывают двух типов: кумулятивно-составные и дифференциально-составные двигатели.
Составные накопительные двигатели
Если поток последовательного поля помогает потоку шунтирующего поля, то это двигатель с накопительным составом. Такие машины имеют характеристики как серийного двигателя, так и параллельного двигателя.
Такие машины имеют характеристики как серийного двигателя, так и параллельного двигателя.
Они используются в приложениях, где предполагается полное снятие нагрузки. За счет шунтирующих обмоток возбуждения скорость не станет чрезмерно высокой. В то же время последовательные обмотки возбуждения смогут воспринимать большие нагрузки.
Двигатели с накопительным составом используются для приложений с высоким пусковым моментом, таких как краны, лифты и т. д. Также используются для приложений, где важно внезапное приложение и снятие нагрузки.
Дифференциальные составные двигатели
В этой машине поток, создаваемый последовательной обмоткой возбуждения, противодействует потоку, создаваемому параллельной обмоткой возбуждения, и уменьшает его. Следовательно, чистый поток уменьшается с увеличением нагрузки.
В результате скорость двигателя увеличивается( N α E б /φ ). Это приводит к снижению крутящего момента двигателя, что делает дифференциальный составной двигатель непригодным для работы в условиях перегрузки.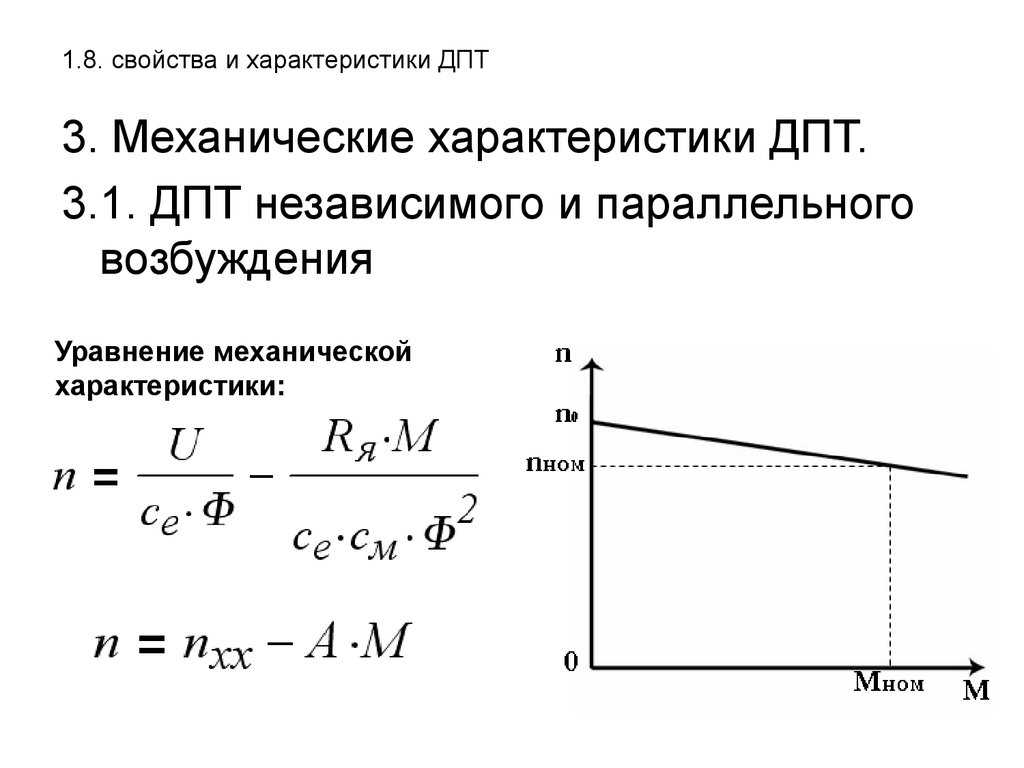
 Он дает зависимость между моментом, развиваемым в якоре, и током, протекающим через якорь.
Он дает зависимость между моментом, развиваемым в якоре, и током, протекающим через якорь.