Содержание
Построение механической характеристики асинхронного двигателя
Асинхронный двигатель
Для оценки свойств асинхронного двигателя прибегают к построению механической характеристики.
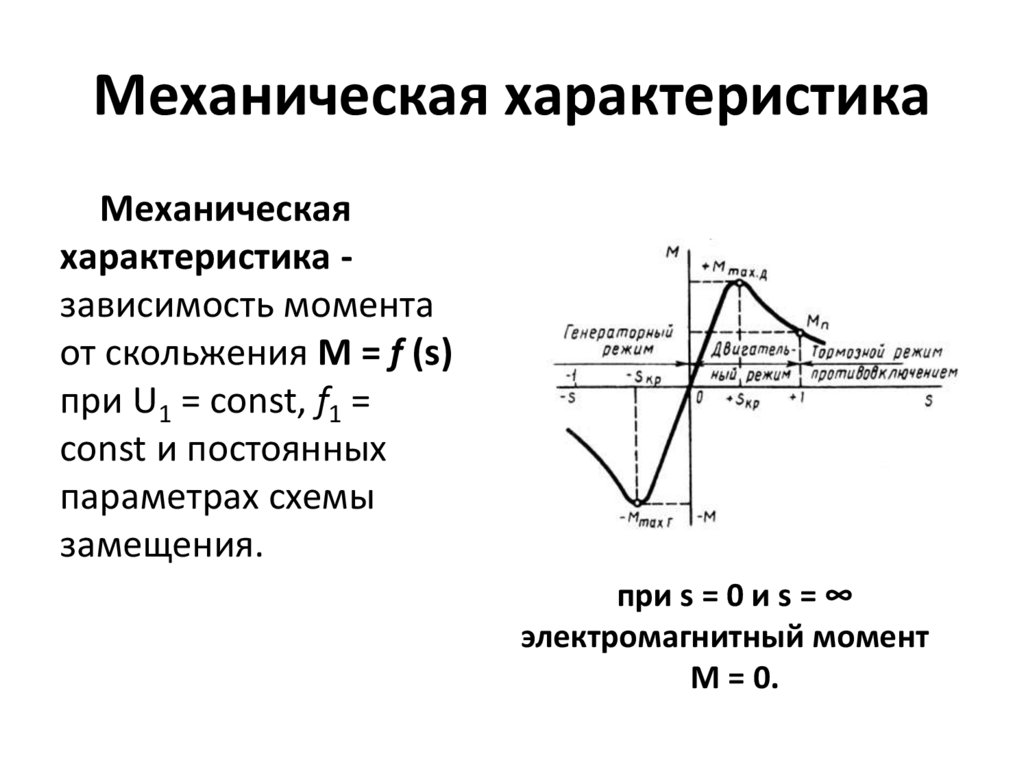
Механическая характеристика асинхронного двигателя выражает зависимость между электромагнитным моментом и частотой вращения, либо скольжением. Скольжение – это величина, которая показывает, насколько частота вращения магнитного поля опережает частоту вращения ротора.
Благодаря механической характеристике, появляется возможность определить к какому типу установки больше подходит двигатель, на каком участке сохраняется его устойчивая работа, перегрузочную способность и другое.
Построим механическую характеристику для двигателя 4A90L4У3.
Паспортные данные двигателя:
n1 = 1500 об/мин
Pн = 2.2 КВт
nн = 1425 об/мин
η = 80 %
cos φ = 0.83
Mmax/Mн = λ = 2,2
Для построения нам необходимо произвести расчет номинального момента и скольжения.
Рассчитаем критическое скольжение и момент, для этого необходимо знать коэффициент λ.
Итак, мы определили основные точки характеристики, но для её построения их недостаточно. Поэтому с помощью упрощенной формулы Клосса, рассчитаем моменты для других значений скольжений.
Упрощенная формула Клосса выглядит следующим образом
Для удобства составим таблицу.
|
s
|
0
| sн | sкр/2 | sкр |
0.2
|
0.3
|
0.4
|
0.5
|
0.6
|
0.
|
0.8
|
0.9
|
1
|
|
M
|
0
|
14.61
|
25.94
|
32.43
|
32,39
|
30.47
|
26.69
|
23.16
|
20.22
|
17.85
|
15.93
|
14.35
|
13.05
|
|
n
|
1500
|
1425
|
1342.
|
1185
|
1200
|
1050
|
900
|
750
|
600
|
450
|
300
|
150
|
0
|
Рассчитаем для каждого значения скольжения момент и частоту вращения. Например, для значения 0.2
Частоту вращения выразим из формулы для определения скольжения
Подобным образом рассчитываются остальные значения.
Так как формула упрощенная, значения могут несколько отличаться от действительных, что не критично для расчетов.
Теперь на основании расчетов мы можем построить саму механическую характеристику.
Зависимость момента от скольжения M = f(s)
Зависимость частоты оборотов от момента n = f(M)
Рекомендуем — механическая характеристика электропривода
3.5.2. Электромеханические и механические характеристики асинхронного двигателя
Электромеханическая
характеристика определяет зависи-мость
между скоростью вращения ротора
(или скольже-
нием) и током
статора I1 или током ротора I’2.
Электромеханические
характеристики асинхронных двигателей
рассчитывают согласно схеме замещения
(рис. 3.29) по формуле
I2(s)
=
, (3.43)
где
I2(s)
– электромеханическая характеристика
двига-теля по току ротора, А.
В режиме идеального
холостого хода через обмотки статора
протекает только ток намагничивания
Iμ, который
создаёт магнитный поток в статоре,
поэтому ток статора определяется
как геометрическая
сумма приведённого тока ротора и намаг-
ничивающего тока
I21
= I‘22
+ I 2µ.
(3.44)
65
Механической
характеристикой асинхронного двигателя
принято называть зависимость
электромагнитного момента М от скольжения,
то есть M = f(s) или = f(M),
вывод которой приведен ниже.
Электромагнитная мощность трёх фаз,
которая передаётся через воздушный
зазор ротору двигателя, равна
Pэм
= 3·I’22·R’2/S
. (3.45)
Эта же мощность
через электромагнитный момент
представляется как
Pэм
= Мэм·ω0,
(3.46)
откуда
Mэм
= Pэм/w0
= 3·I’2·R’2/(ω0·S).
(3.47)
Зависимость (3.47)
с учётом (3.43) представляет собой
механическую
характеристику для двигательного
режима.
(3.48)
Кривая момента М
= f (s) имеет
два максимума:
один — в генераторном
режиме, другой – в двигательном.
Приравнивая dM/ds
= 0, можно определить координаты этих
максимумов. Во первых, определяется
скольжение, при котором момент двигателя
будет максимальным и которое называется
критическим
.
(3.49)
Знак (плюс)
соответствует двигательному режиму, а
знак (минус) – генераторному режиму с
отдачей энергии в сеть. Если подставить
в уравнение (2.47) значение sкр, то
получим выражение критического момента
.
(3. 50)
50)
Из
формулы (3.50) следует, что Мкр в
генераторном режиме будет отрицательным
и по абсолютному значению в 1,5…3 ра-
66
за больше критического
момента в двигательном режиме.
Разделив уравнение
(3.48) на уравнение (3.50), после соответствующих
преобразований получим уравнение
ме-ханической характеристики, применяемое
для двигателей малой мощности
,
(3.51)
где
Мк, Sк –
соответственно критические момент и
скольже-
ние
асинхронного двигателя,
α = R1/R2‘.
Для двигателей
средней и большой мощности, полагая
R1
≈ 0, механическую характеристику
строят по упрощенной формуле, позволяющей
использовать лишь паспортные данные
двигателя
,
(3.52)
Анализируя
характерные точки и области работы АД,
строят
зависимость М = f (s):
1)s
=
0; М
= 0,
при этом скорость двигателя равна
синхронной;
s
= sн;
М
= Мн,
что
соответствует номинальной скорости и
номинальному моменту;s
= sК;
М
= Мк
—
максимальный момент в двигательном
режиме;
4)
s=
1,0; M=Mп–
начальный пусковой
момент;
5) s
= —sк ; М
= -Мкг– максимальный
момент в генера-торном режиме;
6) область
работы при малых скольжениях s
≤ sк, когда можно
пренебречь первым членом в знаменателе
выражения (3.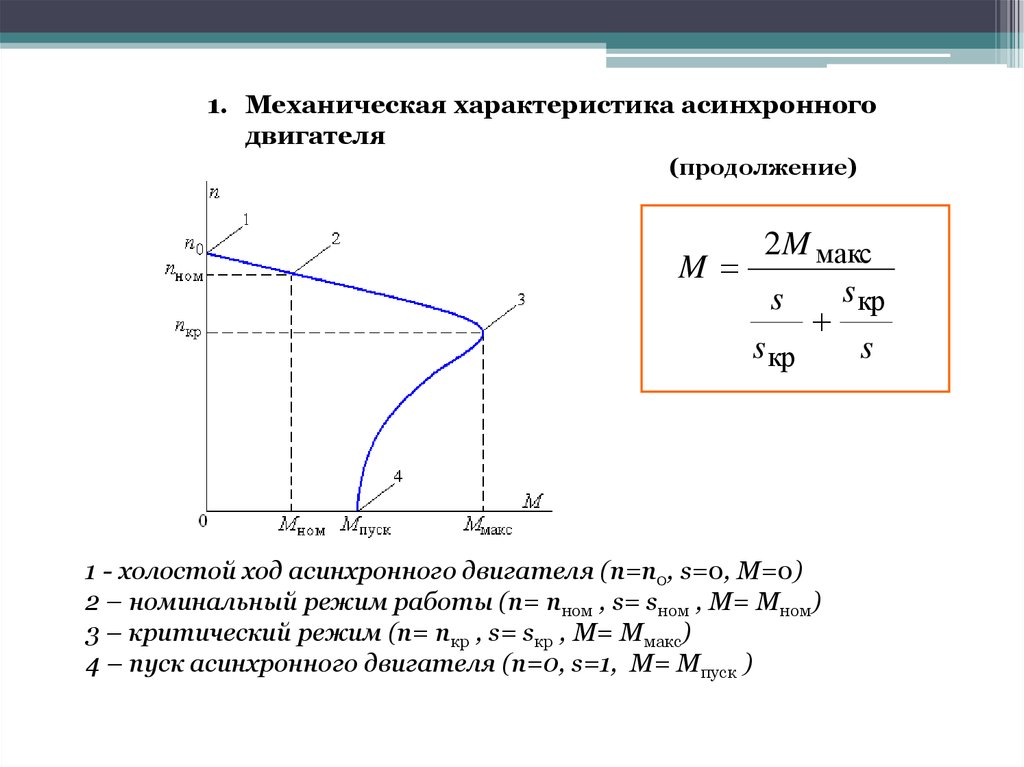 52)
52)
,
67
которое представляет
уравнение прямой;
7) область работы
при больших скольжениях s
≥ sк, когда можно
пренебречь вторым членом в знаменателе
выражения (3.52)
,
которое представляет
уравнение гиперболы.
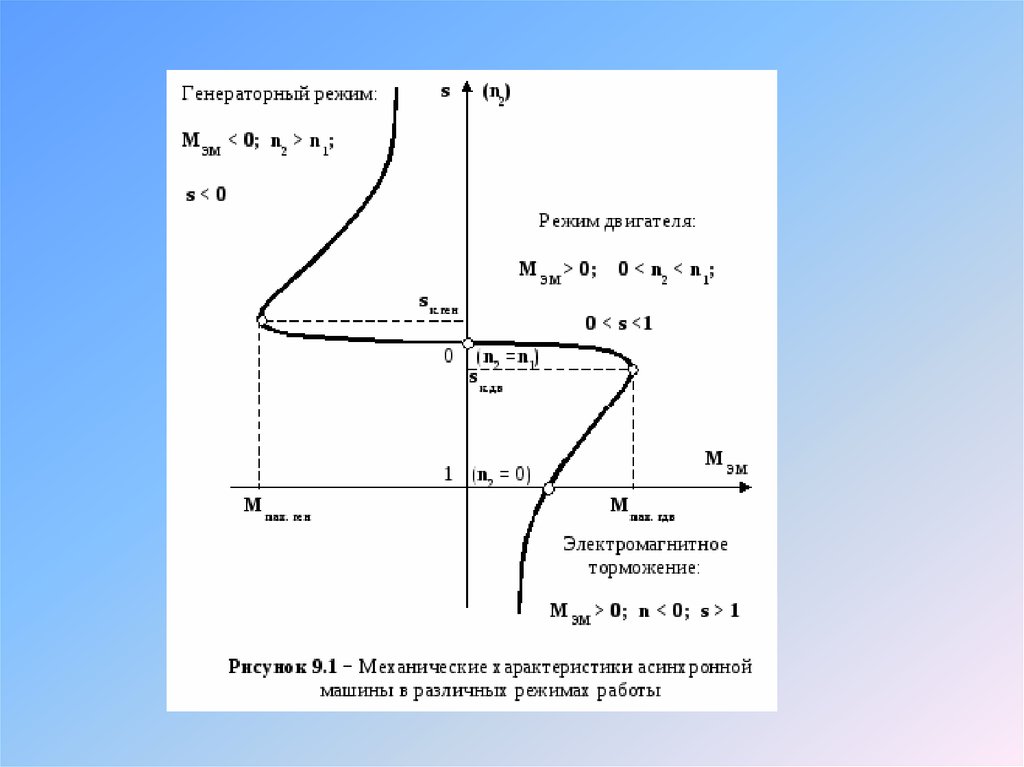
В
соответствии с вышеизложенным можно
изобразить механическую характеристику
АД (рис.3.30). В теории электропривода
начало координат переносят в точку s
= 1 и оси поворачивают на π/2, т.е. делают
зависимость s = f
(M).
Аналогично строится
по характерным точкам и областям в
соответствии с (3. 43) электромеханическая
43) электромеханическая
характеристика (рис.3.31):
Рис.
3.30. Механические характеристики АД
1)
s
= 0, ω = ω0,,
= 0, I1=
I0
— точка идеального хо-лостого
хода;
68
2)
s
= 1, ω = 0, I1
= Iкз=
Iп
—
точка короткого замыкания;
3)
s1=
,
=
Imax=
Uф/xк
— точка
максимального
значения тока ротора, лежащая в области
отрицательных
скольжений;
4)
s
→ ±∞, ω→± ∞,
→I∞
= Uф/
— асимпто-
тическое
значение тока ротора при бесконечно
большом
увеличе-
нии
скольжения и скорости.
И
также, как для механической характеристики,
начало координат переносят в точку s
= 1 и делают зависимость
S =
f (
).
На рис. 3.32 представлены механическая
харак-теристика S = f(M)
и электромезаническая S
= f(
).
Рис.
3.31. Электромеханические характеристики
АД
[№ 36] Некоторые существенные особенности асинхронного двигателя – 1
Рис. 1
В столбце 34 мы вывели несколько свойств, присущих синхронному реактивному двигателю, просто изучив его поперечное сечение и приняв во внимание основные пути потока, и здесь мы сделайте то же самое для асинхронного двигателя, рис. 1. Чтобы стимулировать внимательное изучение чертежа и использовать общепринятую терминологию, рис. 1 представлен без надписей.
Начнем со статора — подождите, что такое «статор»? это stat ionary или stat ic часть, точно так же, как ротор является частью rot ating. На рис. 1 статор находится снаружи, а ротор внутри (но есть несколько экземпляров асинхронных двигателей, в которых ротор находится снаружи, а статор внутри). Ротор и статор по существу имеют цилиндрическую форму и разделены воздушным зазором, который на рис. 1 явно очень мал по сравнению с диаметром ротора.
Посмотрим на статор. Мы можем видеть цветные концевые обмотки, которые соединяют стороны катушки между двумя пазами. Стороны катушки, идущие вдоль пазов, видны только как точки. Имеется 36 пазов, и каждая катушка имеет размах 8 пазов или 8 шагов пазов. Поскольку имеется 36 катушек, каждая с двумя сторонами катушки, в каждом слоте есть 2 стороны катушки, и это называется двухслойной обмоткой. В этом случае одна сторона катушки находится в нижней части прорези, а другая — в верхней части другой прорези.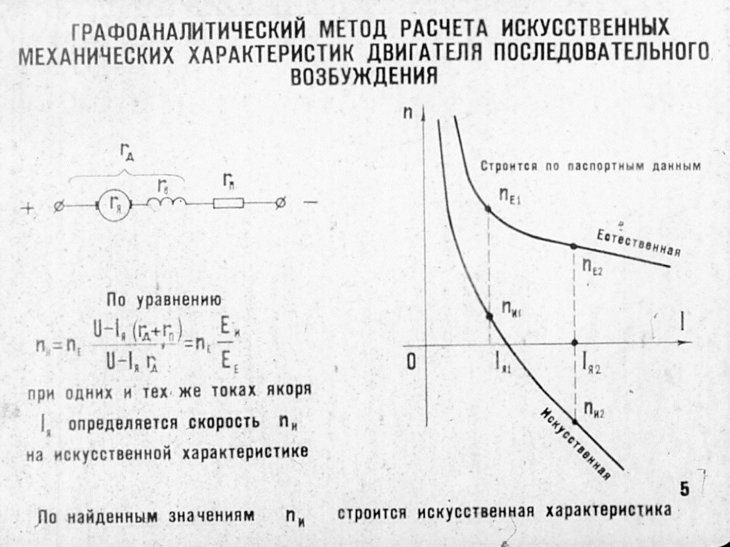 То, как это достигается, является одним из чудес производства электродвигателей. Есть несколько способов, и один из самых элегантных, которые мы видим в настоящее время в автомобильных тяговых двигателях, — это шпильочная обмотка. Поищите в интернете «шпильочная обмотка в электродвигателях», и вы увидите много замечательных примеров.
То, как это достигается, является одним из чудес производства электродвигателей. Есть несколько способов, и один из самых элегантных, которые мы видим в настоящее время в автомобильных тяговых двигателях, — это шпильочная обмотка. Поищите в интернете «шпильочная обмотка в электродвигателях», и вы увидите много замечательных примеров.
Катушки уложены группами по три: красная, красная, красная, затем синяя, синяя, синяя, затем зеленая, зеленая, зеленая; и этот шаблон повторяется четыре раза на 360 °, двигаясь против часовой стрелки. Цвета обозначают три фаз UVW, и если мы назначим U=красный, V=зеленый, W=синий, мы обозначим всю обмотку (в направлении против часовой стрелки):
UUU WWW VVV UUU WWW VVV UUU WWW VVV UUU WWW VVV
Порядок важен! В трехфазной машине пространственный порядок фазных обмоток определяет направление вращения, и если три синусоидальных фазных тока находятся в своей нормальной фазе последовательность UVW во времени, может показаться, что наша последовательность намотки обратная: UWV вместо UVW. Разве порядок не должен быть UVW, идущим против часовой стрелки?
Разве порядок не должен быть UVW, идущим против часовой стрелки?
Чтобы понять это немного лучше, нам нужно посмотреть на количество полюсов.
Количество полюсов в асинхронном двигателе неочевидно. Нет никаких магнитов или обмоток возбуждения, которые нужно считать. Ротор имеет 30 пазов, но количество полюсов точно не 30. И уж точно не 15 (30/2). В любом случае к ротору ничего не подключено, поэтому определить количество полюсов он никак не может. Так что же определяет количество полюсов?
Обмотка статора определяет количество полюсов. Ключевым признаком, на который следует обратить внимание, является количество групп катушек в одной фазе, скажем, в красной фазе U. Катушки уложены группами по три, а групп всего четыре. Это означает четыре полюса .
Если у нас 4 полюса, шаг полюсов равен 360°/4 = 90°. Это точно соответствует 9 слотам. Мы называем это число слотов на полюс . Поскольку это целое число, мы называем статор интегральным слотом 9. 0018 статор.
0018 статор.
Мы уже отметили, что каждая катушка охватывает 8 пазов, а не 9. Мы говорим, что катушки короткошаговые или хордовые . (Катушка, охватывающая 9 слотов, будет катушкой с полным шагом ). Кроме того, три катушки, принадлежащие одной группе, разнесены или распределены под определенным углом, а количество пазов на полюс на фазу равно 9/3 = 3. значение на рис. 1 равно 3 × 360/36 = 30°. Этот угол определяет то, что мы называем фазовый ремень , и мы можем идентифицировать фазовый ремень, посчитав вместе 3 красных стороны катушки в отверстии статора и взяв угол между центральными линиями зубьев с обеих сторон этой группы, то есть 3 шага пазов. или 30°. Важно понимать угол фазового пояса как три шага пазов, а не два (именно так мы могли бы подумать, если мы «прыгаем» с первой красной стороны катушки на третью красную сторону катушки).
Теперь давайте немного подумаем. Вы можете закрыть глаза на этот бит: это может помочь. Давайте зададим себе вопрос: как далеко мы ожидаем, что ротор будет вращаться за один цикл частоты сети переменного тока ? Логичный ответ, конечно, два поула. Это, конечно, означало бы, что все в машине выглядело бы точно так же — все выравнивания, все симметрии, все детали чертежа, а также схема потока и распределение амперпроводников были бы точно воспроизведены после поворота два полюса. И после еще одного поворота двух полюсов, и еще, рисунок будет выглядеть точно так же.
Давайте зададим себе вопрос: как далеко мы ожидаем, что ротор будет вращаться за один цикл частоты сети переменного тока ? Логичный ответ, конечно, два поула. Это, конечно, означало бы, что все в машине выглядело бы точно так же — все выравнивания, все симметрии, все детали чертежа, а также схема потока и распределение амперпроводников были бы точно воспроизведены после поворота два полюса. И после еще одного поворота двух полюсов, и еще, рисунок будет выглядеть точно так же.
Это интуитивное объяснение того, что мы называем синхронной скоростью . Это число циклов в секунду, умноженное на количество пар полюсов — , или ƒ p об/сек, где ƒ — частота, а p — количество пар полюсов. Это скорость, с которой вращается картина потока и распределение амперпроводника. Почему пары полюсов, а не полюса? Полюса идут парами (NS), и полный пространственный цикл охватывает два шага полюса. За один полный цикл частоты переменного тока вращение на синхронной скорости пройдет 360/ p градусов, а полный оборот он покроет за p циклов частоты питания.
Теперь давайте предположим, что мы хотим, чтобы двигатель на рис. 1 вращался против часовой стрелки, и предположим, что последовательность фаз UVW или красный, зеленый, синий. Ток в зеленой фазе V достигнет пикового значения через одну треть цикла во времени после пика в красной фазе U. За одну треть цикла вращение с синхронной скоростью составит 1/3 × 360°/ р , а так 2 p = 4 (определено нашей обмоткой), у нас есть p = 2 и, таким образом, это вращение 120/ p = 60°.
Таким образом, чтобы вращаться против часовой стрелки, мы ожидаем найти зеленую фазу (V), расположенную на 60° вокруг красной фазы (U), идущую против часовой стрелки. В этом месте я попрошу вас, дорогой читатель, изучить рис. 1 и убедиться, что зеленая фаза именно там, где она должна быть. В качестве подсказки начните с любой катушки красной фазы и отсчитайте 60° или 6 шагов щели в направлении против часовой стрелки. Вы должны найти катушку, принадлежащую зеленой фазе, и эта катушка должна находиться в таком же позиционном отношении относительно других катушек зеленой фазы, как красная пусковая катушка была к другим катушкам красной фазы.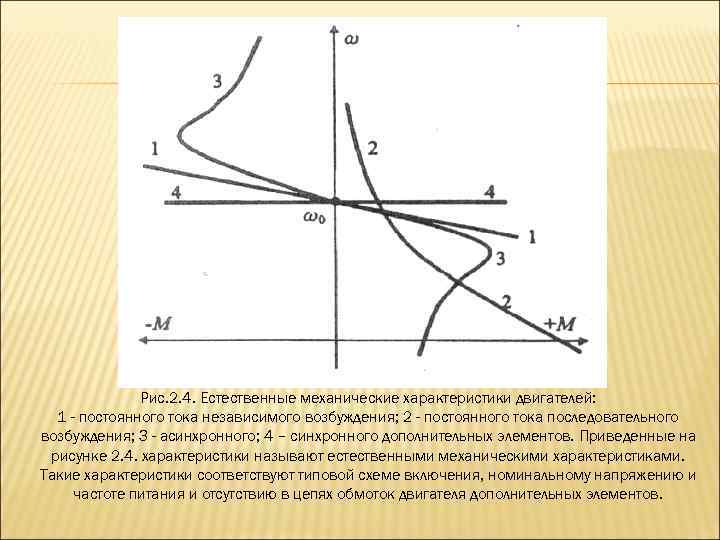
Это важное упражнение. Я бы сказал, что студент должен решить это в своем уме — и, конечно же, дать тот же ответ, что и профессор! Надеюсь, я не ошибся в рисунке. Я уверен, что это нормально. Если нет, мне кто-нибудь напишет (надеюсь). Но за словами может быть сложнее следить, чем за диаграммой. Важно уяснить себе эти основные понятия, и нужно сказать, что многие учебники начинаются с довольно академического или абстрактного уровня, предполагая, что читатель уже имеет эти понятия. Лучше всего посетить обмоточную мастерскую или мастерскую по ремонту обмоток и спросить у техников, как они определяют порядок фаз относительно требуемого направления вращения.
Терминология также важна, чтобы мы могли обсудить все дело друг с другом. Может быть, мне следовало поставить метки на диаграмме, чтобы избежать недоразумений. Если бы я поставил метки, могло бы показаться, что диаграмма не требует пояснений. Но это не так. Как и многие инженерные схемы, она требует интерпретации и воображения со стороны читателя. Надеюсь, я не уклоняюсь от своего долга учителя. Наоборот, хороший учитель обязательно должен ставить упражнения! Легкие? Может быть, а может и нет.
Надеюсь, я не уклоняюсь от своего долга учителя. Наоборот, хороший учитель обязательно должен ставить упражнения! Легкие? Может быть, а может и нет.
В следующий раз мы начнем разбираться в реальной работе асинхронного двигателя. Если подумать, мы до сих пор обсуждали только обмотку, и эта обмотка могла бы работать так же хорошо с синхронным двигателем, таким как IPM или двигатель с возбуждением. В синхронном двигателе ротор вращается синхронно с вращающимся магнитным потоком и распределением амперпроводников с синхронной скоростью. Но не в асинхронном двигателе.
Обратите внимание, что все углы в этой статье даны в механических градусах (не в электрических градусах). Фазовый пояс 30° — это фазовый пояс 60° в электрических градусах, и это будет привычным способом его описания в традиционной теории обмоток.
Ссылки
- Хендершот Дж.Р. и Миллер Т.Дж.Е., Проектирование бесщеточных машин с постоянными магнитами , опубликовано Motor Design Books LLC, ISBN 978-0-9840687-0-8, (822 стр.
 ), 2010. Доступно по адресу [email protected].
), 2010. Доступно по адресу [email protected]. - Хендершот Дж. Р. и Миллер Т. Дж. Э., Проектные исследования электрических машин , будет опубликовано Motor Design Books LLC, 2021 г.
Электрические асинхронные двигатели скольжения
Асинхронный двигатель переменного тока (переменного тока) состоит из статора и ротора, и взаимодействие токов, протекающих в стержнях ротора, и вращающегося магнитного поля в статоре создает крутящий момент, который вращает двигатель . При нормальной работе с нагрузкой скорость ротора всегда отстает от скорости магнитного поля, что позволяет стержням ротора пересекать силовые линии магнитного поля и создавать полезный крутящий момент.
Разница между синхронной скоростью магнитного поля электродвигателя и скоростью вращения вала составляет скольжение — измеряется в об/мин или частоте.
Скольжение увеличивается с увеличением нагрузки, что обеспечивает больший крутящий момент.
Скольжение принято выражать как отношение скорости вращения вала к скорости синхронного магнитного поля.
с = (n с — n а ) 100% / N S (1)
, где
S = Slip
N S
N S
N S 9013
N S 9013 9013 r.
n a = скорость вращения вала (об/мин, об/мин)
Когда ротор не вращается, скольжение составляет 100 % .
Скольжение при полной нагрузке варьируется от менее 1 % в двигателях высокой мощности до более 5-6 % в двигателях младших л.с.
| Motor Size (hp) | 0.5 | 5 | 15 | 50 | 250 |
|---|---|---|---|---|---|
| Typical Slip (%) | 5 | 3 | 2,5 | 1,7 | 0,8 |
Число полюсов, частота и скорость синхронного асинхронного двигателя
| Число магнитных полюсов0183 | Frequency (Hz) | |
|---|---|---|
| 50 | 60 | |
| 2 | 3000 | 3600 |
| 4 | 1500 | 1800 |
| 6 | 1000 | 1200 |
| 8 | 750 | 900 |
| 10 | 600 | 720 |
| 12 | 500 | 600 |
| 16 | 375 | 450 |
| 20 | 300 | 360 |
. по максимуму. Скольжение и ток двигателя уменьшаются, когда ротор начинает вращаться.
по максимуму. Скольжение и ток двигателя уменьшаются, когда ротор начинает вращаться.
Частота скольжения
Частота уменьшается при уменьшении скольжения.
Скольжение и индуктивное сопротивление
Индуктивное сопротивление зависит от частоты и скольжения. Когда ротор не вращается, частота скольжения максимальна, как и индуктивное сопротивление.
У двигателя есть сопротивление и индуктивность, и когда ротор вращается, индуктивное сопротивление низкое, а коэффициент мощности приближается к на .
Скольжение и импеданс ротора
Индуктивное сопротивление будет изменяться при скольжении, поскольку полное сопротивление ротора представляет собой сумму фаз постоянного сопротивления и переменного индуктивного сопротивления.
Когда двигатель начинает вращаться, индуктивное сопротивление высокое, а полное сопротивление в основном индуктивное. Ротор имеет низкий коэффициент запаздывающей мощности. Когда скорость увеличивается, индуктивное сопротивление уменьшается, равное сопротивлению.
 7
7 5
5 ), 2010. Доступно по адресу
), 2010. Доступно по адресу