Замер цилиндров: Замер компрессии в двигателе. Как правильно измерить компрессию.

Содержание

Замер компрессии в двигателе, цена 250 руб за цилиндр. Замерить компрессию в дизельном двигателе.

Специализируемся на ремонте, и обслуживании иномарок

Онлайн

Офлайн

Кузовной калькулятор

Оценить ремонт по фото

Примеры работ

Поиск по сайту

Закрыть

Cтраница обновлена: 23 мая, 14:45

Стоимость услуг по замеру компрессии двигателя

Заявка успешно отправлена!

Когда нужен замер компрессии:

при наличии проблем с запуском двигателя;

в случае снижения мощности двигателя;

при увеличении расхода масла;

в случае очевидной неисправности одного из цилиндров, проявляющейся «цоканьем» двигателя;

перед покупкой подержанного автомобиля.

Зачем нужно измерять компрессию двигателя:

для выявления текущего состояния цилиндропоршневой группы механизмов;

для поиска причин неисправностей двигателя;

для выявления вышедшего из строя цилиндра.

Зачем проводится диагностика силовой установки

в профилактических целях;

для выявления неисправностей.

Компрессия двигателя зависит от:

способа размещения манометра в диагностическом оборудовании;

правильности установки углов зажигания;

состояния поршневых колец;

степени прилегания тарелки клапана к седлу.

При закрытом дросселе можно определить следующие дефекты:

плохое прилегание клапана к седлу;

зависание клапана;

недостатки сечения кулачка распределительного вала;

негерметичность, возникшую в результате прогара прокладки ГБЦ или появления щелей в стенке камеры сгорания.

Нормальные значения давления в этом случае равняются 0,6-0,8 МПа.

Измерение компрессии может проводиться как на горячем двигателе, так и на холодном (в случае наличия затруднений с запуском силовой установки). Типичные значения давления обычно имеются в сопровождающей технической документации по обслуживанию автомобиля. Полученные в результате измерений цифры сравниваются с ними и между собой. На основании полученных результатов впоследствии делаются соответствующие выводы.

Очевидно, что процесс замера давления силовой установки хоть и достаточно прост сам по себе, тем не менее, имеет свои особенности. Так, например, для того, чтобы сделать правильный вывод о состоянии двигателя, необходимо не только безукоризненно произвести все измерительные манипуляции, но и принять во внимание динамику нарастания давления и множество других не менее важных деталей, а также верно интерпретировать полученные значения. Именно поэтому при возникновении необходимости в таком обслуживании мы настоятельно рекомендуем пользоваться услугами профессиональных специалистов.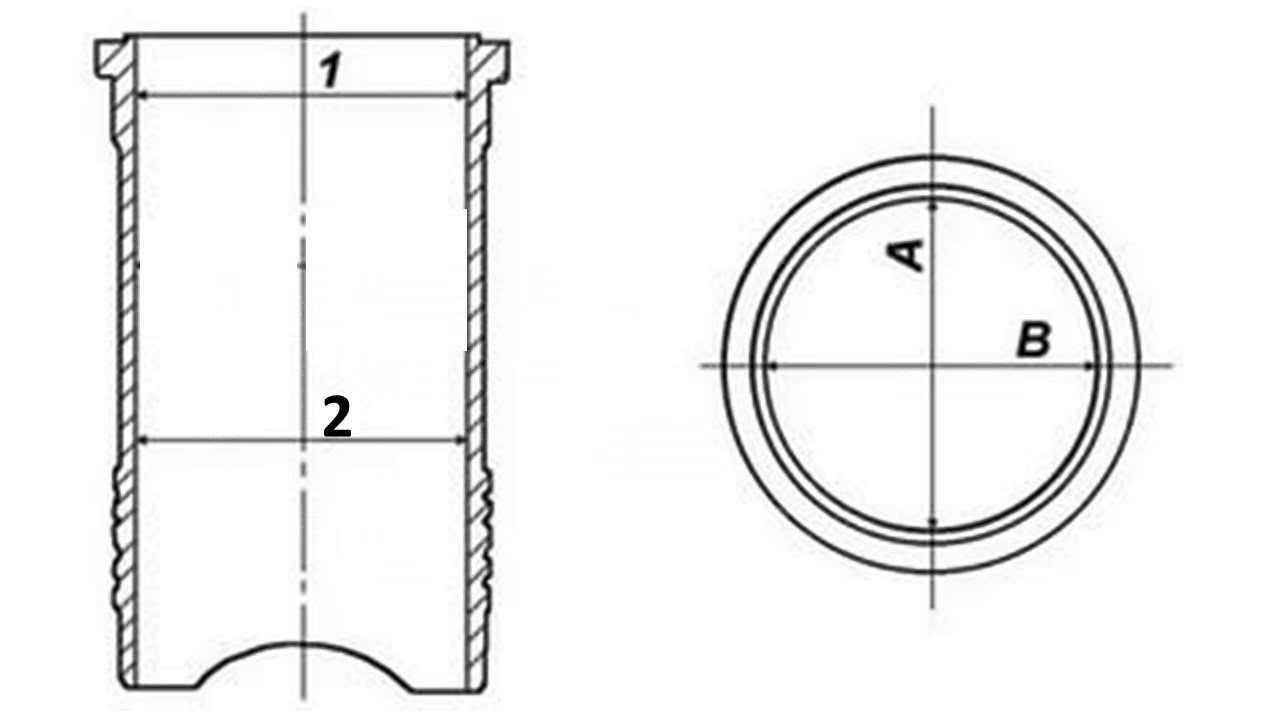

АКЦИЯ

Скидка 20%

действует на все слесарные работы автосервиса.

Как измерить цилиндр замка. Как определить размер цилиндра

Измерение замочного цилиндра, называемого также личинкой, вставкой или сердцевиной, является насущной необходимостью при его замене. Ведь, согласитесь, куда проще измерить длину цилиндра, а затем обзвонить магазины, узнав о наличии нужной модели, чем бегать с тем же цилиндром по тем же магазинам с неизвестным результатом, теряя свое время.

Обмер личинки не представляет особой сложности (цилиндр даже можно не вынимать замка) — главное знать что измерять, и какие цифры называть в магазине.

Чем измерить размер цилиндра

Для определения длины цилиндра профессионалы используют специальные устройства, которых по понятным причинам у нас нет. Поэтому измерения можно делать обычной линейкой — точности замеров вполне хватит для покупки или заказа новой личинки. Для замеров также сгодятся рулетка или штангенциркуль.

Как определить длину цилиндра

У любого цилиндра есть крепежное отверстие, которым личинка притягивается к корпусу замка. В совокупности с краями цилиндра, центр этого отверстия является точкой отсчета размера личинки. Размерность цилиндра (называемую также симметрией цилиндра) определяют три величины, в большинстве чертежей обозначаемые латинскими литерами A, B и C (или L), где:

A — расстояние от наружного края цилиндра до крепежного отверстия

B — расстояние от крепежного отверстия до внутреннего края цилиндра

C (или L) — общая длина цилиндра

Понятно, что сумма двух первых пунктов составляет общую длину цилиндра. Цилиндры, в которых расстояния от краев до отверстия равны, называются симметричными. В принципе, помнить литеры не нужно, главное — понимать что к чему в обозначениях длин цилиндров на сайтах и в описаниях. Симметрия цилиндра может обозначаться следующим образом: С(AxB), С(A/B) или просто A/B C. Единицы измерения — миллиметры.

Примеры измерений:

92(31х61) — цилиндр с общей длиной 92 мм. Расстояние от внешнего края до отверстия — 31 мм, от отверстия до внутреннего края — 61 миллиметр.

102(41/61) — цилиндр с общей длиной 102 мм. Расстояние от внешнего края до отверстия — 41 мм, от отверстия до внутреннего края — 61 миллиметр.

61/41 102 мм — тот же цилиндр с общей длиной 102 мм, но поменялись расстояния: от внешнего края до отверстия — 61 мм, от отверстия до внутреннего края — 41 миллиметр.

Завершая примеры, рассмотрим реальное обозначение — возьмем итальянский цилиндр Mottura Champions С38Р71/31. В замысловатом наборе символов можно заметить подозрительно знакомую пару цифр, разделенную слэшем — 71/31. Все верно, символы за литерой «P» и есть размерность цилиндра. Общая длина цилиндрового механизма не указывается, ибо она очевидна.

Как видим, в обозначениях симметрии, размеров и длин цилиндров нет ничего сложного.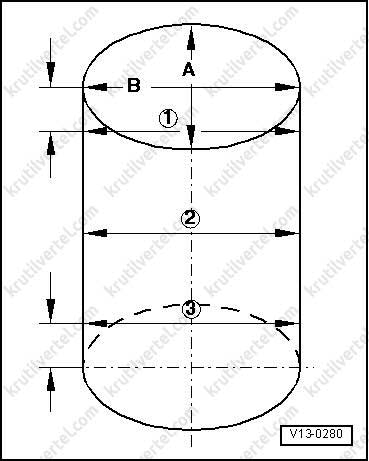 Не представляет особой сложности и самостоятельное определение размеров личинки — нужно лишь замерить линейкой или рулеткой три указанные величины.

Обмер цилиндра посредством линейки

Замер цилиндра штангель-циркулем

Обмер цилиндра при помощи специальной линейки

Наружная часть цилиндра Abloy помечена надписью «Outside»

При проведении замеров в некоторых случаях цилиндр даже можно не извлекать из двери, но существует несколько моментов, на которые стоит обращать внимание.

Следует знать, что на некоторых сайтах принят другой порядок обозначения симметрии цилиндра: А — внутренняя сторона, B — наружная (т. е. наоборот). Такие обозначения исключительно редки, встречаются лишь на иностранных сайтах, но при общении с менеджерами магазина лучше уточнить этот момент и оперировать терминами «внешняя сторона» и «внутренняя сторона».

Если вы решили самостоятельно сменить цилиндр (для человека мастерового такая работа не представляет особой сложности), то следует знать, что у некоторых равносторонних цилиндров параметры A и B — это не одно и то же. Да, длина их одинакова, но наружная, внешняя сторона может быть дополнительно усилена для повышения взломостойкости цилиндрового механизма.

В дешевых вариантах цилиндров и китайском ширпотребе не имеет значения, какой стороной устанавливать цилиндр, а вот имея дело с качественным брендовыми цилиндрами, имеющими с фасадной стороны защиту от высверливания, этот фактор нужно учитывать (читать о методах вскрытия цилиндров). Трудно представить, что цилиндр «ключ-ручка» можно установить ручкой наружу, а вот при исполнении цилиндра «ключ-ключ» ошибка вполне возможна — защитные элементы находятся в корпусе личинки. Поэтому производители высококлассных цилиндров каким-либо образом могут помечать наружную сторону личинок. К измерению цилиндра этот момент непосредственного отношения не имеет, но знания такого рода не помешают.

Цилиндр также можно подобрать непосредственно по дверному полотну, проведя измерения с торца полотна. При этом обязательно следует учитывать толщину элементов наружного и внутреннего оформления двери, включая толщину фурнитуры.

Если у вас дешевый китайский цилиндр, то следует убедиться, что размер его корпуса соответствует стандарту Euro DIN. Дело в том, что появились китайские цилиндры с уменьшенным размером корпуса. Решив заменить такую личинку, вы можете определить ее длину и купить нормальный механизм, который просто не влезет в замок.

Некоторые высококлассные личинки позволяют менять свою длину. Они собираются по модульной системе — в любом авторизованном сервис-центре вам изменят симметрию и новый цилиндр покупать не придется. Учитывая стоимость некоторых сердцевин, опция очень полезная.

Более добавить нечего. Замер личинки, в отличие от чтения статьи, займет у вас неизмеримо меньше времени. Особенно, если цилиндр при измерении не извлекается из двери.

Калькулятор объема цилиндра

Автор: Ханна Памула, доктор философии

Отзыв от Bogna Szyk и Jack Bowater

Последнее обновление: 12 февраля 2023 г.

Содержание:

Как рассчитать объем цилиндра?
Объем полого цилиндра
Объем наклонного цилиндра
Часто задаваемые вопросы

Наш калькулятор объема цилиндра позволяет вычислить объем этого твердого тела. Если вы хотите выяснить, сколько воды помещается в банку, кофе в вашу любимую кружку или даже объем соломинки для питья — вы находитесь в правильном месте. Другой вариант расчета объем цилиндрической оболочки (полый цилиндр).

Как рассчитать объем цилиндра?

Начнем с самого начала – что такое цилиндр? Это твердое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями. Мы можем представить его как твердую физическую банку с крышками сверху и снизу. Для расчета его объема нам необходимо знать два параметра – радиус (или диаметр) и высоту:

объем цилиндра = π × радиус цилиндра² × высота цилиндра

Калькулятор объема цилиндра помогает найти объем прямого, полого и наклонного цилиндра:

Объем полого цилиндра

Полый цилиндр, также называемый цилиндрической оболочкой, представляет собой трехмерную область, ограниченную двумя прямыми круглыми цилиндрами. с одной осью и двумя параллельными кольцевыми основаниями, перпендикулярными общей оси цилиндров.

Легче понять это определение, представив, например, соломинку для питья или трубку – полый цилиндр – это пластик, металл или другой материал. Формула объема полого цилиндра:

объем_цилиндра = π × (R² - r²) × высота_цилиндра

где R – внешний радиус, а r – внутренний радиус

Аналогично можно рассчитать объем цилиндра, используя внешний диаметр, 9002 9 Д , и внутренний диаметр d полого цилиндра по этой формуле:

объем_цилиндра = π × [(D² - d²)/4] × высота_цилиндра Примеры из реальной жизни, может быть... рулон туалетной бумаги, а почему бы и нет? 😀

Введите внешний диаметр цилиндра . Стандарт равен примерно 11 см.
Определить внутренний диаметр цилиндра . Это внутренний диаметр картонной детали около 4 см.
Узнать высоту цилиндра ; для нас это 9 см.
Тадаам! Объем полого цилиндра равен 742,2 см³.

Помните, что результатом является объем бумаги и картона. Если вы хотите посчитать, сколько пластилина можно положить внутрь картонного рулона, воспользуйтесь стандартной формулой объема цилиндра — калькулятор посчитает в мгновение ока!

`Объем косого цилиндра`

Косой цилиндр – это тот, который «наклоняется» – стороны не перпендикулярны основаниям, в отличие от стандартного «прямого цилиндра». Как рассчитать объем косого цилиндра? Формула такая же, как и для прямого. Только помните, что высота должна быть перпендикулярна основаниям.

Теперь, когда вы знаете, как рассчитать объем цилиндра, возможно, вы захотите определить объемы других трехмерных тел? Используйте этот общий калькулятор объема!

Если вам интересно, сколько чайных ложек или чашек поместится в ваш контейнер, воспользуйтесь нашим преобразователем объема.

Для расчета объема грунта, необходимого для цветочных горшков различной формы, в том числе для цилиндрического, воспользуйтесь калькулятором грунта.

`Часто задаваемые вопросы`

`Где можно найти цилиндры в природе?`

Цилиндры вокруг нас , и мы говорим не только о банках Pringles. Хотя вещи в природе редко бывают идеальными цилиндрами, некоторые примеры включают стволов деревьев и стебли растений, некоторые кости (и, следовательно, тела) и жгутики микроскопических организмов. Они составляют большое количество природных объектов на Земле!

`Как нарисовать цилиндр?`

Чтобы нарисовать цилиндр, выполните следующие действия:

Нарисуйте слегка приплюснутый круг. Чем он более сплющен, тем ближе вы смотрите на сторону цилиндра на .
Нарисуйте две равные параллельные линии от дальних сторон вашего круга, идущие вниз.
Соедините концы двух линий полукруглой линией, которая выглядит так же, как нижняя половина вашего верхнего круга.
При необходимости добавьте тень и штриховку.

`Как рассчитать вес баллона?`

Для расчета веса баллона:

Возведение в квадрат радиуса цилиндра .
Умножьте квадрат радиуса на число пи и высоту цилиндра .
Умножьте объем на плотность цилиндра. Результат – вес цилиндра.

`Как рассчитать отношение площади поверхности к объему цилиндра?`

Найдите объем цилиндра по формуле πr²h .
Найдите площадь поверхности цилиндра по формуле 2πrh + 2πr² .
Из двух формул составьте соотношение , т. е. πr²h : 2πrh + 2πr² .
В качестве альтернативы упростите его до rh : 2(h+r) .
Разделите с обеих сторон на одну из сторон, чтобы получить соотношение в его простейшей форме.

`Как найти высоту цилиндра?`

Если у вас есть объем и радиус цилиндра:

Убедитесь, что объем и радиус указаны в в тех же единицах (например, см³ и см), а радиус в радианах .
Квадрат радиус.
Разделите объем на квадрат радиуса и пи, чтобы получить высоту в тех же единицах, что и радиус.

Если у вас есть площадь поверхности и радиус (r):

Убедитесь, что поверхность и радиус указаны в тех же единицах , а радиус указан в радианах.
Вычтите 2πr² из площади поверхности.
Разделите результат шага 1 на 2πr.
Результат - высота цилиндра.

`Как найти радиус цилиндра?`

Если у вас объем и высота цилиндра:

Убедитесь, что объем и высота указаны в тех же единицах (например, см³ и см), а радиус — в радианах .
Разделите объем на число пи и высоту.
Квадрат корень результата.

Если у вас есть площадь поверхности и высота (h):

Подставьте высоту, h и площадь поверхности в уравнение, площадь поверхности = πr²h : 2πrh + 2πr².
Разделите с обеих сторон на 2π.
Вычтите площади поверхности/2π с обеих сторон.
Решите полученное квадратное уравнение.
Положительный корень — это радиус.

`Как найти объем прямоугольного трапециевидного цилиндра?`

Правильный трапециевидный цилиндр, также известный как прямоугольная призма , может быть решен следующим образом:

Сложите вместе две параллельные стороны (основания) трапеции.
Разделить результат на 2.
Умножьте результат шага 2 на высоту трапеции (т.е. расстояние, разделяющее две стороны).
Умножьте результат на длину цилиндра.
Результатом является площадь правильного трапециевидного цилиндра.

`Как найти объем овального цилиндра?`

Чтобы найти объем овального цилиндра:

Умножить наименьший радиус овала (малая ось) на его наибольший радиус (большая ось).
Умножьте это новое число на пи .
Разделите результат шага 2 на 4. Результатом будет площадь овала.
Умножьте площадь овала на высоту цилиндра.
Результат - объем овального цилиндра.

`Как найти объем наклонного цилиндра?`

Для расчета объема наклонного цилиндра:

Найдите радиус , длину стороны и угол наклона цилиндра.
Квадрат радиус.
Умножьте на число пи.
Возьмем грех угла .
Умножьте sin на длину стороны.
Умножьте на результат шагов 3 и 5 вместе.
В результате получается наклонный объем.

`Как рассчитать рабочий объем цилиндра?`

Для расчета рабочего объема цилиндра:

Разделите диаметр отверстия на 2, чтобы получить радиус отверстия .
Квадрат радиус отверстия.
Умножить радиус квадрата на число пи.
Умножьте результат шага 3 на длину штриха . Убедитесь, что единицы измерения диаметра и длины хода совпадают.
Результатом является рабочий объем одного цилиндра.

Ханна Памула, доктор философии

Прямой / наклонный полный цилиндр

Высота

Радиус

Диаметр

Объем

Полый цилиндр

Высота

Диаметр внешний

Диаметр внутренний

Объем

Посмотреть 23 похожих калькулятора 3d геометрии 📦

Площадь полушарияCubeCube Calc: найти v, a, d… 20 more

`Объем цилиндра - Формула`

Объем цилиндра — это вместимость цилиндра, которая рассчитывает количество материала, которое он может вместить. В геометрии существует специальная формула для расчета объема цилиндра, которая используется для измерения того, какое количество любого количества жидкости или твердого вещества может быть погружено в него равномерно. Цилиндр – это трехмерная фигура с двумя конгруэнтными и параллельными одинаковыми основаниями. Существуют разные типы цилиндров. Их:

Прямой круговой цилиндр: Цилиндр, основания которого представляют собой окружности, а каждый отрезок, являющийся частью боковой криволинейной поверхности, перпендикулярен основаниям.
Наклонный цилиндр: Цилиндр, стороны которого опираются на основание под углом, не равным прямому углу.
Эллиптический цилиндр: Цилиндр, основания которого представляют собой эллипсы.
Прямой круглый полый цилиндр: Цилиндр, состоящий из двух правильных круглых цилиндров, заключенных один внутри другого.

Формула для нахождения объема цилиндра: V = πr ² ч. Давайте узнаем больше об этой формуле в следующих разделах.

1.	Объем цилиндра
2.	Объем цилиндра Формула
3.	Как найти объем цилиндра?
4.	часто задаваемых вопросов по объему цилиндра 905:00

`Каков объем цилиндра?`

Объем цилиндра — это количество единичных кубов (кубов единичной длины), которые могут в него поместиться. Это пространство, занимаемое цилиндром, поскольку объем любой трехмерной формы - это пространство, занимаемое им. Объем цилиндра измеряется в кубических единицах, таких как см ³, м ³, в ³ и т. д. Давайте посмотрим формулу, используемую для расчета объема цилиндра.

`Определение цилиндра`

Цилиндр представляет собой трехмерное твердое тело, состоящее из двух параллельных оснований, соединенных изогнутой поверхностью. Эти основания имеют форму круглого диска. Линия, проходящая из центра или соединяющая центры двух круговых оснований, называется осью цилиндра.

`Объем цилиндра Формула`

Мы знаем, что цилиндр похож на призму (но обратите внимание, что цилиндр не является призмой, так как имеет изогнутую боковую грань), мы используем ту же формулу объема призмы, чтобы вычислить объем цилиндра. Мы знаем, что объем призмы рассчитывается по формуле

V = A × h, где

A = площадь основания
ч = высота

Используя эту формулу, формулы объема цилиндра :

Формула объема прямого кругового цилиндра: V = πr ² h (r = радиус, h = высота)
Формула объема наклонного цилиндра: V = πr ² h (r = радиус, h = высота)
Формула объема эллиптического цилиндра: V = πabh (a и b = радиусы, h = высота)
Формула объема прямого круглого полого цилиндра: V = π(R ² - r ² )h (R = внешний радиус, r = внутренний радиус, h = высота)

Теперь применим формулу V = A × h для расчета объема различных типов цилиндров.

`Объем правильного круглого цилиндра Формула`

Мы знаем, что основанием правильного круглого цилиндра является окружность, а площадь окружности радиуса r равна πr ² . Таким образом, объем (V) прямого кругового цилиндра, используя приведенную выше формулу (V = A × h), составляет

V = πr ² h

Здесь

'r' - это радиус основание (круг) цилиндра
'h' - высота цилиндра
π — это константа, значение которой равно 22/7 (или) 3,142.

Таким образом, объем цилиндра прямо зависит от его высоты и прямо зависит от квадрата его радиуса. т. е. если радиус цилиндра удвоится, то его объем удвоится.

`Формула для нахождения объема косого цилиндра`

Формула для вычисления объема цилиндра (наклонного) такая же, как и для прямого кругового цилиндра. Таким образом, объем (V) наклонного цилиндра, радиус основания которого равен r, а высота равна

V = πr ² h

`Формула для расчета объема эллиптического цилиндра что эллипс имеет два радиуса.`

Кроме того, мы знаем, что площадь эллипса, радиусы которого равны «а» и «b», равна πab. Таким образом, объем эллиптического цилиндра равен

V = πabh

Здесь

'a' и 'b' — радиусы основания (эллипса) цилиндра.
'h' - высота цилиндра.
π — это константа, значение которой равно 22/7 (или) 3,142.

`Объем прямого кругового полого цилиндра Формула`

Поскольку правильный круговой полый цилиндр представляет собой цилиндр, состоящий из двух прямоугольных круговых цилиндров, заключенных один внутри другого, его объем получается путем вычитания объема внутреннего цилиндра из объема внешний цилиндр. Таким образом, объем (V) прямоугольного полого цилиндра равен

V = π(R ² - r ² )h

Здесь

'R' — радиус основания внешнего цилиндра.
'r' — радиус основания внутреннего цилиндра.
'h' - высота цилиндра.
π — это константа, значение которой равно 22/7 (или) 3,142.

`Как найти объем цилиндра?`

Вот шагов, чтобы найти объем цилиндра:

Определите радиус как "r" и высоту как "h" и убедитесь, что они оба имеют одинаковые единицы измерения.
Подставьте значения в формулу объема V = πr ² ч.
Запишите единицы измерения в кубических единицах.

Пример: Найдите объем прямоугольного цилиндра радиусом 50 см и высотой 1 метр. Используйте π = 3,142.

Решение:

Радиус цилиндра равен r = 50 см.

Высота: h = 1 метр = 100 см.

Его объем V = πr ² h = (3,142)(50) ² (100) = 785 500 см ³ .

Примечание: Нам нужно использовать формулу, чтобы найти объем цилиндра в зависимости от его типа, как мы обсуждали в предыдущем разделе. Кроме того, предположим, что цилиндр является правильным круговым цилиндром, если не задан тип, и применим формулу объема цилиндра к V = πr ² h.

Важные примечания по объему цилиндра:

Объем цилиндра рассчитывается по формуле V = πr ² h, где r — радиус его круглого основания, а «h» — перпендикулярное расстояние (высота) между центрами оснований.
Если задан диаметр (d), найдите радиус (r), используя r = d/2, а затем подставьте в приведенную выше формулу, чтобы найти объем цилиндра.

`Объем цилиндра Примеры`

Пример 1: Найдите объем цилиндрического резервуара для воды в литрах, радиус основания которого 25 м, а высота 120 м. Используйте π = 3,14.
Решение:
Радиус цилиндрического резервуара r = 25 м.
Высота h = 120 м.
Используя формулу объема цилиндра, объем резервуара равен
V = πr ² h
V = (3,14)(25) ² (120) = 235500 куб.
Объем баллона в литрах получается по формуле преобразования 1 кубический метр = 1000 литров.
Таким образом, объем бака в литрах равен: 235500 × 1000 = 235 500 000
Ответ: Объем данного цилиндрического резервуара составляет 235 500 000 литров.
Пример 2: Рассчитайте объем эллиптического цилиндра, радиусы основания которого равны 7 дюймам и 10 дюймам, а высота равна 15 дюймам. Используйте π = 22/7.
Решение:
Радиусы основания данного эллиптического цилиндра равны
a = 7 дюймов и b = 10 дюймов.
Его высота h = 15 дюймов.
Используя формулу объема цилиндра, объем данного эллиптического цилиндра равен
V = πabh
V = (22/7) × 7 × 10 × 15 = 3300 кубических дюймов.
Ответ: Объем данного цилиндра составляет 3300 кубических дюймов.
Пример 3: Каков объем цилиндра с радиусом 4 единицы и высотой 6 единиц?
Решение:
Поскольку точный тип цилиндра не указан, мы должны предположить, что это правильный круговой цилиндр.
Радиус,r = 4 единицы и высота,h = 6 единиц
Объем цилиндра, V = πr ² h кубических единиц.
В = (22/7) × (4) ² × 6 В = 22/7 × 16 × 6
В = 301,71 куб.
Ответ: Объем цилиндра 301,71 куб.

перейти к слайдуперейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath.

Записаться на бесплатный пробный урок

`Практические вопросы по объему цилиндра`

перейти к слайдуперейти к слайду

`Часто задаваемые вопросы об объеме цилиндра`

`Что означает объем цилиндра?`

Объем цилиндра — это количество места в нем. Его можно получить, умножив площадь основания на высоту. Формула для нахождения объема цилиндра с радиусом основания «r» и высотой «h»: V = πr ² час.

`Какая формула для расчета объема цилиндра?`

Формула для расчета объема цилиндра: V = πr ² h, где

'r' — радиус основания цилиндра
'h' - высота цилиндра
π — константа, значение которой приблизительно равно 3,142.

`Каков объем цилиндра с диаметром?`

Рассмотрим цилиндр радиуса «r», диаметра «d» и высоты «h». Объем цилиндра с радиусом основания 'r' и высотой 'h' равен V = πr ² час. Мы знаем, что r = d/2. Подставив это в приведенную выше формулу, V = πd ² ч/4.

`Каково соотношение объемов цилиндра и конуса?`

Рассмотрим цилиндр и конус, каждый из которых имеет радиус основания «r» и высоту «h». Мы знаем, что объем цилиндра равен πr ² ч, а объем конуса равен 1/3 πr ² ч. Таким образом, требуемое соотношение равно 1:(1/3) (или) 3:1.

`Как рассчитать объем цилиндра с диаметром и высотой?`

Объем цилиндра с радиусом основания 'r' и высотой 'h' равен, V = πr ² h. Если диаметр основания равен d, то d = r/2. Подставляя это в приведенную выше формулу, мы получаем V = πd ² ч/4. Таким образом, формула для нахождения объема цилиндра с диаметром (d) и высотой (h) выглядит так: V = πd ² ч/4.

`Как найти объем цилиндра по окружности и высоте?`

Мы знаем, что длина окружности радиуса r равна C = 2πr. Таким образом, когда длина окружности основания цилиндра (C) и его высота (h) заданы, мы сначала решаем уравнение C = 2πr для 'r', а затем применяем формулу объема цилиндра, то есть V = πr ² час.

`Как рассчитать объем цилиндра в литрах?`

Мы можем использовать следующие формулы преобразования, чтобы преобразовать объем цилиндра из м ³ (или) см ³ в литры.

1 м ³ = 1000 литров
1 см ³ = 1 мл (или) 0,001 литра

☛ Чек:

Преобразование в метрическую систему
Преобразование единиц измерения

`Что произойдет с объемом цилиндра, если его радиус уменьшить вдвое?`

Объем цилиндра прямо пропорционален квадрату его радиуса. Таким образом, когда его радиус уменьшается вдвое, объем становится равным 1/4 ^th .

`Что происходит с объемом цилиндра, когда его радиус увеличивается вдвое?`

Мы знаем, что объем цилиндра прямо пропорционален квадрату его радиуса. Таким образом, когда его радиус увеличивается вдвое, объем увеличивается в четыре раза.

`Как найти объем цилиндра с помощью калькулятора?`

Калькулятор объема цилиндра - это машина для расчета объема цилиндра. Чтобы рассчитать объем цилиндра с помощью калькулятора, нам необходимо предоставить необходимые данные для инструмента калькулятора, такие как требуемые размеры, такие как радиус, диаметр, высота и т. д. Попробуйте сейчас вычислить объем цилиндра, введите радиус и высоту цилиндра. в данном ящике объем цилиндра вычислитель. Нажмите на кнопку «Рассчитать», чтобы найти объем цилиндра. Нажав кнопку «Сбросить», вы можете легко очистить ранее введенные данные и найти объем цилиндра для разных значений.

☛Также проверьте:

Калькулятор цилиндров
Калькулятор площади поверхности цилиндра
Калькулятор высоты цилиндра

`Что такое площадь и объем цилиндра?`

Площадь поверхности цилиндра – это общая площадь или область, покрываемая поверхностью цилиндра. Площадь поверхности цилиндра определяется двумя следующими формулами:

Площадь криволинейной поверхности цилиндра = 2πrh
Общая площадь поверхности цилиндра = 2πr ² +2πrh = 2πr(h+r)

Площадь цилиндра выражается в квадратных единицах, например, в м ², в ², см ², ярдах ² и т. д.

Объем цилиндра равен общей вместимости ред. в цилиндре, который можно рассчитать с помощью уравнения объема цилиндра, равен V = πr ² ч и измеряется в кубических единицах.

☛ Чек:

Площадь поверхности цилиндра Листы
Объем цилиндра Рабочие листы
Формулы площади поверхности

`Как изменится объем полого цилиндра при удвоении высоты?`

Формула объема полого цилиндра равна V = π(R ² - r ² )h кубических единиц. Из формулы объема видно, что объем прямо пропорционален высоте полого цилиндра. Следовательно, объем удваивается, когда высота полого цилиндра удваивается.

Posted inЦилиндр