Так как у нас имеется электродвигатель марки 4А200М6УЗ с частотой вращения 
, то момент инерции ротора двигателя по [3.с.914]:
.
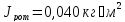По [3, c.678] для дальнейших расчетов примем диаметры и длину выходных концов валов как:
мм;
мм;
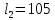мм;
мм.
Так как 
≤200 мм принимаем диаметры валов под подшипниками и под колесами как:
мм;
мм.
Для нахождения момента инерций колес найдем длину нарезаемой части и диаметры колеса и шестерни:
Следовательно, длины валов без колеса или шестерни равны:
мм.
Диаметр шестерни примем диаметром вала быстроходной ступени:
мм.
Диаметр колеса:
5.4. Расчет момента инерции шестерни
Для расчета моментов используем формулу:
,
где d-диаметр шестерни;
b-длина нарезаемой часть;
p-плотность материала изготовления.
5.4.1. Момент инерции выходного конца шестерни
5.4.2. Момент инерции вала без шестерни
5.4.3. Момент инерции шестерни
5.5. Суммарный момент инерции на шестерне 
5.6. Расчет момента инерции зубчатого колеса
5.6.1. Момент инерции выходного конца зубчатого колеса
5.6.2. Момент инерции вала без зубчатого колеса
5.6.3. Момент инерции зубчатого колеса
5.7. Суммарный момент инерции на зубчатом колесе
5.8.1. Быстроходный шкив
где
- плотность чугуна,В – ширина обода, - 
диаметр шкива.
5.8.2. Тихоходный шкив
где
диаметр шкива.5.9. Момент инерции муфты
Типоразмер муфты подбирают по диаметру вала и по величине расчетного вращающегося момента:
,
где 
- коэффициент, учитывающий условия эксплуатации.
Примем 
=2, тогда
H⋅м;
H⋅м.
По ГОСТ Р 50895-96 берем зубчатую муфту с вращающим моментом равным 
5.10. Приведенный момент инерции к валу электродвигателя
.
1.Чернавский С.А. и др. Курсовое проектирование деталей машин. -М.:Машиностроение,1988.-416 с.:ил.
2. Анурьев В.И.Справочник конструктора-машиностроителя: в 3-х т.Т.3.-М.:Машиностроение,2006.-928c.:ил.
3. Анурьев В.И.Справочник конструктора-машиностроителя: в 3-х т.Т.2.-М.:Машиностроение,2006.-960c.:ил.
4. Методические указания к разработке и оформлению курсовых проектов и работ по дисциплинам «Механика», «Прикладная механика», «Детали машин и основы конструирования», сост. В.Я. Баранцов, Т.Г. Зайцева.-Липецк: ЛГТУ, 2002. – 31 с.
studfiles.net
| 1.Состав и назначение систем автоматизированного электропривода. Электромеханическое устройство для преобразования электрической энергии в механическую и управления преобразуемой энергией называется электроприводом. На рисунке 1.1 представлена полная функциональная схема автоматизированного электропривода производственного механизма. Система управления СУ привода, включающая в себя силовую (ССУ) и информационную (ИСУ) систему управления, которые получают питание от сети с параметрами Uc,Ic,fc и преобразует их для питания двигателя ЭД в соответствии с режимом работы последнего. Передаточный механизм ПМ служит для преобразования механических параметров на валу ЭД – момента МВ и частоты вращения ωВ и передачи их исполнительному механизму ИМ. В замкнутых системах АЭП сигнал управления формируется при сравнении сигналов задающего устройства (ЗУ) и датчиков обратных связей (ДОС). В конкретных агрегатах могут отсутствовать отдельные элементы схемы. Примером ПМ может служить редуктор для преобразования угловой частоты вращения (рисунок 1.2, а) в соответствии с передаточным числом i = ωВЫХ/ωВХ. ПМ может также служить для преобразования вращательного движения вала двигателя с частотой ω в возвратно – поступательное с линейной скоростью V (рисунок 1.2, b, c). | 2.Уравнение движения электропривода, вывод и анализ Рассмотрим простейшую механическую систему, состоящую из вращающейся части двигателя (ротора или статора - РД) и рабочего органа (РО) механизма, имеющего вращательное движение, присоединенного непосредственно к валу двигателя. В системе действуют два момента: момент, развиваемый двигателем МД, и момент статической нагрузки МС, в который входят момент, создаваемый рабочим органом механизма, и моменты трения. Эти моменты характеризуются величиной и направлением действия. Если МД и МС действуют в направлении движения, их называют движущими, если их знаки противоположны знаку скорости, моменты называют тормозящими. В соответствии с принципом Деламбера, совместное действие МД и МС определит величину и знак динамического момента Проведем простейший анализ уравнения (1) для двигательного режима работы ЭП, когда При МД > МС dω/dt > 0 и имеет место режим ускорения привода, при МД < МС dω/dt < 0 и имеет место режим замедления привода, а при МД = МС динамический момент и ускорение равны нулю. Первые два режима называют переходными, а последний – установившимся (стационарным). |
| 3. Понятие о статической устойчивости работы привода. Обычно между ЭД и РО находится одно или несколько передаточных устройств (ПУ). На рисунке 1.4 представлена кинематическая схема электропривода подъемного механизма, в котором в общем случае могут быть использованы i редукторов (ПУ1 – ПУi) для снижения частоты вращения и барабан, преобразующий вращательное движение в возвратно – поступательное. Валы этих устройств соединены с помощью соединительных муфт СМ. Все элементы схемы движутся с различными скоростями и ускорениями и имеют свои моменты инерции, что затрудняет составление и анализ уравнения движения всей системы. Поэтому на практике все моменты статической нагрузки и моменты инерции приводятся к какому – либо одному валу, обычно к валу двигателя и относительно этого вала решают уравнение движения. Таким образом, необходимо перейти от данной схемы к схеме на рисунке 1, где МС и J – суммарные величины, приведенные к валу ЭД. При приведении моментов статической нагрузки исходим из равенства мощности в реальной и приведенной схемах: При возвратно – поступательном движении Суммарный приведенный к валу двигателя момент сопротивления При приведении моментов инерции исходим из равенства запасов кинетической энергии в реальной и приведенной схемах. При вращательном движении При возвратно – поступательном движении Где Суммарный приведенный к валу двигателя момент инерции | |
| 4. Типовые статические нагрузки электропривода. Активные и реактивные силы и моменты нагрузки Механическая характеристика исполнительного механизма – зависимость Мс=f(ω). Активными силами и моментами называются силы и моменты, создаваемые внешними по отношению к двигателю источниками механической энергии независимо от движения электропривода. Пример – момент, создаваемый весом опускаемого или поднимаемого груза (рисунок 1). Момент сопротивления при этом равен и направлен вниз, независимо от направления вращения вала двигателя. Величина МС не зависит от скорости Рисунок 2.1 перемещения груза. Реактивными силами и моментами называются силы и моменты сопротивления движению, возникающие как реакция на активный движущий момент, развиваемый двигателем. Реактивные силы и моменты зависят от скорости и подразделяются на силы и моменты сухого трения, вязкого трения и силы, и моменты вентиляторного типа. Силы и моменты сухого трения (рисунок 2.2) неизменны по модулю, но скачком меняют свой знак при изменении знака скорости: Зависимость нагрузочного момента от угловой скорости вентилятора, центробежного насоса, центрифуги имеет вид, показанный на рисунке 2.4, называется вентиляторным и описывается формулой Механическая характеристика электродвигателя – зависимость М=f(ω). Из курса «Электрические машины» знаем, что механические характеристики ЭД (рисунок 5) могут быть абсолютно жесткими (1- синхронный ЭД), жесткими (3 – двигатель постоянного тока независимого возбуждения и 2 – асинхронный двигатель на рабочем участке) и мягкими (4 - двигатель постоянного тока последовательного возбуждения). Абсолютной жесткостью характеристики называется отношение приращения момента к приращению скорости | |
В системе действуют два момента: момент, развиваемый двигателем МД, и момент статической нагрузки МС, в который входят момент, создаваемый рабочим органом механизма, и моменты трения. Эти моменты характеризуются величиной и направлением действия. Если МД и МС действуют в направлении движения, их называют движущими, если их знаки противоположны знаку скорости, моменты называют тормозящими. В соответствии с принципом Деламбера, совместное действие МД и МС определит величину и знак динамического момента 
, определяющего ускорение системы. Таким образом, уравнение движения системы в общем случае имеет вид
.
Проведем простейший анализ уравнения (1) для двигательного режима работы ЭП, когда
.
При МД > МС dω/dt > 0 и имеет место режим ускорения привода, при МД < МС dω/dt < 0 и имеет место режим замедления привода, а при МД = МС динамический момент и ускорение равны нулю. Первые два режима называют переходными, а последний – установившимся (стационарным).
При приведении моментов статической нагрузки исходим из равенства мощности в реальной и приведенной схемах:
, Откуда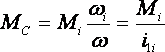 
.
При возвратно – поступательном движении
, и 
Суммарный приведенный к валу двигателя момент сопротивления
При приведении моментов инерции исходим из равенства запасов кинетической энергии в реальной и приведенной схемах. При вращательном движении
При возвратно – поступательном движении
; 
, где
;
.
Суммарный приведенный к валу двигателя момент инерции
7. Естественные электромеханические и механические характеристики двигателей постоянного тока независимого возбуждения
8. Построение естественных электромеханических и механических характеристик двигателей постоянного тока независимого возбуждения
9. Искусственные электромеханические и механические характеристики двигателей постоянного тока независимого возбуждения при изменении сопротивления цепи якоря
10. Искусственные электромеханические и механические характеристики двигателей постоянного тока независимого возбуждения при изменении напряжения якоря.
11. Искусственные электромеханические и механические характеристики двигателей постоянного тока независимого возбуждения при изменении магнитного потока.
12. Режимы торможения двигателей постоянного тока независимого возбуждения. Электродинамическое торможение.
13. Режимы торможения двигателей постоянного тока независимого возбуждения. Торможение противовключением.
14. Режимы торможения двигателей постоянного тока независимого возбуждения. Рекуперативное торможение.
Электромеханические и электромагнитные процессы в ДПТ НВ (рисунок 1) описываются уравнениями электрического равновесия (Кирхгофа) цепей якоря и обмотки возбуждения, а также уравнением электромагнитного момента:
Из совместного решения системы уравнений получаем уравнение электромеханической характеристики ω = f(I)
и уравнение механической характеристики ω = f(M)
В установившемся режиме работы привода
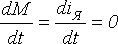, и уравнения приобретают вид 
Характеристики, построенные при номинальных значениях напряжения и потока и Rдоб =0, называются естественными, при UЯ ≠UН, Ф≠ФН или Rдоб ≠0 – искусственными электромеханическими или механическими характеристиками. Характерными точками электромеханической характеристики (рисунок 2) являются точки идеального холостого хода (I=0, ω=ω0=UН/kФН), короткого замыкания (I=IК=UН/RЯΣ, ω=0) и номинального режима (IЯ=IН, ω=ωН). По любой паре из этих координат можно построить характеристику.
Используя введенные значения жесткости характеристик
; 
можно записать следующие выражения для электромеханических и механических характеристик:
; 
;
Режимы работы привода, приведенные на рисунке 2, поясняются ниже.
В двигательном режиме работы (рисунок 2.9) ЭД потребляет энергию из электрической сети и передает на вал механическую энергию. В режиме противовключения (рисунок 2.10) ЭД потребляет энергию, накопленную механизмом, и рассеивает в элементах двигателя и добавочных сопротивлениях. В режиме рекуперативного (генераторного) торможения (рисунок 2.5) ЭД потребляет энергию, накопленную механизмом, и передает ее в электрическую сеть.
При Rдоб ≠0 получаем искусственные реостатные электромеханичеcкие характеристики. Увеличение в (2.4, 2.5) RЯΣ приводит к уменьшению величины тока короткого замыкания (IК=UН/RЯΣ) при неизменной скорости холостого хода ω0=UН/kФН (рисунок 3.1). При неизменном магнитном потоке Ф=ФН, механические характеристики будут аналогичны эл.механическим.
Магнитный поток машины можно изменять только в сторону уменьшения. При этом скорость холостого хода ω0=UН/kФН возрастает при неизменном значении тока короткого замыкания IК=UН/RЯΣ (рисунок 3.2 – электромеханическая характеристика при Ф - var). Момент короткого замыкания МК=kФIК при Ф - var снижается. Механическая характеристика изображена на рисунке 3.3.
Напряжение, подаваемое на якорь машины, можно изменять только в сторону уменьшения от номинального значения. При этом пропорционально напряжению снижаются и скорость холостого хода ω0=UН/kФН , и значение тока короткого замыкания IК=UН/RЯΣ (рисунок 3.4 – электромеханическая характеристика при U - var). Момент машины М=kФI при Ф-const пропорционален току якоря и механическая характеристика имеет аналогичный вид.
В соответствии с рассмотренными режимами работы электропривода, следует выделить следующие способы торможения ДПТ НВ:
a) рекуперативное торможение (с отдачей энергии в сеть)
Направление действия электромагнитного момента электрической машины определяется направлением тока якоря ДПТ и магнитного потока (1.1 в лекции №1). В соответствии с 1.1, ток якоря
,
и его знак зависит от соотношения ЭДС якоря и питающего напряжения. При
момент положителен и машина работает в двигательном режиме. При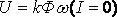 
- холостой ход, и при
машина работает в генераторном режиме (режим рекуперации мощности в сеть). Для обеспечения рекуперативного торможения необходимо, чтобы частота вращения вала ω была больше скорости холостого хода при данной схеме включения и параметрах питания двигателя. На рисунке 3.5 представлены механические характеристики ДПТ НВ грузоподъемного механизма, работающего в режиме рекуперативного торможения;
б) Электродинамическое торможение
На рисунке 3.6 представлена схема электродинамического торможения ДПТ НВ. Якорь двигателя отключен от сети и замкнут на дополнительное тормозное сопротивление RТ, обмотка возбуждения подключена к источнику питания. При этом ток якоря меняет знак на обратный
.
Взаимодействуя с потоком возбуждения, ток якоря образует момент, направленный против скорости вращения якоря двигателя. Уравнения электромеханической и механической характеристик принимают вид
; 
.
Механическая характеристика в режиме динамического торможения (рисунок 3.7) проходит через начало координат. По мере снижения скорости тормозной момент уменьшается, и в случаях необходимости повысить его величину при сниженных скоростях прибегают к двух- или даже трехступенчатому торможению, уменьшая ступенями сопротивление якорной цепи двигателя по мере снижения его скорости;
C) торможение противовключением
В режиме противовключения изменяет знак скорость двигателя при сохранении знака момента или знак момента двигателя при сохранении знака скорости. Первый случай имеет место при воздействии активного момента статической нагрузки, превышающего момент короткого замыкания на данной характеристике (рисунки 3.7, 3.8).
В результате изменения знака скорости ЭДС двигателя будет совпадать с приложенным напряжением, и ток в якоре определится, как
.
Этот режим используется в подъемных установках для спуска груза с малыми скоростями («силовой спуск»).
Режим противовключения чаще используется для остановки или изменения направления вращения двигателя путем перемены полярности напряжения, подводимого к якорю (рисунки 3.9, 3.10). При этом ток якоря изменит направление на обратное, изменится соответственно и знак момента двигателя, который будет направлен, до остановки двигателя, в сторону, противоположную скорости:
.
studfiles.net
Не всегда значение маховых моментов или моментов инерции роторов или якорей электрических машин можно найти в каталогах электрооборудования. Также в данный момент на предприятиях эксплуатируется большое количество электрических машин, данные на которые могут потеряться в ходе эксплуатации. Если данные о маховом моменте электрической машины отсутствуют, то их можно определить экспериментально с помощью методов:
Содержание:
Суть данной методики заключается в следующем: ротор электромашины подвешивают на стальной проволоке за конец вала. Второй конец проволоки жестко закрепляют на опоре, как показано на рисунке ниже (а):
При таком определении момента инерции нужно строго обеспечить вертикальность оси вала ротора. После чего ротор, подвешенный на проволоке, закручивают на определенный угол и подсчитывают количество полных колебаний z, которые ротор совершит за какой – то промежуток времени t. Период полного колебания, если пренебречь затуханием, можно представить:
Где k – направляющий момент проволоки (момент, вызывающий закручивание проволоки на 1 радиан). Если мы знаем k, то момент инерции ротора можно определить из следующего выражения:
k можно определить исходя из размеров проволоки:
Где Е – модуль кручения для материала проволоки в кГ/см2;
r и l – радиус и длина проволоки в см соответственно.
Так как формула не дает точного значения k, более точно можно определить его из опыта. Для этого нужно измерять вращающий момент М, необходимый для закручивания проволоки на угол α. Тогда:
Но еще проще произвести определение момента инерции на основе двух опытов крутильных колебаний ротора. Для этого измеряют продолжительность полного колебания как указано выше. Второе измерение периода колебания ротора производят с прикрепленным к нему телом, момент инерции которого известен Jдоб. Как вариант, это может быть диск с известными геометрическими размерами и весом или рычаг с грузами на концах (рис. выше б). если Т – период колебаний одного ротора, а Т/ — с добавочным грузом, тогда получим выражение:
Благодаря пропорциональности между углом отклонения и направляющим моментом угол первоначального закручивания может быть взят произвольным.
Ротор машины крепят проволокой к куску угловой стали так, чтоб вершину уголка можно было использовать в качестве призмы, относительно которой ротор электромашины смог бы выполнять колебания. После чего оба конца полученного таким образом маятника опирают на металлические горизонтальные опоры так, чтоб ротор мог относительно точек опоры совершать колебания. Момент его инерции относительно оси, совпадающей с вершиной уголка, при пренебрежении инерцией последнего будет равен:
Где: G – это вес ротора машины в кг;
е – расстояние между осью ротора и осью качания, измеряется в м;
Т – период одного колебания в сек.
Зная JN, определяют по общему правилу инерцию ротора относительно оси, проходящей через центр тяжести:
Самым главным недостатком методик, описанных выше, является то, что для определения инерции необходима разборка электромашины. Метод падающего груза позволит определить момент инерции электродвигателя без разборки последнего.
На конец вала или шкив, сидящий на валу, навивают несколько витков шнура. К другому концу шнура прикрепляют груз и опускают его через направляющие блоки, либо непосредственно, как показано ниже:
При опускании груз поворачивает ротор, преодолевая трение в подшипниках электромашины, при этом измеряют время t, за которое груз опустится на величину h.
В таком случае инерция ротора может быть вычислена по формуле:
Где: m – масса груза 
r – радиус вала или шкива, на который навивается шнур;
t и h – время, и соответственно высота опускания груза;
g – ускорение свободного падения равное 9,81;
Перечисленные выше методы определения инерции электрической машины больше подходят к электрическим машинам относительно малой мощности. При значительных габаритных и массовых показателей машин большой мощности определение инерции методами маятниковых колебаний и падающего груза становятся практически не пригодными, и тем более не пригодны в системе электродвигатель – рабочий орган. Поэтому зачастую применяют метод свободного выбега.
Когда двигатель отключают от сети, то за счет накопленной кинетической энергии, двигатель и соединенный с ним рабочий орган будет вращаться замедляясь постепенно. Чем больше тормозящее усилие сил трения и чем меньше запас кинетической энергии, тем быстрее будет замедлятся система. Имея кривую самоторможения, показанную ниже, которая представляет собой график зависимости скорости от времени.
По данной кривой можно сделать вывод о величине тормозных усилий. Мощность торможения в данном случае будет равна уменьшению кинетической энергии во времени:
Подставив в формулу значение кинетической энергии 
, которая представлена в джоулях, тогда получим:
Из данного выражения можно определить момент инерции:
Величину поднормали 
определяют из кривой торможения для точки, в которой известны потери энергии при торможении. Если масштабы выбраны, то для построения кривой самоторможения: µn = об/мин/см – скорость, µt = сек/см – времени. В таком случае масштаб поднормали будет равен: 
, то есть 
, где СВ выражена в см.
elenergi.ru
Нагрузка двигателя – основной фактор, оценивающий потери энергии, выделяющиеся в двигателе, и его нагрев при работе. Согласно основным уравнениям движения она зависит от статической нагрузки и от динамических моментов, обусловленных изменениями скорости электропривода
.
1.1. Ориентировочный выбор электродвигателя.
где 
, - заданный момент и статического сопротивления соответственно в начале и конце рабочего цикла;m, n - число одновременно работающих механизмов и электродвигателей, соответственно; 
- установившаяся угловая скорость движения рабочего механизма;i и - соответственно, передаточное отношение и КПД механической передачи; уст - установившаяся угловая скорость двигателя, определяемая как 
Угловая скорость двигателя в установившемся режиме:
,
где 
с-1- угловая скорость рабочей машины в установившемся режиме.
По среднему значению приведенного к валу двигателя статического момента 
определяем требуемую среднюю мощность электродвигателя:
- средняя мощнось электродвигателя
кНм
где 
- коэффициент запаса, учитывающий влияние динамических моментов и ухудшение вентиляции двигателя (если выбирается двигатель с самовентиляцией) в периоды пауз, разбега и торможения.
кВт
При заданной частоте вращения 
и средней мощности
по каталогу выбираем двигатель
Двигатель : 4ПФ250М
Из каталога выписываем все необходимые данные принятого двигателя, включая момент инерции 
или маховый момент
двигателя. На основании этих данных рассчитываем параметры, необходимые для дальнейших расчетов, и результаты заносим в таблицу:
Технические данные двигателя постоянного тока
| Тип двигателя | Мощность Pном,кВт | Напряжение якоря Uном,В | Номинал. частота вращения nном,об/мин | КПД ном, % | Ток якоря Iном,А | Момент Mном,Нм | Суммарное сопротивление якоря Rя,Ом | Сопротивление обмотки возбуждения Rв,Ом | Допустмая перегрузка по току Iдоп /Iном | Момент инерции Jдв,кгм2 |
При наличии каталожных данных о сопротивлении обмотки якоря Rо.я и сопротивлении добавочных полюсов Rд.п. сопротивление якорной цепи определяем как Rя=Rо.я+Rд.п. В случае если в каталоге сопротивление якоря не указано, то его ориентировочно определяем, принимая, что половина всех потерь в двигателе при номинальной нагрузке связана с потерями в меди якоря
.
Если в каталоге для двигателей указывается значение махового момента GD2 (кгсм2 или Нм2), определение момента инерции ротора двигателя выполняется согласно таблице пересчета единиц измерения.
Таблица . Пересчет единиц измерения
| GD2 | кгсм2 | Нм2 |
| J, кгм2 | GD2/4 | GD2/4g |
*Примечание: g = 9,807 м/с2
Наличие номинальных данных позволяет приступить к расчету нагрузочной диаграммы двигателя. При расчете нагрузочной диаграммы для целей проверки двигателя по нагреву можно пренебречь электромагнитными переходными процессами и учесть динамические нагрузки на основе тахограммы привода (диаграммы скорости электропривода) 
3.1. Для построения зависимости 
определяем время разгона и замедления при постоянном ускорении наi-м периоде диаграммы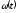 
,
где 
- начальное и конечное значения угловой скорости рабочей машины на данном участке;
- угловое ускорение (замедление) рабочей машины наi-м участке диаграммы, определяемое как 
; ( время на третьем участке)
(время на четвертом участке).
(время на пятом участке).
(время на седьмом участке).
3.2. Нагрузочная диаграмма двигателя M=f(t) (рис.3d) может быть получена в результате суммирования статического и динамического моментов 
. Поэтому значение требуемого момента на валу двигателя вi-й точке диаграммы определяем из уравнения движения:
,
где Mci – момент статического сопротивления, J - суммарный момент инерции системы, приведенный к валу двигателя. Для этого предварительно рассчитывают Mci в i-й точке нагрузочной диаграммы рабочего механизма, соответствующей началу или концу каждого участка тахограммы1, а так же приведенный момент инерции:
( момент на третьем участке).
( момент на пятом участке).
(момент на седьмом участке).
(номинальный момент)
.
,
где m – число одновременно работающих механизмов,
. 
3.3.Диаграмма токов
.
; ( номинальный ток для двигателя).
; (ток на третьем участке).
; (ток на пятом участке).
; (ток на седьмом участке).
Установившийся режим:
(ток на четвертом участке).
3.4 Режим работы электропривода
Построенные нагрузочные диаграммы позволяют обосновать и выбрать режим работы двигателя на каждом участке.
Если в период замедления момент положительный, применяем торможение в двигательном режиме. Если момент отрицательный, применяем динамическое торможение.
Если в диаграмме в период замедления тормозной момент 
, с относительно небольшой ошибкой времени торможения принимаем торможение свободным выбегом.
3.5. Проверка выбранного двигателя
Продолжительность включения
,
где полное время цикла работы
.
Т.к ПВ60%, двигатель проверяют как для длительного режима.
Полное время цикла работы
.
Номинальное значение угловой скорости:
= 104 
Сопротивление якорной цепи двигателя:
Ом
studfiles.net
Выбор двигателя для САУ
Момент инерции системы, приведенный к валу двигателя, вычисляется по следующей формуле (см...
Динамика вращения твердого тела на примере диска и шара радиусом R
Дифференциал массы равен моменту инерции этого кольца: (1.9) Рис. 1.1 Тогда масса кольца определяется: (1.10) Дифференциал момента инерции равен моменту инерции этого кольца: (1.11) Отсюда следует: (1.12) Момент инерции диска равен: (1...
Динамика вращения твердого тела на примере диска и шара радиусом R
Разобьём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле (1.14) Рис. 1.2 Масса и момент инерции такого диска составят (1.15) (1...
Дифференциальные уравнения движения механической системы
Главным моментом количеств движения (кинетическим моментом) системы относительно центра А называется величина:...
Макромоделирование асинхронных машин с учетом динамики
С целью выявить факторы, требующие учета в моделировании динамических режимов асинхронных машин...
Проектирование асинхронного двигателя
259. Масса изолированных проводов обмотки статора, кг 270. Масса стали сердечника статора и ротора, кг 271. Масса изоляции статора, кг где bп-средняя ширина паза, мм 273. Масса конструкционных материалов двигателя со степенью защиты IP44, при h?200 мм...
Проектирование электропривода механизма перемещения
Общий момент инерции механизма и груза, приведенный к валу двигателя определяют по формуле [6, с.10]: J = 1,3(JЯ+JМ)+JГ (28) где JЯ - момент инерции якоря двигателя, кгм2; JM - момент инерции муфты, помещенной между двигателем и редуктором...
Проектирование электропривода механизма подъема крана
Электромеханическая характеристика электропривода с асинхронным двигателем: , (4.1) где - значение тока ротора, приведенное к обмотке статора, А. Максимальное значение тока ротора двигателя, при подъеме груза и спуске крюка: ,(4...
Расчет основных элементов и характеристик асинхронного двигателя
; откуда момент...
Синхронный генератор
...
Техническая эксплуатация и ремонт двигателей постоянного тока
Если обмотку возбуждения и якорь двигателя подключить к сети постоянного тока напряжением U то, возникает электромагнитный вращающий момент Мэм...
Функционирование заданной кинематической схемы асинхронного электродвигателя АКН 15-44-10
Момент инерции барабана: , где T•м2 - маховый момент барабана, кг•м2. Момент инерции шестерней №2, №3: , . кг•м2. кг•м2. Момент инерции системы: , кг•м2...
Электрический привод мостового крана
Приведенный к валу электродвигателя момент инерции системы J кг•м2, определяется по формуле где k - коэффициент, учитывающий момент инерции механической передачи, k = 1,05-1,2; Jд - момент инерции ротора электродвигателя...
Электропривод пассажирского подъемника
Противовес для лифтов выбирается с таким расчётом, чтобы он уравновешивал вес подъёмного сосуда (кабины) и часть номинального поднимаемого груза: где б - коэффициент уравновешивания, обычно принимается равным 0.4 - 0.6. отсюда следует, что кг...
Электропривод перемещения моста крана с преобразователем частоты
Суммарный момент инерции системы электропривод - рабочая машина приведенный к валу электродвигателя рассчитывается по соотношению: где =1,5 - коэффициент, учитывающий моменты инерции муфты, тормозного шкива...
fis.bobrodobro.ru
При составлении расчетной схемы механической части электропривода
моменты сопротивления движению РО (статические моменты) и моменты
инерции приводятся к валу двигателя.
Критерием приведения моментов к валу двигателя является энергетический баланс механической части электропривода. Статические и динамические моменты на валу рабочей машины приведены в таблице 5
Выбран редуктор с передаточным числом iР=40 и коэффициентом полезного
действия ηР=0.97
Статический момент рабочей машины, приведенный к валу двигателя, без учета потерь в редукторе (ηР= 1), рассчитывается по формуле:
; (12)
Статические моменты на валу с учетом потерь в редукторе (ηР < 1) рассчитываются в зависимости от режима работы электропривода.
Статический момент на валу в двигательном режиме
; (13)
При работе электропривода в тормозных режимах потери в редукторе
вызывают уменьшение нагрузки двигателя, при этом моменты на валу определяются по формуле:
;(14)
Приведённые моменты к валу двигателя рассчитываются приближенно, принимая в расчетах номинальное значение коэффициента полезного действия редуктора ηР.
При уточненных расчетах установившихся и переходных режимов
работы электропривода необходимо также учитывать момент потерь холостого хода (момент постоянных потерь) двигателя 
.
В двигательном режиме работы двигателя статический момент
увеличивается на величину момента потерь холостого хода
покрывается за счет электромагнитного момента двигателя:
При работе двигателя в тормозном режиме статический момент
уменьшается на величину момента потерь холостого хода
(
покрывается за счет статического момента рабочего органа).
Таким образом, приведенные статические моменты системы
электропривод – рабочая машина рассчитывают для каждого участка с
учетом режима работы электропривода по формуле :
МС = МВС ± 
, (15)
где 
рассчитывается по формуле:
При этом в статическом моменте учитываются не только силы сопротивления движению в рабочей машине, но также и потери в редукторе и механические потери в двигателе.
Суммарный приведенный к валу двигателя момент инерции системы может быть рассчитан по соотношению:
, (16)
где JД – момент инерции ротора двигателя;
–коэффициент, учитывающий момент инерции остальных элементов
электропривода: муфт, тормозного шкива, редуктора и др.;
(17) – приведенный к валу двигателя суммарный момент инерции движущихся исполнительных органов рабочей машины и связанных с ними движущихся масс (грузов, заготовок и т.п.).
В данном проекте допускается рассчитывать момент инерции передачи приближенно, принимая в формуле (16) коэффициент 
= 1.3…1,5
Для учёта влияние упругостей в механизме указана крутильная жесткость СК.
Приведенную к валу двигателя жесткость упругой механической связи СПР
определяют через значение крутильной жесткости рабочего вала (упругой муфты) по формуле:
МН*м/рад (18)
Также в Таблицу 5 записывается установившаяся скорость 
Таблица 5
| Участок движения | Рабочий ход | Обратный ход | |||||||||
| Расчётные данные | Обозначения | Пуск | Уст. Реж. | Тормож. | Пуск | Уст. Реж. | Тормож. | ||||
| По данным Таблицы 2 | |||||||||||
| Скорость РО, м/с | vРО | 0,25 | 0,5 | 0,25 | 0,5 | 0,75 | 0,5 | ||||
| Момент статический РО, кНм | Мрост | 703.627 | 274.586 | ||||||||
| Момент инерции РО, кг·м2 | JРО | 527.5 | 90 | ||||||||
| Приведение к валу двигателя (i=40, КПД=0.97) | |||||||||||
| Скорость двигателя |
| - | 80 | - | - | 120 | - | ||||
| Момент статический на валу | |||||||||||
| без учёта потерь в передаче, Нм | Мпр ( | 17.591 | 6.865 | ||||||||
| с учётом КПД редуктора, Нм | Мвс ( | 18.135 | 6.659 | ||||||||
| с учётом механических потерь, Нм | Мс | 20.47 | 4.323 | ||||||||
| Приведённый момент инерции | Jпр | 0.73 | 0.456 | ||||||||
| Момент инерции электропривода | J | 0.865 | 0.591 | ||||||||
| Динамический момент, Нм | Мдин | 138.35 | 94.6 | ||||||||
| Момент двигателя, допуск. по ускор. | Мдопуск | 45.604 | |||||||||
| Данные предварительного Расчёта | |||||||||||
| Момент двигателя средний на участке, Нм | Мср | 39.743 | |||||||||
| Время работы, с | t | 0.5 | 13.5 | 0.5 | 0.75 | 8.583 | 0.75 | ||||
| Угол поворота вала двигателя, рад/с | α | 20 | 1055 | 45 | 20 | 1055 | 45 | ||||
В таблицу, в строку МДОП.УСК, необходимо включить также требуемые пусковые МП и тормозные МТ моменты двигателя, при которых обеспечивается возможность разгона и торможения электропривода с заданным допустимым ускорением:
(19)
Если момент Мдоп. уск. больше максимального допустимого момента двигателя, то ускорение приходится снижать, что повлечет за собой уменьшение производительности рабочей машины, или выбирать двигатель большей мощности, обеспечивающий требуемое ускорение электропривода.
В данном случае, Мдоп. уск. < Mmax: 45.604 Нм < 155 Нм
studfiles.net
Приближенное значение динамического момента инерции короткозамкнутого ротора:
.
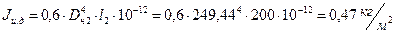Масса изолированных проводов обмотки статора при круглом поперечном сечении:
.
Количество вентиляционных лопаток принимаем равным:
.
Тогда толщина лопатки:
.
Длина лопатки:
.
Высота лопатки:
.
Масса алюминия короткозамкнутого ротора с литой клеткой:
Масса стали сердечника статора и ротора:
Масса изоляции статора при трапецеидальных полузакрытых пазах:
Масса конструкционных материалов двигателя со степенью защиты IP44, станина и щиты из стали или чугуна, ротор короткозамкнутый:
.
Масса двигателя с короткозамкнутым ротором:
Расчет надежности обмотки статора
Расчет надежности всыпных обмоток статора асинхронного двигателя
Дефектность витковой изоляции до начала эксплуатации электродвигателя:
.
Вероятность плотного касания соседних витков:
.
Периметр свободной площади слоя обмотки:
.
Количество проводников, находящихся в наружном слое секции (по периметру секции):
.
Количество элементарных витков в секции:
.
Количество проводников, находящихся во внутреннем слое секции:
.
Доля пар соседних элементарных проводников, принадлежащих одному эффективному:
.
Общая длина пар соседних витков в обмотке:
.
Количество последовательно соединенных секций в фазе:
.
Среднее значение и среднее квадратичное отклонение величин фазных коммутационных перенапряжений на секции:
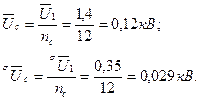
Номинальное фазное напряжение, приходящееся на секцию:
.
Среднее значение напряжения перекрытия по поверхности изоляции промежутка толщиной, равной двусторонней толщине изоляции и среднее квадратичное отклонение его:
Методом экстраполяции находим, что:
.
Двусторонняя толщина провода:
.
Тогда вероятность отказа витковой изоляции при воздействии одного импульса перенапряжения и при условии, что на касающихся витках имеются совпадающие дефекты:
.
Коэффициенты уравнения, определяющие скорость роста дефектности витковой изоляции:
Частота включений электродвигателя:
.
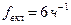Скорость роста дефектности витковой изоляции:
.
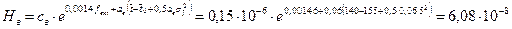Вероятность возникновения КЗ витковой изоляции на длине касающихся витков в течение времени τ:
Вероятность отказа межвитковой изоляции в течение времени τ:
.
Вероятность безотказной работы межвитковой изоляции в течение времени τ:
.
Вероятность безотказной работы обмотки статора в течение времени τ:
.
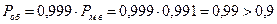Механический расчет вала
Расчет вала на жесткость
Сила тяжести сердечника ротора с обмоткой и участком вала по длине сердечника:
.
Рисунок 23. Эскиз вала к механическому расчету.
Номинальный момент вращения:
.
Валы двигателей с высотами оси вращения 
выполняют с минимальным числом ступеней – 3. Согласно таблице 1-3 [1] определяем по величие наибольшего допускаемого момента длину выступающего конца вала, размеры призматической шпонки и шпоночного паза, связанные с диаметром выступающего цилиндрического конца вала:
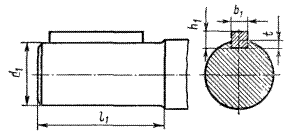
Рисунок 24. Эскиз выступающего конца цилиндрического вала.
Диаметр вала под подшипник и диаметр вала за подшипником принимаем по таб. 3-1 [1]:
Согласно таблице 4.1 [2]
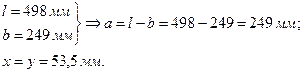
Определим экваториальный момент инерции вала для места посадки сердечника:
Найдем вспомогательные коэффициенты:
Под воздействием силы тяжести прогиб вала посередине сердечника:
.
Соединение с приводимым механизмом осуществляется через упругую муфту МУВП 1-55, которая имеет следующие характеристики:
Поперечная сила, вызываемая передачей через упругую муфту:
.
Прогиб вала посередине сердечника вследствие действия поперечной силы:
Начальный расчетный эксцентриситет сердечника ротора, возникающий вследствие неравномерности воздушного зазора под действие сил тяжести и поперечных равен:
.
Сила одностороннего магнитного притяжения при смещении сердечника на величину расчетного эксцентриситета:
.
Дополнительный прогиб от силы 
:
.
Установившийся прогиб вала:
.
Результирующий прогиб вала:
.
Проверка правильности расчетов:
– условие правильности расчетов истинно.
infopedia.su
.
, откуда 
.
, и 
; 
,
;
.
,
. Они характерны для станочных приводов подачи, вентилей, дросселей и т.д. На рисунке 2.3 изображен нагрузочныймомент вязкого трения, характеризующийся линейной (или близкой к ней) зависимостью величины от скорости - 
, где n = 1,5…2.5.
.
с
=1)
1)
